8.9. Властивості тригонометричних функцій
8.9.1. Парність і непарність тригонометричних функцій
Якщо при повороті навколо точки О на кут![]() початковий радіус ОА переходить у радіус ОВ, то при повороті на кут
початковий радіус ОА переходить у радіус ОВ, то при повороті на кут ![]() початковий радіус ОА перейде у радіус
початковий радіус ОА перейде у радіус ![]() , симетричний ОВ відносно осі абсцис (рис. 16).
, симетричний ОВ відносно осі абсцис (рис. 16).
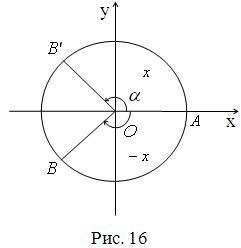
Абсциси точок В і ![]() рівні, а ординати рівні за модулем, але протилежні за знаком. Це означає, що
рівні, а ординати рівні за модулем, але протилежні за знаком. Це означає, що ![]() ,
, ![]() ,
,
![]() ,
, ![]() . Таким чином, функції
. Таким чином, функції ![]() ,
, ![]() ,
, ![]() непарні, а функція
непарні, а функція ![]() парна.
парна.
Приклад 20. Дослідити на парність функції: а) ![]() ;
;
б) 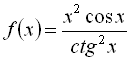 ; в)
; в) ![]() .
.
Розв’язання
а)![]()
![]()
![]()
![]()
![]() функція
функція ![]() є непарною.
є непарною.
б)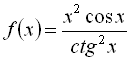
![]()
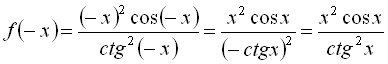
![]()
![]() функція
функція 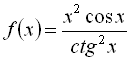 є парною.
є парною.
При дослідженні функції на парність можна скористатися системою Maple, замінивши незалежну змінну х на –х у прикладі в):
> f:=x->sin(2*x)*cos(5*x);
![]()
> f(-x);
![]()
Очевидно, що функція ![]() є непарною.
є непарною.
8.9.2. Періодичність тригонометричних функцій
Для періодичної функції ![]() виконується рівність
виконується рівність ![]() , де Т – відмінне від нуля число, назване періодом функції. Кожна періодична функція має велику кількість періодів, тобто якщо Т – період, то пТ – період, де
, де Т – відмінне від нуля число, назване періодом функції. Кожна періодична функція має велику кількість періодів, тобто якщо Т – період, то пТ – період, де ![]() ,
, ![]() . Звичайно, говорячи про період, мають на увазі найменший додатний період, який називається основним. Основними періодами для тригонометричних функцій є:
. Звичайно, говорячи про період, мають на увазі найменший додатний період, який називається основним. Основними періодами для тригонометричних функцій є: ![]() для функцій
для функцій ![]() ,
, ![]() ;
; ![]() для функцій
для функцій ![]() ,
, ![]() . У більш загальному вигляді можемо записати:
. У більш загальному вигляді можемо записати: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Якщо кути виражаються в радіанах, то ![]() – основний період функцій
– основний період функцій ![]() ,
, ![]() ;
; ![]() – основний період функцій
– основний період функцій ![]() ,
, ![]() .
.
Відомо, що періоди функцій ![]() і
і ![]() обчислюються за формулою
обчислюються за формулою 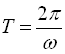 , а періоди функцій
, а періоди функцій ![]() і
і ![]() – за формулою
– за формулою 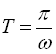 .
.
Якщо період функції ![]() дорівнює
дорівнює ![]() , а період функції
, а період функції ![]() дорівнює
дорівнює ![]() , то період функції
, то період функції ![]() і
і ![]() дорівнює найменшому числу, при діленні якого на
дорівнює найменшому числу, при діленні якого на ![]() і
і ![]() дістаємо цілі числа.
дістаємо цілі числа.
Приклад 21. Знайти період функції: а) 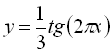 ; б)
; б) ![]() ;
;
в) 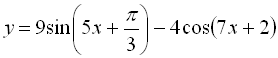 .
.
Розв’язання
а) Період функції 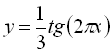 дорівнює
дорівнює 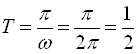 .
.
б) Для того, щоб знайти період функції ![]() , потрібно застосувати формули пониження степеня:
, потрібно застосувати формули пониження степеня: 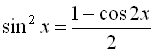 , тобто
, тобто 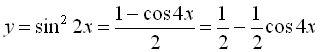 . Період функції
. Період функції 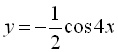 , а отже і даної функції
, а отже і даної функції ![]() є число
є число 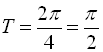 .
.
в) Знаходимо періоди доданків. Період функції 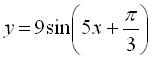 дорівнює
дорівнює 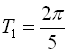 , а період функції
, а період функції ![]() дорівнює
дорівнює 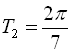 . Очевидно, що період заданої функції дорівнює
. Очевидно, що період заданої функції дорівнює ![]() .
.
8.10. Властивості функцій 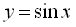 і
і 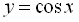 та їх графіки
та їх графіки
Таблиця 5 – Властивості функцій ![]() і
і ![]()

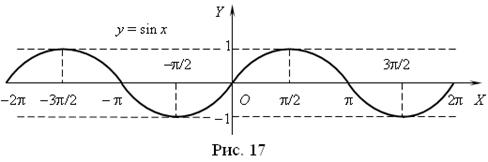
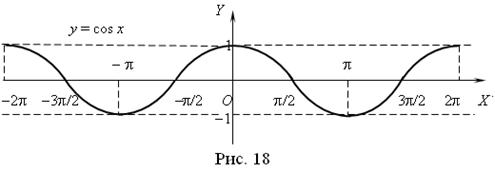
Графік функції ![]() називається синусоїдою (рис. 17), а графік функції
називається синусоїдою (рис. 17), а графік функції ![]() – косинусоїдою (рис. 18).
– косинусоїдою (рис. 18).
8.11. Властивості функцій 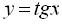 і
і 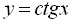 та їх графіки
та їх графіки
Таблиця 6 – Властивості функцій ![]() і
і ![]()
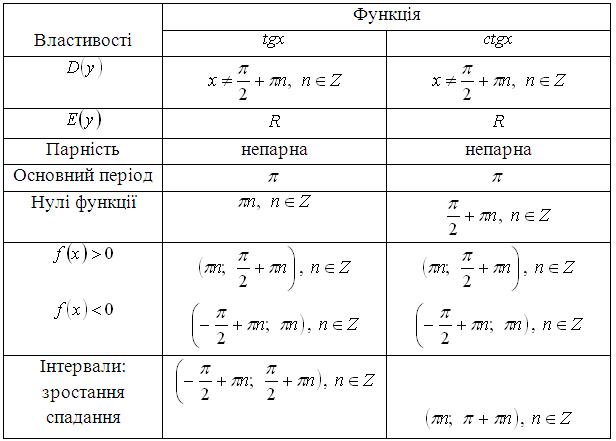
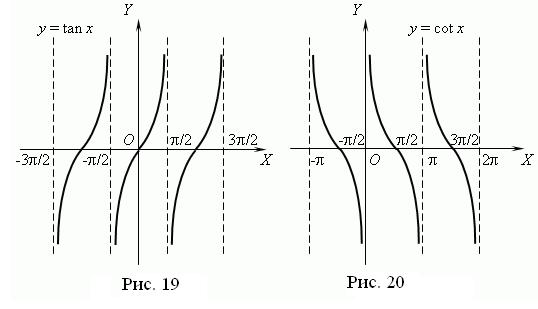
Графік функції ![]() називається тангенсоїдою (рис. 19), а графік функції
називається тангенсоїдою (рис. 19), а графік функції ![]() – котангенсоїдою (рис. 20).
– котангенсоїдою (рис. 20).