8.12. Поняття оборотної та оберненої функцій

Функція, яка приймає кожне своє значення в єдиній точці області визначення, є оборотною.

У такої функції за значенням залежної змінної можна однозначно визначити, якому значенню аргументу воно відповідає.

Інакше кажучи, якщо функція є оборотною й число а належить до її області значень , то рівняння має розв’язок, причому єдиний.

Оберненою до даної оборотної функції називається така функція , яка кожному із множини значень функції ставить у відповідність єдине число x з області визначення.

Функції, обернені функціям , , , на відповідних інтервалах, називаються оберненими тригонометричними. Вони позначаються , , , .

Тригонометричні функції , не є монотонними у всій області їх визначення. Тому для утворення обернених функцій виділяють інтервали монотонності.

8.12.1. Функція 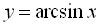та її графік

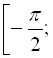
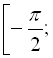
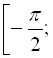
Функція на відрізку зростає і набуває всіх значень з відрізка . Тому функція на відрізку оборотна, тобто має обернену функцію, що називається арксинусом і позначається . Таким чином, арксинусом числа х називається число з відрізка таке, що його синус дорівнює х. Математично це можна записати так: , , .

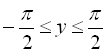Наприклад, 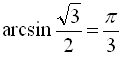(оскільки , ), , , .

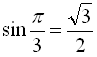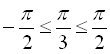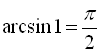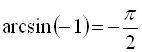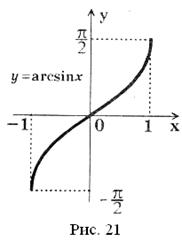
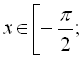
Графік функції , який зображений на рисунку 21, симетричний графіку функції , відносно прямої .

Основні властивості функції

1)  .

2)  .

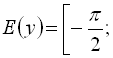
3) , тобто – непарна функція.

4) Функція зростаюча.

5)  при .

8.12.2. Функція 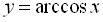та її графік

Функція на відрізку спадає і набуває всіх значень з відрізка . Тому функція на відрізку оборотна, тобто має обернену функцію, що називається арккосинусом і позначається . Таким чином, арккосинусом числа х називається число з відрізка таке, що його косинус дорівнює х. Математично це можна записати так: , , .

Наприклад, 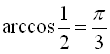(оскільки 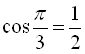, 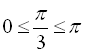), , і т.д.

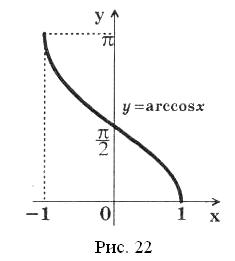
Графік функції  зображено на рисунку 22. Цей графік симетричний графіку функції відносно прямої .

Основні властивості функції

1)  .

2)  .

3) , тобто функція є функцією загального виду.

4) Функція є спадною.

5)  при .

8.12.3. Функція 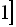та її графік

Функція на інтервалі 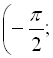зростає і набуває всіх числових значень, оскільки . Тому функція на інтервалі 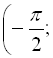оборотна, тобто має обернену функцію, що називається арктангенсом і позначається . Таким чином, арктангенсом числа х називається число з інтервалу 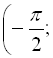таке, що його тангенс дорівнює х. Математично це можна записати так: , , .

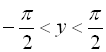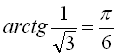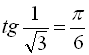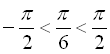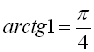Наприклад, (оскільки , ), , , і т.д.

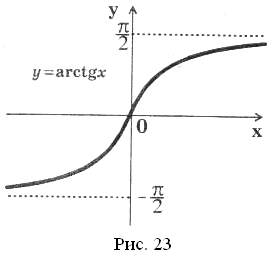
Графік функції 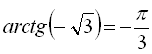зображений на рисунку 23. Цей графік си-

метричний графіку функції , , відносно прямої .

Основні властивості функції

1)  .

2)  .

3) 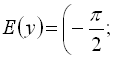, тобто дана функція є непарною.

4) Функція є зростаючою.

5)  при .

8.12.4. Функція 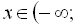та її графік

Функція на інтервалі спадає і набуває усіх числових значень, оскільки . Тому функція на інтервалі оборотна, тобто має обернену функцію, що називається арккотангенсом і позначається . Таким чином, арккотангенсом числа х називається число з інтервалу таке, що його котангенс дорівнює х. Математично це можна записати так: , , .

Наприклад, (оскільки , 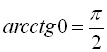), , 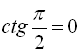, 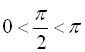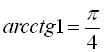і т.д.

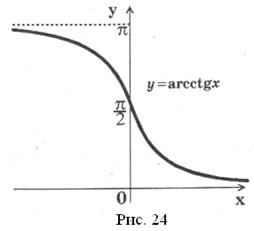
Графік функції 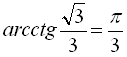зображено на рисунку 24. Цей графік симетричний графіку функції 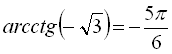відносно прямої .

Основні властивості функції

1)  .

2)  .

3) ,тоб-то дана функція є функцією загального виду.

4) Функція спадна.

5)  при .

Виходячи з означення тригонометричних функцій, запишемо декілька співвідношень між цими функціями:

при , ,

для кутів ,

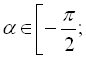для кутів .

Аналогічні співвідношення зв’язують і ; і :

для всіх , ,

для всіх ,

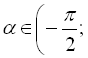для всіх .

Приклад 22. Обчислити:

а) ;

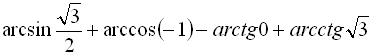б) ; в) ; г) .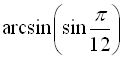

Розв’язання

а) Оскільки 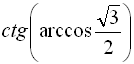, , , , 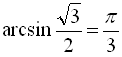то ;

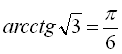
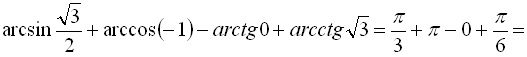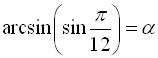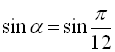б) Позначимо . Оскільки з визначення випливає, що , то .

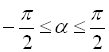
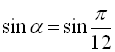Звідси остаточно .

в) .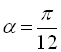

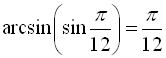
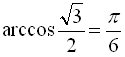г)

.
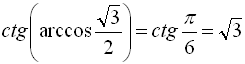
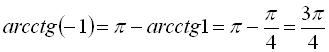