8.13. Приклад перетворень виразів, що містять обернені тригонометричні функції
Приклад 23. Спростити вираз ![]() , де
, де ![]() .
.
Розв’язання
Припустимо, ![]() . Тоді
. Тоді ![]() ,
, ![]() . Треба знайти
. Треба знайти ![]() . Відомо, що
. Відомо, що ![]() ,
, ![]() , а на відрізку
, а на відрізку ![]()
![]() синус набуває лише невід’ємного значення. Тому
синус набуває лише невід’ємного значення. Тому ![]() , тобто
, тобто ![]() .
.
> simplify(sin(arccos(x)));
![]()
Приклад 24. Обчислити 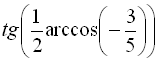 .
.
Розв’язання
Припустимо 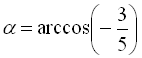 . Тоді
. Тоді 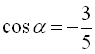 ,
, 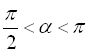 . Треба обчислити
. Треба обчислити ![]() .
.
Маємо 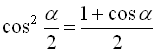 , значить
, значить 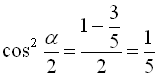 . Оскільки далі
. Оскільки далі 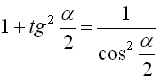 , то
, то 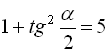 , звідки
, звідки 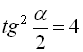 , тобто
, тобто 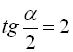 або
або 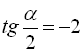 .
.
За умовою 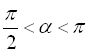 означає
означає 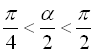 , а в інтервалі
, а в інтервалі ![]()
![]() маємо
маємо 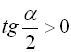 . Отже
. Отже 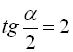 , тобто
, тобто 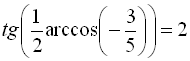 .
.
Відповідь: 2.
Спробуємо спростити вираз 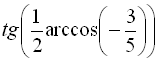 :
:
> simplify(tan(1/2*(arccos(-3/5))));
![]()
Очікуваного результату не дістали. Спробуємо обчислити даний вираз:
> evalf(tan(1/2*(arccos(-3/5))));
![]()
Приклад 25. Обчислити 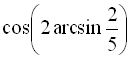 .
.
Розв’язання
Припустимо, 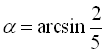 . Тоді
. Тоді 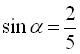 ,
, 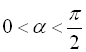 . Потрібно обчис-
. Потрібно обчис-
лити ![]() . Виразимо формулу косинуса подвійного кута через синус кута:
. Виразимо формулу косинуса подвійного кута через синус кута: ![]() . Тоді, підставляючи значення
. Тоді, підставляючи значення ![]() , будемо мати
, будемо мати 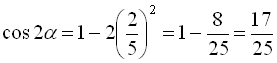 . Отже,
. Отже, 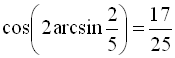 .
.
Відповідь: ![]() .
.
Приклад 26. Обчислити 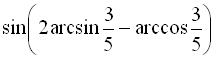 .
.
Розв’язання
Позначимо 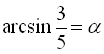 , а
, а 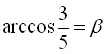 , тоді
, тоді 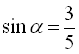 ,
, 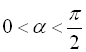 , а
, а
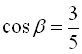 ,
, 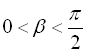 . Потрібно обчислити
. Потрібно обчислити ![]() . Для цього скористаємося формулою (18), отже
. Для цього скористаємося формулою (18), отже
![]() . (*)
. (*)
Згідно з формулою (21) маємо ![]() . Знайдемо
. Знайдемо ![]() :
: ![]() , тобто
, тобто 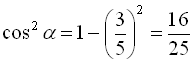 , то
, то 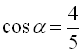 або
або 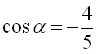 . За умовою
. За умовою 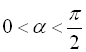 маємо, що
маємо, що ![]() . Тобто
. Тобто 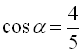 , а отже
, а отже 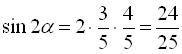 .
.
![]() будемо шукати як у попередньому прикладі, тобто
будемо шукати як у попередньому прикладі, тобто 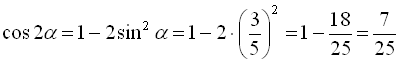 . Значить,
. Значить, 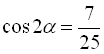 .
.
Знайдемо ![]() з формули
з формули ![]() , підставляючи
, підставляючи 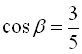 :
: 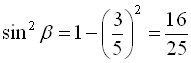 ,
, 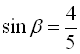 або
або 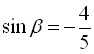 . За умовою
. За умовою 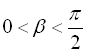 маємо, що
маємо, що ![]() , тобто
, тобто 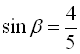 .
.
Знайдені значення підставимо у рівність (*):
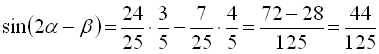 .
.
Відповідь: ![]() .
.
Задамо даний приклад у Maple, а потім smart-способом обчислимо його:
> sin(2*arcsin(3/5)-arccos(3/5));
![]()
> .35199.
Результат система видала наближено у вигляді числа з плаваючою точкою 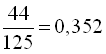 .
.
8.14. Побудова графіків тригонометричних функцій
Приклад 27. Побудувати графік функції ![]() .
.
Розв’язання
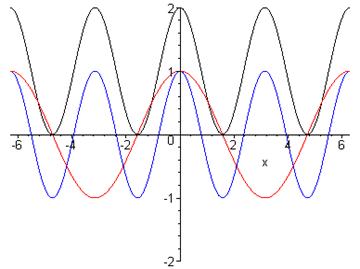
Шляхом елементарних перетворень будуємо графіки таких функцій:
1) ![]() ;
;
2) ![]() (стиснути графік
(стиснути графік ![]() вздовж осі
вздовж осі ![]() до осі
до осі ![]() у 2 рази);
у 2 рази);
3) ![]() (зсунути графік
(зсунути графік![]() вздовж осі
вздовж осі ![]() на 1 одиницю вгору).
на 1 одиницю вгору).
> plot([cos(x),cos(2*x),cos(2*x)+1],x=-2*Pi..2*Pi,-2..2,color=[red,blue,black]);
Приклад 28. Побудувати графік функції 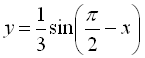 .
.
Розв’язання
І спосіб: Перетворимо 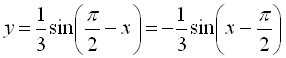 .
.
Шляхом елементарних перетворень будуємо графіки таких функцій:
1) ![]() ;
;
2) 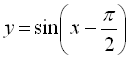 (зсуваємо графік
(зсуваємо графік ![]() на
на ![]() вправо вздовж осі
вправо вздовж осі ![]() );
);
3) 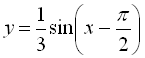 (стискаємо графік
(стискаємо графік 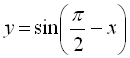 до осі
до осі ![]() у 3 рази);
у 3 рази);
4) 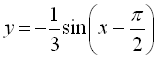 (перевертаємо графік
(перевертаємо графік 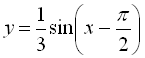 відносно осі
відносно осі ![]() ).
).
> plot([sin(x),sin(x-Pi/2),(1/3)*sin(x-Pi/2),-(1/3)*sin(x-Pi/2)],x=-2*Pi..2*Pi,-2..2,color=[blue, brown,black,red],linestyle=[3,2,0,1],thickness=3);
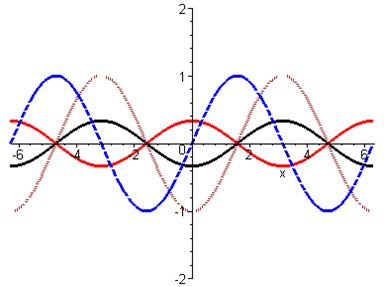
ІІ спосіб: Перетворимо функцію 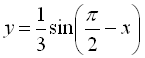 за допомогою фор-
за допомогою фор-
мул зведення: 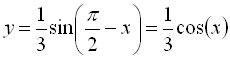 .
.
Переконаємось в Maple, що графіки початкової функції і функції, отриманої за допомогою формул зведення, – ідентичні:
> plot(-(1/3)*sin(x-Pi/2),x=-2*Pi..2*Pi,-2..2);
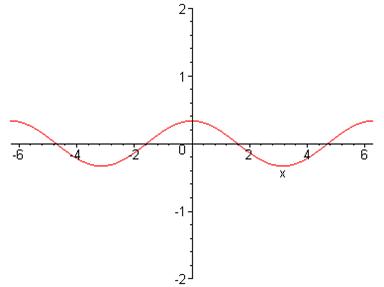
> plot((1/3)*cos(x),x=-2*Pi..2*Pi,-2..2);

Приклад 29. Побудувати графік функції ![]() .
.
Розв’язання
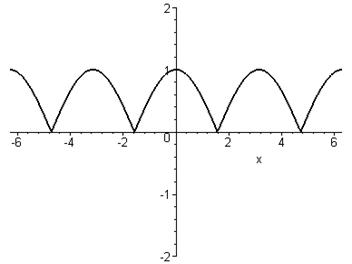
Спочатку будуємо графік функції ![]() . Для того, щоб утворився графік функції
. Для того, щоб утворився графік функції ![]() , потрібно ту частину графіка
, потрібно ту частину графіка ![]() , яка вище осі
, яка вище осі ![]() , залишити без змін, а ту, що нижче осі
, залишити без змін, а ту, що нижче осі ![]() , симетрично відобразити на верхню півплощину.
, симетрично відобразити на верхню півплощину.
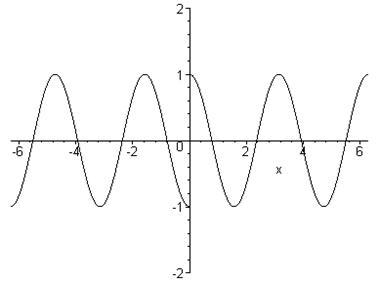
> plot(abs(cos(x)),x=-2*Pi..2*Pi,-2..2,color=black,thickness=2);
Приклад 30. Побудувати графік функції ![]() .
.
Розв’язання
Будуємо графік функції ![]() . Ту частину побудованого графіка, яка в лівій півплощині відносно осі OY, відкидаємо, а ту, що в правій, – залишаємо і симетрично відображаємо на ліву півплощину.
. Ту частину побудованого графіка, яка в лівій півплощині відносно осі OY, відкидаємо, а ту, що в правій, – залишаємо і симетрично відображаємо на ліву півплощину.
> plot(sin(abs(x)),x=-2*Pi..2*Pi,-2..2,color=black);
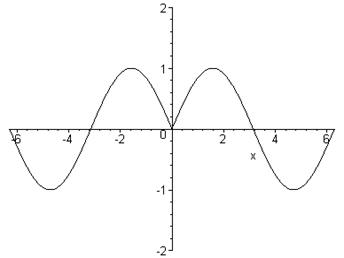
Приклад 31. Побудувати графік функції 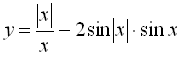 .
.
Розв’язання
![]()
![]()
![]() .
.
Оскільки підмодулевий вираз це х, то розглянемо два випадки:
Якщо ![]() :
: 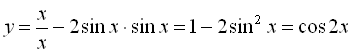 .
.
Якщо ![]() :
: 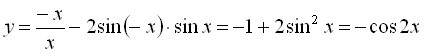 .
.
Шляхом елементарних перетворень будуємо відповідні графіки функцій.
> plot(abs(x)/x-2*sin(abs(x))*sin(x),x=-2*Pi..2*Pi,-2..2,color=black,discont=true);