9. ТРИГОНОМЕТРИЧНІ РІВНЯННЯ
9.1. Найпростіші тригонометричні рівняння
Рівняння називається тригонометричним, якщо невідома величина знаходиться під знаком тригонометричних функцій. Найпростішими тригонометричними рівняннями називаються рівняння 
, 
, 
, 
. Розв’язати найпростіше тригонометричне рівняння – означає знайти множину всіх кутів, що мають дане значення 
тригонометричної функції. Якщо тригонометричне рівняння не є найпростішим, то за допомогою тотожних перетворень його треба звести до одного або кількох найпростіших, розв’язання яких визначається стандартними формулами.
, 
(оскільки 
). Корені рівняння можна розглядати як абсциси точок перетину синусоїди 
з прямою 
.
Всі розв’язки рівняння записуються у вигляді 
, 
. Однак в трьох таких випадках, коли
, розв’язки рівнянь зображуються такими формулами:
при 
, 
;
при 
, ;
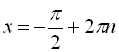при 
, .
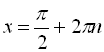Рівняння 
. Оскільки 
, то рівняння має розв’язок тільки при 
. Корені рівняння можна розглядати як абсциси точок перетину косинусоїди 
з прямою .
Всі розв’язки рівняння записуються у вигляді 
, .
Для окремих випадків 
, 
маємо:
а) 
, ;
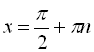б) 
, ;
в) 
, .
Всі корені рівняння 
, 
задаються формулою 
, .
У випадку 
розв’язок записується у вигляді 
, .
Всі корені рівняння 
, 
визначаються співвідношенням 
,. При 
розв’язок має вигляд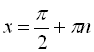 
, 
.
При використанні формул для розв’язування тригонометричних рівнянь враховують, що
; 
;
; 
.
У системі Maple тригонометричні рівняння розв’язуються за допомогою вищезгаданої функції solve. До тих пір, поки не буде набрано _EnvAllSolutions:=true, вбудована функція solve повертає користувачу лише один або декілька коренів з множини розв’язків тригонометричного рівняння. Після даної команди система повертає всю множину коренів для кожного тригонометричного рівняння.
Розглянемо на прикладах найпростіші тригонометричні рівняння.
Приклад 1. Розв’язати рівняння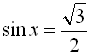 
.
Розв’язання
Оскільки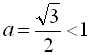 
, то скористаємось формулою , . Отже,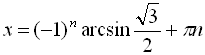 
, 
, .
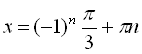Відповідь: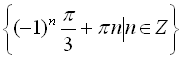 
.
> solve(sin(x)=sqrt(3)/2);
> _EnvAllSolutions:=true:solve(sin(x)=sqrt(3)/2);
Форма відповіді незвичайна, але корені знайдені правильно. Система Maple через _В, незалежно від індексу, позначає змінні, що приймають значення з множини 
, а через _Z - множину цілих чисел.
Приклад 2. Розв’язати рівняння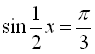 
.
Розв’язання
(
), отже, рівняння розв’язків не має.
Відповідь: 
.
> _EnvAllSolutions:=true:solve(sin((1/2)*x)=Pi/3,x);
Оскільки
> evalf(arcsin(1/3*Pi));
очевидно, що всі розв’язки містять уявну одиницю 
, тобто ці корені комплексні і у відповідь не входять.
Спробуємо знайти розв’язок даного рівняння після підключення пакета with( RealDomain):
> restart;
> with( RealDomain):
solve(sin((1/2)*x)=Pi/3,x);
Warning, these protected names have been redefined and unprotected: Im, Re, ^, arccos, arccosh, arccot, arccoth, arccsc, arccsch, arcsec, arcsech, arcsin, arcsinh, arctan, arctanh, cos, cosh, cot, coth, csc, csch, eval, exp, expand, limit, ln, log, sec, sech, signum, simplify, sin, sinh, solve, sqrt, surd, tan, tanh
Для функції 
. Тому розв’язок, який знайшла система Maple, – комплексний. А дійсних коренів дане рівняння не має.
Приклад 3. Розв’язати рівняння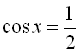 
.
Розв’язання
, 
, 
.
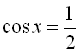
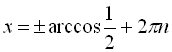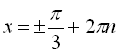Відповідь: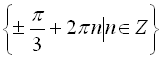 
.
> _EnvAllSolutions:=true:solve(cos(x)=1/2,x);
Отримали ту саму відповідь, записану в іншій формі!
Приклад 4. Розв’язати рівняння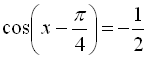 
.
Розв’язання
, 
, 
, 
, 
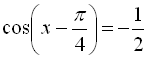
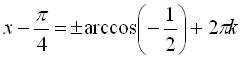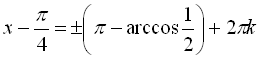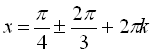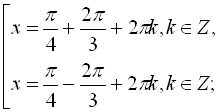
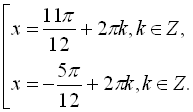
Відповідь: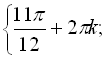 
.
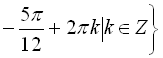Приклад 5. Розв’язати рівняння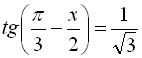 
.
Розв’язання
Запишемо дане рівняння у вигляді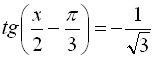 
, тоді скористаємось формулою , , тобто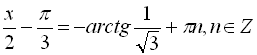 
.
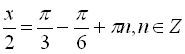
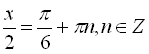
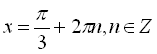Розглянемо ліву і праву частину даного рівняння як окремі функції, і побудуємо графіки цих функцій в системі Maple:
> plot([tan(Pi/3-x/2),1/(sqrt(3))],x=-8..8,-8..8,discont=true);
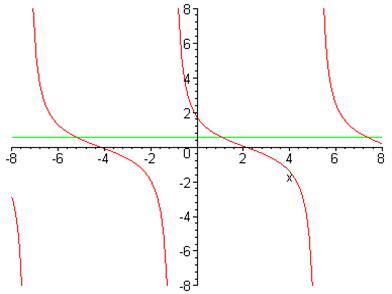
Абсциси точок перетину цих двох графіків і будуть розв’язками рівняння, що розглядається.
Відповідь: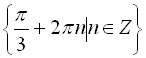 
.
Приклад 6. Розв’язати рівняння 
.
Розв’язання
Оскільки для рівняння , , то
.
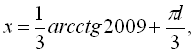
Відповідь: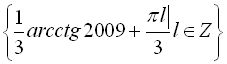 
.
> _EnvAllSolutions:=true:solve(cot(3*x)=2009);
> evalf(%);
Приклад 7. Розв’язати рівняння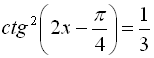 
.
Розв’язання
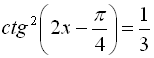
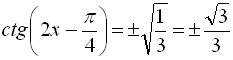
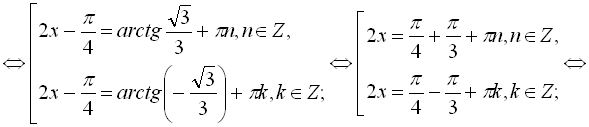
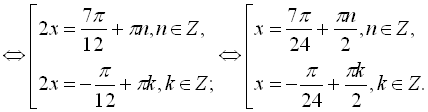
Відповідь: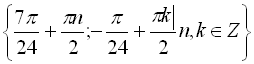 
.
> solve((cot(2*x-Pi/4))^2=1/3);
Розв’язок, отриманий в Maple, відповідає тому, що ми отримали вручну, записаному в іншому вигляді.
Відзначимо, що при 
, 
загальними формулами для тригонометричних рівнянь також можна користуватися, вони дають правильний результат, однак найчастіше ці формули не мають компактного вигляду. Наприклад, якщо використовувати окремі випадки, то 
, 
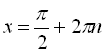. Якщо ж скористатися спільною формулою, то 
, 
. Покажемо, що 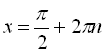, і 
, 
– це та сама множина.
Дійсно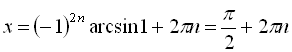, при 
, ; при 
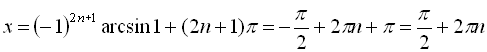, . Таким чином, множини розв’язків, отримані двома способами, збігаються.
Зауваження. При розв’язуванні тригонометричних рівнянь з однаковим успіхом можна користуватися і радіанною, і градусною мірами. Так, наприклад, відповідь у прикладі № 5, яка записана за допомогою радіанної міри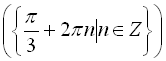 
, можна записати, використовуючи градусну міру, так: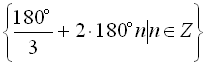 
. При цьому слід знати, що можна використовувати або тільки радіанну, або тільки градусну міру, тобто не можна використовувати в тому самому розв’язку частково радіанну і частково градусну міру.
Приклад 8. Вказати найменший додатний розв’язок рівняння (у градусах):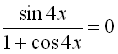 
.
Розв’язання
Дане рівняння є дробово-раціональним, тому його можна записати у вигляді системи: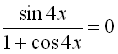 
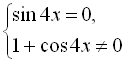
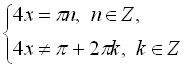
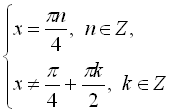. Звідси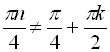 
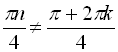
, тобто підходить лише 
. Таким чином,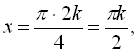 
.
Найменший додатний розв’язок рівняння при 
буде 
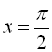або 
.
Відповідь: 
.
При застосуванні Maple до розв’язування тригонометричних рівнянь потрібно бути уважним, оскільки система нерідко видає неправильні відповіді:
> restart:
`Рівняння_8`:=sin(4*x)/(1+cos(4*x))=0;
_EnvAllSolutions:=true:
solve(`Рівняння_8`);`Розв_к_8`:=%:
Для виведення результатів розв’язання рівнянь система генерує сталі. Позначення всіх таких сталих починається знаком «_» – нижнє підкреслення. Знак «~», як відомо, в позначенні змінної вказує, що на її можливі значення накладено певні умови. Для того, щоб взнати більше про конкретну змінну, застосуємо команду:
> about(_Z1);
Originally _Z1, renamed _Z1~:
is assumed to be: integer
Із отриманого повідомлення дізнаємось, що _Z1 може приймати тільки цілі значення. Це означає, що система видала неправильний результат, оскільки насправді _Z1 може приймати тільки парні значення. Але далі – більше. Підставимо отриманий розв’язок у вихідне рівняння та спростимо отриманий вираз:
> subs(x=`Розв_к_8`,`Рівняння_8`);
simplify(%);
І на цьому етапі система не змогла виявити своєї помилки, адже для всіх непарних значень знаменник лівої частини рівняння дорівнює нулю. Але система цього «не побачила» і «вирішила», що знайдений розв’язок задовольняє рівняння. І тільки при спробі підставити замість _Z1 конкретне непарне значення, система нарешті реагує адекватно, повідомляючи про неможливість здійснення операції ділення на нуль:
> simplify(%%) assuming _Z1=1;
Error, (in assuming) when calling `one of {simplify, sin, cos}`. Received: 'numeric exception: division by zero'
В подібних ситуаціях можна спробувати перетворити вихідне рівняння. Наприклад
> convert(lhs(`Рівняння_8`),sincos); expand(lhs(`Рівняння_8`));normal(%);
solve(%);
> about(_Z2);about(_Z3);
Originally _Z2, renamed _Z2~:
is assumed to be: integer
Originally _Z3, renamed _Z3~:
is assumed to be: integer
Ми отримали правильну відповідь, але в незручному вигляді. Головною перепоною на шляху здійснення подібних перетворень є складність формулювання загальних правил з рекомендаціями які саме перетворення вихідних рівнянь потрібно робити у різних випадках.
На думку авторів, надзвичайно ефективний прийом застосування Maple при знаходженні розв’язків тригонометричних рівнянь полягає в наочній перевірці правильності знайдених виразів. Продемонструємо цей прийом. На основі неправильного розв’язку, знайденого системою, згенеруємо координати декількох точок, абсциси яких збігаються зі значеннями кореня:
> `xy_8`:=seq([evalf(eval(`Розв_к_8`,_Z1=k)),0],k=-10..10);
Відповідний діапазон значень 
потрібно підбирати в кожному конкретному випадку. Побудуємо графік лівої частини тригонометричного рівняння, в якому права частина дорівнює нулю
> plot(lhs(`Рівняння_8`)-rhs(`Рівняння_8`),x=-10..10,-10..10,style=[line],symbol=circle,symbolsize=17,color=black,scaling=unconstrained,discont=true);g10:=%:
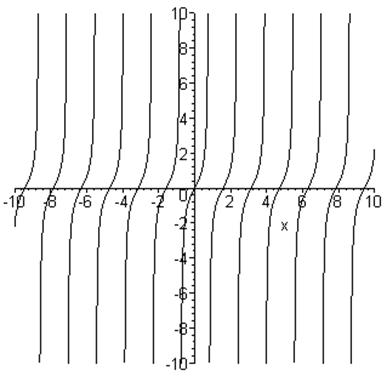
Побудуємо графік, на якому відображено згенеровані точки
> plot([`xy_8`],x=-10..10,-1..1,style=[point],symbol=circle,symbolsize=17,color=red,scaling=unconstrained);g20:=%:
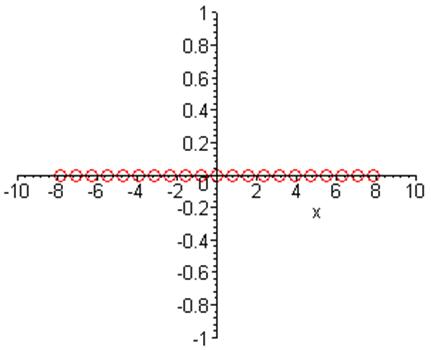
Сумістимо останні два графіки в один
> plots[display]([g10,g20]);
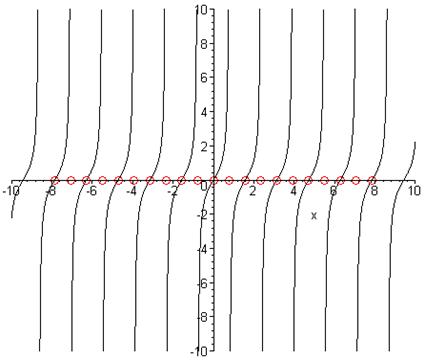
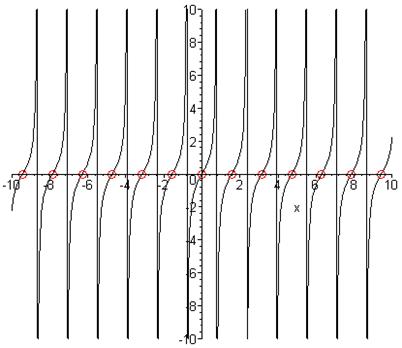
Із графіка видно, що ми маємо «зайві» корені! Зайві корені зображають ті виділені кружечками точки на осі абсцис, через які не проходять криві. Аналогічним чином перевіримо розв’язок, знайдений «вручну»:
> printf(`Згенеруємо координати точок`);
`Корені_вручну_8`:=seq([evalf(Pi*k/2),0],k=-10..10);
printf(`Будуємо графік`);
plot([`Корені_вручну_8`],x=-10..10,-1..1,style=[point],symbol=circle,symbolsize=17,color=red,scaling=unconstrained):g30:=%:
plots[display]([g10,g30]);
Згенеруємо координати точок
Будуємо графік
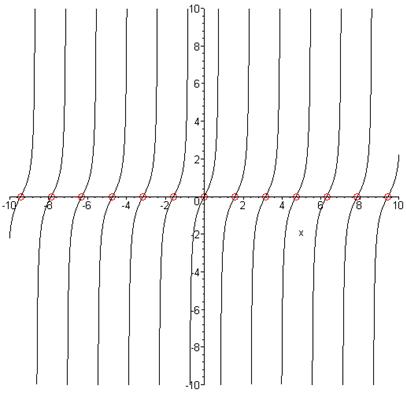
Як видно, в даному випадку – корені правильні.
Декілька слів потрібно сказати про методику виведення графіків в даному випадку. Для суміщення різних графіків в одному ми використали команду plots[display] (команду display пакета plots). Звичайний, більш простий прийом суміщення графіків декількох функцій на одному за допомогою списку функцій в даному випадку неможливий через незрозумілий для авторів конфлікт між побудовою списку точок та опцією discont=true, яка задається для побудови функцій, що мають розриви. Дійсно
> plot([lhs(`Рівняння_8`)-rhs(`Рівняння_8`),[[`Корені_вручну_8`]]],x=-10..10,-10..10,style=[line],symbol=circle,symbolsize=17,color=black,scaling=unconstrained,discont=true);
Error, (in plot) invalid plot function: [[[-15.70796327, 0], [-14.13716694, 0], [-12.56637062, 0], [-10.99557429, 0], [-9.424777962, 0], [-7.853981635, 0], [-6.283185308, 0], [-4.712388981, 0], [-3.141592654, 0], [-1.570796327, 0], [0., 0], [1.570796327, 0], [3.141592654, 0], [4.712388981, 0], [6.283185308, 0], [7.853981635, 0], [9.424777962, 0], [10....
Без задання опції discont=true спосіб суміщення графіків декількох функцій на одному за допомогою списку функцій працює, але графік без указаної опції має дещо інший вигляд:
> plot([lhs(`Рівняння_8`)-rhs(`Рівняння_8`),[`Корені_вручну_8`]],x=-10..10,-10..10,style=[line,point],symbol=circle,symbolsize=17,color=[black,red],scaling=unconstrained);
