9.2. Загальний принцип розв’язування тригонометричних рівнянь
Цей принцип полягає в тому, що всі тригонометричні функції, які входять в рівняння, виражають через яку-небудь одну тригонометричну функцію, яка залежить від одного і того ж аргументу. Розглянемо даний принцип на прикладах:
Приклад 9. Розв’язати рівняння ![]() .
.
Розв’язання
Замінивши ![]() на
на ![]() ,
отримаємо
,
отримаємо ![]()
![]()
![]()
![]() .
Замінимо
.
Замінимо ![]() через
через ![]() :
: ![]()
![]()
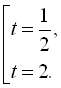
Повертаючись до заміни, отримаємо 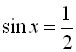 або
або ![]() .
Перше
.
Перше
рівняння системи є найпростішим тригонометричним і його розв’язком буде 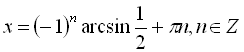
![]()
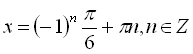 .
У другому рівнянні системи права його частина
.
У другому рівнянні системи права його частина ![]() ,
тому рівняння
,
тому рівняння ![]() розв’язків не має.
розв’язків не має.
Відповідь: 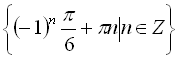 .
.
> _EnvAllSolutions:=true:solve(2*(cos(x))^2+5*sin(x)-4=0);
![]()
Перша і друга серії розв’язків містять уявну одиницю, а третю і четверту
серії розв’язків, тобто 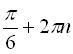 ,
, 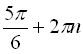 ,
можна записати у звичному вигляді
,
можна записати у звичному вигляді 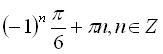 .
.
Приклад 10. Розв’язати рівняння 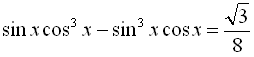 .
.
Розв’язання
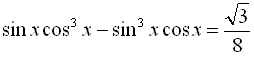
![]()
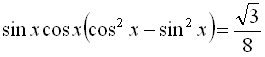
![]()
![]()
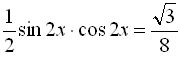
![]()
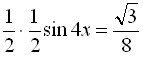
![]()
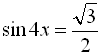
![]()
![]()
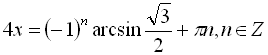
![]()
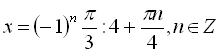
![]()
![]()
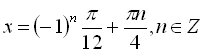 .
.
Відповідь: 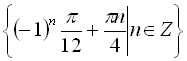 .
.
> solve(sin(x)*(cos(x))^3-((sin(x))^3)*cos(x)=(sqrt(3))/8);
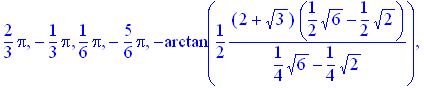
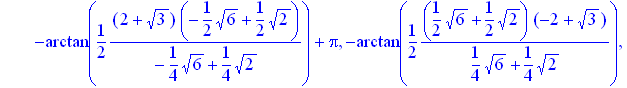
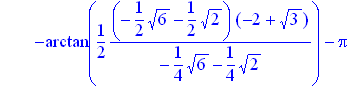
Результат, який видала нам система, навіть без застосування _EnvAllSolutions:=true є досить громістким. Він потребує деякого спрощення. Для того, щоб не спрощувати кожний із елементів списку, можна скористатися командою map(), яка дозволяє застосувати функцію, оператор або команду, задану першим параметром до всіх елементів списку або множини. Робиться це таким чином:
> solve(sin(x)*(cos(x))^3-((sin(x))^3)*cos(x)=(sqrt(3))/8);

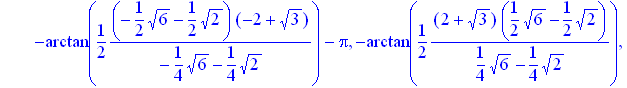
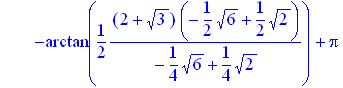
> map(z->simplify(z),[%]);
![]()
9.3. Розв’язування тригонометричних рівнянь методом групування
Шляхом групування доданків рівняння зводяться до вигляду, коли ліва частина розкладена на множники, а права рівна нулю.
Приклад 11. Розв’язати рівняння
![]() .
.
Розв’язання
Згрупуємо доданки в лівій і правій частинах рівняння: ![]() .
За формулою перетворення суми синусів, а також за формулою косинуса подвійного
кута, отримаємо
.
За формулою перетворення суми синусів, а також за формулою косинуса подвійного
кута, отримаємо ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
Звідси
.
Звідси 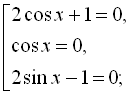
![]()
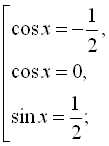
![]()
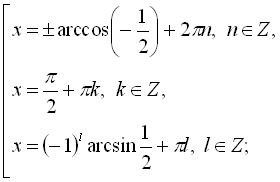
![]()
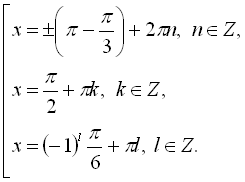
Відповідь: 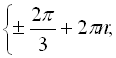
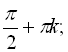
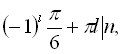
![]()
![]() .
.
> _EnvAllSolutions:=true:
> solve(sin(x)+sin(2*x)+sin(3*x)=1+cos(x)+cos(2*x));
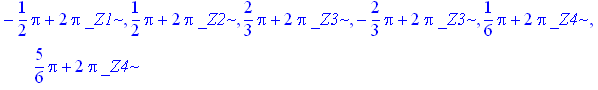
Приклад 12. Розв’язати рівняння 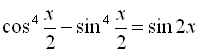 .
.
Розв’язання
За формулою різниці квадратів розпишемо ліву частину рівняння 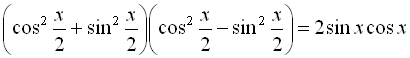
![]()
![]()
![]()
![]()
![]()
![]()
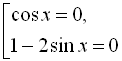
![]()
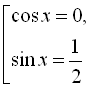
![]()
![]()
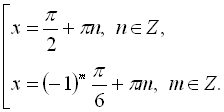
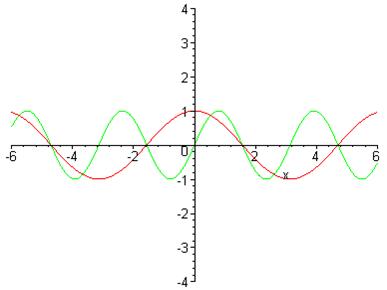
> plot([cos(x/2)^4-sin(x/2)^4,sin(2*x)],x=-6..6,-4..4);
Відповідь: 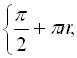
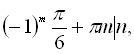
![]() .
.


