9.4. Рівняння, які розв’язуються пониженням степеня
Якщо тригонометричні рівняння містять ![]() ,
, ![]() в парному степені, то застосовують формули пониження степеня
в парному степені, то застосовують формули пониження степеня  ,
, 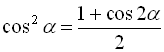 .
.
Приклад 13. Розв’язати рівняння ![]() .
.
Розв’язання
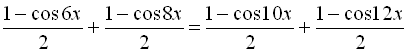
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Кожний множник отриманого рівняння прирівнюємо до нуля і знаходимо його корені: ![]()
![]()
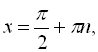
![]() ;
; ![]()
![]()
![]()
![]()
![]()
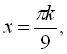
![]()
![]()
![]()
![]()
![]()
![]()
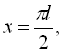
![]() .
.
Відповідь: 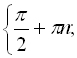
![]()
![]()
![]()
![]() .
.
9.5. Розв’язування однорідних тригонометричних рівнянь, а також рівнянь, які зводяться до однорідних тригонометричних
Однорідні тригонометричні рівняння – це рівняння виду
![]() (1)
(1)
і ![]() . (2)
. (2)
Розв’язуються вони шляхом ділення обох частин рівняння на ![]() для рівняння виду (1) і на
для рівняння виду (1) і на ![]() для рівняння виду (2).
для рівняння виду (2).
Приклад 14. Розв’язати рівняння ![]() .
.
Розв’язання
Поділимо обидві частини рівняння на ![]()

![]() :
:
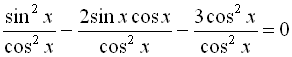
![]()
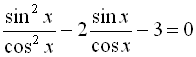
![]()
![]()
![]()
![]()
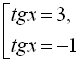
![]()
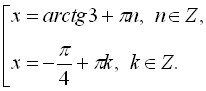
Перевіримо, чи 
![]() не є коренем початкового рівняння:
не є коренем початкового рівняння: 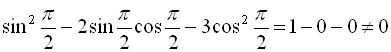 . Отже
. Отже 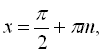
![]() не є коренем нашого рівняння.
не є коренем нашого рівняння.
Відповідь: ![]()

![]() .
.
> solve((sin(x))^2-2*sin(x)*cos(x)-3*(cos(x))^2);
![]()
Приклад 15. Розв’язати рівняння ![]() .
.
Розв’язання
![]()
![]()
![]()
![]()
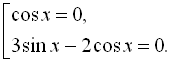
Розв’яжемо перше рівняння сукупності: ![]()
![]()

![]() .
.
Друге рівняння сукупності є однорідним тригонометричним, тому поділимо обидві частини рівняння ![]() на
на ![]() :
: 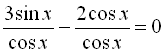
![]()
![]()
![]()
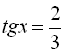
![]()
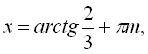
![]() .
.
Оскільки права частина рівняння дорівнює нулю, а ліву частину розглянути як функцію, то графічно розв’язками рівняння будуть абсциси точок перетину графіка функції ![]() з віссю ОХ.
з віссю ОХ.
> plot(3*sin(x)*cos(x)-2*(cos(x))^2,x=-6..6,-4..2);
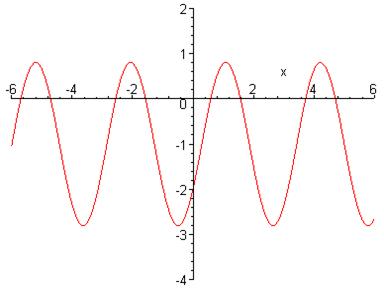
Відповідь: 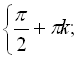
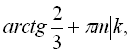
![]() .
.
9.6. Розв’язування тригонометричних рівнянь за допомогою універсальної підстановки 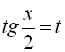
При розв’язуванні рівнянь виду ![]() зручно застосову-вати універсальну підстановку
зручно застосову-вати універсальну підстановку 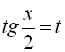 . Тоді функції
. Тоді функції ![]() ,
, ![]() нескладно виражаються через
нескладно виражаються через 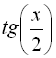 за такими формулами:
за такими формулами:
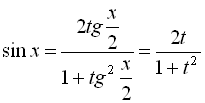 ,
,  .
.
Оскільки використання універсальної підстановки можливе лише при ![]()
![]() , то потрібно перевіряти, чи не є числа виду
, то потрібно перевіряти, чи не є числа виду ![]()
![]() розв’язками початкового рівняння.
розв’язками початкового рівняння.
Приклад 16. Розв’язати рівняння ![]() .
.
Розв’язання
Зробимо підстановку 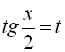 ,
, 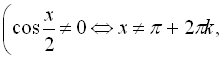
![]() .
.
Тоді 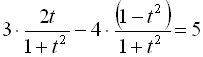
![]()

![]()
![]()
![]()
![]() .
.
Значить 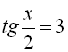
![]()
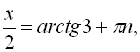
![]()
![]()
![]()
![]() .
.
Перевіримо, чи не є розв’язком даного рівняння ![]()
![]() :
: ![]() .
.
Відповідь: ![]() .
.
Приклад 17. Розв’язати рівняння ![]() .
.
Розв’язання
Можна замінити ![]() через х, а потім зробити підстановку
через х, а потім зробити підстановку 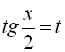 ,
,  . Тоді
. Тоді 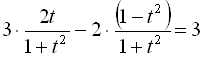
![]()
![]()
![]()
![]() або
або ![]() . Повернувшись до підстановки
. Повернувшись до підстановки  (а) або
(а) або  (б), розв’яжемо по черзі рівняння (а) і (б):
(б), розв’яжемо по черзі рівняння (а) і (б):
(а): 
![]()
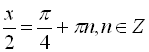
![]()
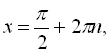
![]()
![]()

![]()
![]()

![]() ;
;
(б): 
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
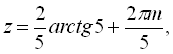
![]() .
.
Перевіримо, чи не є розв’язком даного рівняння ![]()
![]() :
: ![]() .
.
Відповідь: 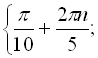
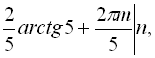
![]() .
.
> solve(3*sin(5*z)-2*cos(5*z)=3,z);
![]()
Бачимо, що перша множина розв’язків ідентична тій, яку ми отримали, розв’язуючи дане рівняння вручну. Друга ж записана в іншому вигляді. Тому перевіримо, чи будуть числа множини 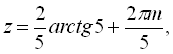
![]() розв’язком нашого рівняння:
розв’язком нашого рівняння:
> j:=3*sin(5*z)-2*cos(5*z)=3;
![]()
> eval(j,z=(2/5)*arctan(5)+2*Pi/5);
![]()
> evalf(%);
![]()
А також перевіримо, чи розв’язок, виданий системою, буде правильним:
> eval(j,z=-(1/5)*arctan(5/12)+Pi/5+2*Pi/5);
![]()
Робимо висновок, що і перший, і другий розв’язки є розв’язками нашого рівняння.


