9.7. Метод введення допоміжного кута
Іноді при розв’язуванні тригонометричних рівнянь корисно скористатися формулою ![]() , де
, де 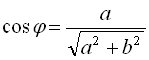 ,
, 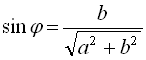 . У цьому випадку
. У цьому випадку ![]() називається допоміжним аргументом або допоміжним кутом.
називається допоміжним аргументом або допоміжним кутом.
Сенс методу полягає в тому, що деяку величину подають як тригонометричну функцію відповідного аргументу ![]() , а потім роблять тригонометричні перетворення.
, а потім роблять тригонометричні перетворення.
Приклад 18. Розв’язати рівняння 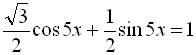 .
.
Розв’язання
1-й спосіб:
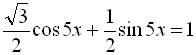
![]()
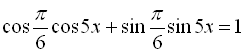
![]()
![]()
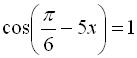
![]()
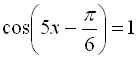
![]()
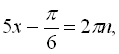
![]()
![]()
![]()
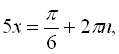
![]()
![]()
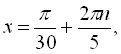
![]() .
.
У процесі розв’язування ми врахували той факт, що якщо 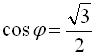 ,
, 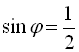 , то
, то ![]() можна покласти таким, що дорівнює
можна покласти таким, що дорівнює ![]() .
.
2-й спосіб:
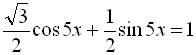
![]()
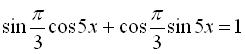
![]()
![]()
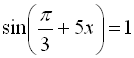
![]()
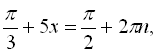
![]()
![]()
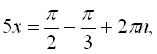
![]()
![]()
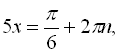
![]()
![]()
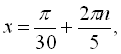
![]() .
.
Відповідь: 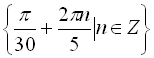 .
.
Приклад 19. Розв’язати рівняння ![]() .
.
Розв’язання
Оскільки ![]() , то поділимо обидві частини нашого рівняння на 2 і введемо допоміжний кут:
, то поділимо обидві частини нашого рівняння на 2 і введемо допоміжний кут: 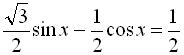
![]()
![]()
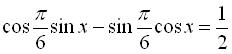
![]()
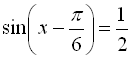
![]()
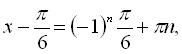
![]()
![]()
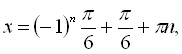
![]() . Даний розв’язок можна розписати як
. Даний розв’язок можна розписати як 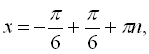
![]()
![]()
![]()
![]() , якщо п – непарне або
, якщо п – непарне або 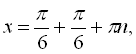
![]()
![]()
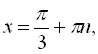
![]() , якщо п – парне.
, якщо п – парне.
Відповідь: 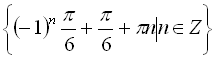 .
.
Розв’яжемо приклад 19 в системі Maple, застосовуючи smart-спосіб для розв’язування рівнянь:
> sqrt(3)*sin(x)-cos(x)=1;
![]()
> R0 := solve({sqrt(3)*sin(x)-cos(x) = 1});
![]()
Як бачимо, одержані в системі Maple розв’язки, є сукупностями коренів, які були отримані при непарному та парному п.
9.8. Розв’язування тригонометричних рівнянь способом підстановки
У деяких раніше розглянутих рівняннях застосовувалася заміна змінної, коли ці рівняння зводилися до алгебраїчних відносно однієї з тригонометричних функцій. Розглянемо більш складні випадки заміни змінних.
Приклад 20. Розв’язати рівняння 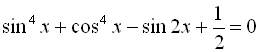 .
.
Розв’язання
Скористаємося формулою ![]() , тоді
, тоді 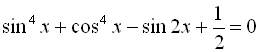
![]()
![]()
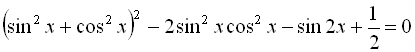
![]()
![]()
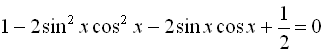
![]()
![]()
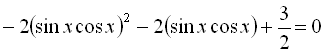 . Зробимо заміну
. Зробимо заміну ![]() :
:
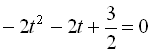
![]()
![]()
![]()
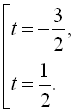 Повернемось до заміни:
Повернемось до заміни:
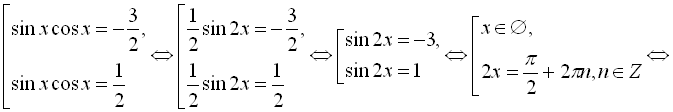
![]()
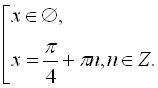
Відповідь: 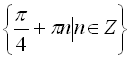 .
.
Приклад 21. Розв’язати рівняння ![]() .
.
Розв’язання
Позначивши ![]() , дістанемо
, дістанемо ![]()
![]()
![]()
![]() . Тоді початкове рівняння запишеться у вигляді
. Тоді початкове рівняння запишеться у вигляді ![]()
![]()
![]()
![]()
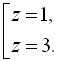 Повернемось до заміни:
Повернемось до заміни:
![]() (1)
(1)
або ![]() . (2)
. (2)
Найпростішим методом розв’язування рівняння (1) є метод введення допоміжного кута:
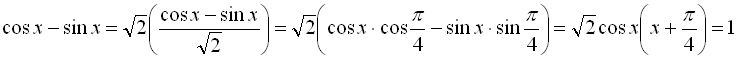
![]()
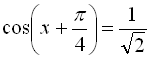
![]()
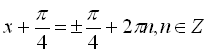
![]()
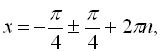
![]() .
.
Друге рівняння сукупності (2) розв’язків не має, оскільки 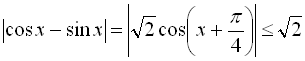 , а число
, а число ![]() .
.
Відповідь: 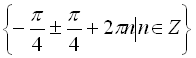 .
.
> solve(4-4*(cos(x)-sin(x))-sin(2*x)=0,x);
![]()
Перші дві серії коренів відповідають розв’язку, отриманому «вручну», останні дві містять уявну одиницю, тому ними можна знехтувати.


