Розв’язування тригонометричних рівнянь із застосуванням комбінованих способів

9.9. Розв’язування тригонометричних рівнянь із застосуванням комбінованих способів

Приклад 22. Розв’язати рівняння .

Розв’язання

Наведемо дві форми запису розв’язання вихідного рівняння.

І форма запису розв’язання.

ОДЗ: .

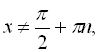
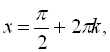
Знаходимо значення х, що задовольняють рівняння і ; якщо ; якщо .

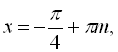
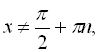
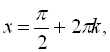
Оскільки через ОДЗ , то серія розв’язків непридатна, вона не входить в ОДЗ, і, відповідно, є лише друга серія розв’язків .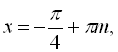

Відповідь: .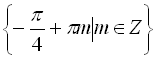

ІІ форма запису розв’язання.

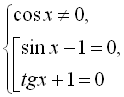
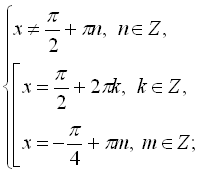
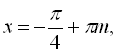
Відповідь: .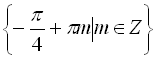

> solve((sin(x)-1)*(tan(x)+1)=0);

З двох отриманих секцій розв’язків випливає розв’язок, виданий у першій секції.

Приклад 23. Розв’язати рівняння 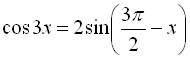. У відповіді зазначте кількість розв’язків на проміжку .

Розв’язання

Скористаємось формулами зведення для правої частини рівняння.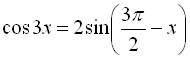

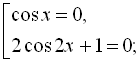
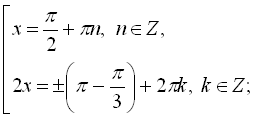
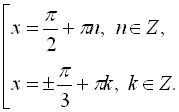
Для ; . Отже розв’язків на відрізку два.

Відповідь: 2.

Приклад 24. Розв’язати рівняння .

Розв’язання

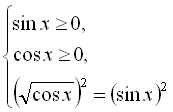Перші дві тригонометричні нерівності нашої комбінованої системи розв’язуємо з урахуванням властивостей тригонометричних функцій. Тоді маємо: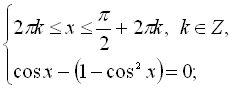

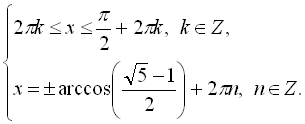
, оскільки друга серія розв’язків зі знаком «–» не задовольняє нерівність .

Відповідь: .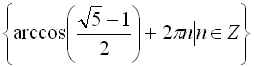

> `Рівняння_24`:=sqrt(cos(x))=sin(x);

Перевіримо правильність знайдених коренів. Для цього згенеруємо координати деякої сукупності точок, абсциси яких збігаються зі значеннями кореня:

> `Корені_24`:=arccos((sqrt(5)-1)/2)+2*Pi*k;

`xy_24`:=seq([evalf(`Корені_24`),0],k=-10..10);

Побудуємо графік

> plot([[`xy_24`],lhs(`Рівняння_24`)-rhs(`Рівняння_24`)],x=-40..40,style=[point,line], symbol=circle,symbolsize=17,scaling=unconstrained);

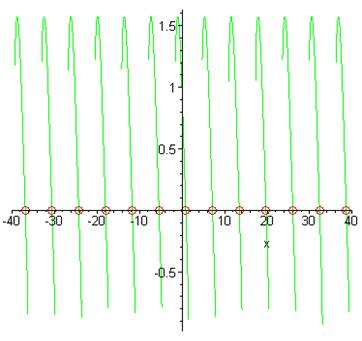
Із графіка видно, що корені знайдені правильно.

Приклад 25. Розв’язати рівняння .

Розв’язання

Оскільки , , то

. Знак «=» з урахуванням наведених нерівностей може мати місце тільки у тому випадку, коли

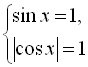
(оскільки ).

Відповідь:.

> `Рівняння_25`:=3*sin(x)^7+5*cos(x)^16=8;

Перенесемо праву частину рівняння в ліву і побудуємо графік виразу

> 3*sin(x)^7+5*cos(x)^16-8;

> plot([lhs(`Рівняння_25`)-rhs(`Рівняння_25`)],x=-40..40,-12..1,style=[line],symbol=circle,symbolsize=17, scaling=unconstrained);

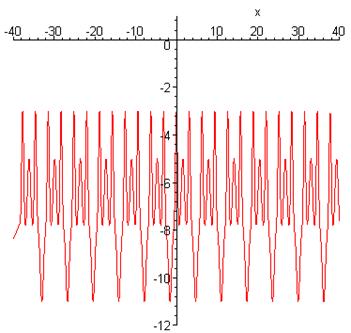
Із графіка видно, що точок перетину з віссю абсцис не існує, отже відповідь правильна.

9.10. Розв’язування тригонометричних рівнянь з параметрами та завдань із застосуванням тригонометричних функцій підвищеної складності

Приклад 26. Визначити кількість цілих значень параметра а, при яких рівняння має розв’язки.

Розв’язання

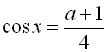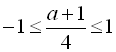
. За властивістю функції – , тому . Цілими значеннями, які належать отриманому проміжку, є: –5; –4; –3; –2; –1; 0; 1; 2; 3. Їх кількість – 9.

Відповідь: 9.

Побудуємо графік прямої , горизонтальних прямих і та отриманих цілочислових значень параметра а.

> plot([[seq([k,0],k=-5..3)],(a+1)/4,-1,1],a=-6..6,-1.2..1.2,style=[point,line$3],symbol=circle,symbolsize=17,scaling=unconstrained,color=[red,black$2]);

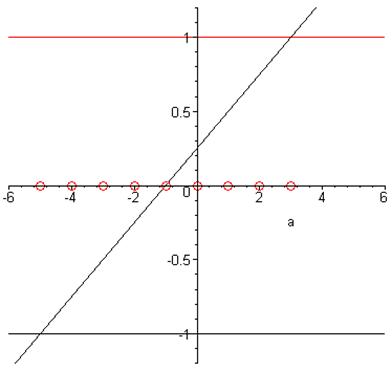
Графіка наочно показує результати розв’язання.

Приклад 27. Розв’яжіть систему рівнянь 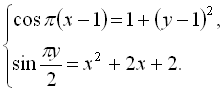У відповідь запишіть добуток , якщо – розв’язок системи рівнянь.

Розв’язання

Згідно з властивостями тригонометричних функцій, що та , отримаємо: 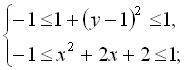звідки 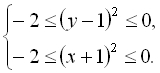Дана система нерівностей виконується лише при ; .

Тоді добуток .

Відповідь: .

В даному випадку ми маємо трансцендентні рівняння. Слід розуміти, що розв’язання трансцендентних, зокрема, тригонометричних, рівнянь є задачею складною для будь-якої системи символьної математики. Цей приклад зайвий раз показує, що вузький набір інструментів стандартного застосування системи далеко не завжди приводить до успіху. Дійсно, спробуємо знайти розв’язок системи рівнянь:

> restart:

with(RealDomain):

Warning, these protected names have been redefined and unprotected: Im, Re, ^, arccos, arccosh, arccot, arccoth, arccsc, arccsch, arcsec, arcsech, arcsin, arcsinh, arctan, arctanh, cos, cosh, cot, coth, csc, csch, eval, exp, expand, limit, ln, log, sec, sech, signum, simplify, sin, sinh, solve, sqrt, surd, tan, tanh

> solve({cos(Pi*(x-1))=1+(y-1)^2,sin(Pi*y/2)=x^2+2*x+2},{x,y});

Команда solve розв’язок знайти не змогла.

Спробуємо побудувати графіки заданих ліній. В даному випадку кожне з рівнянь подано у вигляді неявної функції. Для побудови графіків функцій, що задані неявно, в Maple існує команда plots[implicitplot]:

> plots[implicitplot](cos(Pi*(x-1))=1+(y-1)^2, x=-2..2,y=-2..2);

plots[implicitplot](sin(Pi*y/2)=x^2+2*x+2, x=-2..2, y=-2..2);

Графіки рівнянь відсутні!

Спробуємо застосувати команду наближеного знаходження розв’язків рівнянь та систем рівнянь

> fsolve({cos(Pi*(x-1))=1+(y-1)^2,sin(Pi*y/2)=x^2+2*x+2},{x,y},{x=-1.5..0,y=0.5..1.5});

І в такий спосіб успіху не досягли.

Перевіримо, чи задовольняє вихідну систему рівнянь розв’язок, знайдений ручним способом:

> subs(x=-1,y=1,[cos(Pi*(x-1))=1+(y-1)^2,sin(Pi*y/2)=x^2+2*x+2]);eval(%);

Ми впевнилися, що знайдений розв’язок систему задовольняє. Для того, щоб отримати наочну ілюстрацію, побудуємо графіки правих частин рівнянь

> plot([[y,1+(y-1)^2,y=-3..3],[x,x^2+2*x+2,x=-3..3],1], -3..3,0..4,linestyle=[1,3$2],thickness=[2,1$2], color=[red,green,black]);

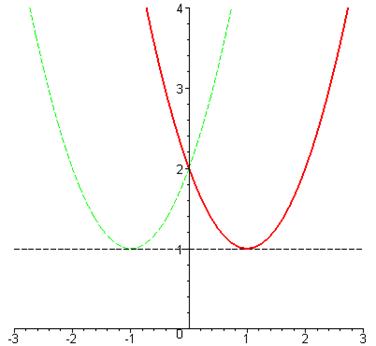
Із побудованих графіків видно, що тільки при , праві частини рівнянь досягають значення 1, залишаючись більше 1 при інших . Оскільки ліві частини рівнянь не можуть приймати значення більші за 1, то це означає, що за умови існування розв’язку наближений розв’язок дорівнює , . Команда fsolve знаходить розв’язок із будь-якою точністю. Але для цього потрібно вказати прийнятний відрізок, на якому знаходиться корінь.

> fsolve({cos(Pi*(x-1))=1+(y-1)^2,sin(Pi*y/2) =x^2+2*x+2},{x,y},{x=-1.1..-0.9,y=0.9..1.1});

Межі «прийнятного відрізка» потрібно визначати в кожному конкретному випадку методом підбору.

Приклад 28. Зазначте кількість розв’язків рівняння

на проміжку .

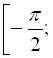
Розв’язання

ОДЗ: .

Кожний множник вихідного рівняння прирівняємо до нуля:

або

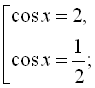
Отже загальний розв’язок можна записати у вигляді сукупності

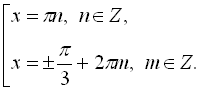А, враховуючи ОДЗ, коренями на проміжку

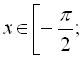
є і .

> restart:

with(RealDomain):

> solve(sqrt(sin(x))*(4-5*cos(x)-2*(sin(x))^2));

Перевіримо, чи задовольняють отримані розв’язки вихідне рівняння

> subs(x=0,sqrt(sin(x))*(4-5*cos(x)-2*(sin(x))^2));eval(%);

subs(x=Pi/3,sqrt(sin(x))*(4-5*cos(x)-2*(sin(x))^2));eval(%);

subs(x=-Pi/3,sqrt(sin(x))*(4-5*cos(x)-2*(sin(x))^2));eval(%);

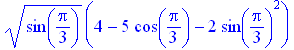
І в останньому випадку при 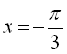система «не помітила», що корінь із від’ємного числа не існує. Якщо ж замість команди subs застосувати команду eval, сторонній корінь система розпізнає:

> eval(sqrt(sin(x))*(4-5*cos(x)-2*(sin(x))^2),x=0);

eval(sqrt(sin(x))*(4-5*cos(x)-2*(sin(x))^2),x=Pi/3);

eval(sqrt(sin(x))*(4-5*cos(x)-2*(sin(x))^2),x=-Pi/3);

Undefined – невизначений.

Відповідь: 2 розв’язки.

Приклад 29. Знайдіть усі дійсні значення параметра а, при яких рівняння має розв’язок.

Розв’язання

Замінимо через , тоді

, звідси .

Отже, рівняння набуває вигляду

. Розв’яжемо квадратне рівняння відносно змінної :

;

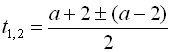
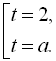
Зробимо оцінку , для цього розділимо обидві частини рівності на : 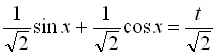; за допомогою введення допоміжного кута (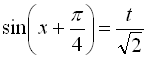І). Оскільки 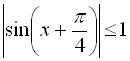, то й , тобто 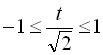, або .

Отже, не задовольняє наші умови, тому , а оскільки , то і , і з рівності (І)

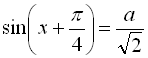
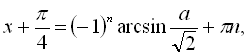
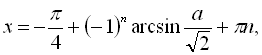
Відповідь: для розв’язків немає;

для .

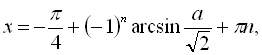
> restart:

В цьому прикладі Maple може допомогти на етапі дослідження функції

> minimize(sin(x)+cos(x), x=0..2*Pi, location=true);

maximize(sin(x)+cos(x), x=0..2*Pi, location=true);

Команди minimize та maximize допомогли визначити найбільше та найменше значення, що їх може приймати функція .

Отже, значення параметра а, при яких рівняння має розв’язок, визначаються умовою .

Оскільки , можемо записати

> trigsubs(sin(x)+sin(y));

subs(y=Pi/2-x,op(%));

eval(%);

_EnvAllSolutions:=true:

%%=a;

solve(%,x);

> about([_B1,_Z3]);

[_B1, _Z3]:

is used in the following assumed objects

[_Z3] assumed integer

[_B1] assumed OrProp(0,1)

За допомогою команди about ми дізналися, що одна із згенерованих системою змінних може приймати тількі цілі значення, а інша – тільки значення 0 або 1.

Система правильно знайшла корінь останього рівняння, але форма його виведення для нас незручна.

Приклад 30. Зазначте усі дійсні значення параметра а, при яких рівняння має розв’язки. Знайдіть ці розв’язки.

Розв’язання

Знайдемо ОДЗ:

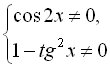
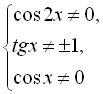
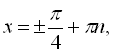
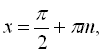
Оскільки перше й друге значення однакові, то в ОДЗ входять будь-які х, окрім (І) і (ІІ).

Перетворимо вихідне рівняння за допомогою тригонометричних формул: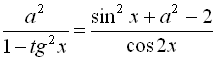

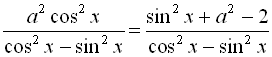Врахувавши ОДЗ:

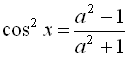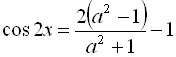
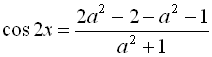
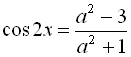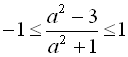
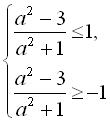
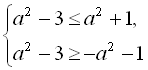
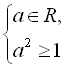
. Оскільки для будь-яких а, то ; згідно з формулою пониження степеня маємо . Оскільки , то й або 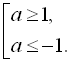Крім того, згідно з (І) і (ІІ), отримане рівняння 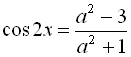має розв’язок, якщо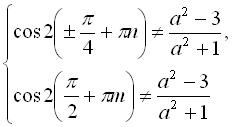

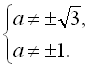
Отже, 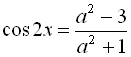для , , .

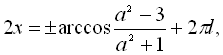
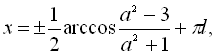
Відповідь: для і розв’язків немає.

для і .