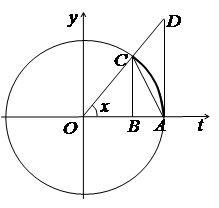2.2. Важливі границі
1) Перша важлива границя
Розглянемо функцію 
. Значення цієї
функції при 
не існує, але 
.
Теорема 2.1. Справедлива рівність
. (2.4)
Границю (2.4) називають першою важливою (першою чудовою) границею.
Доведення.
Нехай 
(x
вимірюється в радіанах).
|
Рис. 2.3 |
Розглянемо рис. 2.3, на якому позначено Виходячи з геометричних міркувань матимемо:
|
Оскільки , то, поділивши
останню нерівність на 
, матимемо:
або
.
Знайдемо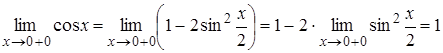 
,
.
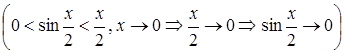Отже,
.
У випадку 
доведення проводиться
аналогічно. Тут маємо:
.
Об’єднаємо отримані результати:
.
Графік функції 
має
вигляд (рис. 2.4).
Рис. 2.4
2) Друга важлива границя
Теорема 2.2. Функція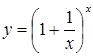 
при 
має границею число 
, тобто
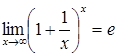. (2.5)
Границю (2.5) називають другою важливою (другою чудовою) границею.
(Зауважимо, що числом прийнято позначати границю такої збіжної
послідовності: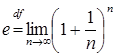 
, це число є ірраціональним (irrational) 
.)
Доведення.
Розглянемо випадок, коли . Нехай
.
Піднесемо члени отриманої нерівності до степенів,
показники яких є частинами нерівності 
.
Дістанемо
.
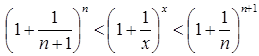Перейдемо до границі при 
.
Оскільки
,
,
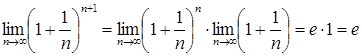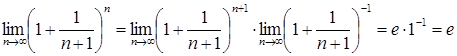то
.
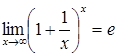Аналогічно доводиться справедливість рівності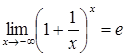 
.
Зауваження.
Якщо , то 
.
Поклавши 
,
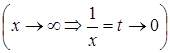матимемо іншу форму запису другої важливої границі
. (2.6)
Натуральний логарифм. Логарифм числа x за основою e називається натуральним логарифмом і
позначається 
.