1.5.1 Гравітаційне осадження частинок


В апаратах, які викори-сто­вують цей принцип вловлювання пилу, осадження завислих частинок від­бувається під дією сили ваги (гравітації). При падінні частинка пилу зазнає опору середовища. Найпростіше цей опір описується при прямолінійному і рівномірному русі кульової частинки, тобто в тому випадку, коли можна знехтувати турбулентністю потоку і конвенційними течіями.
Сила опору, що діє на частинку при її русі F, Н, може бути вира­жена рівнянням:
,                                       (1.17)
де       – коефіцієнт опору середовища;
          – площа перерізу частинки, перпендикулярного направленню  руху,   м2;
          – швидкість руху частинки, м/с;
          – густина газу, кг/м3.
        У  випадку  кульової  частинки   ,
де   dч – діаметр частинки, м.
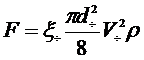,                                     (1.18)

 

Коефіцієнт  залежить від критерію Рейнольдса для частинки
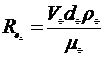,                                    (1.19)
де   – динамічна в’язкість газів, Па•с.

 

Ця залежність наведена на рис. 1.4.

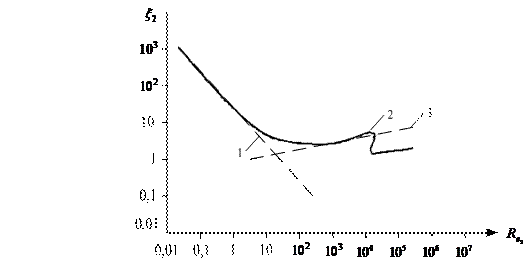
Рисунок 1.4 – Залежність коефіцієнта лобового опору кульової частинки  від критерію :
1 – область дії закону Стокса; 2 – стандартна крива; 3 – область дії формули Ньютона
Існує три різних режими руху кулеподібної частинки, кожному з яких відповідає певний характер залежності  від числа Рейнольдса. Так, для ділянок з ламінарним, турбулентним і перехідним режимами (Re ≤ 2;  Re > 500 і Re < 500) відповідно  = 24/Re;  = 0,44;  = 18,5/Re. На ділянці  з ламінарним режимом руху для частинок сферичної форми опір середо-вища описується законом Стокса:
         (1.20)

 

Для частинок розміром 0,2…2,0 мкм в рівняння (1.20) вводиться поправка Кенінгема-Мілікена, яка враховує підвищену рухомість части-нок, розмір яких порівнюється з середньою довжиною вільного пробігу газових молекул:
                              (1.21)

 

Поправка  розраховується за формулою

             (1.22)

 

В свою чергу,  можна розрахувати за формулою
                   (1.23)
де  Мг – маса 1 кмоль газів, кг/кмоль;
       – універсальна газова постійна, рівна  = 8314 Дж/моль•К;
       – абсолютна температура газів, К.
Для повітря при  = 20 і нормальному атмосферному тиску            = 6,5•10-8 м.

 

Відповідно до  рівняння (1.22) для повітря при нормальних умовах значення поправки  рівні:


,мкм

0,003

0,01

0,03

0,1

0,3

1,0

3,0

10,0

90,0

24,5

7,9

2,9

1,57

1,16

1,03

1,0

 

 

Розглянемо рух частинки в нерухомому середовищі під дією сили ваги (осадження). При відсутності опору середовища їх швидкість змінювалася б  залежно від часу  за законом . Проте, зі збільшенням швидкості буде рости величина опору середовища і відповідно зменшуватися прискорення частинки. Остаточно частинка буде рухатися з постійною швидкістю. Цю швидкість можна визначити з рівності сили опору середовища і сили ваги з врахуванням сили Архімеда:
,                       (1.24)
звідки                   ,                   (1.25)
де   – швидкість витання(осадження), м/с;
       – час релаксації частинки, с.

 

Величину швидкості витання  при гравітаційному осаджені частинок в повітрі можна визначити за допомогою графіка, наведеного на рис. 1.5.

 

 

    

 

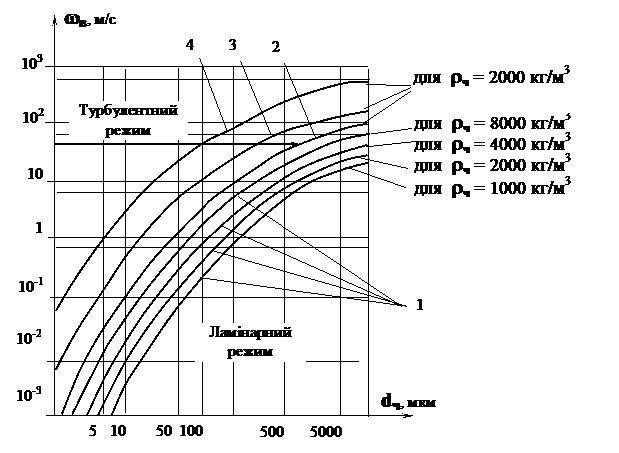
Рисунок 1.5 – Діаграма для визначення швидкості осадження частинок в повітрі:
1 – під дією сили ваги; 2…4 – під дією сили, яка перевищує силу
ваги відповідно в 10, 100, 1000 разів