1.5.3  Інерційне осадження частинок.


При обтіканні твердого тіла (чи краплини) запиленим потоком частинки внаслідок великої інерції продовжують рухатися поперек зігнутих ліній течії газів (рис. 1.6) і осаджуються на поверхні тіла. Таке осадження називається інерційним. Коефіцієнт ефективності інерційного осадження визначається долею частинок, витягнутих з потоку при обтіканні ними тіла. Деколи його називають „ефективністю мішені”.

 

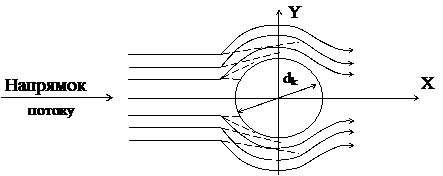
Рисунок 1.6 – Осадження частинок на кулі:
рух газів; ----------- рух частинок

 

Траєкторія руху частинки в газовому потоці може бути описана рівнянням:
,                          (1.31)
де    – об’єм частинки, м3;
        – час руху, с;
  – вектор швидкості, відповідно, частинки і газів в місці знаход-ження частинки, м/с.
Якщо газовий потік рухається стаціонарно, а частинка настільки мала, що для Fc можна застосувати закон Стокса (з поправкою Кенінгема-Мілікена), рівняння (1.31) можна записати у такому вигляді:
,                        (1.32)
де  – радіус-вектор частинки, м.
Рівняння (1.32) зручно привести до безрозмірного вигляду, ввівши такі значення:
 – безрозмірна координата частинки, де R – характерний розмір обтічного тіла (наприклад, радіус кулі чи циліндра в м);
 ­– безрозмірна швидкість газів, де  – швидкість газів, віддалених від обтічного тіла в м/с;
 – безрозмірний час.
Тоді, після відповідних підстановок і спрощень, одержимо:

,                                       (1.33)
де  – критерій Стокса, або „інерційний параметр”, який характеризує відношення інерційної сили, що діє на частинку, до сили гідравлічного опору середовища. Критерій чисельно рівний відношенню відстані, пройденої частинкою з початковою швидкістю Vr при відсутності зовнішніх сил до зупинки

до характерного розміру обтічного тіла (наприклад, діаметра кулі чи циліндра).

 

Якщо рух частинки здійснюється в ділянці, де закон Стокса не можна застосувати, необхідно ввести поправку, враховуючи відношення дійсної сили опору до стоксовського опору, рівну
,                              (1.34)
де  – критерій Рейнольдса для частинки.

 

Критерій   є єдиним критерієм подібності інерційного осадження. Це значить, що рівняння (1.33) застосовано до геометрично подібних сис­тем з однаковим значенням Re. У такому випадку подібність конфігурації лінії течії буде видержана незалежно від відмінності між швидкостями руху.
З рівняння (1.34) виходить, що при  (у частинок з безмежно малою масою)
,
тобто частинка точно проходить  лінією течії, не дотикаючись до поверхні обтічного тіла. Очевидно, таке явище буде спостерігатися і при достатньо малих значеннях критерію Стокса. Існує визначене мінімальне критичне значення числа Стокса , при якому інерція частинки є достатньою, щоб перебороти збільшення її газовим потоком, і вона досягає поверхні тіла. Таким чином, захоплення частинки тілом можливе при умові: .
За рис. 1.6 легко прослідкувати і вплив критерію Re на інерційне оса­дження. При ламінарній течії потоку ефективність оса­дження не буде залежати від цього критерію, поки можна нехтувати існу­ванням суміжного шару кругом обтічного тіла (в’язке обтікання). Зі збіль­шенням значення критерію Re при переході до турбулентного руху потоку на поверхні обтічного тіла утворюється суміжний шар, товщина якого зме­ншується зі збільшенням критерію Re. При значеннях Re більших критич­ного (Re > 500) лінії течії сильніше вигинаються (потенціальне обтікання) і обтікають тіло на  ближчій від нього відстані, внаслідок чого при тому ж значенні критерію  ефективність осадження буде вища. Це збільшення ефективності буде продовжуватися зі зменшенням товщини суміжного (ламінарного) шару кругом тіла, тобто зі збільшенням критерію Re.

 

Ще складніший характер набуває суміжний шар при розвинутій турбулентній течії потоку. Тому доцільно розглядати тільки системи з однаковим значенням критерію Re або системи, в яких режим руху потоку можна не враховувати при розрахунках.