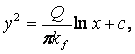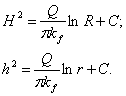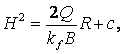5.6 Приплив води до водозабірних свердловин

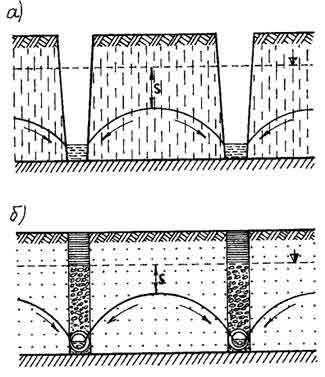
Для розробки системи водозниження, осушення будівельних котлованів та водопостачання використовують найбільш розповсюджений тип водозабірних споруд - свердловини. Якщо глибина свердловини (колодязя) досягає водоупору, тобто пронизує весь водоносний шар, то таку свердловину називають досконалою. У випадку, коли дно свердловини залишається у водоносному шарі, то її називають недосконалою (висячою). Свердловини, які розкривають безнапірні (ґрунтові) води, називають ґрунтовими.

При відкачуванні води з водоносного горизонту в самій свердловині і навколо неї на деякій відстані рівень води знижується, причому найбільше зниження має місце у свердловині, а чим дальше від неї, тим пониження рівня менше і на деякій відстані зовсім зникає. Це пояснюється опором руху води з боку частинок гірських порід.

Через деякий час після початку відкачування зниження рівня води у свердловині та навколо неї припиняється, а це означає, що кількість води, яка поступає до свердловини, дорівнює кількості води, яку з неї викачують, тобто встановлюється так званий динамічний рівень. Таким чином, навколо свердловини, з якої відкачують воду, утворюється депресійна поверхня. Крива, яка обмежує депресійну поверхню, називається депресійною кривою (рис. 5.13). Рух підземних вод до свердловини відбувається у вигляді радіального потоку.

Рисунок 5.13 - Приплив води до досконалої свердловини:

Н – потужність водоносного пласта; R – радіус кривої депресії;

r – радіус свердловини; S – зниження рівня води після відкачування;

h – висота зниженого стовпа води в свердловині

Для визначення дебіту (кількість води, яка може викачуватись протягом тривалого часу) досконалої свердловини використовують закон Дарсі. Відповідно до рис. 5.13 прийняті такі позначення величин:

Н - потужність водоносного шару, м;

h - динамічний рівень води у свердловині після зниження, м;

S - величина зниження рівня води, м;

R - радіус поверхні депресії, м;

r - радіус свердловини, м;

х та у- поточні координати, м.

Для того, щоб визначити дебіт, треба знати площу поверхні, через яку надходить вода до свердловини. Вода просочується через поверхню, концентричну з поверхнею самої свердловини, і являє собою поверхню циліндра з перемінними радіусом х та висотою у. Таким чином,

А=2х у.                                                  (5.11)

Гідравлічний градієнт на елементарній ділянці кривої депресії.

І = dy/dx.                                                  (5.12)

Підставляючи вирази (5.11) та (5.12) у формулу (5.2), одержимо

Q = 2k_f ху.                                        (5.13)

Розділимо перемінні х та у

2ydy=(Q/k_f)·(dx/x).                                (5.14)

Інтегруємо ліву та праву частини рівняння (5.14):

                                       (5.15)

де с - стала інтегрування.

Для визначення сталої інтегрування використаємо граничні умови. Згідно з розрахунковою схемою, перемінна у змінюється від h до H, а  х - від r до R  в межах потужності водоносного горизонту, причому якщо у = Н, то x = R, а при у = h х = r. Таким чином, маємо

                                        (5.16)

Віднявши від першого рівняння друге та розв'язавши відносно Q, одержимо:

                                        (5.17)

Ураховуючи, що H-h = S, формула (5.17) набуває такого вигляду:

                                       (5.18)

Цю формулу для визначення дебіту досконалої свердловини вперше одержав французький гідрогеолог Дюпюї. Щоб її використати, необхідно знати радіус депресії, величина якого залежить від типу гірської породи та її щільності. Він визначається за допомогою дослідних відкачувань, а для орієнтовних розрахунків можна приймати такі величини: крупкоуламкові та сильно тріщінуваті скельні породи - 400 - 600 м; пісок крупний - 200 - 400, пісок середньої крупності - 100 - 200; пісок дрібний 50 - 100; пісок пилуватий - 30 - 50; супісок – 20 - 40 м.

Крім того, радіус депресії можна визначити за емпіричною формулою І. П. Кусакіна

                                 (5.19)

де k_f вимірюється у м/с.

Ураховуючи, що одна доба складає 86400 секунд і H-h=S, одержимо

                                       (5.20)

У випадку недосконалої свердловини її дебіт визначається за формулою (5.18). У ній замінюють Н на Н_а.

                                   (5.21)

де Н_а - потужність активної зони від дзеркала ґрунтових вод, на яку розповсюджується відкачування води.

За Є. O. Замаріним потужність активної зони залежить від величини зниження рівня S та висоти стояння води у свердловині l і визначається такими співвідношеннями.

Величина зниження, м                   Потужність активної зони, м

S = 0,2 1                                                H_a = 1,3 1

S = 0,3 1                                                H_a = 1,5 1

S = 0,5 1                                                H_a = 1,7 1

S = 0,8 1                                                H_a = 1,85 1

S = 1                                                      H_a = 2,0 1

Для визначення припливу води до будівельного котловану, дно якого досягає водоупору, скористуємося законом Дарсі (формула (5.2)). У цьому випадку площа, через яку надходить вода до котловану, дорівнює

А = Ву,                         (5.22)

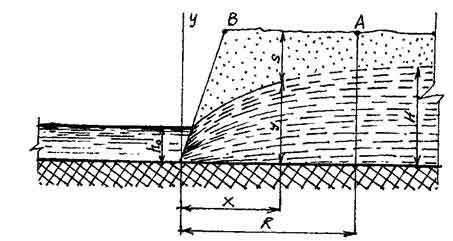
де В- ширина або довжина котловану, зі стінок якого просочується вода;

у - перемінні значення потужності водоносного горизонту в межах радіуса депресії (рис.5.14).

Рисунок 5.14 - Схема для визначення припливу води до будівельного котловану

Витрата води на будь-якій ділянці кривої депресії становить

                                    (5.23)

Розділивши перемінні та проінтегрувавши це рівняння, одержимо

                                (5.24)

де с - стала інтегрування.

Для визначення кількості води, що поступає в котлован, скористуємося граничними умовами: при x = R, у = Н, а при х = 0, у = h₀, таким чином:

                                (5.25)

                                            (5.26)

Віднявши друге рівняння від першого та вирішивши відносно Q, одержимо:

                              (5.27)

Якщо для водозниження влаштовують канаву, яка буде збирати воду з двох сторін при однакових умовах фільтрації, то величина припливу води до канави буде у два рази більшою

                                (5.28)