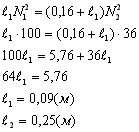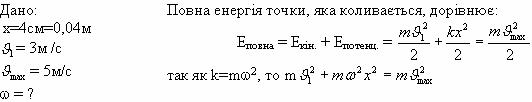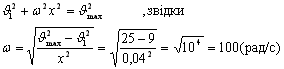

|
4.1.1. Приклади розв’язування задач
1. Рівняння коливань х = 0,1Sin (pt/8 + p/4 )см. Знайти: 1) максимальні значення швидкості та прискорення руху точки; 2) значення максимальної сили, що діє на точку; 3) повну енергію точки, яка коливається. Розв’язання:
Cos (
а = -0,001 ( Максимальне значення буде, якщо Sin amax = -0,001 Значення максимальної сили знайдемо: Fmax = mamax = -0,016 · 10-4 = -2, 46 · 10-6 (Н) Значення повної енергії знайдемо: Еповн = Відповідь: uмах = 3,9Ч10-4м/с; амах = -1,5Ч10-4м/с2; Fмах = -2,46Ч10-6Н; Еповн = 1,23Ч10-10 Дж. 2. Один маятник здійснив 10 коливань, другий за цей же час – 6 коливань. Різниця довжин маятників 16см. Знайти довжини маятників. Розв’язання
Розв’яжемо систему рівнянь:
Відповідь: 2. Якщо пружину з тягарцем розтягнути на 4см і надати швидкості 3м/с, то положення рівноваги він пройде зі швидкістю 5м/с. Знайти циклічну частоту коливань такого маятника. Розв’язання:
Відповідь: w =100 рад/с. 3. Визначити довжину хвилі при частоті 200 Гц, якщо швидкість розповсюдження хвиль 340м/с. Визначити швидкість звуку у воді, якщо джерело, що коливається з періодом 0,002с, збуджує у воді хвилі довжиною 2,9м. Розв’язання:
Відповідь: l1=1,7м; |
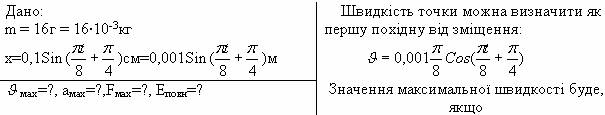
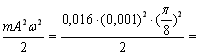 1,23·10-10 (Дж)
1,23·10-10 (Дж)