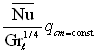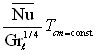Розділ 7. ТЕПЛООБМІН ПРИ ПРИРОДНІЙ КОНВЕКЦІЇ
7.1. Теплообмін при природній конвекції у великому об’ємі
Природна конвекція виникає в полі зовнішніх масових сил, які можуть мати різну природу. В окремому випадку полем зовнішніх масових сил може бути гравітаційне поле Землі. Цей випадок широко розповсюджений і носить назву теплової гравітаційної константи.
Гравітаційне поле Землі чинить вплив на рух рідини тільки при наявності в потоці вільних поверхонь чи неоднорідного розподілу густини. При відсутності вільних поверхонь і однорідному розподілі густини сила тяжіння, діюча на елемент об’єму, виділений у рідині, врівноважується архімедовою силою виштовхування і може не прийматися до уваги.
У загальному випадку при неоднорідному розподілі густини дія сили тяжіння не врівноважується архімедовою силою. На відміну від вимушених конвективних течій, поява яких обумовлена зовнішніми причинами, вільні чи природні течії виникають тільки під дією різниці густин, пов’язаній з неоднорідністю температурного поля в шарах рідин чи газів.
Дія зовнішніх масових сил у рівняннях руху в’язкої рідини враховуються членами ρgx, ρgу і ρgz, де ρ – густина рідини в загальному випадку така, що залежить від температури і тиску, а gx, gy і gz – проекції вектора прискорення поля масових сил на відповідні осі координат. При подальшому викладі під полем зовнішніх сил будемо розуміти гравітаційне поле Землі.
У цьому випадку сила тяжіння F на одиницю маси буде дорівнювати прискоренню вільного падіння g.
Для того щоб ввести в рівняння руху підйомну силу, перетворимо перші два члена, які стоять в правій частині цих рівнянь. І тоді для рівняння, записаного в проекції на ось х, отримаємо
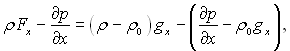 (7.1)
(7.1)
де Fx – проекція сили тяжіння на ось х; ρ0 – густина при деякій постійній температурі Т0 у будь-якій фіксованій точці потоку.
Вважаючи, що зміна ρ і Т малі в порівнянні з їх абсолютними значеннями, можна прийняти
![]() (7.2)
(7.2)
де 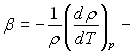 коефіцієнт об’ємного розширення рідини.
коефіцієнт об’ємного розширення рідини.
Член рівняння (7.1) ρ0gx можна представити в іншому виді ρ0gx = др0/дх, де через р0 позначимо гідростатичний тиск, розрахований за умови, що густина рідини у всіх точках об’єму постійна і рівна ρ0. Позначимо різницю р – р0 = р1, після елементарних перетворень рівняння (7.1) отримаємо
![]()
У цьому рівнянні ![]() представляє собою проекцію підйомної сили на одиницю об’єму рідкої частинки на ось х. При цьому вважаємо що густина рідини, яка оточує частинку з густиною
ρ,
скрізь постійна і рівна ρ0. Замість βρ зручніше
користуватися βρρ0 = βρ,, де
представляє собою проекцію підйомної сили на одиницю об’єму рідкої частинки на ось х. При цьому вважаємо що густина рідини, яка оточує частинку з густиною
ρ,
скрізь постійна і рівна ρ0. Замість βρ зручніше
користуватися βρρ0 = βρ,, де
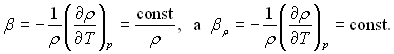
Тому що ρ мало змінюється з температурою, то коефіцієнт β часто приймають постійним і рівним середньому значенню в заданому інтервалі температур.
Аналогічним чином виводяться вирази для підйомної сили в рівняннях руху, записані в проекціях на осі у і z.
Природна конвективна течія часто зустрічається в природі і техніці і виникає, наприклад, біля вертикально поставленої нагрітої пластини чи горизонтально розташованого нагрітого циліндра чи тіла іншої конфігурації.
Якщо така течія виникає в великому об’ємі, то вона має властивості характерні для пограничного шару. Різка зміна швидкості і температури спостерігається тільки у відносно тонкому пристінному шарі. Властивості, характерні для пограничного шару, проявляються особливо чітко, коли теплопровідність і в’язкість рідини малі. Прикладами середовищ з малими значеннями теплопровідності і в’язкості можуть служити вода і повітря.
Якщо при вимушеному русі середовища з постійними фізичними властивостями поле швидкостей в рідині не залежить від температурного поля, то в умовах природної конвекції швидкісне поле безпосередньо зв’язане з розподілом температури і густини в полі течії. Це викликано тим, що підйомна сила є причиною вільного руху, який залежить від різниці температур у даній точці і деякої фіксованої точки потоку.
Течію в пограничному шарі при природній конвекції на нагрітій пластині можна бачити за допомогою різних оптичних методів. З цією метою паралельно нагрітій поверхні спрямовується пучок світла, який проходячи нагрітий пограничний шар, робить на екрані позаду тіла тіньове зображення, яке дозволяє судити про товщину пограничного шару і про місцевий коефіцієнт тепловіддачі.
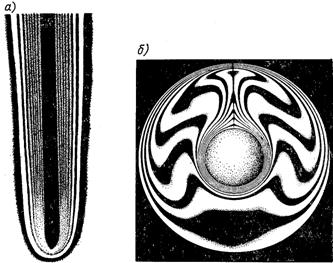
Рис.7.1. Температурний пограничний шар на вертикальній нагрітій пластині (а) і в кільцевому просторі (б)
Тіньове зображення виникає завдяки існуванню градієнта густини в середовищі навколо тіла. Відхилення променів пропорційне градієнту густини біля поверхні тіла і, як наслідок, тепловому потоку.
Крім тіньового методу дослідження широко розповсюджений метод, який ґрунтується на інтерференції світла. На рис.7.1,а,б наведені знімки температурного пограничного шару на вертикальній нагрітій пластині і в кільцевому просторі в умовах природної конвекції, отримані методом інтерферометричних смуг. Розшифровка такої інтерферограми дозволяє отримати не тільки якісні, але і досить точні кількісні результати. Так, інтерферометричні дослідження дозволяють отримати дані про картину ізотерм, температурних полях і локальних коефіцієнтах тепловіддачі.
У залежності від розмірів пластини, різниці температур пластини і оточуючого середовища, фізичних властивостей рідини чи газу, які оточують пластину, течія в пограничному шарі при обтіканні пластини (в умовах вільної конвекції) може мати ламінарну чи турбулентну форму.
Інтерферометричні виміри показали, що при природній конвекції на вертикальній пластині перехід ламінарного режиму течії до турбулентного настає при Rax > 7·1010, де Raх – число Релея, рівне добутку числа Грасгофа Grх на число Прандтля Pr.
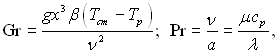
де х – повздовжня координата, яка відраховується від нижньої кромки вертикальної пластини у випадку Тст > Тр і від верхньої кромки пластини у випадку Тр > Тст; g – прискорення вільного падіння; Тст і Тр – температура поверхні пластини і температура не подразненого потоку відповідно; μ, λ і ср – динамічна в’язкість, теплопровідність і питома теплоємність при постійному тиску; β = – (1/ρ)(др/дТ)р – коефіцієнт об’ємного розширення середовища, що оточує пластину (для ідеального газу β = 1/Тр); ρ – густина; ν = μ/ρ і а = λ/(срρ) – кінематична в’язкість і температуропровідність середовища відповідно.
Таким чином, в залежності від величини х на різних ділянках одної і тої ж пластини можливі як ламінарний, так і турбулентний режими течії у пограничному шарі.
Тепловіддача вертикальної пластини при природній конвекції вивчалася експериментально і теоретично багатьма вченими. Для математичного опису розглядуваного явища можна використати рівняння руху і енергії зі спрощеннями, характерними для течії в пограничному шарі. Ці рівняння відомі під назвою рівнянь пограничного шару для стаціонарних вільноконвективних течій, мають наступний вид:
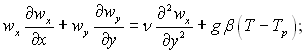 (7.3)
(7.3)
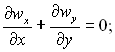 (7.4)
(7.4)
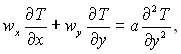 (7.5)
(7.5)
де wx і wy – складові вектора швидкості вздовж осей х і у; ось х спрямована вздовж пластини, ось у – по нормалі до пластини.
На відміну від випадку чисто вимушеної течії в рівняннях (7.3)...(7.5) є член, який враховує підйомну силу gβ(T – Tp), що представляє собою різницю між архімедовою силою виштовхування і силою тяжіння.
Раніше, при виводі рівнянь пограничного шару (див. § 6.1.1), було показано, що тиск р вздовж нормальної до пластини координати у практично не змінюється і його можна прийняти рівним тиску поза пограничним шаром. Тому що на відстані від пластини тиск дорівнює гідростатичному тиску р0 в даному перерізі х, то р(х) = р0(х). Отже, для вертикальної пластини р1=р–р0=0 і др1/дх = 0. З цієї причини член др1/дх, який з’явився в рівнянні руху після введення підйомної сили, в рівнянні (7.3) випущений.
Аналітичний розв’язок системи рівнянь пограничного шару для ламінарного режиму руху був проведений Е.Польгаузеном, який показав, що після введення функції току, можна отримати наступні співвідношення для цього випадку
![]() (7.6)
(7.6)
І тоді рівняння в частинних похідних (7.3)...(7.5) можна привести до системи двох звичайних диференціальних рівнянь. Для цього застосуємо наступне перетворення подібності: замість незалежних змінних х і у введемо нову змінну η =Су/х1/4, а замість невідомої функції току ψ – нову невідому функцію
![]()
де
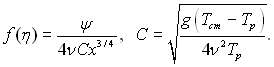 (7.7)
(7.7)
Тоді в нових змінних складові вектора швидкості wx і wy становитимуть:
![]()
Підставляючи ці вирази у рівняння (7.3)...(7.5) і вводячи безрозмірне відношення температур Θ = (Т – Тр)/(Тст – Тр), отримаємо два звичайні диференціальні рівняння для визначення невідомих функцій f(η) і Θ(η):
![]() (7.8)
(7.8)
![]() (7.9)
(7.9)
Система рівнянь (7.8) і (7.9) розв’язана для граничних умов І роду:
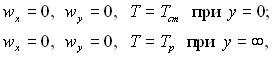
які в нових змінних приймають наступний вид:
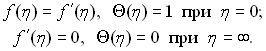
Послідуючий перехід до старих невідомих функцій wx, wy, T і незалежних змінних х і у дозволяє розрахувати швидкісне і температурне поля в рідкому чи газоподібному середовищі, яке оточує пластину.
Розв’язок цих рівнянь для різних значень чисел Прандтля графічно наведений на рис.7.2 і 7.3.
Ці рівняння можна використовувати як для випадку охолодження пластини (Tcm > Tp), так і для випадку нагрівання (Tcm < Tp).
З розв’язку виходить, що товщина динамічного і температурного пограничних шарів пропорційна х1/4.
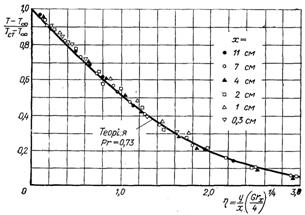
Виконані дослідження наведені на рис.7.4 і 7.5 підтверджують надійність теоретичних розрахунків наведених на рис.7.2 і 7.3
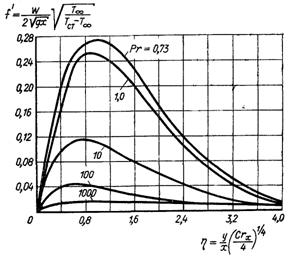
Рис.7.2. Залежність f ′ від η при різних значеннях чисел Прандтля
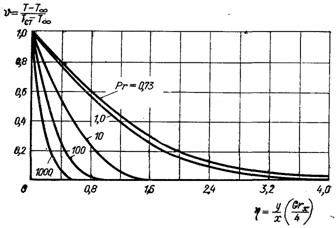
Рис.7.3. Залежність Θ від η при різних значеннях чисел Прандтля ↓
Рис.7.4. Порівняння результатів розрахунку з дослідними даними
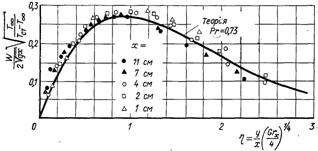
Рис.7.5. Порівняння результатів розрахунку з дослідними даними
За розподілом температур у пограничному шарі на пластині легко розрахувати кількість теплоти, яка переходить від пластини до рідини, оскільки з законом теплопровідності Фур’є
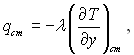 (7.10)
(7.10)
де qcm – локальне (місцеве) значення густини теплового потоку на поверхні пластини, яке залежить від х; λ – коефіцієнт теплопровідності середовища.
З іншого боку, у відповідності до закону охолодження Ньютона, згідно з яким густина теплового потоку пропорційна різниці температур поверхні твердого тіла і оточуючого середовища,
![]() (7.11)
(7.11)
де αх – локальне значення коефіцієнта тепловіддачі.
Переходячи від Т до безрозмірного параметра Θ, з виразу (7.10) отримаємо
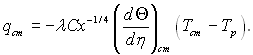 (7.12)
(7.12)
Результати розв’язку рівнянь (7.3)...(7.5) показали, що для повітря (dΘ/dη) = – 0,508. Із формул (7.11) і (7.12) можна отримати вираз для визначення локального числа Нуссельта на пластині:
![]() (7.13)
(7.13)
де Nux = αxx/λ; Grx = gx3β(Tcm – Tp)/ν2, αx – локальне значення коефіцієнта тепловіддачі.
З формули (7.13) виходить, що αx ~ 1/х1/4 і зменшується в напрямку руху середовища.
При необхідності можна розрахувати повну кількість теплоти, яка переходить від пластини до оточуючого середовища:
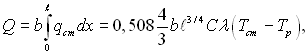
де b – ширина; ℓ – довжина пластини (враховується тепловіддача з одного боку пластини).
Якщо ввести поняття середнього коефіцієнта тепловіддачі, отримаємо
![]()
де
α| – середнє на поверхні пластини значення коефіцієнта тепловіддачі; ![]() – середнє значення числа Нуссельта, рівне
α| ℓ/λ.
– середнє значення числа Нуссельта, рівне
α| ℓ/λ.
Введемо число Грасгофа (Grℓ) і замінимо С його значенням з рівняння (7.7), отримаємо рівняння подібності для розрахунку тепловіддачі від пластини до повітря:
![]() (7.14)
(7.14)
в якому Grℓ = gℓ 3β(Tcm – Tp)/ν2, (Tcm = const).
Про вплив числа Прандтля на інтенсивність тепловіддачі при ламінарній природній конвекції можна судити за такими даними (де Raℓ = GrℓPr – число Релея, побудоване з використанням визначального розміру ℓ):

Також теоретично досліджені граничні випадки, які відповідають Pr→0 і Pr→∞. Оказалося, що при Pr→0 ![]() а при Pr→∞
а при Pr→∞ ![]()
Розглядувану вище задачу можна також розв’язати наближеним методом інтегральних співвідношень. Цей метод дає наступну залежність:
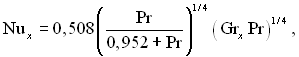 (7.15)
(7.15)
яка при 10–2< Pr < 103 з похибкою, яка не перевищує 10%, погоджується з точним рішенням.
Задача природної конвекції на вертикальній пластині може бути розв’язана і в тому випадку, коли на поверхні пластини заданий постійний тепловий потік
![]()
а температура поверхні невідома (гранична умова ІІ роду).
За цієї умови система диференціальних рівнянь в частинних похідних (7.3)...(7.5) може бути приведена до двох звичайних диференціальних рівнянь за допомогою наступної заміни змінних:
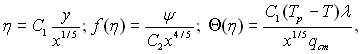 (7.16)
(7.16)
де
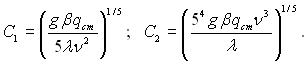 (7.17)
(7.17)
У нових змінних з урахуванням залежностей (7.6) і (7.16) складові вектора швидкості набудуть виду
![]() (7.18)
(7.18)
Підставляючи отримані вирази в систему рівнянь (7.3)...(7.6), отримаємо два звичайні диференціальні рівняння:
![]() (7.19)
(7.19)
![]() (7.20)
(7.20)
які можна розв’язати числовими методами із залученням ЕОМ.
У нових змінних граничні умови в системі рівнянь (7.19), (7.20) записуються наступним чином:
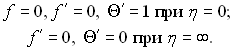
Результати розв’язку системи рівнянь (7.19), (7.20) зручно узагальнити у вигляді наступних формул:
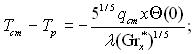 (7.21)
(7.21)
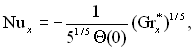 (7.22)
(7.22)
де ![]() модифіковане локальне число Грасгофа;
модифіковане локальне число Грасгофа; ![]() число Нусельта; значення функції
Θ(0) в залежності від числа Pr становить:
число Нусельта; значення функції
Θ(0) в залежності від числа Pr становить:
Pr |
0,1 |
1,0 |
10 |
100 |
Θ(0) |
–2,7507 |
–1,3574 |
–0,76746 |
–0,46566 |
Ця задача, так само як і попередня, може бути розв’язана наближеним методом інтегральних співвідношень. Наближене вирішення дозволяє отримати формулу
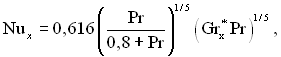
яку зручно порівнювати з формулою (7.15) для граничних умов І роду
Вважаючи у формулі (7.22) х = ℓ/2 і маючи на увазі, що при цьому qст=α(Тст–Тр)ℓ/2, отримаємо
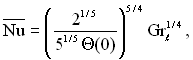 (7.23)
(7.23)
де
ℓ – довжина ділянки вертикальної пластини з ламінарним режимом течії в пограничному шарі; (Тст–Тр)ℓ/2 – різниця температур в перерізі х =
ℓ/2;
ℓ – коефіцієнт тепловіддачі, який ґрунтується на різниці температур (Тст–Тр)ℓ/2, ![]()
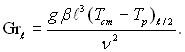
Величину ![]() , знайдену з формули (7.23) і отриману при рішенні задачі з граничними умовами ІІ роду (qст = const), доцільно порівнювати зі значенням
, знайдену з формули (7.23) і отриману при рішенні задачі з граничними умовами ІІ роду (qст = const), доцільно порівнювати зі значенням ![]() , яке відповідає точному розв’язку задачі природної конвекції на вертикальній пластині при граничних умовах І роду (Тст = const). Таке порівняння наведено в табл.7.1.
, яке відповідає точному розв’язку задачі природної конвекції на вертикальній пластині при граничних умовах І роду (Тст = const). Таке порівняння наведено в табл.7.1.
Таблиця 7.1.Вплив граничних умов на теплообмін при природній конвекції
|
Pr |
|
|
Pr |
|
|
0,1 1,0 |
0,224 0,543 |
0,219 0,535 |
10 100 |
1,11 2,07 |
1,10 2,07 |
З даних, наведених в табл.7.1, виходить, що безрозмірний комплекс ![]() , побудований по різниці температур
ℓ/2 при qст = const, близький за значенням до
, побудований по різниці температур
ℓ/2 при qст = const, близький за значенням до ![]() , розрахованого для умов Тст = const.
, розрахованого для умов Тст = const.
Отримані рішення строго справедливі тільки для малих різниць температур (Тст–Тр), оскільки при розрахунках вважалося, що фізичні властивості газу чи рідини є сталими величинами. У дійсності вони змінні і залежать від температури. При розв’язку рівнянь (7.3)...(7.5) враховувалася тільки залежність ρ(Т) у члені, який виражає підйомну силу.
Зміна параметрів μ, λ, β, ρ, і ср з температурою при великих різницях температур пластини і середовища призводить до суттєвої зміни профілів температури і швидкості в пограничному шарі.
При змінних фізичних властивостях теплові потоки для випадку нагрівання і охолодження пластини за інших рівних умов не однакові.
Рівняння пограничного шару при змінних властивостях рідини чи газу приймають наступний вид:
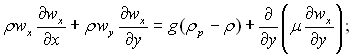 (7.24)
(7.24)
![]() (7.25)
(7.25)
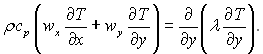 (7.26)
(7.26)
Ці рівняння, так само як і в випадку постійних фізичних властивостей, можна перетворити до системи двох диференціальних рівнянь, розв’язок яких значно простіша задача в порівнянні з системою рівнянь в частинних похідних.
Граничні умови для цієї системи не відрізняються від умов для розглянутого вище випадку постійних фізичних властивостей. Якщо вважати, що газ має властивості, які задовольняють співвідношення
![]() (7.27)
(7.27)
то система звичайних диференціальних рівнянь для змінних властивостей тотожно співпадає з раніше отриманою системою для постійних властивостей (7.8) і (7.9). Таким чином, усі вирішення, отримані для системи (7.8) і (7.9) стають сприйнятливими для газу, який володіє властивостями (7.27).
Аналіз впливу на теплообмін змінних фізичних властивостей газу з температурою, що ґрунтується на рішеннях зі спрощеннями запропонованими в (7.27), а також на безпосередньому числовому інтегруванні відповідної системи звичайних диференціальних рівнянь зі збереженням усіх членів, було викинено Спарроу і Грегом. У загальному випадку вважалося, що залежності λ(Т) і μ(Т) відповідають закону Сетерленда, тобто
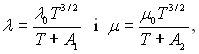 (7.28)
(7.28)
а зміна теплоємності з температурою лінійна. У формулах (7.28) А1 і А2 – деякі постійні, які залежать від роду газу; λ0 і μ0 – теплопровідність і динамічна в’язкість при 0 °С. Для повітря А1 = 201 К; А2 = 110,4 К; λ0 = 0,254·10–2 Вт/(м·К);
46·10–6
Па·с.
0 = 1,46·10–6 Па·с.
Шляхом співставлення результатів великої кількості рішень, отриманих при постійних і змінних властивостях середовища, було показано, що вплив залежності фізичних властивостей від температури для газів може досить точно враховуватися шляхом штучного введення певної визначальної температури
Т* = Тст – 0,3(Тст – Тр),
за якої параметри μ, λ, ср і Pr повинні підставлятися у формули (7.13) і (7.14), отримані для випадку постійних властивостей. При цьому вважається, що коефіцієнт об’ємного розширення β = 1/Тр, а число Прандтля змінюється в межах від 0,7 до 1.
Аналогічно цьому показано, що для ртуті за визначальну температуру необхідно приймати величину
Т* = Тст – 0,3(Тст – Тр),
до якої відносяться всі фізичні параметри, включаючи коефіцієнт β і число Pr.
Отримані результати підтверджені дослідним шляхом і показують їх справедливість у практично важливому діапазоні температур.
Для розрахунку тепловіддачі від широкої похилої пластини до повітря (Pr = 0,73) існує наступна формула:
![]() (7.29)
(7.29)
у якій 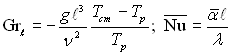 – середнє значення числа Нуссельта;
ℓ – довжина пластини;
φ – кут між нижньою частиною поверхні тепловіддачі пластини і вертикаллю. Формула (7.29) справедлива при 105 <
Grℓ <
109
і куті 0
<
φ <
90º.
При
φ =
0 пластина вертикальна, при
φ =
90° – горизонтальна (поверхня тепловіддачі обернена вниз).
– середнє значення числа Нуссельта;
ℓ – довжина пластини;
φ – кут між нижньою частиною поверхні тепловіддачі пластини і вертикаллю. Формула (7.29) справедлива при 105 <
Grℓ <
109
і куті 0
<
φ <
90º.
При
φ =
0 пластина вертикальна, при
φ =
90° – горизонтальна (поверхня тепловіддачі обернена вниз).
У випадку, коли поверхня тепловіддачі обернена вгору, застосовується формула
![]() (7.30)
(7.30)
яка справедлива для квадратних пластин при 105 < Ra < 2·107.
У цих формулах фізичні властивості середовища віднесені до температури 0,5(Тст – Тр). У формулі (7.30) за характерний розмір прийнята сторона квадрата. Цю формулу можна застосовувати у тих випадках, коли холодна сторона пластини спрямована вниз і Тст < Tp.
Як відмічалося на початку розділу, при Ra > 7·1010 течія в пограничному шарі переходить в турбулентну і формули, отримані для ламінарної області, стають неправомірними.
Для турбулентної природної конвекції поки не існує строгої теорії і інтенсивність переносу теплоти при турбулентному режимі може розраховуватися за формулами, отриманими емпіричним чи напівемпіричним шляхом.
Доказано, що при досить великих числах Релея інтенсивність теплопереносу, яка характеризується коефіцієнтом тепловіддачі α, в межах похибки вимірів не залежить від розмірів пластини, тобто показано, що число Нуссельта пропорційне Gr1/3.
Досліди, виконані з крапельними рідинами при числах Pr = 2,4...118, дозволили отримати наступну залежність для тепловіддачі вертикальної пластини при природній конвекції:
![]()
яка справедлива при 4·1010 < Raℓ < 9·1011.
Для квадратної горизонтальної пластини, поверненої нагрітою стороною вгору чи холодною – вниз, існує наступна формула, справедлива для турбулентної області
![]() (7.31)
(7.31)
У цій формулі характерним розміром є сторона квадрата, а фізичні властивості середовища віднесені до температури 0,5(Тст – Тр). Формула (7.31) справедлива при 2·107 < Ra < 3·1010.
Наведені залежності отримано шляхом опрацювання дослідних даних методами теорії подібності і справедливі в межах дослідних змін параметрів.