6.7.2. Пористе охолодження

Пористим охолодженням називається такий спосіб охолодження, коли охолоджувальний газ надходить в пограничний шар крізь проникливу, пористу поверхню. Якщо охолоджувальною субстанцією є рідина, то такий спосіб називають охолодженням “випотіванням”. У випадку пористого охолодження витрати охолоджувального газу в порівнянні з іншими способами газових завіс виходять мінімальними.

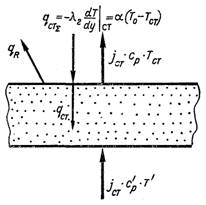
Рис.6.80. Схема теплових потоків при пористому охолодженні

На рис.6.80 наведена схема теплових потоків при пористому охолодженні. Тепловий потік від гарячого газу передається до поверхні пористого матеріалу і далі розповсюджується в глибину матеріалу за рахунок теплопровідності. Охолоджуючий газ, що проходить крізь пористий матеріал, акумулює цю теплоту і нагрівається до температури стінки. У цьому разі тепловий баланс для поверхні теплообміну можна записати так:

(6.571)

Розглянемо випадок наведений на рис.6.81, де заданими є параметри основного і охолоджувального газів і температура стінки і необхідно визначити витрати охолоджувального газу, необхідні для забезпечення заданої температури стінки.

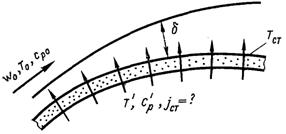
Рис.6.81. До розрахунку пористого охолодження

З рівняння (6.571) виходить, що

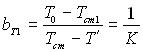(6.572)

чи (6.573)

Отже, рівняння енергії для плоского пограничного шару запишеться так:

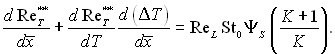(6.574)

З урахуванням рівнянь (6.574) і (6.241) маємо

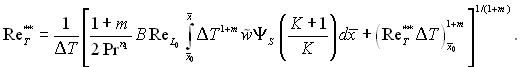(6.575)

Відносний закон теплообміну Ψ_S визначається за формулами (6.280) і (6.282).

Витрати охолоджувального газу крізь пористу стінку знаходимо з формули:

(6.576)

де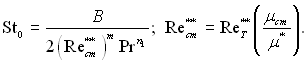

Для області дозвукових швидкостей течії газу при постійних значеннях Т_ст і Т′  і для граничних умов 0 при х( = 0 маємо

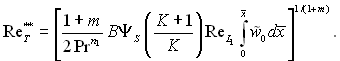(6.577)

У цьому випадку формула для витрат охолоджувального газу має вид

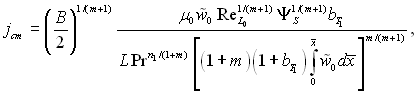(6.578)

а у випадку обтікання плоскої пластини (w̃₀  = 1)

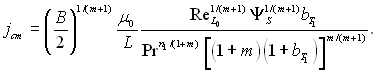(6.579)

Для ламінарного пограничного шару В/2=0,22 і т=1. Для турбулентного пограничного шару В/2=0,0128 і т=0,25.

Із формули (6.579) слідує, що для підтримування постійної температури пористої стінки витрати охолоджувального газу повинні зменшуватися по довжині пластини: для ламінарного пограничного шару j_cm ~ x^–0,5, а для турбулентного пограничного шару j_cm ~ x^–0,2.

Для степеневого закону зміни швидкості (w̃₀ = х^п) маємо

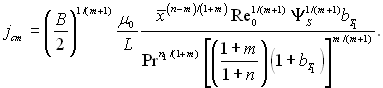(6.580)

На околиці будь-якої точки (п = 1) для ламінарного пограничного шару j_cm = const, а для турбулентного пограничного шару j_cm ~ x^–0,6.

Знаючи витрати охолоджувального газу j_cm, температуру поверхні теплообміну Т_ст і початкову температуру газу Т', можна визначити розподіл температур по товщині пористої поверхні.

6.8. Теплообмін при течії розріджених газів

Розвиток нових областей техніки і особливо космічної техніки викликає підвищений інтерес до дослідження процесів теплообміну в розріджених газах, коли необхідно брати до уваги дискретну структуру газу. Це приходиться робити у тих випадках, коли густина газу настільки мала, що середня довжина вільного пробігу молекул ℓ|  співрозмірна з характерним лінійним розміром L тіла чи процесу (товщиною пограничного шару, ударною хвилею, діаметром каналу та ін.).

З кінетичної теорії газів відомий наступний зв’язок між в’язкістю газу і довжиною вільного пробігу:

(6.581)

З іншого боку, середня швидкість молекул υ| зв’язана зі швидкістю звуку а співвідношенням

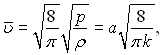(6.582)

де

За таких вихідних умов середня довжина вільного пробігу молекул буде

(6.583)

Середня довжина вільного пробігу молекул повітря залежить від висоти над рівнем моря.

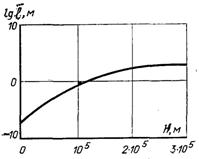
Рис.6.82.Зміна середньої довжини пробігу молекул повітря в залежності від висоти Н

Як видно з графіка (рис.6.82), при висоті 8·10⁴ м

середня довжина вільного пробігу молекул становить приблизно 25 мм, за таких умов повітря вже неможна розглядати як суцільну субстанцію, якщо лінійний розмір тіла має той же порядок.

З рівняння (6.583) виходить, що

(6.584)

Для Re << 1 маємо L/δ ≈ 1, і тому

(6.585)

Для великих значень числа Re з теорії ламінарного пограничного шару слідує, що L/δ ~ Re^0,5, тоді

Кn ~ M/Re^0,5 для Re >> 1, (6.586)

де Kn = ℓ/δ  – число Кнудсена.

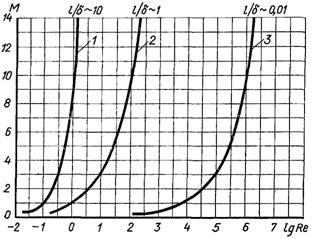
Рис.6.83. Області течії газу: 1 – вільно-молекулярнатечія; 2 – течія з ковзанням; 3– звичайна газова динаміка

Течія газу біля стінки, коли середня довжина вільного пробігу ℓ мала, але така, якою не можна нехтувати в порівнянні з розмірами тіла L чи товщиною пограничного шару δ, називається течією з ковзанням. Цьому типу течії відповідає інтервал 0,01 < ℓ/δ  < 1. На рис.6.83 в координатах М – Re ця область течії обмежена кривими ℓ/δ  = 1 і ℓ/δ  = 0,01.

Праворуч від кривої ℓ/δ  = 0,01 розташована область звичайної аеродинаміки, де справедливі допущення про континуум середовища.

Якщо довжина середнього вільного пробігу набагато більша за розміри тіла, то ця область називається вільно-молекулярною течією і на рис.6.83 визначається співвідношенням ℓ/L ~ M/Re > 10. У цій області зміни кількості руху молекул за рахунок ударів між собою на багато менші, ніж зміни за рахунок ударів молекул зі стінкою чи поверхнею тіла. Тому для розрахунку сил і теплових потоків тут достатньо розглядати удари потоку молекул зі швидкостями і енергіями, які розподілені у відповідності з тепловою рівновагою у вільному потоці, тобто за розподілом Максвела. В області між вільно-молекулярною течією і течією з ковзанням удари між молекулами газу і удари молекул газу зі стінкою однаково важливі.

Для кожної області течії повинні бути свої методи розрахунку теплообміну.

Повний обмін енергії між молекулами і стінкою характеризується коефіцієнтом термодинамічної акомодації

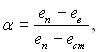(6.587)

де е_п, е_в – потоки енергії падаючих і відбитих молекул; е_ст – потік енергії, який виносився б від стінки при повному енергообміні, тобто за умови, коли енергія відбитих молекул відповідає температурі стінки.

Обмін імпульсом характеризується коефіцієнтом акомодації дотичного імпульсу

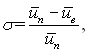(6.588)

де и_п і и_в – тангенціальні швидкості падаючих і відбитих молекул; и( – осереднене значення тангенціальної швидкості.

Якщо σ  = 0, відбиття молекул від стінки повністю дзеркальне, якщо σ = 1– дифузійне. Густина теплового потоку при вільно-молекулярній течії визначається за формулою

(6.589)

В одноатомному газі поверхнею сприймається тільки енергія поступального руху, тому

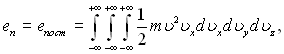(6.590)

де  υ – повна швидкість молекули в просторі; т – маса молекул; f – функція розподілу швидкостей.

Для рівноважного, максвелівського, розподілу швидкостей маємо

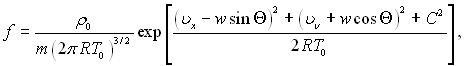(6.591)

де w швидкість не подразненого потоку.

Для багатоатомних газів необхідно враховувати внутрішню енергію молекул. Потік внутрішньої енергії молекул на поверхню становить

(6.592)

де j₁ = (5 – 3k)/(k – 1) – число ступенів свободи; N_n – число молекул, які падають на одиницю поверхні в одиницю часу:

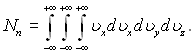(6.593)

Таким чином, для багатоатомних газів

(6.594)

Можна показати, що потік енергії відбитих від стінки молекул багатоатомного газу становить

(6.595)

Підставляючи е_п і е_ст в рівняння (6.589) і приймаючи акомодацію енергії однаковою за всіма ступенями свободи, далі інтегруючи вираз, отримаємо наступний вираз:

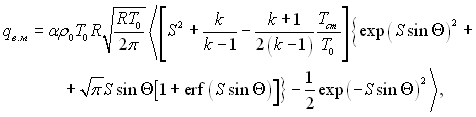(6.596)

де 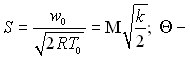кут атаки.

Для S >>1, тобто для області гіперзвукових швидкостей,

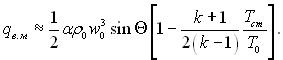(6.597)

Звідки при q_в.м = 0

(6.598)

Таким чином, у вільно-молекулярному потоці коефіцієнт поновлення не залежить від коефіцієнта акомодації. Температура теплоізольованої стінки у гіперзвуковому потоці газу перевищує температуру адіабатного гальмування. Значення величини дозволяє судити про напрямок теплового потоку. Якщо , то тепловий потік надходить до тіла. При тіло віддає набігаю чому потоку газу. Цей висновок справедливий для того випадку, коли розглядається тільки конвективний теплообмін. Але в реальних умовах руху тіл в розрідженій атмосфері необхідно враховувати випромінювання з поверхні тіла в навколишній простір.

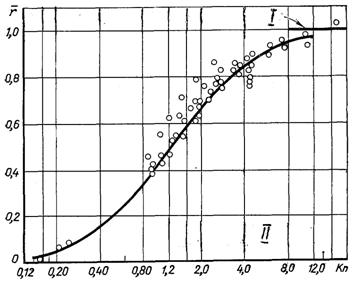
Рис.6.84. Залежність коефіцієнта поновлення від числа Кнудсена: І – теоретична межа вільно-молекулярного потоку; ІІ – дослідна межа ламінарного руху

На рис.6.84 наведена дослідна залежність коефіцієнта поновлення від числа Кнудсена при обтіканні пластини і циліндра повітрям. З рисунка видно, що вільно-молекулярний режим настає при Kn > 10.

Для інтенсивного охолод-ження тіла (S > T_cm/T₀) і повної акомодації (α  = 1) із формули (6.597) отримаємо

(6.599)

Це граничне значення теплового потоку складає половину енергії, що розсіюється, і приходиться на одиницю поверхні розрахованій за опором тіла в потоці з великими значеннями чисел Маха. Інтегруючи рівняння (5.596) по поверхні тіла, можна отримати вираз для сумарного теплового потоку тіла будь-якої форми.

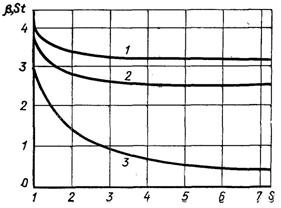
Рис.6.85.Теплообмін циліндра (1), сфери (2) і плоскої пластини (3) у вільно-молекулярному потоці

На рис.6.85 наведені результати таких розрахунків для нульового кута атаки при обтіканні циліндра, сфери і плоскої пластини. По осі ординат відкладений параметр

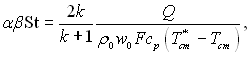(6.600)

де F – загальна поверхня тіла.

По осі абсцис відкладено параметр

Як видно з графіка, що при S > 3 закон теплообміну для циліндра, сфери і пластини, перпендикулярної до потоку, практично не залежить від числа М і тепловий потік визначається параметрами w₀ і ρ₀.

При коефіцієнті акомодації α рівному одиниці, граничні значення числа Стентона для повітря становлять: для пластини, нормальної до потоку, St=0,435, для сфери St=0,275 і для циліндра (вісь циліндра перпендикулярна до вектора швидкості) St=0,22.

Для пластини, паралельній потоку, граничне значення числа Стентона при дуже великих швидкостях прямує до нуля у відповідності з формулою

Для нерухомого газу (S = 0) з рівняння (6.596) для випуклих тіл отримуємо

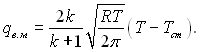(6.601)

Таким чином, з розрахункової точки зору вільно-молекулярний режим є відносно простим режимом, але певні труднощі виникають при визначенні коефіцієнта акомодації.

Коефіцієнт акомодації α, який входить до розрахункових формул, можна визначити тільки дослідним шляхом. Він залежить від природи газу і поверхні, на якій відбувається акомодація, а також від температури і тиску. На жаль, дослідні дані по коефіцієнтах акомодації недостатньо надійні і суперечливі. Досліди виявили залежність коефіцієнта акомодації від умов, при яких знаходиться поверхня до експерименту, що суттєво ускладнює узагальнення дослідних даних.

В області течії газу з ковзанням на поверхні тіла з’являються стрибки швидкості і температури. Для ілюстрації цього ефекту розглянемо течію газу між двома паралельно переміщуваними відносно одна іншої пластинами (так названа течія Куетта).

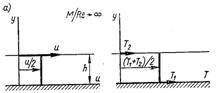
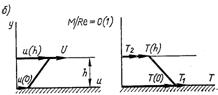
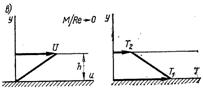
Рис.6.86. Течія газу з ковзанням між двома пластинами: а – вільно-молекулярна течія; б – течія в області континууму; в – течія з ковзанням

У вільно-молекулярному (рис.6.86) потоці (М/Re велике) молекули переходять від однієї стінки до іншої, не зустрічаючись між собою. Середня швидкість молекули становить и/2, а середня температура молекул дорівнює (Т₁+Т₂)/2, якщо обидві пластини мають однаковий коефіцієнт акомодації.

В області континууму (М/Re дуже мале) розподіл швидкостей і температур між двома пластинами лінійний і на поверхні пластин виконуються граничні умови звичайної аеродинаміки (умова “прилипання”). При проміжних значеннях М/Re, які знаходяться між 0,1 і 10, приймаються безперервні зміни швидкості і температури між пластинами, але ця безперервність порушується біля стінки і з’являються, як у вільно-молекулярному потоці, стрибок швидкості (ковзання) і стрибок температури.

Молекулярно-кінетична теорія газів з точністю до множника, близького до одиниці, дає значення ковзання і температурного стрибка біля стінки:

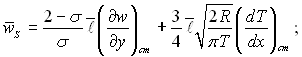(6.602)

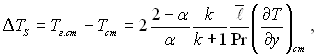(6.603)

де Т_г.ст. – температура газу біля стінки.

Величина називається коефіцієнтом стрибка.

Другий член у рівнянні для ковзання виражає вплив термомолекулярної течії – рух газу в напрямку збільшення температури.

Стрибки біля стінки, як і можна було чекати, пропорціональні середньому вільному шляху ℓ| і градієнтам швидкостей і температур на пластинах. Тому що при більших тисках ℓ| мале, то і ковзанням газу на стінці і температурним стрибком можна нехтувати, що і є обґрунтуванням гіпотези прилипання газу до стінки, яка приймається у звичайній газодинаміці.

При значенні Kn > 0,01 рівняння (6.602) і (6.603) можна ввести в граничні умови Нав’є-Стокса і енергії і розв’язувати задачу по визначенню коефіцієнтів тертя і теплообміну звичайними методами, які розглянуто у цьому розділі.

В окремому випадку, при обтіканні сфери можна зробити припущення, що в режимі з ковзанням теплообмін між газом і сферою радіусу R такий самий, як в безперервному потоці між газом і сферою радіусом R – ℓ| . З цього припущення виходить, що температурний стрибок створює додатковий термічний опір і зменшує коефіцієнт тепловіддачі. У цьому випадку розрахункова формула має вид

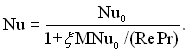(6.604)

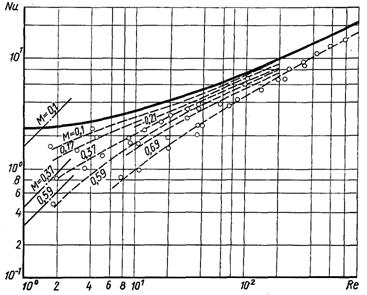
Рис.6.87. Теплообмін сфери в дозвуковому потоці розрідженого газу

На рис.6.87 наводиться співставлення дослідних даних з розрахунками за формулою (6.604) при коефіцієнті стрибка ξ = 3,42. Суцільна крива відповідає розрахунку для області континууму; штрихові – вільно-молекулярному режиму; лініями штрих-крапка подаються значення числа Nu в залежності від числа Re при різних значеннях чисел М. Як видно з рисунка, що зі збільшенням числа Рейнольдса вплив числа Маха зменшується.

Зменшення тепловіддачі за наявності стрибка температур широко використовується у техніці при створенні вакуумної ізоляції. В окремому випадку, в криогенній техніці широке розповсюдження отримала вакуумно-порошкова і вакуумна багатошарова ізоляція. Кращі зразки багатошарової ізоляції при тиску меншому 0,133 Па мають значення ефективної теплопровідності порядку 10⁴ Вт/(м·К).