6.6. Теплообмін при поперечному обтіканні труб
Під час проектування трубчастих теплообмінних апаратів, які знаходять широке застосування в техніці, необхідно знати закономірності конвективного теплообміну при поперечному обтіканні труби і пучка труб.
Розглянемо особливості поперечного обтікання одиночної циліндричної труби потоком нестисливої рідини. Як показують досліди, на довільній поверхні труби утворюється ламінарний пограничний шар, товщина якого поступово збільшується. При обтіканні лобової частини циліндра тиск у зовнішньому потоці зменшується (dp/dx < 0), швидкість у напрямку руху збільшується і частинки рідини в пограничному шарі, не дивлячись на гальмівну дію сил в’язкості, продовжують рухатися вздовж поверхні.
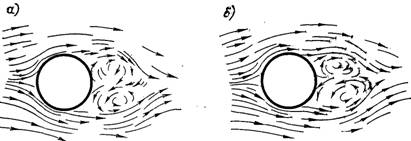
Рис.6.63. Обтікання циліндра з відривом ламінарного пограничного шару (а) і турбулентного пограничного шару (б)
У кормовій частині циліндра тиск у зовнішньому потоці починає зростати, частинки рідини у пограничному шарі під дією сил в’язкості і додатного градієнта тиску сповільнюють свій рух і починаючи з певного перерізу рухаються в зворотному напрямку, утворюючи вихори, які періодично відриваються від поверхні циліндра і виносяться потоком (рис.6.63). Точка відриву ламінарного пограничного шару знаходиться приблизно на куті φ = 82° і майже не залежить від числа Re. У цьому випадку тільки 45% поверхні циліндра обмивається безвідривно. Такий режим спостерігається при числах Re від 9 до (2...5)·105. При подальшому зростанні числа Рейнольдса ламінарний пограничний шар переходить в турбулентний і точка відриву турбулентного пограничного шару зміщується вниз за потоком до кута φ = 110...120° і біля 65% всієї поверхні циліндра омивається безвідривно.
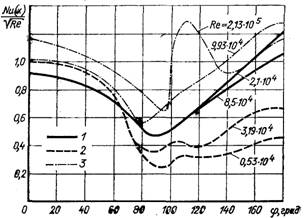
Рис.6.64. Зміна тепловіддачі за окружністю труби при різних числах Re:1, 2,3 – дослідні дані різних учених
Характер обтікання циліндричної труби визначає розподіл локальних коефіцієнтів тепловіддачі по поверхні циліндра (рис.6.64). Максимальне значення тепловіддачі спостерігається на лобовій частині твірної циліндра (φ = 0), де пограничний шар тонкий. На поверхні циліндра значення коефіцієнта тепловіддачі зменшується за рахунок збільшення пограничного шару і при φ = 90...100° досягає свого мінімуму . У кормовій частині труби відбувається руйнування пограничного шару і коефіцієнт тепловіддачі знову зростає. До точки відриву пограничного шару місцеву тепловіддачу на поверхні циліндра можна визначати за аналітичними формулами, викладеними в § 6.2 і 6.4. Аналітичний розрахунок середніх значень коефіцієнтів тепловіддачі практично не можливий з причини складної картини течії рідини в кормовій частині. Виходячи з цього, для розрахунків рекомендується використовувати рівняння подібності теплообміну.
Результати опрацювання дослідних даних в безрозмірних числах подібності наведені на рис.6.65. Дослідні дані добре узагальнюються формулами при Reрd = 5...1000:
(6.513)
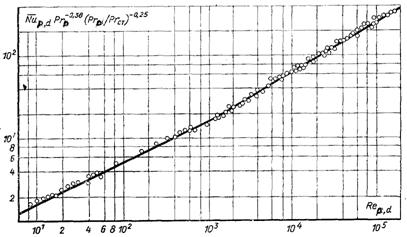
Рис.6.65. Середня тепловіддача при поперечному обтіканні циліндра. Порівняння дослідних даних з розрахунковими за формулами (6.513) і (6.514)
при Reрd = 1000…200000:
(6.514)
При розрахунках чисел подібності за визначальний розмір приймається зовнішній діаметр труби, а за визначальну температуру – середня температура рідини. Формули (6.513) і (5.514) справедливі для випадку, коли потік рідини спрямований по нормалі до твірної циліндра. Якщо кут між твірною циліндра і напрямком потоку ψ зменшується, то середня тепловіддача також зменшується. Цей ефект можна врахувати, якщо ввести у формули (6.513) і (5.514) поправочний коефіцієнт εψ = = αψ/α90°.
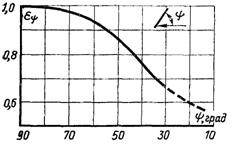
Рис.6.66. Вплив кута атаки на тепловіддачу циліндра
На рис.6.66 наведена залежність коефіцієнта εψ від кута ψ. В області зміни кута атаки від 30 до 90° можна використовувати наближену залежність
(6.515)
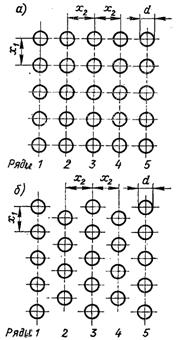
Рис.6.67. Розташування труб у пучках: коридорне (а) і шахове (б)
Трубчасті теплообмінники зазвичай виконують у вигляді пучків труб. Розміщення труб в пучках може бути різноманітне. Найбільше розповсюдження отримали шахові і коридорні пучки труб (рис.6.67).
Обтіканні трубки у пучці відрізняється від обтікання одиночної труби тим, що розміщенні поруч труби чинять вплив на цей процес. В окремому ряду при поперечному обтіканні, труби, які знаходяться поруч, утворюють звуження, що викликає зміну поля швидкості в порівнянні з обтіканням одиночної труби. Місце відриву пограничного шару зміщується вздовж за потоком. Труби, які розміщені в другому і подальших рядах, потрапляють в зону вихрового сліду від попередніх рядів, що безумовно впливає на коефіцієнт тепловіддачі.
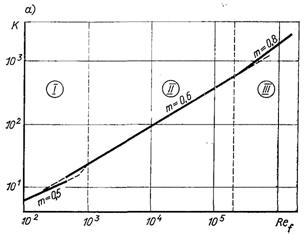
Рис.6.68. Тепловіддача при поперечному обтіканні за коридорного (а) і шахового (б) розташування пучків труб
Багато чисельні дослідні дані по середнім коефіцієнтам тепловіддачі в пучках труб, опрацьовані у вигляді чисел подібності наведені на рис.6.68. Отримані апроксимаційні залежності справедливі для глибинних рядів, тобто для тих ділянок, де потік гідродинамічно стабілізований. За визначальну температуру приймається температура набігаючого потоку, за характерний лінійний розмір – діаметр труби, а за розрахункову швидкість – швидкість в найменшому прохідному перерізі пучка.
Для пучків труб з числом рядів меншим 20 необхідно враховувати зменшення коефіцієнта тепловіддачі в перших рядах в порівнянні з глибинними рядами:
Значення коефіцієнта CZ визначається з рис.6.69.
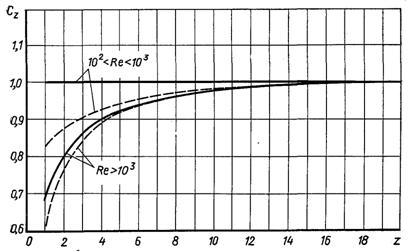
Рис.6.69. Поправка на число рядів при розрахунку тепловіддачі пучків: –––––––– – коридорний; -------- – шаховий
Під час проектування теплообмінних апаратів необхідно визначити оптимальну компоновку з точки зору капітальних затрат і експлуатаційних витрат. Досконалість теплової поверхні з енергетичної точки зору можна характеризувати співвідношенням переданої кількості теплоти через дану поверхню нагріву і енергії, яка тратиться на подолання опору:
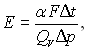(6.516)
де QV – об’ємні витрати, м3/с.
Для перепаду температур Δt = 1°С маємо
де параметр ε – кількість енергії, що йде на подолання опору, який приходиться на одиницю поверхні нагріву.
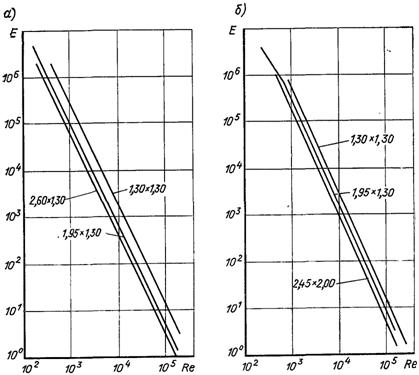
Рис.6.70. Ефективність тепловіддачі шахового (а) і коридорного (б) пучка труб в залежності від числа Рейнольдса і відстані між трубами
На рис.6.70 наведені результати розрахунку ефективності Е пучка труб діаметром 19 мм, який омивається потоком води при температурі 20 °С. З рисунка видно, що при числах Re від 500 до 50000 коридорне розташування труб ефективніше за шахове. Не дивлячись на те, що тепловіддача коридорних пучків у цій області менше, ніж шахових, ефективність коридорних пучків виходить більшою за рахунок менших гідравлічних втрат. При більш високих числах Re ефективність тепловіддачі зрівнюється і шахове розміщення труб в пучці стає трохи ефективнішим і вирішальним параметром у цій області є крок труб.
Ефективність тепловіддачі Е характеризує процес теплообміну тільки з енергетичної точки зору. При виборі конструкції теплообмінника необхідно враховувати і інші вимоги, і тільки сумісний розгляд експлуатаційних і капітальних затрат дозволяє вибрати оптимальний варіант теплообмінника.
6.7. Методи теплового захисту тіл від дії високоентальпійного газу
Основною тенденцією розвитку енергетичної техніки є збільшення максимальних температур і тисків теплоносіїв і робочих тіл. Максимальні температури газу в енергетичних установках набагато перевищують допустимі температури матеріалів, з яких робляться елементи проточної частини теплових машин і агрегатів. За цих умов суттєве значення для надійної роботи теплонапужених деталей має система охолодження.
Все більше застосування в техніці знаходять системи охолодження, які використовують плівкове і пористе охолодження.
6.7.1. Конвективний теплообмін при наявності газових завіс
У сучасній техніці для захисту поверхонь тіл від теплової дії високоентальпійного потоку газу широко використовуються газові завіси. Охолоджувальний газ подається на поверхню теплообміну і, розповсюджуючись вздовж цієї поверхні, створює теплову завісу. В деяких випадках газова завіса є як тепловим, так і хімічним захистом поверхні тіла.
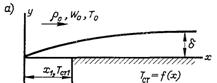
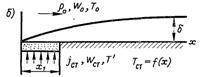
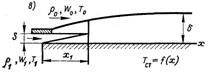
Рис.6.71. Схеми можливих конструктивних варіантів газових завіс
На рис.6.71,а-в наведені схеми основних конструктивних варіантів газових завіс. Можливі і різні комбінації з приведених варіантів. Наприклад, плівкове охолодження, яке широко використовується в рідинних реактивних двигунах, комбінується зі звичайним рекуперативним охолодженням стінки. Проточна частина реактивного твердопаливного двигуна зазвичай виконується у вигляді ділянок з різним теплоізоляційним покриттям і в цьому випадку газова завіса розповсюджується вздовж поверхні з поперечним потоком речовини.
Основним параметром, який визначає інтенсивність теплообміну при наявності газової завіси, є ефективність газової завіси
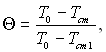(6.517)
де Т0, Тст і Тст1 – відповідно температури набігаючого потоку, теплоізольованої стінки і охолоджувального газу.
Таким чином, ефективність газової завіси визначається температурою теплоізольованої стінки за наявністю завіси:
(6.518)
Як буде показано, ця температура необхідна і для розрахунків теплообміну при наявності завіси. У більш загальному випадку при течії стисливого газу з хімічними реакціями ефективність газової завіси визначається через повні ентальпії:
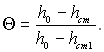(6.519)
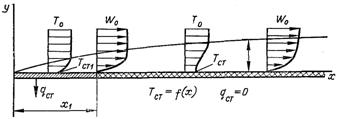
Рис.6.72. Теплова завіса
Для виводу формули ефективності газової завіси розглянемо повздовжнє обтікання плоскої поверхні потоком нестисливої рідини з постійними фізичними параметрами (рис.6.72). Ділянка довжиною х1 охолоджується, і температура стінки в перерізі х1 дорівнює Тст1, при цьому охолодження стінки на ділянці може здійснюватися будь-якими способами (відводом теплоти через стінку, вдуванням охолоджувального газу крізь пористу стінку чи щілину, плівкове охолодження та ін.). В області x > x1 стінка теплоізольована і температура стінки змінюється вздовж поверхні, наближаючись до температури набігаючого потоку. Радіаційним теплообміном нехтуємо.
Для області x > x1, qст = 0 рівняння енергії (6.60) запишеться так
(6.520)
після інтегрування цього рівняння в межах від х(1 до х(, отримаємо
(6.521)
Введемо параметр ефективності газової завіси, матимемо
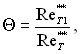(6.522)
де 
– число Рейнольдса в перерізі х(1.
Безумовно, рівняння (6.521) справедливе і для більш загального випадку, якщо замість температур ввести повні ентальпії.
Якщо б при x > x1 зберігалась би умова Тст = Тст1 = const, то число Рейнольдса по товщині втрати енергії 
визначалось би рівнянням
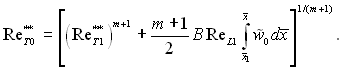(6.523)
Для пограничного шару на теплоізольованій поверхні при x > x1 повинні виконуватися наступні умови
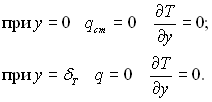(6.524)
Таким чином, всередині пограничного шару відбувається вирівнювання температури тільки внаслідок молекулярного чи турбулентного перемішування і підсмоктування газу із зовнішнього потоку. При цьому найбільша інтенсивність перемішування відбувається в пристінній області, де похідна дwx/ду максимальна. В наслідок цього профіль температури деформується так, щоб область дТ/ду ≈ 0 (чи Т = Тст = const) ,безперервно збільшувалася за х. Одночасно внаслідок підсмоктування газу із зовнішнього потоку температура в пограничному шарі наближається до температури Т0, тобто
при х→ 0 Т→Тст → Т0. (6.524)
Товщина втрат енергії, за визначенням
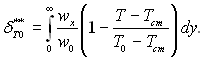
Отже, на теплоізольованій поверхні при х → ∞
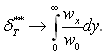(6.525)
Введемо коефіцієнт 
який відповідає граничним умовам
х→х1 β→1, а при х→∞ β→βmax, де
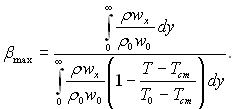(6.526)
Для ламінарного пограничного шару
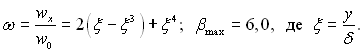
У більшості практичних випадків газова завіса застосовується в області великих чисел Рейнольдса і турбулентному пограничному шарі. Тоді, застосовуючи ω=ω0=ξ11/7, отримаємо βmax = 9,0.
З урахуванням рівнянь (6.522) і (6.523) за умови, що при х→ 0, β=βmax, отримаємо формулу для визначення ефективності газової завіси
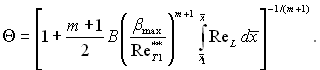(6.527)
Для ламінарного пограничного шару
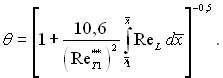(6.528)
Для турбулентного пограничного шару (т = 0,25, В/2 = 0,0128)
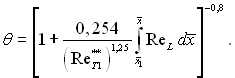(6.529)
В окремому випадку, при обтіканні плоскої пластини (ReL = const)
для ламінарного пограничного шару
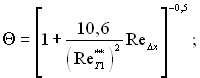(6.530)
для турбулентного пограничного шару
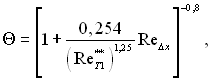(6.531)
де ReΔx = ρ0w0(x – x1)/μ0.
Якщо ввести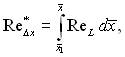 
то формули (6.530) і (6.531) можна розповсюдити на випадок довільного закону зміни швидкості вздовж поверхні тіла. В окремому випадку, у разі степеневого закону зміни швидкості 
, матимемо
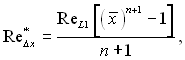(6.532)
де 
Тоді ефективність газової завіси ламінарного пограничного шару
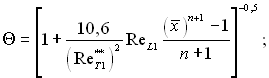(6.533)
а турбулентного пограничного шару
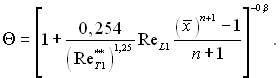(6.534)
З формул (6.533) і (6.534) слідує, що ефективність газової завіси зменшується для прискорених потоків (dw0/dx > 0, n > 0) і зростає для сповільнених потоків (dw0/dx < 0, n < 0).
Формулу (6.527) можна розповсюдити і на течію стисливого газу. З урахуванням рівнянь (6.302) отримаємо
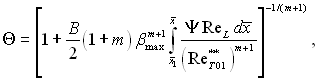(6.535)
де
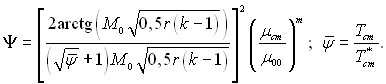(6.536), (6.537)
Отримані формули для ефективності теплової завіси, відтворюють схему організації, яка наведена на рис.6.73.
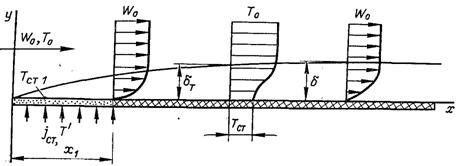
Рис.6.73. Газова завіса з пористою ділянкою
Інтегральне співвідношення енергії для проникливої поверхні при Тст = const
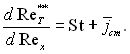(6.538)
Враховуючи, що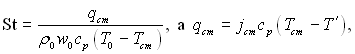 
отримаємо
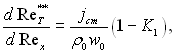(6.539)
де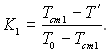 
Отже, при вдуванні охолоджувального газу крізь пористу пластину
(6.540)
де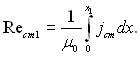 
При критичному вдуванні 
Формули для ефективності газових завіс при вдуванні газу крізь пористу стінку з урахуванням рівнянь (6.527) і (6.540) мають наступний вигляд:
для ламінарного пограничного шару
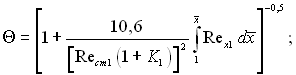(6.541)
для турбулентного пограничного шару
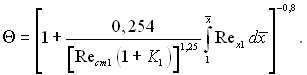(6.542)
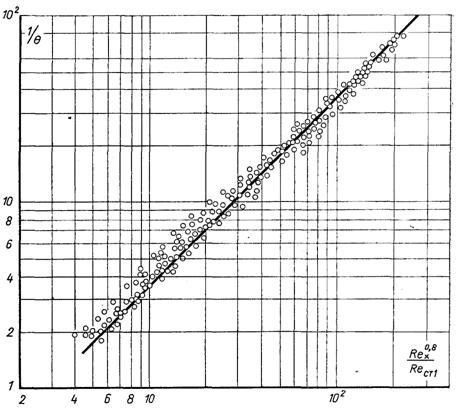
Рис.6.74.
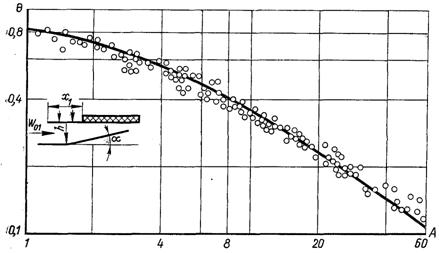
Рис.6.75 Ефективність газової завіси з пористою ділянкою при градієнтній течії: порівняння розрахункових за (6.542),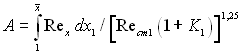 
і дослідних даних, помічених точками
На рис.6.74 і 6.75 порівнюються результати, отримані за формулою (6.542) з дослідними даними різних дослідників.
Для течії стисливого газу з урахуванням рівняння (6.535) отримуємо
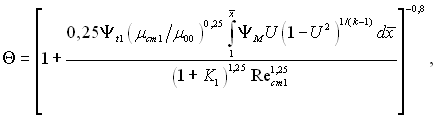(6.543)
де індекс “00” стосується параметрів гальмування.
Для течії газу в надзвуковому соплі з рівняння енергії для симетричного відносно осі пограничного шару отримаємо:
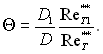(6.544)
З урахуванням рівняння нерозривності потоку для сопла
(6.545)
маємо
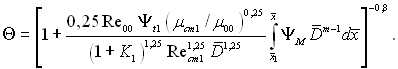(6.546)
Знаючи залежність діаметра сопла, а значить, і числа М від довжини х, визначаємо зміну ефективності газової завіси за довжиною сопла. Тому що в надзвуковій частині сопла ΨМ < 1, то з рівняння (6.546) виходить, що ефективність газової завіси у стисливому газі більша, ніж в нестисливій рідині.
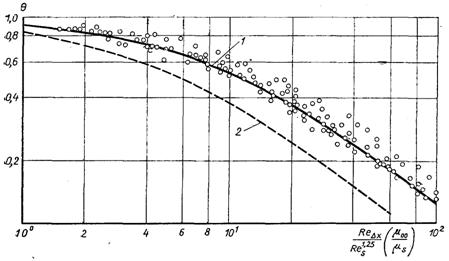
Рис.6.76. Ефективність газової завіси у надзвуковому потоці газу: 1 – розрахунок за формулою (6.543); 2 – розрахунок за формулою (6.542); точками позначені дослідні дані
На рис.6.76 наводиться співставлення дослідних даних по ефективності газової завіси у надзвуковому потоці з розрахунками по формулі (6.543) для випадку обтікання плоскої пластини (U = const).
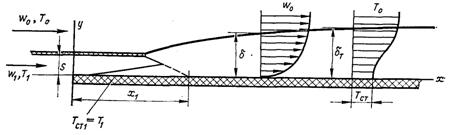
Рис.6.77. Схема щілинної газової завіси
Розглянемо газову завісу, яка створюється вдуван-ням охолоджувального газу крізь щілину (рис.5.77). Фізичні параметри основного і газу, що вдувається, приймаються однаковими і постійними.
На ділянці 0 < x < x1 пластина омивається тільки газом, що вдувається, і температура пластини дорівнює температурі газу вдування, тобто Тст=Тст1=Т1. У перерізі х = х1 починає розвиватися тепловий пограничний шар внаслідок перемішування завіси з основним потоком газу.
Використовуючи відомі залежності для турбулентних струменів, для області w1 < w0 можна вважати, що
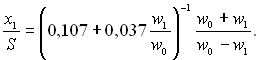(6.547)
У деяких випадках нехтуючи ділянкою х1, тобто вважаючи, що х = х1 ≈ х, чим отримуємо певний запас з ефективності газової завіси.
З рис.6.77 виходить, що для перерізу х1
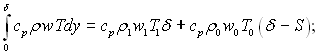(6.548)
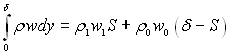. (6.549)
За визначенням, товщина втрат енергії
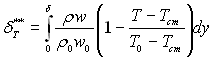(6.550)
і для перерізу х = х1, де Тст–Тст1, з урахуванням рівнянь (6.548) і (6.549),буде
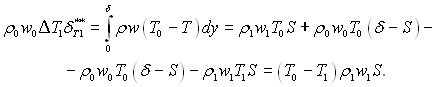(6.551)
Отже,
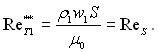(6.552)
Таким чином, ефективність газової завіси, створеної вдуванням охолоджувального газу крізь щілину визначається за формулами:
для ламінарного пограничного шару
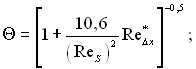(6.553)
для турбулентного пограничного шару
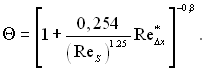(6.554)
На рис.6.78 наведені результати співставлення експериментальних даних різних дослідників з формулою (6.553).
Для випадку обтікання криволінійної поверхні потоком стисливого газу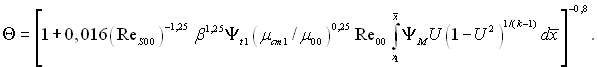 
(6.555)
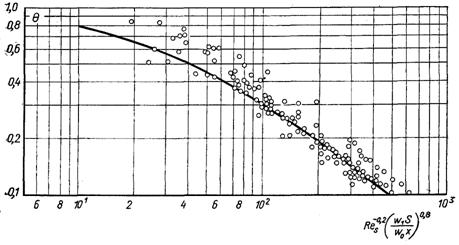
Рис.6.78. Ефективність газової завіси при щілинному вдуванні: співставлення розрахунків за (6.553) з дослідними даними різних авторів
Варто зауважити, що отримані формули для ефективності газової завіси можна розповсюдити і на вдування газу, який відрізняється від газу в набігаю чому потоці. У цьому разі ефективність газової завіси визначається через ентальпії газів:
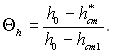(6.556)
При Sc = 1 повинна існувати подібність в розподілі ентальпії і повних концентрацій газу , що вдувається, тоді
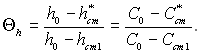(6.557)
Звідки
(6.558)
де 
– масова частка компоненти вдування на теплоізольованій стінці; Сст1 – масова частка компоненти вдування на стінці в перерізі х1.
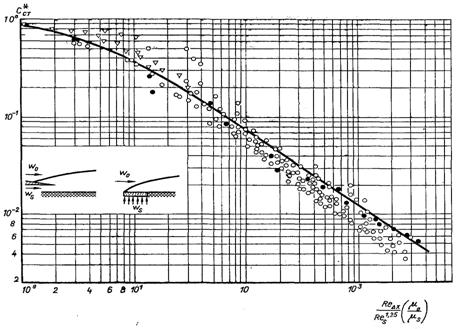
Рис.6.79. Ефективність газової завіси при вдуванні стороннього газу: лінія – розрахунок за (6.562); точки – дослідні дані
На рис.6.79 співставленні між собою розрахункові дані масових часток газу вдування на теплоізольовану стінку з дослідними даними.
Для визначення температури теплоізольованої стінки при вдуванні стороннього газу запишемо рівняння для теплоємності бінарної суміші газів на стінці
(6.559)
З рівняння (6.556) виходить, що
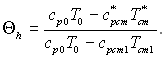(6.560)
Звідки з урахуванням (6.559) маємо
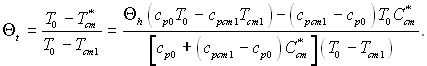(6.561)
У випадку вдування стороннього газу крізь тангенціальну щілину С0 = 0; Сст1 = 1; срст1 = срS і з рівняння (6.561) отримуємо
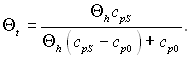(6.562)
Температура теплоізольованої стінки становить
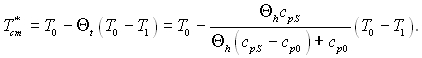
Таким чином, з ростом теплоємності охолоджувального газу при інших рівних умовах температура теплоізольованої стінки зменшується
Як правило, газова завіса застосовується разом зі звичайним охолодженням, і необхідно вміти визначати локальні коефіцієнти тепловіддачі і теплові потоки для цих умов.
Інтегральне співвідношення енергії для області x > x1 можна записати так:
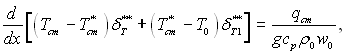(6.563)
де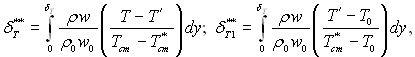 
(6.564), (6.565)
Т*ст. – температура ізольованої поверхні; Т′ – температура в даній точці в пограничному шарі на ізольованій поверхні.
У відповідності з рівнянням (6.520)
(6.566)
Тоді
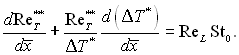(6.567)
де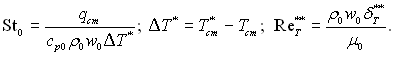 
Таким чином, інтегральне співвідношення енергії для поверхні теплообміну за наявності газової завіси зберігає звичайний вид, якщо замість ΔТ підставити ΔТ* = Тст – Т*ст. і товщину втрат енергії визначати за формулою (6.565).
Вважаючи, що закон теплообміну у вигляді рівняння (6.241) справедливий і для розглядуваних умов, якщо 
визначити з рівняння (6.565), а St – по рівнянню (6.567), тобто
(6.568)
Інтеграл рівняння енергії з урахуванням (6.568) має вид
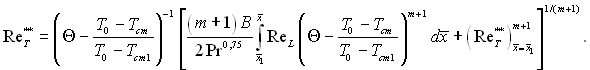(6.569)
З урахуванням рівняння для
Θ з рівняння (6.569) визначаємо 
і за рівнянням (6.568) – локальні значення числа Стентона. Величина локальних теплових потоків в стінку визначається за формулою
(6.570)
де 
а ефективність завіси
Θ знаходиться з формули (6.554).
