6.5.2. Теплообмін при турбулентній течії рідини в трубах

При Re > 2000 ламінарна течія рідини в трубі стає нестійкою і переходить в турбулентну. При цьому інтенсивність переносу імпульсу, теплоти за радіусом труби суттєво збільшується. Виходячи з цього при розрахунках процесів тепло і масообміну при течії рідини в трубах в першу чергу необхідно визначити режим течії.

Розглядаючи сили, діючі на елементарний циліндр радіусу R при стабілізованій течії рідини в області розвиненої течії, з умов їх рівності отримуємо

(6.420)

Звідки дотична напруга на стінці труби становить

(6.421)

де ξ – безрозмірний коефіцієнт опору, який визначається з формули

(6.422)

Вперше дослідні дані з коефіцієнтів опору під час течії рідини в гладких трубах були отримані Блазіусом і узагальнені емпіричною формулою

(6.423)

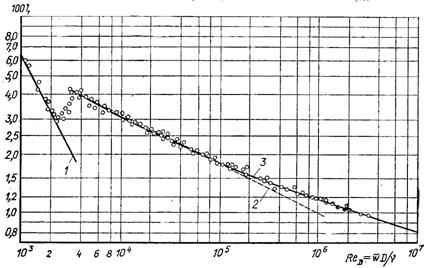
Рис.6.53. Закон опору для течії рідини в гладкій трубі: 1 – ламінарний рух (6.333);

2 – турбулентний рух (6.423); 3 – турбулентний рух (6.433)

Як видно з рис.6.53, ця формула справедлива до значень Re_D < 10⁵. При більших значеннях чисел Re_D спостерігається певне відхилення дослідних даних від формули Блазіуса.

Дослідження показують, що розподіл швидкостей за діаметром труби при турбулентній течії рідини з достатньою точністю описуються степеневою залежністю

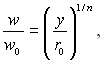(6.424)

де у – відстань від стінки труби; y = r₀ – r. Показник степеня залежить від числа Re_D і збільшується зі збільшенням числа Рейнольдса. При Re_D =10⁵/п =1/7. При степеневому розподілі швидкостей (6.424) формула для середньої витратної швидкості запишеться наступним чином:

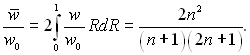
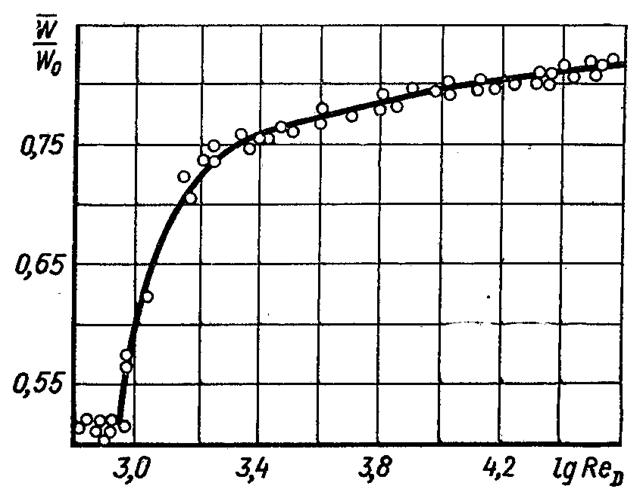
Рис.6.54. Залежність w(/w₀ від числа Рейнольдса: дослідні дані і розраховані за (6.424)

На рис.6.54 наведена залежність w(/w₀ від числа Re_D. Як видно з графіка, що зі збільшенням числа Re_D профіль швидкостей стає все більш заповненим і при Re_D = 10⁸, w(/w₀ = 0,9. Можна показати, що закон опору Блазіуса (6.423) відповідає степеневому розподілу швидкостей з п = 1/7. Підставивши у формулу (6.421) значення ξ  з формули (6.423), отримаємо

(6.425)

Введемо параметр тертя і приймаючи w(/w₀ = 0,8, що відповідає Re_D = 10⁵ і п = 7, отримаємо

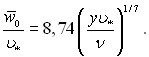(6.426)

Співвідношення (6.426) повинно бути справедливим для будь-якої відстані від стінки, тоді

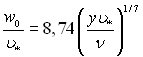(6.427)

і єсть степеневий закон розподілу швидкостей.

При змінних φ і η  цей закон має вигляд

(6.428)

Аналогічний результат отриманий при аналізі турбулентного шару на плоскій пластині. Формула (6.428), узагальнена на довільне число Рейнольдса, має вид:

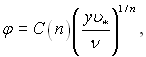(6.429)

де коефіцієнт С залежить від п:

Універсальний закон розподілу швидкостей при турбулентній течії рідини в трубі можна отримати, використовуючи напівемпіричну теорію турбулентності Прандтля. Цей закон, як було показано в § 6.3, має вид

(6.430)

Середня швидкість при турбулентній течії рідини в трубі визначається за формулою:

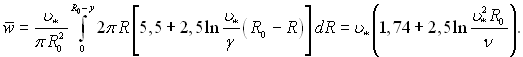(6.431)

Враховуючи, що

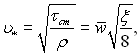(6.432)

отримаємо логарифмічний закон опору при турбулентній течії рідини в трубі

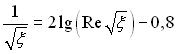. (6.433)

З рис.6.53 видно, що логарифмічний закон опору знаходиться в задовільній відповідності з дослідними даними у всьому діапазоні змін числа Рейнольдса.

Гідравлічний опір шорстких труб практично оказується таким самим, як і для гладких труб, поки товщина в’язкого підшару залишається більшою за виступами поверхні. У випадку коли вони співрозмірні, в підшару виникають збурення, які можуть руйнувати в’язкий підшар. У цьому випадку турбулентні дотичні напруги передаються на стінку труби через напруги тиску на нерівностях профілю і коефіцієнт опору перестає залежати від числа Рейнольдса.

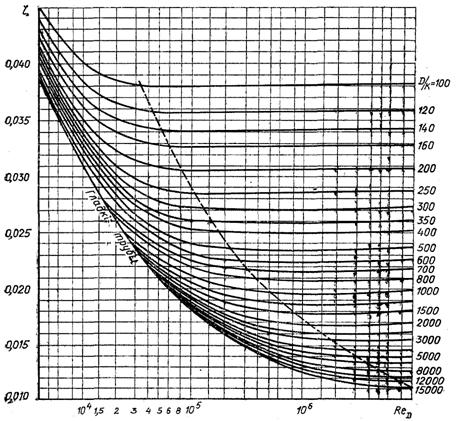
Рис.6.55. Коефіцієнт опору тертя технічних стальних труб

На рис.6.55 наводяться дані по коефіцієнтам гідравлічного опору під час руху рідини в технічних стальних трубах.

Для розрахунку конвективного теплообміну при турбулентній течії рідини в трубах необхідно мати розподіл швидкостей за радіусом труби.

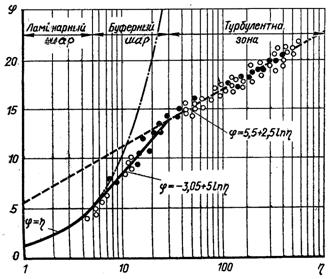
Рис.6.56. Розподіл швидкостей при турбулентній течії рідини в трубах

На рис. 6.56 наводиться співставлення логарифмічного профілю швидкостей (6.430) з дослідними даними. Як видно з графіка, поблизу стінки стверджується лінійний профіль, який в універсальних змінних має вид

                                                           φ = η. (6.434)

При значеннях η > 30 з достатньою точністю підтверджується логарифмічний профіль (6.430). У проміжній області (5 < η  < 30) дослідні дані узагальнюються залежністю

(6.435)

Розрахунки теплообміну з використанням співвідношень (6.434), (6.435) і (6.430) дають надійні результати для області Pr < 20. При великих значеннях чисел Прандтля трьохшарова схема потоку стає незадовільною і приходиться застосовувати більш складні профілі швидкостей, наприклад

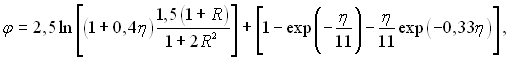(6.436)

де R = r/r₀.

Формула Рейхарда (6.436) описує єдиною залежністю весь профіль швидкостей від стінки до осі потоку.

Конвективний теплообмін в області стабілізованої турбулентної течії рідини в круглій трубі. Розглянемо задачу про течію рідини в круглій трубі за наступних умов 1) густина теплового потоку постійна по довжині труби (q = const); 2) течія і теплообмін квазістаціонарні, тобто осереднені параметри не змінюються в часі; 3) рідина нестислива, а її фізичні властивості постійні; 4) течія гідродинамічно стабілізована, тобто w_x = f(R) і w_r = 0 і теплові пограничні шари зімкнулися; 5) зміна густини теплового потоку вздовж осі нескінченно мала в порівнянні з її зміною по радіусу; 6) внутрішні джерела теплоти відсутні (q_V = 0), а надходження теплоти, викликане дисипацією кінетичної енергії, нескінченно мале.

Для даних умов рівняння енергії має вид

(6.437)

де

(6.438)

Зміну середньо масової температури рідини за довжиною труби знаходимо з рівняння теплового балансу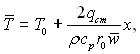

звідки

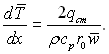(6.439)

Розв’язок рівняння (6.437) будемо шукати в такому виді:

(6.440)

Підставляючи рівняння (6.440) в (6.437), отримаємо

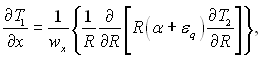
тому що ліва частина цього рівняння залежить тільки від х, а права – тільки від R, що можливе тільки в тому випадку, коли

У відповідності з (6.439) маємо

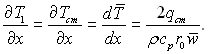(6.441)

Таким чином, при стабілізованому теплообміні у випадку q_ст = const температура на будь-якій відстані від стінки труби, у тому числі і на стінці, змінюється за лінійним законом по довжині труби. Підставляючи дТ/дх з рівняння (6.441) в рівняння (6.437), отримаємо звичайне диференціальне рівняння

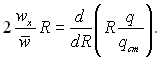(6.442)

Інтегруючи це рівняння за умови q = 0, коли R = 0, отримуємо

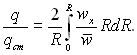. (6.443)

З урахуванням рівняння (6.438) маємо

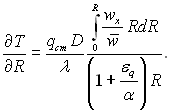(6.444)

Інтегруючи в межах від 1 до R, отримаємо

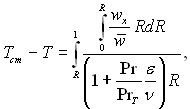(6.445)

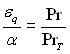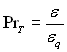де  і  – турбулентне число Прандтля.

Визначимо коефіцієнт тепловіддачі за формулою

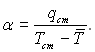
По визначенню,

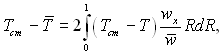(6.446)

підставляючи в це рівняння (Т_ст – Т) з рівняння (6.445), отримаємо

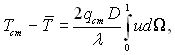(6.447)

де

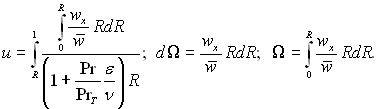
Проінтегруємо рівняння (6.447) по частинах, отримаємо

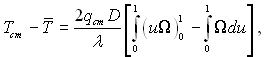
чи

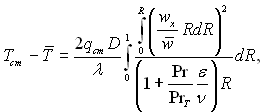(6.448)

звідки

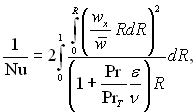(6.449)

Рівняння (6.449) отримано Лайоном і носить назву рівняння Лайона.

В основній частині – ядрі турбулентного потоку, профіль швидкостей суттєво заповнений і в першому наближенні можна вважати, що w/w( = 1.Тоді

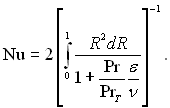(6.450)

Використаємо цю формулу для розрахунку тепловіддачі під час течії рідини з великими значеннями чисел Pr. З дослідів відомо що для середовищ з числами Pr ≈ 1,≈тне число Pr ≈ 1 біля стінки, де має місце найбільш значна зміна температури. У цьому випадку потік рідини в трубі можна умовно розділити на три області: турбулентне ядро, де визначається тільки турбулентним перемішуванням (дією інерційних сил), проміжний шар де молекулярне і турбулентне тертя співрозмірні; в’язкий шар, де вирішальним є молекулярне (в’язкісне) тертя. Досліди показують, що товщина в’язкого підшару мала і в його межах можна вважати ξ³ = 1. Товщина проміжного шару трохи перевищує товщину в’язкого підшару.

Таким чином для Pr ≥ 1 з формули (6.450) виходить, що

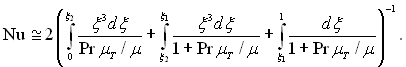(6.451)

Для кожної з розглядуваних трьох областей потоку маємо наступні розрахункові співвідношення:

1) для турбулентного ядра

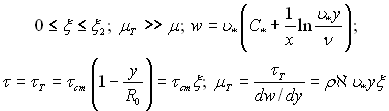
і з урахуванням (6.432)

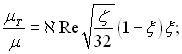
2) для проміжного шару

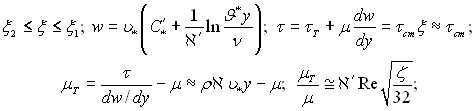
3) для в’язкого підшару

Розрахуємо кожен інтеграл рівняння (6.451) з урахуванням того, що 

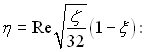
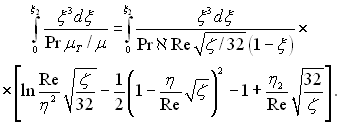
При Re > 104 з точністю до 2%

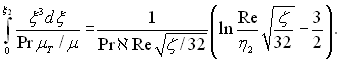(6.452)

Далі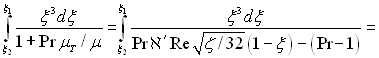

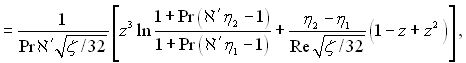
де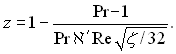

При Re > 104 з точністю до 1%

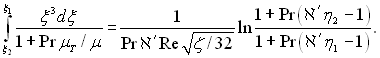(6.453)

Покладаючи η₂ = 30 і η₁  = 6, знаходимо, що א′ = 0,2.

Підставляючи значення інтегралів у (6.451), отримаємо

(6.454)

де

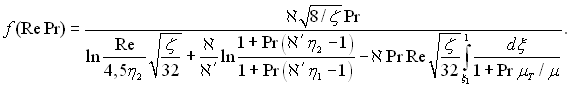
При

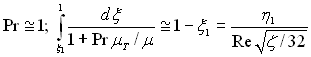(6.455)

і після підстановки числових значень  א, א′, η₁ і η₂ знаходимо

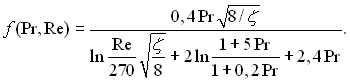(6.456)

Для середовищ з числами Прандтля Pr = 1, f(Pr, Re) = 1. Значення f(Pr, Re) для деяких випадків наведені в табл.6.14.

Таблиця 6.14.Вплив чисел Прандтля і Рейнольдса на теплообмін

Вважаючи у в’язкому підшарі 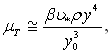отримаємо

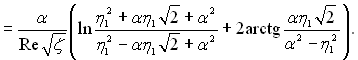(6.457)

де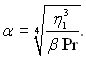

Підставимо цей вираз в (6.456):

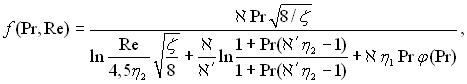
далі введемо числові значення  א, א′, η₁ і η₂:

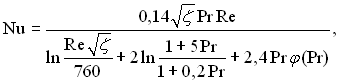(6.458)

де

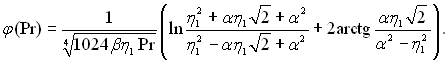(6.459)

При помірних значеннях числа Pr турбулентна теплопровідність у проміжному шарі порівняно невелика і можна використовувати двошарову схему турбулентного потоку. Для цього випадку при η₁ = 11,6 = η₂ і φ(Pr)  1

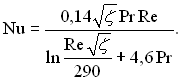(6.460)

Цією формулою можна користуватися для газів і неметалевих рідин при Pr < 5.

При Pr → ∞

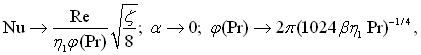(6.461)

отже

(6.462)

Практично формулу (6.462) можна використовувати при Pr > 100.

З урахуванням залежності (6.433)

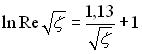
формула (6.458) може бути представлена в наступному виді

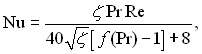(6.463)

де  (6.464)

при цьому f(1) = 1.

Якщо у формулі (6.449) використати профілі швидкостей передбачених (6.335), то результати розрахунків надійно узагальнюються наступними формулами:

для 0,7 < Pr < 200 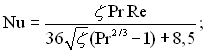(6.465)

для 0,5 < Pr < 200 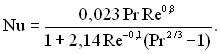 (6.466)

В області 0,5 < Pr < 2,5 задовільні результати дає формула

 (6.467)

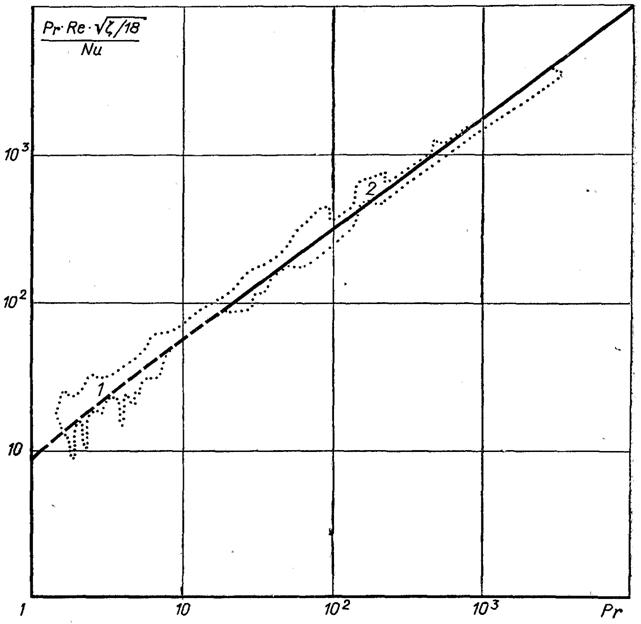
Рис.6.57. Вплив числа Прандтля на турбулентний конвективний теплообмін: ––––– – розрахунок 1– за формулою (6.466); 2 – за формулою (6.461);...........– область дослідних даних

На рис.6.57 співставленні дослідні дані з розрахунковими залежностями. З рисунка слідує, що для інженерних розрахунків конвективного теплообміну під час руху неметалевих рідин можна рекомендувати формулу (6.466) для Pr < 200 і формулу (6.461) для Pr > 200. Для газів і інших середовищ з Pr << 1 можна використовувати формулу (6.460).

Для теплоносіїв з Pr << 1 молекулярні процеси теплопровідності стають суттєвими і в турбулентній частині пограничного шару. Розплавлені метали мають Прандтля порядку 10^–2 і менше. Сильно іонізовані гази мають Pr << 1. Для цих середовищ навіть на зовнішній границі перехідного шару інтенсивність турбулентного переносу теплоти суттєво менше молекулярної теплопровідності. Для цього випадку можна обмежитися двошаровою схемою турбулентного потоку і записати рівняння (6.450) в такому виді:

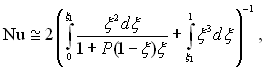(6.468)

де

У граничному випадку при Pr = 0 і q_ст = const

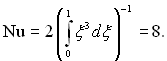(6.469)

Якщо використати більш точну формулу (6.449), підставивши до неї степеневий закон розподілу швидкостей з п =1/7, то отримаємо

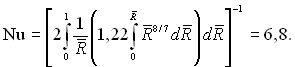(6.470)

Розрахунки для випадку Т_ст = const дають Nu = 5,2...5,5. Таким чином, у стабілізованому турбулентному потоці при Pr → 0 число Нуссельта прямує до постійного значення.

Для інженерних розрахунків тепловіддачі до рідких металів можна рекомендувати наступну формулу:

(6.471)

яка добре узагальнює дослідні дані в діапазоні 10² < Pe < 10⁴ і 10⁴ < Re < 5·10⁴.

Теплообмін і опір під час турбулентної течії в трубах рідини зі змінними фізичними властивостями. Розглянемо конвективний теплообмін при турбулентній течії нестисливої рідини в круглій трубі за попередніх умов, при виключенні допущення сталості фізичних параметрів. У цьому випадку вихідна система диференціальних рівнянь має вид

(6.472)

(6.473)

де h – ентальпія; а ρ, с_р, μ, λ – задані функції температури.

Аналітичні залежності для розглядуваної задачі мають наступний вид:

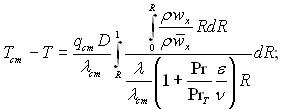(6.474)

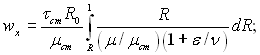(6.475)

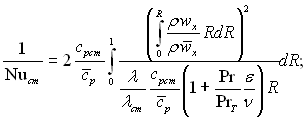(6.476)

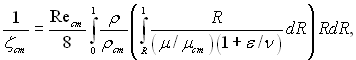(6.477)

де

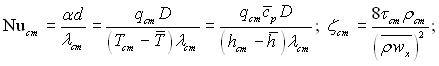
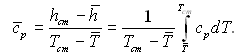
При постійних значеннях фізичних властивостей система рівнянь (6.474)...(6.477) зводиться до відповідних рівнянь при сталих властивостях, отриманих раніше.

Система рівнянь (6.474)...(6.477) розв’язується числовими методами з використанням ЕОМ і кінцеві результати залежать в основному від того, які формули приймаються для коефіцієнтів турбулентного переносу (ε/ν). Тому що всі ці формули мають напівемпіричний характер і питання про вплив змінних властивостей на закони турбулентного переносу є недостатньо вивченим, результати розрахунків необхідно порівнювати з дослідними даними.

Для випадку течії крапельних рідин основний вплив на величину числа Нуссельта чинить змінна в’язкість рідини. Хороше погодження з дослідними даними дає формула

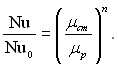(6.478)

При нагріванні рідини μ_ст/μ_р  < 1, п = –0,11; при охолодженні μ_ст/μ_р  > 1, п = 0,25. Число Nu₀ розраховується за формулою (6.465), при цьому фізичні параметри рідини вибираються за середньою температурою в даному перерізі труби. Рівняння (6.478) справедливе в межах зміни відношення μ_ст/μ_р  від 0,08 до 40, Re від 10⁴ до 1,25·10⁵ і Pr від 2 до 140.

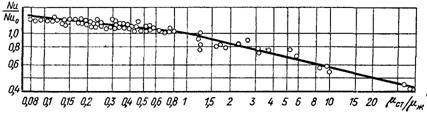
Рис.6.58. Вплив змінної в’язкості на тепловіддачу при турбулентному русі рідини: співставлення дослідних – точки і розрахункових за (6.478) – суцільна лінія

На рис.6.58 порівнюються дослідні дані з розрахованими за формулою (6.478). Під час руху газів в області параметрів стану далеких від кривої насичення, газ можна розглядати як ідеальний. У цьому випадку густина газу пов’язана з тиском і температурою через рівняння Клапейрона-Менделєєва ρ=р/RT. Як показано в розділі 4, інші фізичні параметри газу залежать від температури, і ці залежності можна представити в наступному виді:

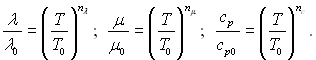
де λ₀, μ₀, с_р0  – значення фізичних параметрів при певній температурі Т₀; п_λ, п_μ,  п_с – сталі, які залежать від природи газу і інтервалу температур.

Таким чином, вплив на теплообмін змінних фізичних параметрів газу проявляється через зміну температури в перерізі пограничного шару.

Якщо використати аналогію між зовнішньою і внутрішньою задачею і записати число Стентора для стабілізованої течії газу в трубі

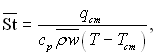
то у випадку зовнішньої задачі число Стентора визначається за параметрами на зовнішній межі пограничного шару. Відповідно число Стентора St₀ для труби параметри на осі труби зв’язані з числом таким співвідношенням:

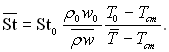 (6.479)

Приймаючи припущення про подібність розподілу швидкостей надлишковим температурам за радіусом труби, тобто

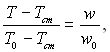
отримаємо, що

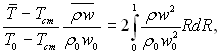(6.480)

де

При степеневому законі розподілу швидкостей і з урахуванням рівняння Клапейрона-Менделєєва маємо

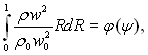(6.481)

де – температурний фактор.

Введемо безрозмірні параметри:

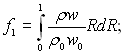(6.482)

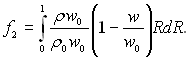(6.483)

Тоді з рівнянь (6.482) і (6.483) матимемо

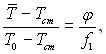(6.484)

звідки отримаємо зв’язок між і . З іншого боку, для числа

St₀ з урахуванням (6.241) можна записати

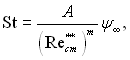(6.485)

де

Тому що

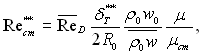(6.486)

де , з урахуванням (6.482), (6.483) і (6.467) отримаємо

(6.487)

На рис.6.59 наводиться порівняння дослідних даних з формулою (6.487).

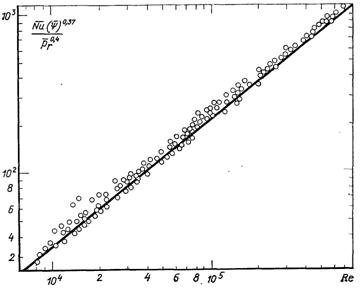
Рис.6.59. Вплив неізотермічності на коефіцієнт тепловіддачі при стабілізованій течії газу в циліндричній трубі. Апроксимація дослідних даних формулою (6.487)

Особливе місце в теорії конвективного теплообміну займають процеси, які відбуваються при тисках більших критичного і температурах не далеких від критичної чи псевдо критичної (температурі, що відповідає точці максимуму теплоємності при сталому тиску). Цікавість до цієї проблеми, особливо у теплоенергетиці, пов’язана з розробкою ядерних реакторів і створення котлоагрегатів, в яких теплоносієм є вода з надкритичними параметрами.

Фізичні властивості речовини біля критичної області суттєвим чином залежить від температури і тиску, що призводить до значних труднощів при узагальненні дослідних даних з теплообміну. На цей час є достатньо велика кількість експериментальних робіт з тепловіддачі в області біля критичної точки, але не існує надійних загальних методів розрахунку за цих умов. Для “газової” області, коли мінімальна температура в пограничному шарі перевищує псевдо критичну, задовільні результати дає наступна формула:

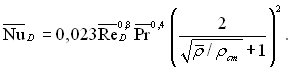(6.488)

З точністю ±20% дослідні дані по воді і двоокису вуглецю узагальнює наступна емпірична формула

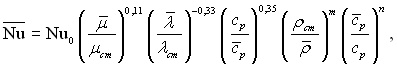(6.489)

де Nu₀ визначається за формулою (6.465); с(_р = (h_ст – h_p)/(Т_ст – Т() – середньо інтегральна теплоємність рідини в інтервалі температур від Т( до Т_ст.

Для води при 1,02≤ р/р_кр ≤ 1,45 т = 0,3; для двоокису вуглецю при 1,02 ≤ р/р_кр ≤ 5,3 т = 0,35 – 0,05р/р_кр. Показник степеня п залежить від Т_ст/Т_т і Т(/Т_т (рис6.60). Формула справедлива при нагріванні рідин з q_ст = const в діапазоні 2·10⁴ ≤ ≤ 8·10⁵; 0,85 ≤ Pr ≤ 5,5; 0,09 ≤ ρ_ст/ρ ≤ 1; 0,02 ≤ с_р/сÐ_р ≤ 4.

 

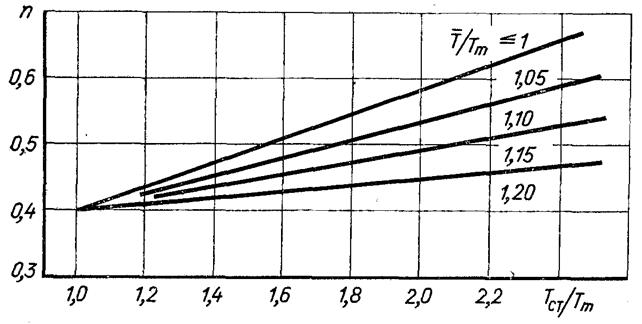
Рис.6.60. Залежність показника степеня п в рівнянні (6.489) від температури

При течії рідини в трубах в області біля критичної точки можуть виникати так названі “погіршенні” режими тепло-віддачі, які супроводжуються появою досить різких сплесків температури гріючої стінки. Механізм виникнення “погіршених” режимів не достатньо вивчений і пов’язується з впливом архімедових сил і прискорень потоку на інтенсивність турбулентного переносу теплоти.

Вплив шорсткості поверхні на теплообмін при турбулентній течії рідини в трубах не круглого поперечного перерізу. Під шорсткою поверхнею розуміють таку поверхню, у якій розміри нерівностей поверхні значно менші товщини пограничного шару чи радіуса труби (при стабілізованій течії). У цьому випадку шорсткість поверхні чинить безпосередній вплив тільки на течію рідини у в’язкому і перехідному шарах. У різних “турбулізаторах” (спеціальні ребра, вставки, шнеки та ін.) виникають подразнення всього потоку.

Розрізняють природну обумовлену технологією виготовлення труб і умовами їх експлуатації, і штучну, тобто спеціально створювану на поверхні труби (різьби, поперечні виступи і канавки, бугорки та ін.) У загальному випадку шорсткість поверхні характеризується висотою і кроком нерівностей профілю. В інженерних розрахунках для оцінки шорсткості поверхні використовують поняття “висота еквівалентної шорсткості” К_е. Під К_е розуміємо таку фіктивну висоту шорсткості, за якої труба з цією шорсткістю має те саме значення коефіцієнта гідравлічного опору, що і труба з дійсним видом шорсткості. Для штучної шорсткості, виконаної із зерен піску однакового розміру, закріплених впритул одне до іншого на поверхні труби (піщана шорсткість) К_е = К, де К – еквівалентний діаметр піщинки.

Тепловіддача на шорсткій поверхні більша, ніж на гладкій, що пов’язано зі збільшенням інтенсивності турбулентного переносу в пристінній області. Одночасно з ростом тепловіддачі зростає і гідравлічний опір.

Ефективність шорсткої поверхні можна оцінити за формулою

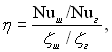 (6.490)

де Nu_ш, Nu_г, ζ_ш, ζ_г – числа Нуссельта і коефіцієнти опору тертя для труб з шорсткою і гладкою поверхнями при одних і тих же значеннях чисел Re і Pr.

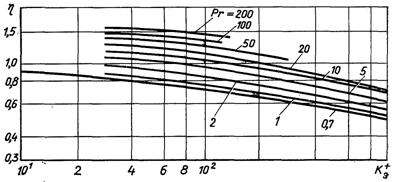
Рис.6.61. Залежність коефіці-єнта ефективності шорсткості труб від К_е⁺ при різних значеннях Pr

На рис.6.61 наведена залежність коефіцієнта ефективності η від параметра шорсткості

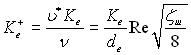
і числа Прандтля. На підставі цього графіка можна розраховувати тепловіддачу на шорсткій поверхні, якщо відомі ζ_ш, ζ_г і К_е.

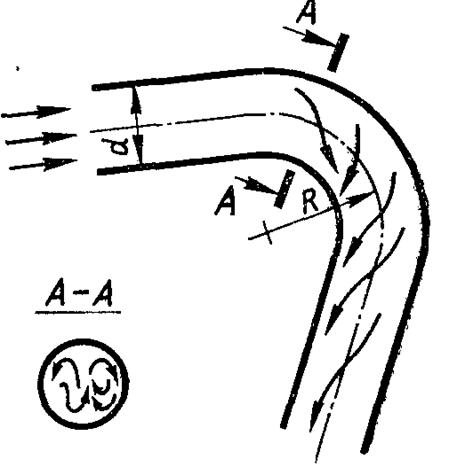
Рис.6.62. Течія в зігнутому каналі

У багатьох практичних випадках рідина тече по трубі, вісь якої є дуга кола. За цих умов виникають відцентрові сили, які призводять до складного руху рідини за гвинтовою лінією (рис.6.62). У наслідок цього місцеві коефіцієнти тепловіддачі на зовнішній стороні дуги кола оказуються далі, ніж внутрішні. Для розглядуваних умов підтверджується аналогія Рейнольдса, тобто

(6.491)

де

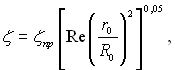(6.492)

r₀ – радіус труби; R₀ – радіус гину осі труби; ζ_пр– коефіцієнт гідравлічного опору для прямої труби, який визначається за формулою (6.423). Формула (6.492) справедлива при Rer₀/R₀ > 6.

Розрахунок тепловіддачі в трубах не круглого поперечного перерізу при турбулентній течії рідини в деяких випадках можна виконувати за формулами, отриманими для круглих труб [формули (6.465), (6.467)], якщо за характерний лінійний розмір в числах подібності Nu і Re використовувати еквівалентний діаметр

(6.493)

де f – площа поперечного перерізу каналу; Р – змочений периметр поперечного перерізу каналу незалежно від того, яка його частина обмінюється теплотою з рідиною.

Метод розрахунку тепловіддачі з використанням d_е є наближеним, особливо при малих числах Прандтля. Для отримання більш точних результатів використовують рівняння подібності теплообміну, отримане для даного профілю прохідного перерізу каналу. Так, наприклад, при течії крапельних рідин в каналах кільцевого поперечного перерізу середні коефіцієнти тепловіддачі для поверхні внутрішньої труби можна визначати за формулою

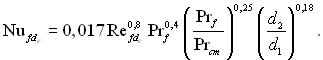(6.494)

У цьому рівнянні визначальною є середня температура рідини в трубі і d_e = d₂ – d₁, де d₁ – внутрішній діаметр кільцевого каналу; d₂ – зовнішній діаметр. Формула (6.494) справедлива при d₂ /d₁ = 1,2...1,4; ℓ/d = 50...460; Pr_f = 0,7...100. Під час течії рідини в трикутних каналах виникають крупно масштабні вихрові течії, які суттєво ускладнюють процес теплообміну.

Теплообмін при турбулентній течії рідини на початковій ділянці труби. Перехід від ламінарного режиму течії у пограничному шарі до турбулентного на початковій ділянці труби відбувається так само, як і на плоскій пластині. Якщо турбулентний пограничний шар починає зростати від початкового перерізу труби, то розрахунок розвитку динамічного і теплового пограничного шару на початковій ділянці труби виконують за формулами отриманими в § 6.3 для зовнішнього обтікання тіл. Різниця криється в тому, що при зовнішньому обтіканні тіл швидкість рідини на зовнішній границі пограничного шару є заданою величиною, а для розглядуваних умов для початкової ділянки труби вона є шуканим параметром. Для її визначення вводиться додаткове рівняння сталості витрат рідни по довжині труби.

Розглянемо течію рідини на початковій ділянці циліндричної труби при рівномірному розподілі швидкості і температури на вході в трубу. У цьому випадку рівняння нерозривності потоку можна записати так

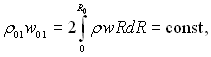(6.495)

де ρ₀₁ і w₀₁ – густина і швидкість рідини в початковому перерізі труби.

Товщина витіснення для циліндричної труби визначається формулою

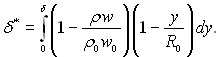(6.496)

Тоді рівняння (6.495) набуде наступного виду

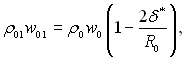(6.497)

де ρ₀ і w₀ – густина і швидкість рідини в ядрі потоку, де течія розглядається як потенціальна.

Для випадку постійності густини турбулентного пограничного шару формпараметр Н = δ^*/δ^** = 1,3. Тоді з рівняння (6.497) маємо

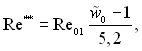(6.498)

де

Інтегральне співвідношення імпульсів (6.59), закон тертя (6.233) і рівняння (6.498) утворюють замкнену систему рівнянь, аналітичний розв’язок якої при т = 0,25 і В = 0,0256 має вид

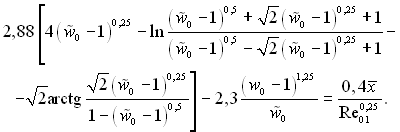(6.499)

Знаючи залежність w̃₀ від х, за формулою (6.498) визначаємо локальні значення Re^** і з рівняння (6.233) – коефіцієнт тертя

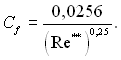(6.500)

Довжина початкової ділянки визначається з умови перетину пограничних шарів. У цьому випадку δ =R₀ δ^*/R₀ = 0,097. Тоді з рівняння (6.497) виходить

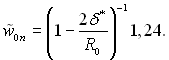(6.501)

Рівняння (6.500) з достатньою точністю можна апроксимувати простою залежністю

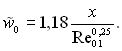(6.502)

Тоді з урахуванням (6.501) отримаємо формулу для довжини початкової ділянки

(6.503)

У випадку течії газу з дозвуковими швидкостями на вході, але за умови суттєвої неізотермічності, формула (6.503) набуває виду

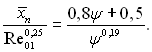(6.504)

Для визначення локальних значень коефіцієнтів тепловіддачі проінтегруємо інтегральне співвідношення енергії при законі зміни швидкості на зовнішній границі, що визначається формулою (6.502). З рівняння (6.63) маємо

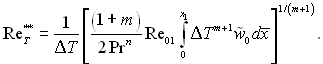(6.505)

З урахуванням (6.502) для випадку Т_ст = const отримаємо за умови, що

т = 0,25 і В/2 = 0,0128: (6.506)

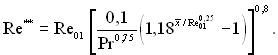(6.507)

Використовуючи закон теплообміну (6.241), отримаємо

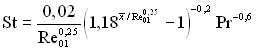(6.508)

чи

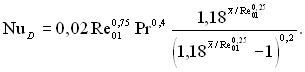(6.509)

Ця формула дозволяє розрахувати локальні значення коефіцієнтів тепловіддачі на початковій ділянці труби при одночасному розвитку динамічного і теплового пограничних шарів при постійній температурі стінки.

Однак, використовуючи рівняння (6.505), можна отримати розрахункове рівняння для будь-якого закону зміни температури стінки за довжиною труби. В окремому випадку, для q_cm = const з рівняння (6.60) маємо

З урахуванням закону теплообміну отримаємо