




6.5.1. Теплообмін при вимушеному ламінарному русі рідини в трубах
Ізотермічна течія. Розглянемо ламінарний рух рідини з постійними фізичними властивостями в умовах гідродинамічної стабілізації.
Для випадку руху рідини в круглій трубі в області стабілізованої течії рівняння руху набуває вигляд
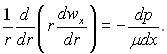 (6.325)
(6.325)
Після подвійного інтегрування отримуємо
![]() (6.326)
(6.326)
Використовуючи граничні умови у вигляді: при ![]() при r = r0 wx=0, знаходимо С1 = 0 і
при r = r0 wx=0, знаходимо С1 = 0 і 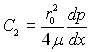 , при цьому розподіл швидкостей за перерізом отримуємо у вигляді параболи:
, при цьому розподіл швидкостей за перерізом отримуємо у вигляді параболи:
![]() (6.327)
(6.327)
Середня витратна швидкість
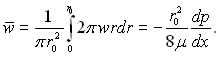 (6.328)
(6.328)
Підставляючи значення dp/dx з (6.328) і (6.327), отримаємо
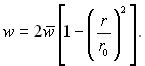 (6.329)
(6.329)
Таким чином, при ламінарному русі швидкість на осі труби у двічі більша середньої швидкості.
Рівняння (6.325) можна записати у вигляді
![]() (6.330)
(6.330)
Якщо під τ розуміти сумарну дотичну напругу (τ = τл + τт), то рівняння (6.330) справедливе як для ламінарного, так і для турбулентного режиму руху рідини.
Тому що при стабілізованому русі рідини з постійними фізичними властивостями dp/dx = const, то з рівняння (6.330) виходить, що
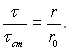 (6.331)
(6.331)
У гідравліці втрати тиску на одиницю довжини виражаються формулою
![]() (6.332)
(6.332)
де ζ – коефіцієнт гідравлічного опору.
Підставляючи в (6.332) значення (–dp/dx) з (6.328), знаходимо що при ламінарному режимі руху в круглій трубі
ζ = 64/ Re (6.333)
де Re = w(d/ν.
Зараз відомі профілі швидкостей за ламінарного усталеного руху рідини в каналах з самими різними формами живого перерізу (табл.6.9).
Таблиця 6.9. Рівняння профілів швидкостей в трубах різного живого перерізу при ламінарному режимі руху
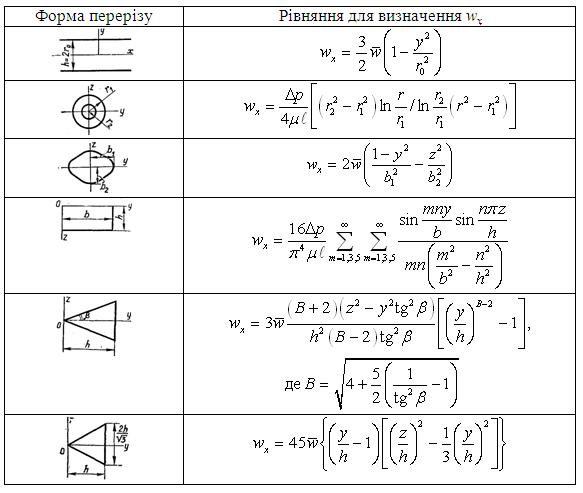
Вихідне диференціальне рівняння для аналізу цієї задачі отримують з рівняння Нав’є-Стокса. Для усталеного ламінарного руху (в напрямку х) рідини з постійними фізичними властивостями і при відсутності масових сил це рівняння набуває вигляду:
![]()
Якщо вважати, що похідна dp/dx стала в живому перерізі, то рівняння можна розв’язати різними методами, наприклад числовим. Але якщо визначити середню по периметру дотичну напругу і використати її для розрахунку зменшення тиску, то коефіцієнт тертя можна розрахувати за рівнянням:
![]()
Для труб з перерізом у вигляді рівностороннього трикутника справедлива залежність
CfRe = 13,33.
Число Re визначається за гідравлічним радіусом труби r0. Під час руху рідини по зігнутим трубам зазвичай виникають вторинні течії, які значно ускладнюють процес переносу імпульсу. Для стабілізованої ламінарної течії в круглій трубі, вісь якої представляє собою дугу кола радіусом R, пропонується наступне рівняння для коефіцієнта тертя:
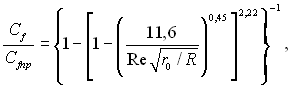 (6.334)
(6.334)
справедливе при 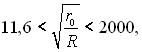 де Cf – коефіцієнт тертя в зігнутій трубі; Cfпр– коефіцієнт тертя в прямій трубі.
де Cf – коефіцієнт тертя в зігнутій трубі; Cfпр– коефіцієнт тертя в прямій трубі.
Теплообмін в циліндричній трубі при гідравлічно стабілізованій течії. Розглянемо ламінарний стабілізований рух рідини в круглій трубі при постійній температурі стінки за довжиною труби. Відомі величини: витрати рідини, температура стінки tcm і температура рідини на вході в трубу. При такій постановці задача була розв’язана Нуссельтом. Задача розв’язувалася при наступних умовах:
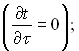
Рівняння енергії для нестисливої рідини з постійними фізичними властивостями при відсутності в потоці джерел теплоти і дисипації енергії в циліндричних координатах має вид:
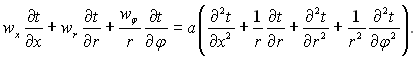 (6.335)
(6.335)
Для стабілізованої ламінарної течії
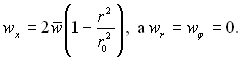
Внаслідок осьової симетрії 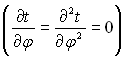 і останньої умови
і останньої умови 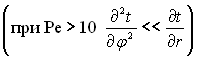 , а також якщо ввести нову змінну J = t – tcm, то отримаємо рівняння енергії в наступному виді:
, а також якщо ввести нову змінну J = t – tcm, то отримаємо рівняння енергії в наступному виді:
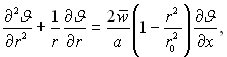
чи в безрозмірному виді
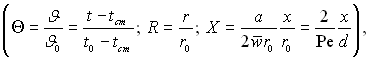
![]() (6.336)
(6.336)
при Х = 0 і 0 ≤ R < 1 Θ = 1; (6.337)
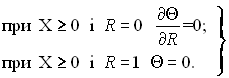 (6.338)
(6.338)
Рішення диференціального рівняння шукаємо у вигляді добутку двох функцій:
![]() (6.339)
(6.339)
Підставляючи (6.339) в рівняння (6.336), отримаємо
![]()
Розділивши змінні, отримаємо два звичайні диференціальні рівняння
![]() (6.340)
(6.340)
з рішенням у вигляді
![]() (6.341)
(6.341)
рішення другого рівняння
![]() (6.342)
(6.342)
Нуссельт запропонував шукати у вигляді ряду

підстановка якого в (6.342) дає
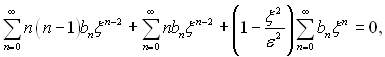
чи
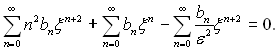
Перетворимо вираз так, щоб показники степеня біля ξ у всіх членах були одного значення k:
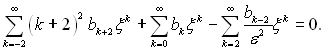
Надамо цьому рівнянню іншого вигляду:
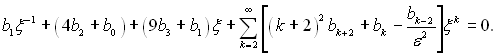
У зв'язку з тим, що рівняння повинно виконуватися за довільних ξ, то коефіцієнти біля членів з ξ у різних степенях повинні дорівнювати нулю, тобто
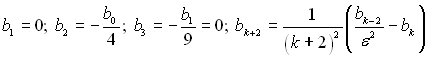
для k ≥ 2, при цьому коефіцієнти біля парних членів виражаються через два попередніх парних коефіцієнтів, а при непарних – відповідно через два непарних коефіцієнта. Рішення ψ(R) можна подати у вигляді ряду, який містить у собі εR тільки в парних степенях:
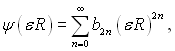 (6.343)
(6.343)
де умовно приймаємо b0 = 1 (n = 0);
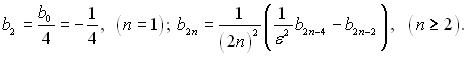
У розгорненому вигляді можна записати
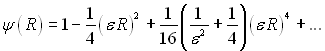 (6.344)
(6.344)
Ряд сходиться при довільних значеннях εR і ε. Постійна ε визначається з граничної умови (6.338) при R = 1 ψ = 0:
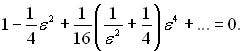 (6.345)
(6.345)
Це рівняння має нескінченну кількість корнів εп, які називаються власними значеннями. Нуссельт розрахував перших три кореня:
ε0 = 2,705; ε1 = 6,66; ε2 = 10,3.
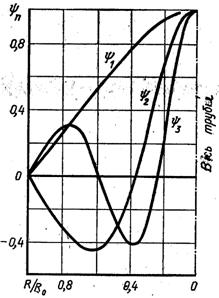
Рис.6.42. Графік функції ψп
Кожному значенню εп відповідає певна функція ψ(εп, Rεп) = ψn(R). Перші три функції для приведених значень εп наведено на рис.6.42.
Окремий розв’язок диференціального рівняння (6.342) можна записати так
![]()
Загальний розв’язок це сума всіх окремих рішень:
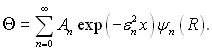 (6.346)
(6.346)
У цьому рівнянні невідомі тільки Ап, які можна знайти з розподілу температури на вході. Так, при х = 0 Θ0(R) = 1 і
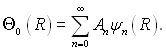 (6.347)
(6.347)
З урахуванням (6.347) розв’язок (6.346) запишеться так:
![]()
Тому що ψп і ψт є рішеннями рівняння, то його можна записати:
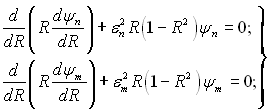 (6.348)
(6.348)
Помножимо перше рівняння на ψт, а друге – на ψп і віднімемо від другого рівняння перше, отримаємо:
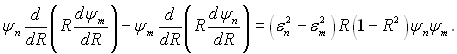
Ліву частину цього рівняння представимо так
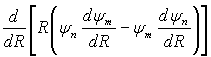
і проінтегруємо її по R в межах від 0 до 1:
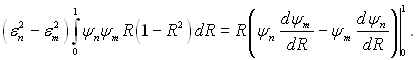 (6.349)
(6.349)
Права частина рівняння перетворюється в нуль при R = 0 і R = 1, тому що
![]()
Звідки слідує властивість ортогональності:
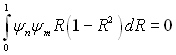
при т ≠ п, яке враховуємо, можна отримати
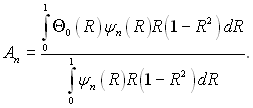 (6.350)
(6.350)
При Θ =1 інтеграл в чисельнику становить
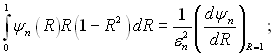 (6.351)
(6.351)
а в знаменнику
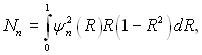
який можна вирахувати, використавши рівняння (6.349).
Вважаючи ε безперервною величиною, яка прямує до εп, матимемо
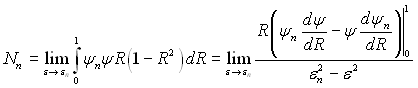
і, розкриваючи невизначеність, отримаємо
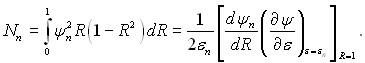 (6.352)
(6.352)
Виходячи з цього
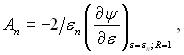 (6.353)
(6.353)
де похідна 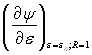 визначається за рівнянням (6.344).
визначається за рівнянням (6.344).
Внаслідок розрахунків отримані наступні значення:
А0 = 1,477; А1 = –0,810; А2 = 0,385.
Кінцевий розподіл температури рідини у потоці визначається за формулою:
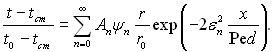 (6.354)
(6.354)
Значення ψп(R), εп і Ап наведені в табл. 6.10 і 6.11
Таблиця 6.10. Значення власних функцій
Таблиця 6.11. Власні значення
п |
εп |
εп2 |
Ап |
Вп |
0 1 2 3 4 5 6 7 8 9 10 |
2,704364 6,679031 10,673380 14,671078 18,669872 22,669143 26,668662 30,668323 34,668074 38,667883 42,667734 |
7,313586 44,60946 113,92104 215,24053 348,56412 513,89004 711,21753 940,54604 1201,8754 1495,2052 1820,5355 |
+1,4764354 –0,8061239 +0,5887621 –0,4758504 +0,4050218 –0,3557565 +0,3191690 –0,2907358 +0,2678911 –0,2490625 +0,2332277 |
0,74877450 0,54382795 0,46286100 0,41541840 0,38291915 0,35868555 0,33962210 0,32406215 0,31101395 0,29984400 0,29012455 |
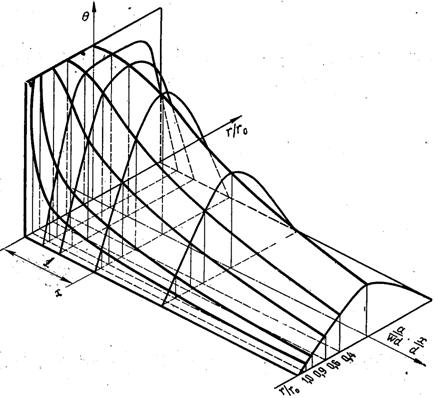
Рис.6.43. Розподіл температур в трубі за Нуссельтом: 1 – вхідна ділянка
На рис.6.43 наводиться розподіл температури по радіусу і довжині труби [розрахунок виконаний за рівнянням (6.354)]. Розрахунок для великих значень п складний, і у таких випадках використовують асимптотичний розв’язок, який дозволяє значно спростити розрахунок:
![]() (6.355)
(6.355)
![]() (6.356)
(6.356)
Для малих значень R (біля осі труби)
![]() (6.357)
(6.357)
Для середніх значень R
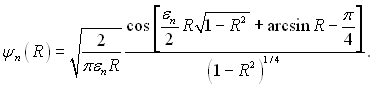 (6.358)
(6.358)
Для R в межах одиниці (біля стінки),
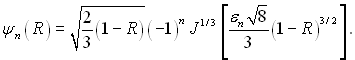 (6.359)
(6.359)
Введемо параметр Вп для R = 1:
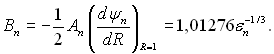 (6.360)
(6.360)
Надійна відповідність точного і асимптотичного рішення спостерігається при п≥3.
При великій приведеній довжині можна залишити тільки перший член ряду:
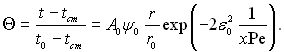 (6.361)
(6.361)
Середня масова температура рідини
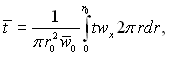
чи у безрозмірній формі запису
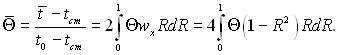
Підставимо вираз (6.361) для Θ в останню формулу, тоді отримаємо
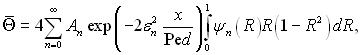
і у кінцевому виді
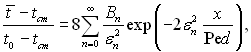 (6.362)
(6.362)
де
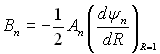 .
.
Локальний коефіцієнт тепловіддачі визначається за формулою
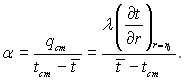
Вводячи число Нуссельта, матимемо:
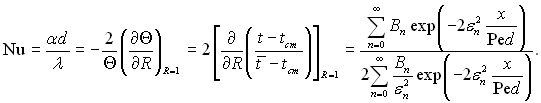 (6.363)
(6.363)
З аналізу формули (6.363) виходить, що
при х → 0 Nu → ∞; при х → ∞ Nu = ε02/2 = 3,657 (6.364)
і α залежить тільки від теплопровідності рідини і діаметра труби. Як видно з рис.6.44, усю довжину назріваючої труби можна розділити на дві ділянки. На першій ділянці відбувається формування профілю температури (число Nu зменшується за довжиною), на другій – закон розподілу температури за
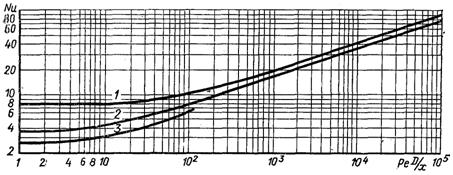
Рис.6.44. Залежність числа Нуссельта від комплексу PeD/x за ламінарної течії: 1 – плоска щілина; 2 – кругла труба; 3 – рівносторонній трикутник
радіусом і не змінний за довжиною (число Nu зберігає постійне значення). Перша ділянка називається термічною початковою ділянкою, а друга – стабілізований теплообмін. Довжину термічної початкової ділянки можна визначити як відстань від вхідного перерізу, де число Nu з точністю 1% приймає постійне значення. З рівняння (6.363)
![]() (6.365)
(6.365)
При заданому числі Re довжина початкової термічної ділянки визначається числом Pr. Для рідко металевих теплоносіїв ℓп.т не перевищує декількох діаметрів, для газів – декількох десятків діаметрів, для крапельних рідин – змінюється від декількох сотень до десятків тисяч діаметрів. Звідси виходить, що в трубах теплообмінних апаратів для рідин з числом Pr > 1 теплообмін при ламінарному режимі руху за всією довжиною труби відбувається в області термічної початкової ділянки. Для практичних розрахунків тепловіддачі використовувати рівняння (6.363) незручно. Розв’язок (6.363) можна спростити, підставивши асимптотичне значення εп, Вп і замінивши суму інтегралом.
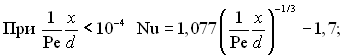 (6.366)
(6.366)
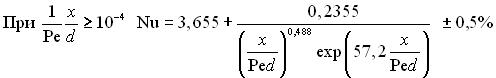 . (6.367)
. (6.367)
Середній інтегральний коефіцієнт тепловіддачі
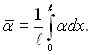
З рівняння теплового балансу для елементу труби довжиною dx маємо
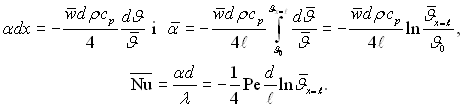
Підставляючи Θ( з рівняння (6.362), отримаємо
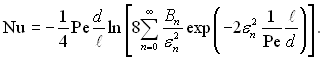 (6.368)
(6.368)
З точністю до 4% при Peℓ/d < 250 можна використовувати інтерполяційне рівняння
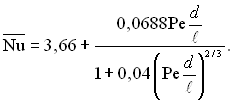 (6.369)
(6.369)
У техніці часто приходиться розв’язувати задачі теплообміну при постійній густині теплового потоку на стінці; до них відносяться електронагрів, радіаційний нагрів, нагрів в ядерних реакторах і в протитечійних теплообмінниках за рівності водяних еквівалентів теплоносіїв. Для таких випадків з рівняння теплового балансу виходить, що
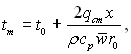 (6.370)
(6.370)
чи у безрозмірній формі запису
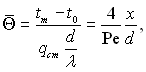 (6.371)
(6.371)
де ![]() t0 – стала температура рідини на вході в трубу.
t0 – стала температура рідини на вході в трубу.
При заданих теплових навантаженнях шуканими є температура стінки і коефіцієнт тепловіддачі. Для цього випадку рівняння енергії має вид
![]() (6.372)
(6.372)
граничні умови
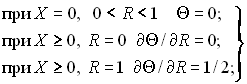 (6.373)
(6.373)
де 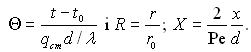
Розглянемо розв’язок цієї задачі для області, віддаленій від входу в трубу, де установився автомодельний профіль температури з постійними за довжиною коефіцієнтами тепловіддачі. У цьому випадку можна вважати, що температура Θ при будь-яких значеннях R змінюються лінійно за довжиною труби, так само як і Θ(, тоді
![]() (6.374)
(6.374)
де А – стала, а f(R) – невідома функція.
Щоб підтвердити прийняте допущення, визначимо А і вид функції f(R), для цього підставимо (6.374) в (6.372):
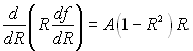
Інтегруючи це рівняння в межах від 0 до R і враховуючи, що при R = 0, df/dR= 0, маємо
df/dR = А(R/2 – R3/4).
З третьої граничної умови (6.373) визначимо А = 2. Повторне інтегрування дає
f(R) = R2/2 – R4/4 + С.
Отже,
Θ = 2Х + R2/2 – R4/8 + С. (6.375)
Сталу інтегрування С знаходимо з рівняння (6.371), попередньо визначивши середню температуру за формулою
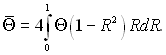 .
.
Після інтегрування і підстановки Θ( в рівняння (6.373) знаходимо, що С = –7/48.
Кінцевий вираз для профілю температури має вид
![]() (6.376)
(6.376)
і, як окремий випадок, температура стінки
![]() (6.377)
(6.377)
Визначимо число Нуссельта для розглядуваних умов:
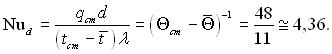 (6.378)
(6.378)
Таким чином, в області, віддаленій від входу в трубу, при постійному питомому тепловому навантаженні температура стінки змінюється за довжиною по лінійному закону, а число Нуссельта зберігає постійне значення. Із співставлення формул (6.378) і (6.364) виходить, що при постійному тепловому навантаженні в області стабілізованої течії число Нуссельта на 19% перевищує своє значення при постійній температурі стінки.
Розглянемо задачу про теплообмін на початковій термічній ділянці при qcm = const за довжиною. Введемо нову змінну
Θ1 = Θ – Θ* (6.379)
де Θ* – окремий розв’язок для області стабілізованого теплообміну, який виконується за рівнянням (6.376).
Задача зводиться до інтегрування рівняння
![]() (6.380)
(6.380)
при граничних умовах
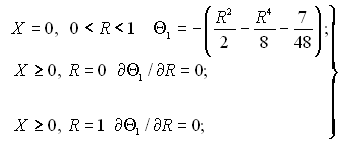 (6.381)
(6.381)
Рішення можна отримати тим же методом, що застосовувалося при граничних умовах при tcm = const. Отже, загальний розв’язок для Θ1 має аналогічний вид:
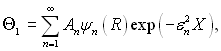 (6.382)
(6.382)
де εп (п =1, 2, 3,...) – власні значення; ψп(R) – власні функції; Ап – постійні коефіцієнти. Кінцевий вираз для розподілу температури
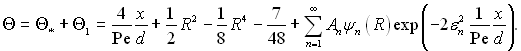 (6.383)
(6.383)
Для температури стінки
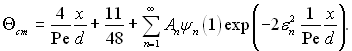 (6.384)
(6.384)
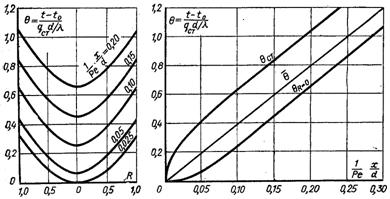
Рис.6.45. Розподіл температури за радіусом і довжино. труби при qст = const
Значення εп2, ψп(1) і Ап наведено в табл.6.10 і 6.11, а на рис.6.45 показаний розподіл температури рідини за радіусом і довжиною труби.
Локальні значення числа Нуссельта визначаються з рівняння (6.384):
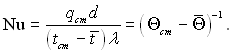
З урахуванням (6.384), маємо
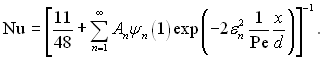 (6.385)
(6.385)
При досить великих значеннях відношення x/d сума членів ряду прямує до нуля і рівняння (6.385) переходить в (6.378), отримане раніше для області стабілізованого теплообміну.
Визначивши довжину початкової теплової ділянки з умови ![]() отримаємо
отримаємо
![]() (6.386)
(6.386)
Таким чином, довжина ділянки теплової стабілізації для умови qcm = const на 27% більше за аналогічну довжину для випадку tcm = const.
Для приведеної довжини ![]() з похибкою ± 4% число Нуссельта визначається за інтерполяційним рівнянням
з похибкою ± 4% число Нуссельта визначається за інтерполяційним рівнянням
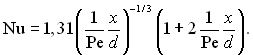 (6.387)
(6.387)
Якщо обігрів труби починається з входу рідини в трубу, де розподіл швидкостей рівномірний, то тепловіддачу можна розрахувати за формулою
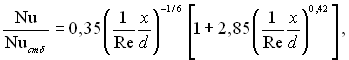 (6.388)
(6.388)
де Nucmδ – місцеве число Нуссельта, яке визначається за формулою (6.385) чи (6.387).
Рівняння (6.388) справедливе при зміні параметрів у межах
![]()
При ![]() профіль швидкостей стає параболічним і Nu = Nucmδ.
профіль швидкостей стає параболічним і Nu = Nucmδ.
Часто зустрічаються випадки, коли густина теплового потоку по колу труби неоднакова, що призводить до перегріву окремих ділянок поверхні. Вихідним рівнянням для цього випадку при сталій густині теплового потоку на стінці за довжиною труби є наступне:
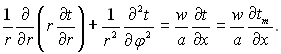 (6.389)
(6.389)
Воно розв’язується методом теплового джерела чи методом суперпозицій.
При косинусоїдальній зміні теплового потоку (багато неоднорідних розподілів густини теплового потоку можна апроксимувати розкладом за косинусом) q = qa(1 + bcosφ) місцеве число Нуссельта можна розраховувати за рівнянням:
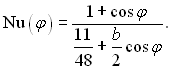 (6.390)
(6.390)
Якщо b = 0, Nu = 4,364. У залежності від значення b число Нуссельта може приймати будь-які значення аж до Nu = ∞. Нескінченний коефіцієнт тепловіддачі означає, що температура стінки дорівнює середньо масовій температурі рідини.
Велику практичну зацікавленість представляє теплообмін в круглій трубі при змінній густині теплового потоку на стінці. У зв'язку з тим, що рівняння енергії (6.372) лінійне, то розв’язок цього рівняння для випадку qcm=const можна розповсюдити на довільний закон зміни qcm за довжиною, використовуючи метод суперпозицій.
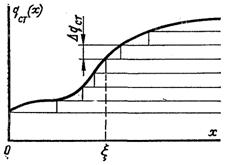
Рис.6.46. До задачі про теплообмін при довільній зміні qcm
Розглядувану задачу qcm = f(x) можна апроксимувати ламаною лінією, при цьому на кожній ділянці Δξ тепловий потік приймається постійним (рис.6.46). Кожна сходинка теплового потоку розвитку температурного поля, описується рівнянням (6.383).
Тому що рівняння енергії (6.372) лінійне відносно температури, то температурне поле в потоці зі східчастим розподілом теплового потоку на стінці можна подати як суму температурних полів від окремих сходинок:
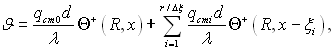
де Θ+ – розв’язок задачі про теплообмін при qcm=const (6.383). Замінивши кінцеві приростання Δqcm на dqcm і переходячи від суми до інтегралу, отримаємо
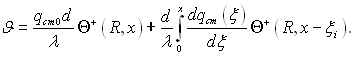
Розділимо це рівняння на середню за довжиною густину теплового потоку:
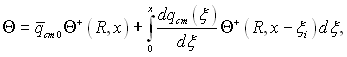 (6.391)
(6.391)
де
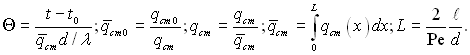
При R = 1 отримаємо рівняння для температури стінки
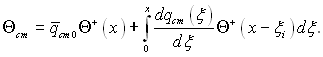 (6.392)
(6.392)
Запишемо вираз для середньо масової температури рідини
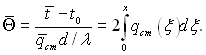 (6.393)
(6.393)
Локальне значення числа Нуссельта визначається за формулою
![]() (6.394)
(6.394)
Розрахунки показують, що локальні значення числа Нуссельта суттєво залежить від закону зміни qcm за довжиною труби. У випадку збільшення qcm число Nu збільшується, а у випадку зменшення qcm – менше, ніж при qcm=const. Доказано, що поведінка числа Nu при х→ ∞ визначається параметром
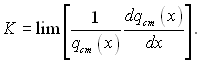
Якщо К має кінцеве значення, відмінне від нуля, то число Нуссельта прямує до певного значення, відмінного від Nu∞ при qcm=const. Якщо ж К = ±∞ (тобто межі не існує), то число Nu необмежено збільшується чи зменшується за довжиною труби.
Велике технічне значення має розрахунок теплообміну в кільцевому каналі. Диференціальне рівняння енергії для кільцевого каналу таке саме, як і для круглої труби (для випадку qcm=const):
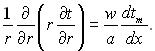 (6.395)
(6.395)
Шляхом інтегрування рівняння руху
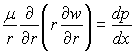
визначимо профіль швидкостей в кільцевому каналі:
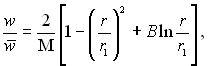 (6.396)
(6.396)
де 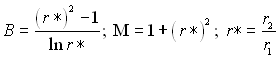 .
.
У цьому разі рівняння енергії набуває вигляду
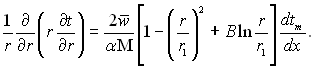 (6.397)
(6.397)
Це рівняння легко інтегрується, а граничні умови визначаються за заданими густинами теплових потоків на стінках каналу. Але немає необхідності розв’язувати рівняння енергії для кожного окремого випадку. Лінійність рівняння енергії дозволяє за допомогою методу суперпозиції знаходити рішення для несиметричного нагрівання каналу шляхом додавання інших рішень при дотриманні граничних умов. Як граничний випадок можна розглянути теплообмін при ламінарній течії між паралельними пластинами, у цьому випадку
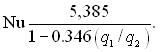 (6.398)
(6.398)
При нагріванні тільки однієї стінки q2 = 0 і Nu = 5,385. При рівних густинах теплових потоків на обох пластинах q2/q1 = 1 і Nu1 = Nu2 = 8,23.
Розв’язок рівняння енергії для труб прямокутного і трикутного перерізу отримують тими ж методами, що і для круглих труб. Вихідне диференціальне рівняння енергії є частинним випадком рівняння
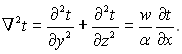
Розподіл швидкостей визначається рішенням рівняння руху
![]()
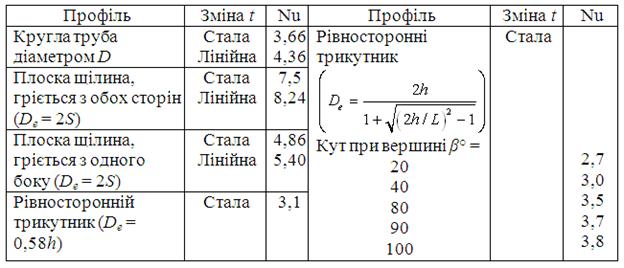
Кінцеві розрахункові формули для чисел Нуссельта в каналах різної форми наведені в табл.6.12 і 6.13.
Таблиця 6.12. Вплив форми каналу на тепловіддачу
Профіль каналу |
Еквівалентний діаметр |
Область чисел PeDe/L |
Число Nu |
Кругла труба діаметром D |
De = D |
>12 <12 |
1,61(PeDe/L)1/2 3,66 |
Плоска щілина шириною S |
De = 2S |
>70 <70 |
1,85(PeDe/L)1/3 7,50 |
Рівносторонній трикутник, ширина сторони якого h |
De = 0,58h |
>7 <7 |
1,5(PeDe/h)1/3 2,70 |
Таблиця 6.13. Вплив форми каналу на тепловіддачу в області
стабілізованої течії
Теплообмін стабілізованої ділянки труби з урахуванням теплоти тертя. Розглянемо стабілізовану ламінарну течію в плоскій щілині. Рухоме середовище вважається нестисливим, а фізичні константи – незалежними від температури.
За цих умов повне рівняння енергії для плоскої стаціонарної течії має вид
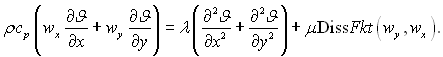
при цьому напрямок х співпадає з напрямком течії, а вісь у нормальна до стінки щілини.
Для стабілізованої течії приймається ![]() у всьому полі
у всьому полі ![]() що веде до зникнення також похідних
що веде до зникнення також похідних ![]() , і дисипативна функція Diss спрощується до виразу
, і дисипативна функція Diss спрощується до виразу ![]() Крім цього, тут wx=w, отже, для розглядуваних умов рівняння енергії перетворюється до виду
Крім цього, тут wx=w, отже, для розглядуваних умов рівняння енергії перетворюється до виду
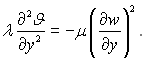 (6.399)
(6.399)
Для швидкості приймається розподіл
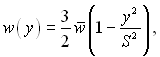 (6.400)
(6.400)
де ширину щілини приймають рівною 2S.
Розглядаючи сумісно рівняння (6.399) і (6.400), отримаємо
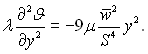 (6.401)
(6.401)
Якщо стінки щілини мають різну температуру, то граничні умови рівняння (6.401) приймають вид J = J1 при у = –S і J = J2 при у = S. Тоді розподіл температури підпорядковується наступному закону:
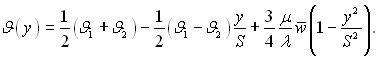 (6.402)
(6.402)
Тут останній член визначає зміну температури, викликану теплотою тертя, що накладається на явище власно теплопровідності.
Тепловий потік на стінці ![]() де п – нормаль до стінки, при цьому додатним вважається напрямок від стінки до рідини.
де п – нормаль до стінки, при цьому додатним вважається напрямок від стінки до рідини.
Для нижньої стінки J = J1 і
![]() (6.403)
(6.403)
для верхньої стінки J = J2, і
![]() (6.404)
(6.404)
Сумарний тепловий потік через обидві стінки
![]() (6.405)
(6.405)
Потік теплоти від гарячої стінки J2 до холодної J1, під впливом теплоти тертя, може бути спрямованим до гарячої стінки (q2 ≥ 0) так, що і вона буде сприймати теплоту. Цей ефект виникає за умови
![]() (6.406)
(6.406)
У випадку q2 = 0 приток тепла до нижньої стінки q1 подвоюється. Якщо температура обох стінок однакова: J1 = J2, то згідно рівнянню (6.402) настає розподіл температури за параболою четвертої степені; максимальна температура на осі каналу незалежно від його ширини визначається рівнянням
![]() (6.407)
(6.407)
Якщо нижня стінка теплоізольована, то граничні умови рівняння (6.401) запишуться в виді J = J2 при у = +S і dJ/dy = 0 при у = –S. При цьому розв’язок має вид
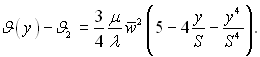 (6.408)
(6.408)
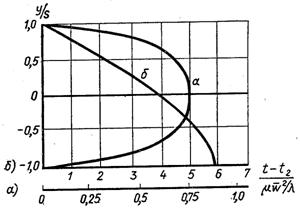
Рис.6.47. Розподіл температур у плоскій щілині з урахуванням теплоти тертя: а) теплопровідні стінки; б) нижня стінка теплоізольована
На рис.6.47 наведено розподіл температур за висотою щілини для розглядуваних умов тепловіддачі.
Температура тепло ізольованої стінки (адіабатна температура стінки) розраховується по формулі
![]() (6.409)
(6.409)
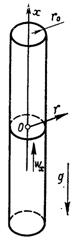
Рис.6.48. До задачі про теплообмін за сумісної дії вимушеної і вільної конвекції
Теплообмін в круглій трубі при сумісній дії вимушеної і природної конвекції. Розглянемо стабілізовану течію рідини в вертикальній круглій трубі при постійному тепловому навантаженні за довжиною труби (рис.6.48). Фізичні властивості рідини вважаємо сталими. Зміна її густини в залежності від температури підпорядкована лінійному закону і ураховується тільки в рівнянні руху при визначенні підйомної сили. Рух рідини в трубі здійснюється за рахунок вимушеної і природної конвекції. У системі координат, наведеній на рис.6.48 вихідна система рівнянь має наступний вид:
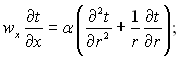 (6.410)
(6.410)
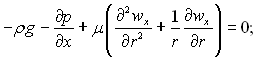 (6.411)
(6.411)
![]() (6.412)
(6.412)
![]() (6.413)
(6.413)
Для області теплової і гідродинамічної стабілізації маємо
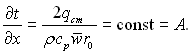 (6.414)
(6.414)
З урахуванням (6.413) і (6.414) перетворимо вихідні рівняння:
![]() (6.415)
(6.415)
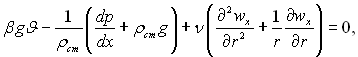 (6.416)
(6.416)
де ![]()
Задача зводиться до розв’язку цих рівнянь при граничних умовах:
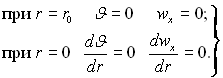 (6.417)
(6.417)
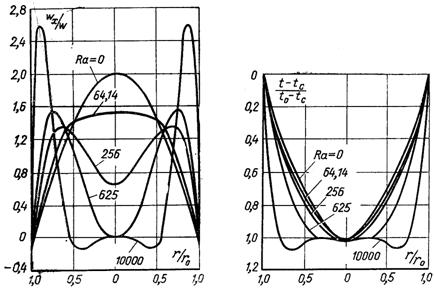
Рис.6.49. Розподіл швидкостей і температур за радіусом труби при різних
числах Релея (дt/дх > 0)
На рис.6.49 наведені розподіли швидкостей і температур при підйомній течії в трубі, що нагрівається. При значенні числа Релея (Ra = Gr·Pr) рівному нулю, профіль швидкості параболічний. Зі збільшенням числа Ra швидкість біля стінки збільшується, а в ядрі потоку – зменшується. При числі Ra = 630 швидкість на осі дорівнює нулю, а при подальшому збільшенні числа Ra виникає течія, спрямована в протилежний бік.
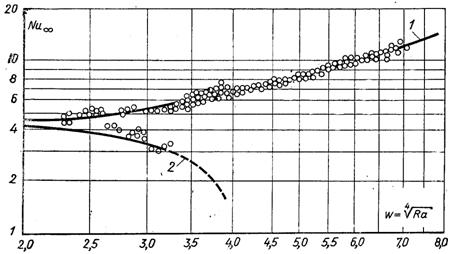
Рис.6.50. Залежність числа Nu від числа Ra при сумісній дії вимушеної і природної конвекції
[співставлення дослідних даних з розрахованими за (6.418]: 1– дt/дх > 0; 2 – дt/дх < 0
На рис.6.50 показана зміна числа Nu в залежності від числа Ra. При Ra→0 Nu→4,36. Як видно з рисунка результати теоретичного розрахунку добре погоджуються з дослідними даними. На підставі опрацювання дослідних даних запропоновано наступне розрахункове рівняння:
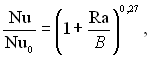 (6.418)
(6.418)
де Nu0 – число Нуссельта для випадку в’язкої течії рідини з постійними властивостями;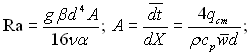
![]()
![]()
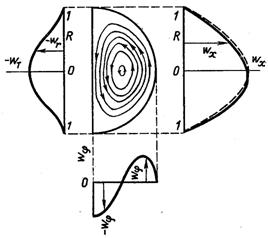
Рис.6.51. Лінії течії в перерізі горизонтальної труби при сумісній дії вимушеної і вільної конвекції
Усі фізичні параметри рідини вибираються за середньою температурою t( у даному перерізі труби. Рівняння (6.418) справедливий в області 250 < Ra <8·105; Re < Reкр; 3·104 < x < xпр; 4≤ Pr ≤ 6 при спів паданні вимушеної і вільної конвекції для qcm = const. Під час руху рідини в горизонтальній трубі внаслідок взаємодії вимушеної і вільної конвекції виникає складний, гвинтовий рух (рис.6.51). У цьому випадку порушується симетрія в розподілі швидкостей і температур. В наслідок цього число Нуссельта змінюється не тільки по довжині, а і по колу.
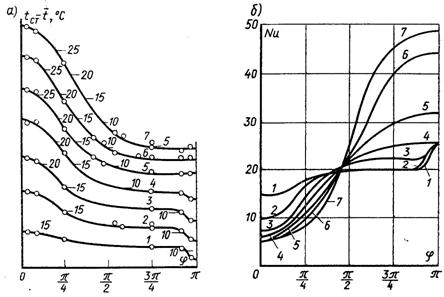
Рис.6.52. Розподіл температури (а) і місцевого числа Nu (б) по периметру труби при
значеннях![]() 1 –0,43; 2 – 0,75; 3 – 1,2; 4 – 2,3; 5 – 4,0; 6 – 6,0; 7 – 9,5
1 –0,43; 2 – 0,75; 3 – 1,2; 4 – 2,3; 5 – 4,0; 6 – 6,0; 7 – 9,5
На рис.6.52 наведені дані з розподілу температури стінки і числа Нуссельта для області стабілізованої течії (при Х > 1,7·10–3) і середніх значень чисел Нуссельта. На підставі дослідних даних запропоновано апроксимаційне рівняння
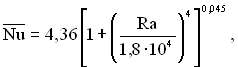 (6.419)
(6.419)
де ![]()