6.4. Методи розрахунку теплообміну в турбулентному пограничному шарі
Методи розрахунку теплообміну в турбулентному пограничному шарі, за своєю суттю, аналогічні розглянутим раніше методам розрахунку ламінарного пограничного шару з тією різницею, що при інтегруванні використовуються відповідні відносні закони теплообміну, які справедливі для турбулентного пограничного шару.
6.4.1. Розв’язок рівняння енергії турбулентного пограничного шару на непроникливій поверхні
Для випадку плоского пограничного шару при дозвукових швидкостях течії рідини інтегральне рівняння енергії записується в такому виді
(6.298)
Використовуючи закон теплообміну у вигляді (6.241) і після інтегрування його, отримаємо:
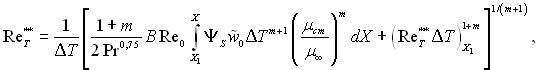(6.299)
де 
– число, яке розраховується за швидкістю набігаючого потоку при характерній довжині тіла L;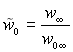 
– відносна швидкість на зовнішній границі пограничного шару; 
– лінійний розмір, який відраховується від передньої критичної точки, на якому існує ламінарний пограничний шар.
Значення добутку 
, що знаходиться в правій частині рівняння (6.299), знаходимо з розрахунку ламінарного пограничного шару. Локальне значення числа St визначаємо за рівнянням:
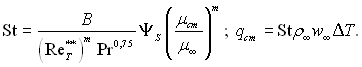(6.300)
У тому випадку, якщо необхідно знайти розподіл температури стінки при заданому законі підведення теплоти, методика розрахунку залишається тією ж, що і у випадку ламінарного пограничного шару. При цьому, з урахуванням закону теплообміну турбулентного пограничного шару при “стандартних” умовах (6.241) шуканий вираз для ΔТ набуває вигляду
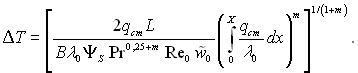(6.301)
При виводі цього рівняння вважалося, що турбулентний пограничний шар починається з передньої кромки (
= 0 при Х = 0).
При надзвуковому обтіканні поверхні теплообміну рівняння енергії (6.298) зберігає свій вигляд, якщо прийняти, що
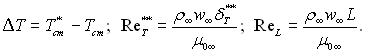
Число знаходимо з рівняння
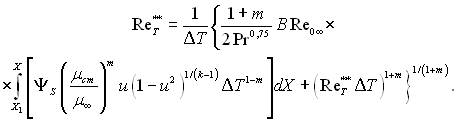(6.302)
У цьому рівнянні функція ΨS визначається за формулою (6.253).
При осьовій симетрії пограничного шару маємо
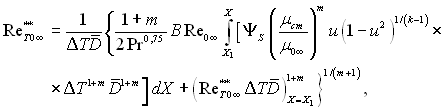(6.303)
де 
– безрозмірний діаметр поперечного перерізу тіла, що залежить від х.
У випадку течії газу в надзвуковому соплі з рівняння нерозривності потоку отримуємо:
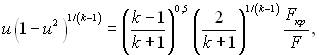(6.304)
де Fкр – площа критичного перерізу сопла; F – поточна площа прохідного перерізу сопла.
З урахуванням рівняння (6.304) із рівняння (6.303) отримуємо
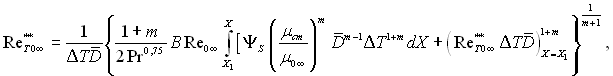(6.305)
де L = Dкр.
Локальні значення чисел Стентора і величина питомого теплового потоку визначаються за формулами:
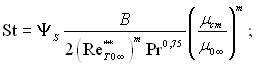(6.306)
(6.307)
При обтіканні пластини з постійною температурою стінки і при виникненні турбулентного пограничного шару на передній кромці пластини з рівнянь (6.298) і (6.241) отримуємо:
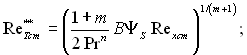(6.308)
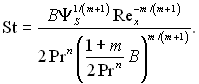(6.309)
При т =0,25 п = 0,75 і В = 0,0256 маємо
(6.310)
При обтіканні тупоносого тіла з постійною температурою стінки 
отримуємо:
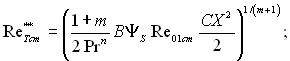(6.311)
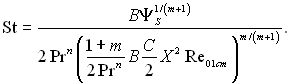(6.312)
де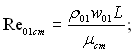 
w01 – швидкість набігаючого потоку.
В окремому випадку, для поперечного обтікання пластини С = 1 (якщо т = 0,25, В = 0,0256, п = 0,75), отримуємо:
(6.313)
У тих випадках, коли задається розподіл питомого теплового потоку на поверхні теплообміну, інтегральне співвідношення енергії приводиться до виду
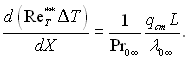(6.314)
Для граничних умов 
при Х = 0 для випадку qст = const маємо:
(6.315)
(6.316)
З цього слідує, що для любого заданого закону зміни швидкості на зовнішній границі пограничного шару вздовж обтічної поверхні при постійному тепловому навантаженні для розрахунку тепловіддачі справедлива формула для обтікання пластини, тільки в числах St і Re необхідно ставити параметри, які відносяться до зовнішньої границі пограничного шару для даного перерізу.
6.4.2. Розв’язок рівняння енергії турбулентного пограничного шару на проникливій поверхні
Рівняння енергії для розглядуваного випадку запишемо так
(6.317)
Функція ΨS для випадку дозвукової швидкості течії визначається за формулою
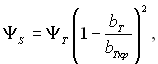(6.318)
де ΨТ визначається з виразу (6.271):
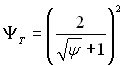
і bTкр – за рівняннями (6.281) і (6.283).
Інтеграл рівняння (6.317) в загальному випадку має такий вид:
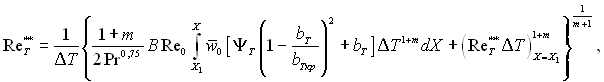(6.319)
При заданих функціях 
за рівнянням (6.319) визначаємо розподіл по х і величини .
Розподіл локального числа St знаходимо з виразу
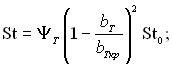(6.320)
розподіл витрат охолоджувального газу за довжиною контуру – з
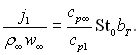(6.321)
Величину параметра проникливості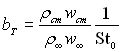 
, який входить в рівняння (6.318), (6.319) і (6.321), визначаємо з умови балансу теплоти на поверхні теплообміну. Методи визначення параметра проникливості для різних випадків теплообміну (пористого охолодження, конденсації, випаровування, вигорання теплозахисного покриття та ін.) розглянемо в § 6.7 і 8.1
Пористе охолодження знаходить широке застосування в області надзвукових швидкостей течії газу. Граничні закони тертя і теплообміну в цій області можна апроксимувати формулою
(6.322)
де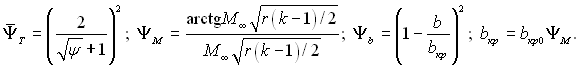 
Параметр bкр0 визначається за формулами (6.281) і (6.283). Величину питомих теплових потоків у цьому випадку визначаємо за формулою
(6.323)
де 
Досліди показують помітне зменшення коефіцієнта поновлення r зі збільшенням інтенсивності вдування. Для урахування цього впливу можна використати наступне рівняння
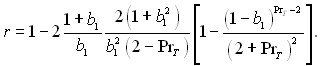(6.324)
6.5. Теплообмін при вимушеній течії рідини в трубах
Напірний (вимушений) рух в трубах є основним в різного роду технічних пристроях і технологічних процесах. У більшості теплових апаратів (котлах, пароперегрівачах, конденсаторах, теплообмінниках та ін.) рух одного з теплоносіїв здійснюється циліндричними каналами. Тому знання основних закономірностей теплообміну при подібній течії теплоносія необхідне для розрахунку і проектування різних теплообмінних апаратів
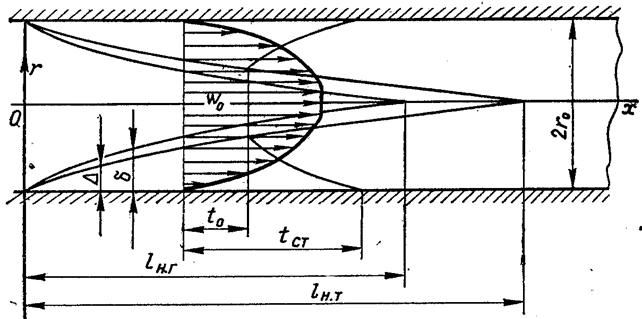
Рис.6.37.Розвиток динамічного і теплового пограничних шарів на початковій ділянці труби
Якщо розподіли швидкості і температури рідини на вході в трубу рівномірні, то вздовж стінки труби починають розвиватися динамічний δ і тепловий Δ пограничні шари (рис.6.37). Товщина пограничного шару по довжині труби збільшується і, вкінці, заповнює весь живий переріз.
В залежності від умов течії і входу рідини в трубу пограничний шар може бути ламінарним, турбулентним чи складатися із зон ламінарного, перехідного і турбулентного режимів руху.
Після проходження рідиною перерізу, в якому пограничні шари змикаються, в трубі установлюється постійний розподіл швидкостей – у формі параболи для ламінарного режиму течії і форму випуклої кривої для турбулентного (рис.6.38). Відстань від входу до цього перерізу називається довжиною початкової ділянки чи ділянкою гідродинамічної стабілізації ℓп.г.
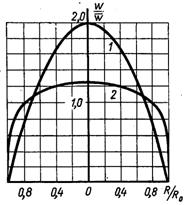
Рис.6.38. Профілі швидкостей в трубі: 1 – ламінарний; 2 – турбулентний режими руху
При наявності теплообміну під час руху рідини вздовж труби спостерігається прогрів чи охолодження пристінного шару. При цьому на початку труби центральне ядро рідини зберігає температуру, яка дорівнює температурі на вході, і в теплообміні не приймає участь. Зміна температури відбувається в пристінному шарі товщиною Δ. Таким чином, біля поверхні труби на її початковій ділянці утворюється тепловий пограничний шар, товщина якого при віддаленні від входу збільшується. На певній відстані від входу, яка називається початковою тепловою ділянкою ℓп.т, теплові пограничні шари з’єднуються між собою, і в подальшому вся рідина приймає участь в теплообміні і безрозмірний профіль температур θ = (t – tcт)/(t0 – tст) для нестисливої рідини при tст = const залишається незмінним по довжині труби.
Коефіцієнт тепловіддачі на ділянці стабілізованої течії визначають за перепадом температур між середньобалансовою t(0 і температурою стінки, тобто
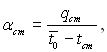де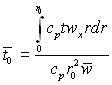 
.
Внаслідок того, що на ділянці термічної стабілізації градієнт температури зменшується скоріше, ніж температурний напір коефіцієнт тепловіддачі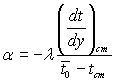 
зменшується, прямуючи до сталої величини, яка характерна для стабілізованої течії (рис.6.39).
Рух рідини в трубах може бути ламінарним і турбулентним. Про режим течії судять за величиною числа Рейнольдса Re = wd/ν.
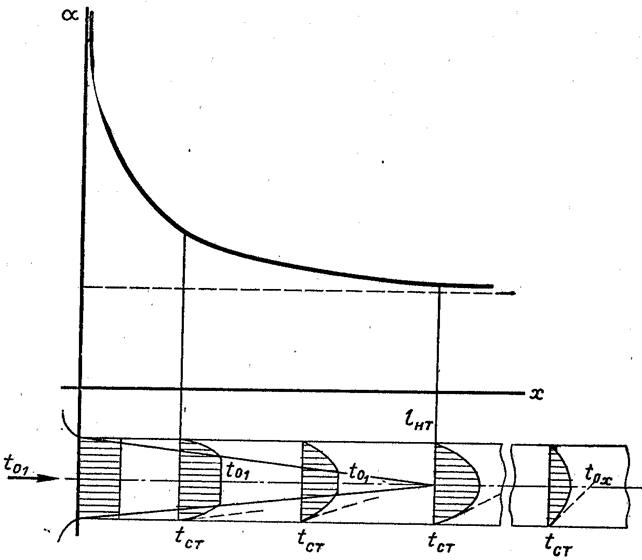
Рис.6.39. Зміна коефіцієнта тепловіддачі за довжиною труби
Якщо Re < Reкр1, то течія ламінарна. Дослідження показують, що при ізотермічній течії в круглих трубах Reкр1≈ 2300. Розвинений турбулентний рух в технічних трубах установлюється при Re > Reкр2 ≈ 10000. Рух у межах Reкр1 < Re < Reкр2 називається перехідним чи нестійким турбулентним рухом. При перехідному режимі турбулентність з’являється на певній довжині труби, далі рідина, що турбулентно рухається, виноситься потоком. Зміна ламінарного і турбулентного станів відбувається через нерівномірні проміжки часу і характеризується коефіцієнтом переміжності γ, що показує, яку частку деякого проміжку часу в певному місці труби займає турбулентна течія. Для ламінарної течії γ = 0, для турбулентної γ = 1 (рис.6.40).
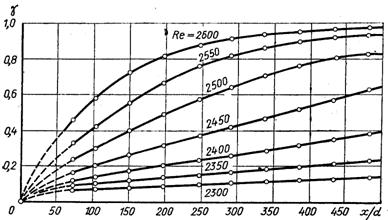
Рис.6.40. Залежність коефіцієнта переміжності γ в трубі від поточної довжини х при різних числах Рейнольдса
На величину Reкр суттєво впливає форма потоку, яка визначається формою труби. Так, у збіжних каналах (конфузорах) Reкр більше, ніж в трубах, а в розбіжних каналах (дифузорах) – менше. Для прямих квадратних і прямокутних труб дослідне значення Reкр визначається за еквівалентним діаметром, і це значення близьке до значень в круглих трубах. В трубах, перерізи яких мають вузькі кутові зони, можливе одночасне існування ламінарного і турбулентного режимів руху. У цьому випадку критичне число Рейнольдса, за якого течія залишається ламінарною за всім живим перерізом, оказується значно меншою 2300. Для гнутих круглих труб зі зменшенням радіуса гину труби значення Reкр збільшується. Під час руху рідини по зігнутій трубі на кожну частинку діють відцентрові сили, які залежать від швидкості руху рідини і радіуса гину труби. Внаслідок цього в зігнутій трубі виникає додаткова поперечна циркуляція рідини. Досліди показують, що в зігнутих трубах при невеликих D/d величина Reкр значно більша, ніж в прямих, що пояснюється стабілізуючим впливом відцентрових сил. Для області 3 ≤ R/d ≤ 200 для визначення Reкр можна рекомендувати експериментальну формулу
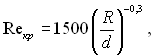
де R – радіус гину труби.
Шорсткість на поверхні стінки труби у загальному випадку сприяє переходу ламінарного руху в турбулентний, тому що викликає в ламінарному шарі додаткові подразнення. Інтенсивність цих подразнень залежить від нерівностей профілю. Як показують досліди, вплив шорсткості на Reкр починається зі значення ReS = w0k/ν = 120, де k – висота нерівностей профілю.
Рух рідини в умовах теплообміну може суттєво відрізнятися від ізотермічного за рахунок залежності фізичних властивостей від температури. У цьому випадку і критичні числа Рейнольдса відрізняються від значень, наведених для ізотермічних течій. В окремому випадку, під час руху рідини в вертикальних трубах в умовах суттєвої неізотермічності помітний вплив на розподіл швидкостей і стійкість ламінарної течії можуть чинити підйомні сили.
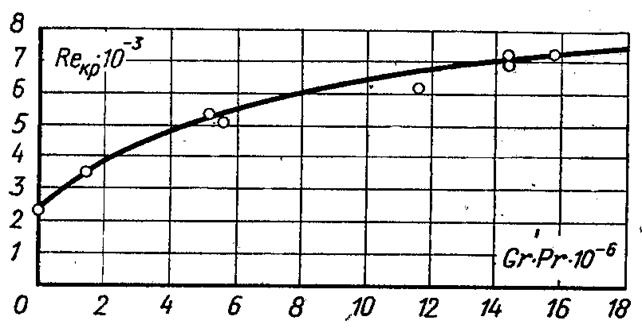
Рис.6.41.Критичне число Рейнольдса в залежності від числа Релея при спів паданні вільної і вимушеної конвекції
На рис.6.41 наводиться залежність критичного числа Рейнольдса від числа Gr·Pr у вертикальній трубі при співпадінні вимушеної і вільної конвекції. З графіка видно, що із збільшенням Gr·Pr значення критичного числа Рейнольдса збільшується, що пояснюється наповненням профілю швидкостей в пристінному шарі зі збільшенням Gr·Pr.
Великий вплив на значення Reкр чинить форма входу в трубу. При хорошому заокругленому вході і відсутності подразників можна збільшити Reкр до 4·104. Довжина вхідної ділянки, на якій початкові подразнення можуть затухати чи збільшуватися, складає, за різними даними, від 50 до 130 d труби.
При вивченні теплообміну в трубах в основному приймають два методи дослідження, які дозволяють отримати кількісні залежності
Перший метод стосується аналітичного розвязку системи диференціальних рівнянь при певних припущеннях і граничних умовах.
Другий метод дослідження передбачає застосування методів теорії подібності і розмірності, при цьому конкретні розрахункові залежності отримують за допомогою критеріального опрацювання дослідних даних.
