7.1.2. Горизонтальний циліндр

Для Ra < 7·10¹⁰ існує аналітичний розв’язок задачі про тепловіддачу довгого горизонтального циліндра в умовах природної конвекції. Це рішення ґрунтується на теорії ламінарного пограничного шару і добре погоджується з результатами вимірів.

Аналітичне рішення для циліндра, так само як і для випадку обтікання пластини, отримано шляхом заміни змінних, який дозволяє перетворити рівняння пограничного шару в звичайне диференціальне рівняння. Таке перетворення можливе тому, що рішення розглядуваної задачі відноситься до класу подібних розв’язків.

Теоретичне рішення, отримане Германом для довгого горизонтального циліндра, приводить до формули

(7.32)

де х – криволінійна координата, яка відраховується від передньої критичної точки вздовж контуру циліндра; d – діаметр циліндра; α_х – локальне значення коефіцієнта тепловіддачі; f(φ) – деяка функція, яка залежить від центрального кута φ (розраховується від передньої критичної точки). Значення функції f(φ), отримані розрахунковим шляхом, такі:

Формула (7.32) справедлива для ламінарного режиму течії в пограничному шарі при Pr = 0,73.

Вплив на теплообмін числа Прандтля можна визначити, користуючись наступною залежністю:

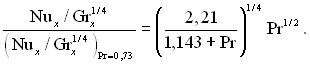
З формули (7.32) для локального значення числа Нуссельта (Nu_x) можна отримати формулу для середнього по поверхні циліндра числа Нуссельта:

(7.33)

де – коефіцієнт тепловіддачі осереднений по поверхні циліндра; d – діаметр циліндра.

При рівних числах Грасгофа і ℓ = d середній коефіцієнт тепловіддачі для вертикальної пластини в 1,29 рази більше, ніж для горизонтального циліндра.

Для розрахунку середньої тепловіддачі горизонтального циліндра при різних числах Прандтля можна використовувати результати отримані сполученням деяких теоретичних міркувань з емпіричними коефіцієнтами:

У всьому діапазоні чисел Ra ці дані добре погоджуються з дослідними результатами, отриманими в дослідах з повітрям, бутаном, хлористим етилом і маслом різними дослідниками. При числах Ra > 10⁵ і Pr = 0,74 ці дані з точністю до 2% співпадають з розрахунками за рівнянням (7.33), отриманими шляхом розв’язку рівнянь пограничного шару для горизонтального циліндра. Використовуючи наведені дані фізичні параметри середовища слід відносити до температури 0,5(Т_ст + Т_р).

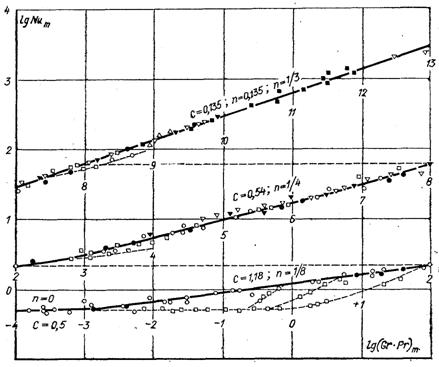
Рис.7.6.Тепловіддача під час вільного руху рідини для тіл різної форми

У літературних першоджерелах наводяться наближені залежності подібності, які з певною похибкою дозволяють узагальнити експериментальні дані з природної конвекції для тіл простої форми: вертикальних пластин, вертикальних і горизонтальних циліндрів і куль. Така формула (7.34), отримана шляхом опрацювання великої кількості дослідних даних різних авторів наведених на рис.7.6:

(7.34)

При отриманні цієї формули за характерний розмір для вертикальних пластин приймалася висота, а для горизонтальних циліндрів і куль – діаметр. Фізичні параметри віднесені до температури 0,5(Т_ст + Т_р), Pr > 0,7.

Аналіз експериментальних результатів показав, що в діапазоні 10^–32 при обтіканні цих тіл має місце режим, який можна назвати режимом псевдотеплопровідності. У названому діапазоні чисел Релея п = 1/8, а С = 1,18.

У режимі псевдотеплопровідності розподіл температур в середовищі, що оточує тіло, тільки незначно відрізняється від температурного поля в умовах чистої теплопровідності яке мало б місце при повній відсутності руху в середовищі.

Для діапазону 5·10² < Ra < 2·10⁷ характерне існування сформованого ламінарного пограничного шару біля поверхні тіла. Це режим розвиненої ламінарної конвекції, для якої п = 1/4, а С = 0,54.

Діапазон 2·10⁷ < Ra < 10¹³ включає перехідний турбулентний режим течії в пограничному шарі. У цьому діапазоні п = 1/3, а С = 0,135.

У дійсності перехід від одного режиму до іншого відбувається досить плавно. Кожний режим охоплює трохи більшу область зміни чисел Релея, ніж це указано. Границі цих режимів у значній мірі залежать від умов розвитку процесу і зовнішніх подразників, які мають місце під час проведення дослідів.

У формулі (7.34) визначальним є число Ra = Gr·Pr. Така залежність характерна для течій, в яких сили інерції, що діють в рідині чи газі, малі в порівнянні з силами внутрішнього тертя, викликаними в’язкістю.

Аналіз системи рівнянь руху, нерозривності потоку і енергії методами теорії подібності і розмірності показує, що при повній відсутності сил інерції в рідині інтенсивність теплопереносу за умов природної конвекції пропорційна безрозмірному комплексу Gr·Pr. Але при малих числах Прандтля, характерних для рідких металів, сили інерції стають співрозмірними з силами внутрішнього тертя і названа пропорційність порушується. За цих умов опрацювання дослідних даних в змінних Nu, Ra призводить до розшарування даних за числами Pr.

З теорії подібності відомо, що обов’язковим посиланням подібності фізичних явищ є геометрична подібність тіл. Узагальнення дослідних даних для тіл різної форми, отримане з певним розкиданням дослідних точок, оказується можливим завдяки тому, що на природну конвекцію у великому об’ємі вплив форми має другорядне значення.

Суттєво, що при розвиненій турбулентній течії у пограничному шарі інтенсивність переносу теплоти практично не залежить від розмірів тіла, оскільки показник степеня біля числа Релея недалекий від 1/3. Ця закономірність дозволяє вивчати процес на зменшених моделях.

Використовуючи для розрахунків тепловіддачі залежності, отримані методами теорії подібності, необхідно пам’ятати, що межі їх застосування визначаються діапазоном визначальних безрозмірних комплексів (Gr, Pr, Ra), в яких вони отримані. Крім цього, необхідно мати на увазі, що кожна залежність справедлива за умови, що характерний розмір тіла і визначальна температура для фізичних параметрів будуть прийняті точно такими ж, якими вони були вибрані при отриманні формули.

7.2. Теплообмін при вільному русі в обмеженому об’ємі

При розгляді випадків теплообміну при природній конвекції в необмеженому просторі спостерігається, що процеси нагрівання чи охолодження рідини відбуваються на значних відстанях, а висхідні і низхідні токи не впливають один на одного.

В обмеженому об’ємі товщина пограничного шару стає співрозмірною з розмірами самого простору і процеси нагрівання і охолодження неможна розглядати незалежно.

Якщо у великому об’ємі інтенсивність переносу теплоти порівнянно слабко залежить від форми обтічного тіла, то в обмеженому об’ємі процес формування швидкісного і температурного полів в рідині чи газі здійснюється під сильним впливом форми стінок.

Процеси теплообміну при природній конвекції в обмеженому просторі зустрічаються в багатьох технічних пристроях. З цими процесами зв’язана теплова ізоляція трубопроводів, будівель, печей, і ємностей за допомогою газових прошарків; формування температурних полів і перенос теплоти у відсіках і баках надзвукових літаків, ракет і космічних літальних апаратів; теплообмін у радіоелектронних пристроях; перенос теплоти в пористих тілах і середовищах. Процеси теплообміну при природній конвекції мають практичне значення, коли приходиться мати справу з нагрітими рідинами, які залишаються в замкненому просторі, а також у криогенній техніці при тривалому зберіганні стислих газів.

Особливий інтерес для практичних додатків представляє собою випадок переносу теплоти через горизонтальну, вертикальну чи похилу плоску щілину, а також перенос теплоти через кільцевий чи кулястий прошарок, заповнений рідиною чи газом.

7.2.1. Довгі горизонтальні шари

У випадку, коли горизонтальний шар рідини чи газу гріється зверху, у полі течії настає стан гідростатичної рівноваги і перенос теплоти крізь шар може здійснюватися тільки шляхом теплопровідності і теплового випромінювання. Відсутність конвекції можлива тільки в строго горизонтальному шарі при T₁ > T₂ і однорідному розподілі температур на границях шару. За цих умов холодні частинки з більшою густиною знаходяться біля нижньої стінки з температурою Т₂ і не можуть спускатися нижче, а нагріті частинки, з меншою густиною, знаходяться біля верхньої нагрітої стінки з температурою Т₁ і не можуть підійматися вище. Це випадок стійкого розшарування густини.

При нагріванні шару газу знизу (Т₂ > Т₁) при певних умовах також можлива гідростатична рівновага в газі. Вважаючи в рівняннях руху і енергії складові вектора швидкості рівними нулю і вважаючи газ нев’язким і нетеплопровідним, отримаємо систему рівнянь, які відтворюють умови гідростатичної рівноваги у стисливому ідеальному газі, для якого р = ρRT:

(7.35)

У цьому рівнянні вважається, що ось х спрямована вертикально вгору, а напрямок вектора прискорення вільного падіння g у протилежно додатному напрямку осі х.

З цих рівнянь виходить, що за умови гідростатичної рівноваги

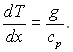(7.36)

Виникнення конвекції можливе тільки у випадку, коли

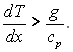(7.37)

З фізичної точки зору це значить, що збільшення густини у від’ємному напрямку осі х під дією сили тяжіння компенсує зменшення густини за рахунок нагріву нижньої стінки і при виконанні умови (7.37) гідростатична рівновага газу не порушується.

На підставі більш строгої теорії, яка враховує вплив в’язкості і теплопровідності в нестисливій рідині, показано, що у безмежно довгому горизонтальному шарі рідини, який гріється знизу, конвекція виникає при

Ra = Gr·Pr > Ra_кр, (7.38)

де 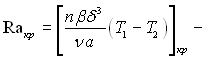деяке критичне значення числа Релея, Ra_кр = 1700; δ – товщина шару (відстань між нагрітими стінками).

Таким чином, неоднорідний розподіл густини в рідині чи газі не завжди приводить до виникнення вільного руху. Конвекція виникає тільки за умови нестійкого розшарування густини.

Теоретичні дослідження привели до виявлення умови (7.38), що підтверджено дослідним шляхом. Показано, що після виникнення термічної нестійкості в горизонтальній щілині, заповненій рідиною, виникає рух з комірчастою структурою потоку, що підтверджується візуальними спостереженнями за допомогою прозорих стінок і зважених в рідині твердих частинок.

Використовуючи аналогію з вібраційною діафрагмою, Релей теоретично показав, що така шестикутна (у плані), комірка відповідає найбільш стійкій формі течії.

При 1700 < Ra < 3000 внаслідок малої швидкості течію можна називати повзучою. У цьому діапазоні чисел Релея

Nu = 0,0012Ra^0,9. (7.39)

При виникненні конвекції рідина підіймається в центрі шестикутної комірки і опускається на її периферії. В дослідах з повітрям спостерігається протилежна за напрямком картина течії. Ці особливості течії зв’язані з різним характером залежності в’язкості від температури для рідин і газів. В’язкість газів збільшується з підвищенням температури, у той час як у рідин ця залежність протилежна. Напрямок розповсюдження початкових подразнень при виникненні конвекції, в свою чергу, залежить від того, як змінюється в’язкість всередині шару.

Режим розвиненої ламінарної конвекції наступає при більш високих значеннях чисел Релея. Для 3000 < Ra < 25000 характерним стає степеневий закон зміни числа Нуссельта в залежності від числа Релея:

Nu = 0,24Ra^1/4. (7.40)

У цьому діапазоні чисел Релея при дотриманні ізотермічності границь може існувати двомірна структура течії у вигляді довгих валів, які чергуються, і осі симетрії яких паралельні стінкам щілини. При цьому в міру збільшення числа Релея відношення чергування висхідних і низхідних токів в товщині шару збільшується від 2 до 2,8.

При більш високих числах Ra течія стає трьохмірною з признаками переходу до турбулентного режиму. У діапазоні 25000 < Ra < 30000 справедлива наступна формула:

Nu = 0,3Gr^0,16Pr^0,21. (7.41)

При Ra > 30000

Nu = 0,1Gr^0,31Pr^0,36. (7.42)

Оптичні виміри показують, що турбулентний режим руху в довгому горизонтальному шарі рідини з’являється при Ra > 50000. Більш пізні дослідження показали, що крім числа Релея перехід до турбулентного режиму залежить також і від числа Прандтля. В недуже в’язких середовищах турбулентність з’являється при більш низьких числах Релея.

Із рівнянь (7.41) і (7.42) виходить, що при Ra > 25000 число Релея не є єдиним визначальним безрозмірним комплексом. При більших числах Релея вплив на теплообмін числа Грасгофа і Прандтля стають неоднаковими. У формулах (7.39)...(7.42) числа подібності побудовані наступним чином:

(7.43)

Усі величини, які визначають фізичні властивості середовища, віднесені тут до середньої температури в підшарі 0,5(Т₁ + Т₂). За характерний розмір прийнято товщину підшару δ. В інженерних розрахунках теплопереносу через підшари і щілини вводиться поняття еквівалентного коефіцієнта теплопровідності λ_е.

Середнє значення числа Нуссельта для плоского підшару отримано тут у вигляді відношення λ_е до теплопровідності середовища λ, яке заповнює підшар. Таким чином, середнє число Нуссельта показує, у скільки разів збільшується інтенсивність переносу теплоти за рахунок природної конвекції у порівнянні з інтенсивністю перенесення теплоти в умовах чистої теплопровідності.

За середнім значенням числа Нуссельта визначається середня густина теплового потоку, який проходить крізь шар рідини чи газу:

(7.44)

Необхідно мати на увазі, що за розглядуваних умов завдяки складної вихрової структури течії в підшарі, локальні (місцеві) числа Нуссельта змінюються вздовж границь підшару. Значення локальних чисел Нуссельта Nu₁ і Nu₂ для підшарів визначаються наступними співвідношеннями:

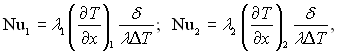(7.45)

в яких індекси “1” і “2” означають, що даний параметр відноситься до температури стінки Т₁ чи Т₂ відповідно, ΔТ = Т₂ – Т₁ (Т₂ > Т₁ ); λ – теплопровідність середовища при середній температурі в шарі; λ₁ і λ₂ – теплопровідності середовища при температурі Т₁ і Т₂ відповідно. При постійних фізичних властивостях середовища λ₁ = λ₂ = λ. У межах кожної вихрової комірки локальне число Нуссельта зменшується в міру того, як товщина температурного пограничного шару збільшується.

Наведені формули справедливі для довгих горизонтальних шарів, які гріються знизу. Для шарів обмеженої довжини наявність бокових стінок приводить до збільшення критичного числа Релея, яке визначає умови виникнення конвекції.

Завдяки впливу бокових стінок інтенсивність теплопереносу через шар зменшується. Це особливо помітно при низьких числах Релея біля порогу стійкості.

7.2.2. Вертикальні шари

У вертикальному шарі газу чи рідини, обмеженому плоскими твердими стінками з різними температурами, під дією різниці температур виникає нестійке розшарування густини і гідростатична рівновага існувати не може. Конвективний рух виникає відразу, як тільки число Релея стає відмінним від нуля, і плавно збільшується зі збільшенням числа Релея.

У вертикальних шарах виникає циркуляційна течія з висхідним потоком вздовж вертикальної стінки, яка має більш високу температуру, і низхідним потоком біля стінки з низькою температурою.

Розглянемо конвекцію у вертикальних прямокутних порожнинах, горизонтальні границі яких теплоізольовані.

За існуючими даними, можна назвати наступні орієнтовні границі для режимів течії і теплообміну. За природної конвекції повітря у вертикальному шарі з відношенням висоти до товщини, рівним 10, в діапазоні 0 < Gr < 2800 – режим псевдотеплопровідності, за якого інтенсивність теплопереносу залишається на рівні чистої теплопровідності, не дивлячись на те що швидкості в полі течії відмінні від нуля. (Тут число Gr побудовано по ширині щілини δ). При 2800 < Gr < 25000 існує певний проміжний режим, який передує виникненню температурних пограничних шарів на вертикальних стінках, які підтримуються при постійних, але різних температурах. в діапазоні 25000 < Gr < 320000 виникає режим розвиненої ламінарної конвекції. Цей режим можна також назвати режимом пограничного шару. В області 320000 < Gr < 1000000 всередині шару спостерігається виникнення вторинних течій у вигляді окремих крупних вихорів, які накладаються на основну циркуляційну течію. Приблизно при 10⁶ < Gr < 10⁷ починаються явища, які передують переходу до турбулентного режиму: утворення дрібних вихорів і виникнення нестаціонарних пульсацій. Розвинена турбулентна течія спостерігається при Gr > 10⁷. Границі цих режимів залежать від числа Pr і відношення сторін області.

Для розрахунку інтенсивності теплопереносу через довгі вертикальні шари повітря можна використовувати наступне рівняння:

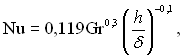(7.46)

де h – висота прямокутної порожнини; δ – відстань між нагрітими стінками.

Ця формула справедлива при 10³ < Gr < 5·10⁶ і 2,3 < h/δ < 47.

Для крапельних рідин існує емпірична формула

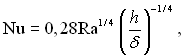(7.47)

яку можна використовувати при 10³ < Ra < 10⁷ і 5 < h/δ < 20. Досліди, за результатами яких отримана ця формула, виконувалися з водою, етанолом, маслом, гліцерином, а також з деякими іншими рідинами і охоплюють широкий діапазон чисел Прандтля.

У формулах (7.46) і (7.47) фізичні властивості теплоносія відносяться до середньої температури шару. При отриманні чисел Gr і Ra за характерний розмір прийнята відстань між нагрітими стінками δ; ΔТ = Т₂ – Т₁, де Т₁ і Т₂ – температури вертикальних меж області (Т₂ > Т₁). Середнє число Нуссельта, яке визначає інтенсивність теплопереносу через шар, побудовано так само, як і у випадку горизонтальних шарів.

У режимі розвиненої ламінарної конвекції локальні числа Нуссельта суттєво змінюються вздовж вертикальних стінок. На більшій частині нагрітої стінки локальне число Нуссельта зменшується у напрямку руху висхідного потоку. На холодній стінці локальне значення числа Нуссельта зменшується в напрямку руху низхідного потоку. Певні відхилення від цієї закономірності спостерігаються тільки на початкових ділянках вертикальних стінок, тобто у тому місці, де відбувається формування пограничного шару.

Виходить, що найбільш інтенсивний теплоперенос має місце в порожнині з відношенням висоти h до ширини δ; Δ рівним приблизно 1,5. Ці дані отримано при 10⁴ < Ra < 5·10⁴. Залежність числа Nu від h/δ; δ наведено на рис.7.7.

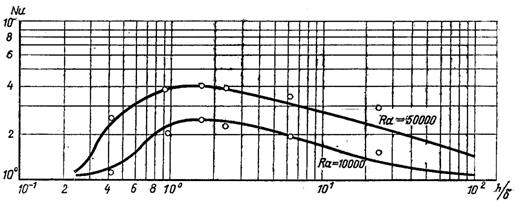
Рис.7.7. Залежність тепловіддачі від відношення сторін прямокутної порожнини. Суцільними лініями позначені теоретичні розрахунки, точки відповідають дослідним даним

Для турбулентного режиму течії у вертикальному шарі існує наступне рівняння подібності:

(7.48)

Це рівняння отримано для змішаних граничних умов, тобто для випадку, коли на одній із вертикальних стінок підтримується постійна густина теплового потоку q_ст = const, а на іншій задана температура Т_ст = const. Це рівняння справедливе для 10⁶ < Ra < 10⁹, 1 < Pr < 20 і 1 < h/d < 40. Число Релея тут містить у собі різницю температур на вертикальних границях. (На границі з q_ст = const температура змінюється за висотою стінки). За характерний лінійний розмір прийняти ширина шару δ. Фізичні властивості середовища віднесені до заданої температури Т_ст = const.