ЧАСТИНА ТРЕТЯ ТЕПЛООБМІН ПРИ ЗМІНІ АГРЕГАТНОГО СТАНУ. КОНДЕНСАЦІЯ
Розділ 8. ПОВЕРХНЕВІ ЯВИЩА І ФАЗОВА РІВНОВАГА
8.1. Капілярні ефекти першого і другого роду
Процеси конденсації пари характеризуються співіснуванням фаз і, як наслідок, наявністю поверхні розділу. Для утворення границі розділу фаз необхідно затратити певну роботу А. При постійних об’ємі, тиску і температурі робота утворення границі розділу, віднесена до одиниці поверхні, характеризується величиною поверхневого натягу σ, Дж/м2:
(8.1)
Рівняння (8.1) є визначенням поверхневого натягу. Значення поверхневого натягу згідно (8.1) додатне, тому що dA/dF < 0. Затрата роботи приводить до збільшення внутрішньої енергії міжфазного шару на величину dUF = σdF. Надлишкова внутрішня енергія міжфазного шару тут обумовлена тільки поверхневим натягом.
Рис.8.1. Поверхня розриву фаз
Особливі властивості міжфазного шару (поверхні розриву) викликані співіснуванням двох різних за своїми властивостями фаз 1 і 2 (рис.8.1). Границі міжфазної області зв’язані з далеко дією міжмолекулярних сил. Сили міжмолекулярної взаємодії швидко зменшуються з відстанню, тому можна говорити про певну ефективну товщину поверхні розриву І, за межами якої вплив суміжної фази стає несуттєвим.
У наближенні Гіббса міжфазну область розглядають такою, що не має товщини, але має певні реальні властивості, характерними фазі (поверхня розділу ІІ). Зауважимо також, що в механіці суцільних середовищ, положення які будуть широко використовуватися в наступних розділах, товщиною поверхні розділу нехтується.
Згідно термодинамічної теорії капілярності в системі з двох однорідних фаз 1 і 2, які дотикаються у вузькій перехідній області, яка може бути плоскою чи викривленою, довільна екстенсивна термодинамічна властивість всієї системи можна розглядати як суму трьох внесків: внеску фази 1, внеску фази 2 і внеску міжфазної області (поверхні розриву) 12 – рис.8.1.
У цьому разі внутрішня енергія всієї системи є сумою окремих складових:
U = U1 + U2 + U12. (8.2)
У цьому рівнянні індексами 1, 2 і 12 позначаються відповідно внутрішня енергія об’ємних (масових) фаз 1 і 2 і міжфазного шару 12.
Величина U12 це певна надлишкова енергія, яка обумовлена наявністю в системі міжфазної області. В подальшому надлишкові величини будемо позначати тильдою над символом.
Основне рівняння Гіббса, записане для надлишкової внутрішньої енергії буде мати наступний вигляд:
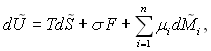(8.3)
де Т – температура; 
– надлишкова ентропія;
μі – хімічний потенціал і-го компоненту; 
– надлишкова маса і-го компоненту; F – поверхня натягу.
Рівняння (8.2) можна застосовувати і для скривлених поверхонь. Рівняння аналогічні (8.2), можна записати і для інших екстенсивних властивостей:
і так далі. Названі рівняння, як і рівняння (8.2), за своєю суттю є визначеннями надлишкових величин 
, , та інших. Ці рівняння необхідно вибирати так, щоб вони задовольняли рівнянням виду (8.2). Строго кажучи, значення надлишкових величин для викривлених шарів залежать від вибору положення умовної поверхні розділу, яка не має товщини. Вважається, що на поверхні розділу властивості змінюються стрибками.
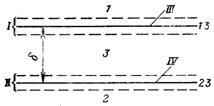
Рис.8.2. Будова товстої плівки: І, ІІ – поверхні розриву 13 і 23; ІІІ, ІV – поверхні розділу 13 і 23; δ – товщина плівки при кінцевій величині перехідних шарів
Розглянемо досить товсту плівку (рис.8.2) фази 3, яка знаходиться між об’ємними фазами 1 і 2 (наприклад, шар конденсату, що знаходиться на твердій поверхні і дотикається пари). Товсту плівку можна уявити собі як систему, що складається з фази 3 і поверхні розриву 13 і 23. Фаза 3 у напрямку нормалі до поверхні розриву 13 і 23, має набагато меншу протяжність, ніж в двох інших напрямках.
Основне рівняння теорії капілярності Гіббса (8.3) можна застосовувати і до плівок (як до проміжної поверхні):
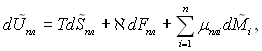(8.4)
де 
– надлишкова внутрішня енергія плівки; Т – температура; 
– надлишкова ентальпія; 
– хімічний потенціал і-го компоненту; 
– натяг плівки; Fпл – поверхня розриву фаз 1 і 2 (плівки).
Внаслідок цього термодинамічні закони, отримані для поверхневих шарів, можна використовувати і при дослідженні плівок. Плівку можна розглядати як таку, що має кінцеву товщину δ. Тоді замість (8.4) можна використовувати рівняння, у якому фігурують не надлишкові, а реальні величини, і яке аналогічне рівнянню для поверхні шарів кінцевої товщини:
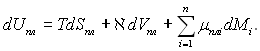(8.5)
Додаючи рівняння, записані аналогічним чином відповідно для фази 3 і поверхонь розриву 13 і 23, отримаємо:
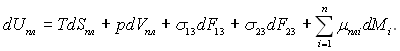(8.6)
З порівняння рівнянь (8.5) і (8.6) виходить, що натяг товстої плівки визначається виразом
(8.7)
Якщо плівки плоскі, то
(8.8)
У випадку тонких плівок шари 13 і 23 перекриваються і у плівці відсутня область, яка володіє властивостями фази 3. Остання може межувати з плівкою на її краях. Наведені умови можуть бути визначальними поняттями тонких плівок. Для тонких плівок умова адитивності надлишкової енергії областей 13 і 23 порушується – енергія стає функцією товщини плівки. Якщо поверхню розриву розглядувати згідно Гіббсу, то можна ввести поправку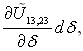 
яка враховує залежність надлишкової енергії від товщини плівки. У цій поправці 
– сумісна надлишкова енергія поверхонь розриву 13 і 23, обумовлена молекулярною взаємодією цих поверхонь.
Для термодинамічної рівноважної системи, яка характеризується рівністю температур, хімічних потенціалів і тисків, можна записати, що
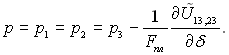(8.9)
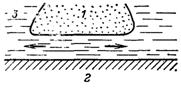
Рис.8.3. Течія у тонкій плівці
Індекси 1, 2 і 3 біля р позначають тиск у відповідних об’ємних фазах 1, 2 і 3, плівка вважається плоскою (рис.7.3).
З рівняння (8.9) виходить, що
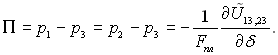(8.10)
Величина П відповідає тиску розклинення вперше виявленому і вивченому Б.В.Дерягіним і В.Є.Обуховим (1934 р.). Згідно їх даних тиск розклинення представляє собою надлишковий тиск тонкого шару рідини чи газу, який чинить перешкоду подальшому зростанню товщини плівки. Чи в іншій інтерпретації, тиск розклинення тонкого плоско-паралельного шару рідини, який розділяє два твердих тіла, дорівнює тиску, з яким (у додаток до нормального гідростатичного тиску в шарі) діє в стані рівноваги шар рідини на обмежуючі його тіла, намагаючись їх розсунути.
Тиск розклинення вважається додатним при відштовхуванні поверхневих шарів і від’ємним – при притягувані. Випадку незмочування плівкою поверхні тіла відповідає стан плівки, за якого вона намагається стати тоншою (тиск розклинення від’ємний). Під дією цього стискуючого тиску в плівці може розпочатися перетікання рідини у напрямку від малої товщини до більшої (див. рис.8.3). Протилежний напрямок руху повинен мати місце при змочуванні тіла рідиною.
При переході від товстих плівок до тонких рівняння (8.4) і (8.5) залишаються справедливими, якщо
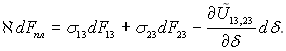(8.11)
Таким чином, натяг плівки, як суцільної субстанції, залежить від натягу поверхневих шарів і взаємодії між ними. Знак тиску розклинення завжди протилежний знаку похідної 
У разі недотримання рівності П = р1 – р3 = 0 тонкий шар потовщується чи стає тоншим в залежності від знака рівності П – (р1 – р3 ).
Поверхневий натяг σ залежить від природи двох співіснуючих фаз, їх складу, температури і тиску. Під час вивчення процесу теплообміну особливий інтерес викликає залежність поверхневого натягу від температури. Вигляд залежності пов’язаний з умовами, в яких знаходиться двофазна система. У загальному випадку зміна температури може привести до зміни тиску. Змінюється і склад фаз і поверхневого шару, якщо система не є однокомпонентною. З термодинаміки поверхневих явищ слідує, що зміна температури в багатокомпонентних системах при сталому тиску завжди супроводжується зміною складу. Зміна складу є додатковим фактором, який викликає зміну поверхневого натягу.
Вплив температури в однокомпонентній двофазній системі можна характеризувати наступною залежністю:
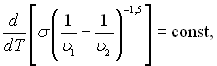(8.12)
де υ1 і υ2 молярні об’єми відповідно рідини і її пари.
З рівнянь, які дають залежність поверхневого натягу від температури, широко відоме рівняння Ван-дер-Ваальса:
(8.13)
У цьому рівнянні с – константа; п – додатна величина, п < 1; Ткр – температура, яка відповідає термодинамічній критичній точці. Згідно дослідних даних п ≈ 0,21. Для значень біля критичної точки Ван-дер-Ваальс отримав п ≈ 0,5. Рівняння Ван-дер-Ваальса показує на зменшення поверхневого натягу зі збільшенням температури.
Для бінарних сумішів залежність поверхневого натягу від складу якісно визначається нерівностями:
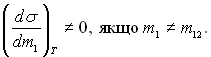(8.14)
Тут індексом 1 позначається фаза з більшою густиною (рідина), яка знаходиться в контакті з парою; індекс 12 – стосується поверхневого шару; т – концентрація і-го компоненту.
Нерівність (8.14) можна сформулювати у вигляді такого правила: якщо поверхневий шар рідкого розчину, який знаходиться у рівновазі з парою, збагачений одним з компонентів у порівнянні з рідкою фазою, то добавлення цього компоненту до розчину буде викликати зменшення поверхневого натягу; якщо ж поверхневий шар збіднений одним з компонентів у порівнянні з рідкою фазою, то добавлення цього компоненту до розчину буде викликати збільшення поверхневого натягу.
Зроблені висновки мають якісний характер. Для різних розчинів не існує строгої кількісної теорії, яка б дозволила розраховувати зміну поверхневого натягу в залежності від наявності домішки і виявила б кількісний зв’язок з іншими фізичними параметрами. Відсутній також метод, який дозволяє просто і надійно розрахувати склад поверхневого шару у багатокомпонентних системах для умов, коли компонент розподіляється між двома фазами.
Немає достатньої інформації про тиск розклинення. Тиск розклинення визначається тільки наближено і для самих простих випадків. Наближеність аналітичних рішень витікає із складності задачі. Неповнота дослідно-отриманих даних викликана не тільки технічними труднощами, але і з недосконалості аналітичного апарату, який використовується при опрацюванні дослідних даних.
Труднощі збільшуються внаслідок залежності тиску розклинення від великої кількості факторів: природи взаємодії фаз, товщини плівки, температури, складу фаз та ін.
Кількісну оцінку тиску розклинення в шарі рідини, товщина якого більша в порівнянні з міжмолекулярними відстанями, можна отримати, вважаючи що взаємодія тіл здійснюється завдяки флуктуаційного електромагнітного поля, існуючого завдяки термодинамічним флуктуаціям. Вважалося також, що плівка однорідна. Для розрахунку сили взаємодії достатньо знати комплексні діелектричні проникливості взаємодіючих середовищ як функції частоти монохроматичних складових флуктуаційного поля. Для випадку, коли товщина плівки δ << ch/kT, де с, h, k – відповідно швидкість світла і сталі Планка і Больцмана, і товщина плівки мала в порівнянні з довжинами хвиль, характерними для спектра поглинання взаємодіючих тіл, отримано, що за абсолютною величиною
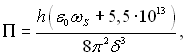(8.15)
де ε0 – електростатичне значення діелектричної проникливості; ωS – частота, яка відповідає максимальному значенню ε″ у дебаєвській області (ε=ε′+іε″). Величина ε0ωS є функцією температури.
Якщо δ << ch/kT і товщини плівки великі в порівнянні з довжиною хвилі, характерними для спектру поглинання взаємодіючих тіл, то
(8.16)
де П, як і раніше, виражається в Па.
Для достатньо товстих плівок, які характеризуються нерівністю δ>> ch/kT, можна написати:
(8.17)
При Т = 373 К величина ch/kT = 6·10–6 м. Таким чином, формулу (8.17) можна застосовувати, якщо δ ‰ 6·10–5 м.
Дослідження тиску розклинення для систем, які складаються з плівки рідини, твердої підкладки і проміжного шару речовини, що відрізняється за властивостями від рідини і підкладки. Для цих умов отримано наступне рівняння:
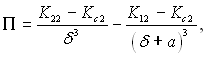(8.18)
де δ – товщина плівки; а – товщина сольватного шару; індекси 1, 2, “с” відносяться відповідно до твердої підкладки, плівки і сольватного шару. Коефіцієнти Кij характеризують силову взаємодію складових системи 1, 2, “с” і розраховуються за формулою:
(8.19)
де пV – концентрація молекул; bij – стала у формулі для енергії взаємодії двох молекул. Формулою (8.19) не враховується енергія відштовхування молекул, і потенціал притягання вважається зменшуваним зворотно пропорційно шостій степені відстані між молекулами.
Величина К22 – Кс2 служить мірою незмочування. Знак різниці К22 – Кс2 визначається співвідношенням сил взаємодії між молекулами конденсату і, з іншого боку, між молекулами конденсату і молекулами (чи групою атомів) сольватного шару (шару ліофобізатора).
Для води К22 значно перевищує Кс2, що обумовлено сильною дипольною взаємодією між молекулами води і відсутністю такої взаємодії між молекулами води і неполярними вуглеводневими радикалами молекул гідрофобізатора.
Якщо структура молекул гідрофобізатора така, що на поверхні знаходяться полярні групи, наприклад СООН, то характеристика незмочування різко погіршується внаслідок підсилення взаємодії молекул води і гідрофобізатора. Звідси випливають труднощі отримання крапельної конденсації органічних, а особливо неполярних, рідин. У цьому випадку сили взаємодії молекул рідини і ліофобізатора дуже близькі за величиною, внаслідок чого умова (К22 – Кс2) > 0 може не виконуватися.
Згідно формул (8.15)...(8.17) при δ→0 має місце П→∞. Цей вивід не відповідає інструментальним дослідженням. Вважаємо, що справедливість співвідношень виду П~δ–п виконується для розмірів δ >δ0, де δ0 – товщина стійкого адсорбційного шару конденсованої речовини. В області дуже малої товщини плівки величина П різко зменшується і змінює свій знак, що відповідає утворенню стійкої плівки.
Тиск розклинення може залежати від концентрації домішок, які містяться в розглядуваній системі. Так, для трифазної рівноваги пара – рідина – тверде тіло у випадку бінарної системи (і = 1, 2) і плоскої плівки маємо:
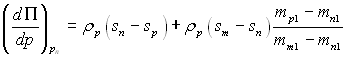(8.20)
і
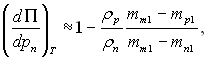(8.21)
де s – питома ентропія; т – концентрація і-го компоненту.
З рівняння (8.21) виходить, наприклад, що характер впливу тиску пари на тиск розклинення плівки, яка утворюється на твердому (чи рідкому) розчині, залежить від розподілу найбільш леткого компоненту між фазами: збільшення тиску пари приводить до збільшення тиску розклинення, якщо вміст найбільш леткого компоненту більший, ніж у твердому розчині.
У зв'язку з тим, що тонка плівка знаходиться в молекулярному силовому полі суміжних фаз, то можуть змінюватися її фізичні властивості, такі як в’язкість, теплопровідність та ін.
Таким чином, тиск розклинення залежить від природи тіл, які утворюють систему з участю плівки, її температури, товщини, тиску, концентрації в системі різних компонентів. У різних умовах тиск розклинення, як наслідок, буде залежати від швидкості зміни температури, інтенсивності дифузії і розчинності окремих компонентів, які присутні в розглядуваній системі, від можливих структурних змін фаз, порушення шару ліофобізатора та ін.
Такі параметри, як температура, тиск, концентрація і товщина плівки, при постановці крайових задач в рамках механіки суцільних середовищ є залежними змінними. Тому в задачах конденсації тиск розклинення (як і товщина конденсованого шару) повинен бути змінною залежною величиною.
Розглянемо систему, яка складається з трьох об’ємних фаз “п”, “р” і “т”, а також плівки, що знаходиться між фазами “п” і “т” з поверхневим натягом σпр і σрт. Товщина плівки становить δ. У випадку товстої плівки фаза “ж” знаходиться всередині плівки між поверхневими шарами (рис.8.4). Будемо виходити зі сферичності і симетрії граничних поверхонь. Виділена термодинамічна система вважається закритою, яка непрониклива для маси, але може деформуватися. Через Rnp позначений радіус розділу поверхні на межі “пр”.
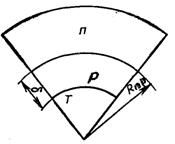
Рис.8.4. Сферична закрита термодинамічна система
Зміна внутрішньої енергії системи визначається як сума відповідних змін енергії її окремих частин:
(8.22)
Стан об’ємних фаз можна описати рівнянням
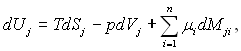(8.23)
де j відповідає “п”, “р”, “т” і і = 1, 2, 3...
Вважаючи усі характеристики твердої фази “т” (і відповідно границі “рт”) незмінними, її можна виключити подальшого розгляду. Тоді, оперуючи для простоти з однокомпонентними фазами (і = 1), можна написати, пропустивши індекс 1:
Підставляючи в (8.22) відповідні значення dUj згідно рівнянню (8.23) і значення dVj , раніше отриманих, приводимо до рівноважного стану систему, яка характеризується рівністю температур і хімічних потенціалів фаз, в наслідок цього отримаємо:
Звідси слідує
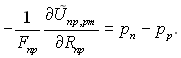(8.24)
Для викривленої плівки за гіббсівського підходу до поняття поверхонь розділу:
(8.25)
Для фіксованого стану поверхні розділу “рт” і при фіксованих фізичних характеристиках викривленого шару
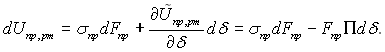(8.26)
Для сферичної границі
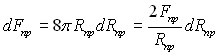
і dδ = dR (див. рис.8.4). Підставляючи у рівняння (8.26) значення dFnp і dδ, отримаємо:
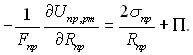(8.27)
Прирівнюючи праві частини рівнянь (8.24) і (8.27), матимемо:
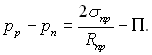(8.28)
У граничному випадку, коли → ∞, П → 0 і рівняння (8.28) переходить у рівняння Лапласа для сферичної поверхні розділу двох об’ємних (масових) фаз “п” і “р”:
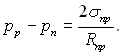(8.29)
Для ввігнутої поверхні pn > pp (Rnp < 0), для випуклої – pр > pп (Rnp > 0).
Згідно рівнянню (8.28) значення різниці тисків в існуючих об’ємних фазах корегується тиском розклинення П. Знак тиску розклинення може бути різним. Для не змочуваної твердої поверхні П < 0, для змочуваної П > 0. У наслідок цього знак різниці рр – рп залежить від знака і абсолютної величини як 2σпр/Rпр, так і П.
Таким чином, урахування взаємодії між поверхневими шарами “пр” і “рт” призводить до зміни умов механічної рівноваги в порівнянні з умовами, які отримуємо при використанні тільки капілярних ефектів першого роду, що виражаються рівнянням (8.29). Вплив капілярних ефектів другого роду повинні сказатися на рівноважному переохолодженні пари.
Розглянемо термодинамічну систему, яка складається з пари і рідкої плівки. Для спрощення середовище вважаємо однокомпонентним. При рівноважному стані хімічні потенціали пари і плівки рівні:
(8.30)
Величини, які стосуються плівки, умовно позначені індексом “р”. У подальшому для скорочення будемо писати μп(рп) і μр(рр).
Для невеликого значення Δр, можна записати наступний ряд:
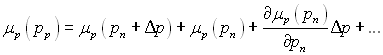
З визначення хімічного потенціалу μ = u + Ts + pυ виходить, що (дμ/др)υ= υ=1/ρ. Враховуючи це співвідношення, отримаємо:
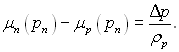(8.31)
Тиск у тонкій викривленій плівці буде відрізнятися від тиску в паровій фазі на величину Δр = (2σпр/Rк) – П (Rк = Rпр при термодинамічній рівновазі). При цьому вважається, що складова П рівномірно розподілена по товщині плівки, чи за іншого підходу, що відповідні значення поверхневих сил віднесені до поверхні плівки у цілому і плівка, маючи надлишкову масу, не має товщини.
Тиску пари рп відповідає температура насичення (для плоскої границі розділу масивних парової і рідкої фаз). Температура Тн(рн) відрізняється від температури фазового переходу 
Вважаємо, що різниця 
порівнянно невелика. Розкладемо
μр(рп) і μп(рп)
в ряд за степенями Δр′ і підставляючи отримані з точністю до другого члена вирази в рівняння (8.31), отримаємо:
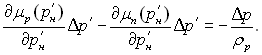(8.32)
При отриманні рівняння (8.32) враховано також, що
Значення похідних, що стоять в лівій частині рівняння (8.32), дорівнюють відповідно 1/ρр і 1/ρп. Ураховуючи це, отримаємо:
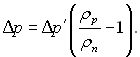(8.33)
Підставляючи значення
1/ρр і 1/ρпр і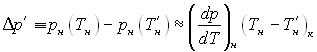 
в рівняння (8.33) і ураховуючи, що згідно закону Клапейрона-Клаузіуса 
матимемо:
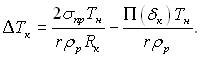(8.34)
Таким чином, критичне (рівноважне) переохолодження пари можна розділити на дві складові частини:
(8.35)
У граничному випадку, коли П → 0, маємо ΔТк,δ = 0 і рівняння (8.35) переходить у формулу Томсона
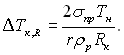(8.36)
У рівнянні (8.35) перша складова обумовлена капілярними ефектами першого роду і відображає вплив кривизни шару. Друга складова
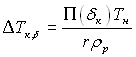(8.37)
виникає внаслідок взаємодії поверхневих шарів. Тут і раніше індексом “к” позначається критичне (рівноважне) значення даної величини. Згідно (8.34) значення Rк і δк взаємозв’язані і при певній величині ΔТк можуть мати різні значення.
З виконаного аналізу слідує, що переохолодження насиченої пари, наприклад, над тонкою не змочуваною плівкою при заданому тиску рн буде більшим, ніж переохолодження над поверхнею масивної рідини при тому ж тиску. Чи теж саме, при заданій температурі Тн пара повинна мати більшу пружність (перенасичення), ніж над масивною рідиною.
Ця обставина пояснюється тим, що поверхневі молекули у плівці зазнають більш слабке притягання з боку внутрішніх молекул, ніж у випадку масивної рідини. Кількість внутрішніх молекул плівки, які взаємодіють з поверхневою молекулою, буде меншою в порівнянні з масивною рідиною. Силове поле, створюване твердою підкладкою, у випадку не змочуваних плівок буде дуже малим.
Внаслідок цього збільшується ймовірність випаровування поверхневих молекул, а значить зростає тиск пари над плівкою. Аналогічне явище має місце і при випаровуванні поверхні розділу двох об’ємних фаз. Останній ефект представлений формулою (8.36).
Розглянемо умови зародження рідкої фази на поверхні тіла. При цьому врахуємо ефекти пов’язані з уявленнями про молекулярну взаємодію поверхневих шарів. При термодинамічній рівновазі згідно (8.31) маємо:
(8.38)
Нехай П < 0. Розглянемо попередньо випадок R → ∞ (Δр = П). Термодинамічний потенціал замкненої системи пара – плоска стінка буде:
(8.39)
Враховуючи, що dMn = –dMp і dMp = ρрFdδ, можна написати наступне рівняння для зміни термодинамічного потенціалу:
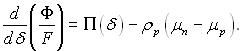(8.40)
У випадку рівноважного стану
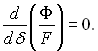
Якщо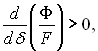 
відбувається випаровування плівки (плівка не може існувати); умова 
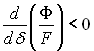відповідає життєздатній плівці (відбувається процес конденсації).
У наслідок цього при рівновазі, як слідує з рівняння (8.40),
(8.41)
що відповідає рівнянню (8.38).
Будемо вважати, що П = Аδ–3, де А – величина, яка не залежить від δ. Графічний розв’язок рівняння ρр(μп – μр) = П(δ) наведений на рис.8.5, де ординати 1, 2 і 3 відповідають різним значенням ρр(μп – μр). Графік до певної міри спрощений в області δ = δ0, де δ0 – товщина стійкого адсорбційного шару, що не має суттєвого значення для виконуваного аналізу.
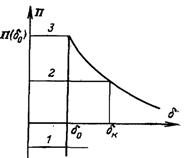
Рис.8.5. Умови термодинамічної рівноваги системи пара – плоска не змочувана плівка: 1 – μп < μp; 2, 3 – μп > μp
У випадку 1, коли μп < μp (ненасичена пара), рівняння ρр(μп – μр) = П задовольняється при єдиному значенні δ = δ0. При цьому величина термодинамічного потенціалу монотонно зростає, тобто плівка з товщиною δ > δ0 не повинна утворюватися.
Для пересиченої пари (μп > μp ) за умови 0 < ρр(μп – μр) < П(δ0) рівняння ρр(μп – μр) = П(δ) має корні δ0 і δк (ордината 2). Значенню δ0 відповідає мінімум Ф(δ), а значенню δк – максимум Ф(δ). У відповідності із загальними умовами термодинамічної рівноваги стан системи з плоскою плівкою товщиною δк буде метастабільним, тобто стійким по відношенню до безмежно малих змін, але нестійким по відношенню величин з кінцевими значеннями. Плівка повинна бути здатною до подальшого росту тільки за умови δ > δк.
Якщо ρр(μп – μр) ≥ П(δ0) термодинамічний потенціал Ф(δ) монотонно зменшується з ростом товщини плівки. При цьому на поверхні відбувається конденсація пари.
Для того щоб утворилася плоска плівка з товщиною δ < δк, спроможна до подальшого росту, необхідно подолати потенціальний бар’єр
Очевидно, значення цього бар’єру зменшується з ростом пересичення пари (μп – μр) і перетворюється в нуль при ρр(μп – μр) = П(δ0).
Зроблені висновки справедливі для плоскої плівки. У реальних умовах поверхня тіла не є абсолютно однорідною. Навіть при високих класах чистоти середньоквадратична величина мікронерівностей (виступів) буде становити 0,05...1,6 мкм, тобто співрозмірна зі значеннями R, які відповідають інтервалу найкращої погодженості формули Томсона (0,1...1,0 мкм). При цьому локальні значення радіусів мікрошорсткості можуть змінюватися у широких межах.
Для урахування кривизни плівки величину Δр представимо як
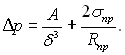
Розглянемо умови утворення плівки на сферичній випуклості твердого тіла. Під час росту плівки змінюється не тільки її товщина, але і радіус Rпр. У цьому випадку dδ = dRnp і Rnp = δ +(R0 – δ0), де R0 – радіус поверхні стійкого адсорбційного шару товщиною δ0. Величина Rm = R0 – δ0 відповідає радіусу виступу твердого тіла. Виконавши заміну Rnp = δ + Rm отримаємо:
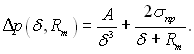(8.42)
Функція Δр(δ) для викривленої плівки залежить від параметра Rm.
З рівняння (8.42) виходить, що
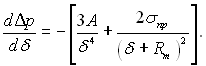(8.43)
При δ→∞ dΔp/dδ→0 незалежно від величини Rm. При δ→δ0 (δ >δ0) кривизна Δp = Δp(δ) змінюється все більше, збільшуючись зі зменшенням радіуса Rm випуклості твердого тіла. Криві Δp(δ) розміщуються над кривою, яка відповідає випадку R→∞.
Для ввігнутої поверхні твердого тіла dδ = –dRnp і Rnp = –(δ + Rm). Криві Δp(δ) розміщуються нижче кривої, яка відповідає плоскій пластині. Кривизна зростає зі збільшенням Rm.
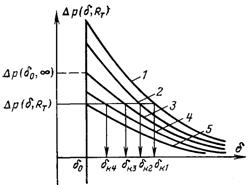
Рис.8.6. Умови термодинамічної рівноваги системи пара – викривлена не змочувана плівка
Графіки залежності Δp = Δp(δ, Rm) наведені на рис.8.6. Крива 3 відповідає плоскій пластині. Над нею розміщуються криві 1, 2 для випуклої плівки, нижче, криві 4, 5 – для ввігнутої. Чим далі знаходяться відповідні криві Δp(δ, Rm) від кривої Δp(δ,∞), тим менше значення радіуса Rm їм відповідає.
Як слідує з рис.8.6 критичні значення товщини плівки, а значить і потенціальний бар’єр, подолання якого необхідне для утворення життєздатної плівки, за інших рівних умов менше у випадку утворення зародка на ввігнутому тілі. Наприклад, для радіуса ввігнутості Rm5, який відповідає кривій 5, потенціальний бар’єр при заданій різниці тисків Δp(δ, Rm) стає рівним нулю і δ05 = δк5. При Rm < Rm5 потенціальний бар’єр стає від’ємним.
Таким чином, за інших різних умов термодинамічна найбільша ймовірність виникнення зародка у ввігнутостях (западинах) твердого тіла. Якщо допустити, що 
то у западинах може конденсуватися ненасичена пара (капілярна конденсація).
Використовуючи рівняння (8.33) і (8.34), можна перейти від пересичення пари Δp до його переохолодження ∆Тк. З причини малого термодинамічного опору зародкових утворень конденсату переохолодження можна ототожнювати з температурним напором ∆Т = Тн – Тст. Очевидно, виводи зроблені стосовно впливу Δp, якісно можна розповсюдити при використанні величини ∆Т.
При конденсації пари органічних речовин (особливо неполярних) величина Δp до його переохолодження ∆Тк. З причини малого термодинамічного опору зародкових утворень конденсату переохолодження можна ототожнювати з температурним напором ∆Т = Тн – Тст. Очевидно, виводи зроблені стосовно впливу Δp, якісно можна розповсюдити при використанні величини ∆ТТк мала. У цьому випадку ймовірність зародкового утворення конденсату збільшується.
Інший граничний випадок має місце при конденсації металевої пΔp до його переохолодження ∆Тк. З причини малого термодинамічного опору зародкових утворень конденсату переохолодження можна ототожнювати з температурним напором ∆Т = Тн – Тст. Очевидно, виводи зроблені стосовно впливу Δp, якісно можна розповсюдити при використанні величини Тари, наприклад пари ртуті на окисленій металевій поверхні. Розрахунки показують, що значення ∆Тк,δ для ртуті більш ніж на порядок перевищують значення ∆Тк,δ для води. З цієї причини утворення плівок ртуті критичної товщини утруднене.
Проміжне положення займає випадок конденсації води на гідрофобних поверхнях.
