8.3. Швидкість росту тонкої плівки конденсату

Розглянемо конденсацію однокомпонентної насиченої пари. Виділимо у парі біля поверхні конденсату кнудсенівський шар, тобто шар товщиною ℓ, рівний за порядком середній довжині вільного пробігу молекул (рис.8.7). Через Т_п і Т_пов позначимо відповідно температуру пари на зовнішній границі кнудсенівського шару і температуру поверхні рідини.

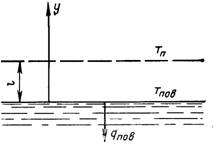
Рис.8.7. Кнудсенівський шар

Потік пари, що проходить крізь зовнішню границю кнудсенівського шару по напрямку до поверхні рідини, дорівнює тп_пс(_уп, від рідини у пару тп_повс(_упов, де с(_у – нормальна до поверхні рідини складова середньої теплової швидкості молекул; п – кількісна концентрація молекул, м^–3; т – маса молекули. Результуючий потік маси j, віднесений до одиниці поверхні, можна представити в першому наближенні наступною формулою:

(8.44)

де f – коефіцієнт конденсації. За визначенням коефіцієнт конденсації це відношення числа захоплених по верхньою рідини молекул до загальної кількості молекул пари, які падають на поверхню конденсату:

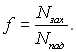(8.45)

У загальному випадку коефіцієнт конденсації може змінюватися від 0 до 1.

Для максвелівського розподілу молекул за швидкостями можна написати:

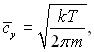
де k = 1,38·10^–23 Дж/К – стала Больцмана. Підставляючи в рівняння (8.44) значення с(_у і п = р/kT, взяті відповідно за температурами Т_п і Т_п.пов, матимемо:

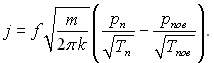(8.46)

У цьому рівнянні Т_п і Т_пов – відповідно температура пари і поверхні конденсату; р_п(Т_п) і р_пов(Т_пов) – тиск насичення відповідно при температурах Т_п і Т_пов.

Формула (8.46), називається формулою Герца-Кнудсена, отримана для порівняно простої моделі, в якій не робляться відмінності між розподілом швидкості молекул, які рухаються до рідині і від неї.

Для первинної оцінки тепло переносу через тонку плівку обмежимося більш простою моделлю. З формули (8.46) виходить, що при j і f не рівних нулю на границі пара – рідина має місце стрибок температури ΔТ_ст = Т_п – Т_пов. Існування різниці температур ΔТ_ст. дозволяє (хоч і формально) ввести поняття термічного опору R_ф:

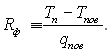(8.47)

Вважаючи, що теплота q_пов, Вт/м², яка переноситься через фазову поверхню, є тільки теплота фазового переходу, маємо q_пов = jr. Тоді можна написати, з урахуванням (8.46) і (8.47):

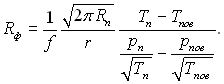(8.48)

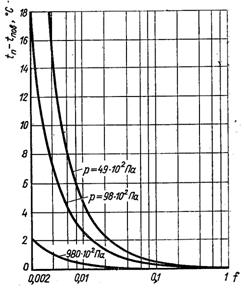
Рис.8.8. Вплив коефіцієнта конденсації і тиску пари на стрибок температур Т_п – Т_пов при q = 29 кВт/м²

Розрахунки за формулою (8.48) показують, що чим менший тиск пари і коефіцієнт конденсації і чим більший q_пов, тим більший температурний стрибок. На рис.8.8 наведені значення стрибка температур Т_ст в залежності від тиску водяної пари, що конденсується і значення коефіцієнта конденсації f при q_пов ≈ 29000 Вт/м². Як слідує з рисунка при певних умовах температурний стрибок може бути значним.

В умовах термодинамічної рівноваги згідно (8.31)

Відомо, що при цьому

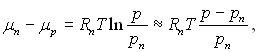
де р і р_п – відповідно тиск насичення над скривленою плівкою і плоскою границею масової рідини при температурі Т_п; R_п – газова стала пари.

Звідси виходить, що

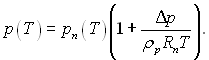(8.49)

Згідно виводів в § 8.2, можна записати:

де р_σ = 2_σпр/R_пр. Член 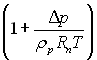відіграє роль поправки на величини δ і R_пр.

Підставляючи значення р(Т_пов) згідно рівнянню (8.49) у формулу (8.46) і помноживши її ліву і праву частини на r, отримаємо для порівнянно невеликої різниці температур:

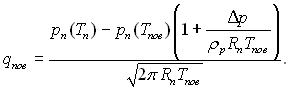(8.50)    

Це рівняння можна переписати в наступному виді:

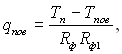(8.51)

де

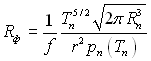(8.52)    

– термічний опір на плоскій межі розділу пара – масивна рідина. Множник R_ф1 відіграє роль певної поправки, введення якої обумовлено особливими властивостями тонкої викривленої плівки:

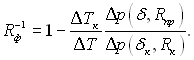(8.53)

При Т_п – Т_пов > ΔТ_к величина R_ф1 знаходиться біля одиниці, якщо δ >>δ_к і R_пр>>R_к. У випадку, коли R_пр→ ∞ (плоска стінка), маємо:

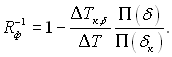(8.54)

Згідно останньої формули величина R_ф1 близька до одиниці починаючи з товщини плівки δ = 2δ₀, оскільки другий доданок у формулі (8.54) зменшується зворотно пропорційно кубу товщини плівки. Величина R_фf, м²·К/Вт, наводиться нижче при різних температурах насичення Т_п води:

З урахуванням термічного опору теплопровідності плівки для повного термодинамічного опору переносу теплоти від пари до стінки можна написати в першому наближенні наступне рівняння:

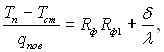
де Т_ст – температура поверхні стінки; δ – товщина плівки; λ – коефіцієнт теплопровідності плівки, рівний в першому наближенні коефіцієнту теплопровідності масивної рідини. Із співставлення величин R_ф1R_ф і δ/λ, виходить, що при конденсації водяної пари атмосферного тиску термічний опір плівки стає суттєвим, починаючи з товщини приблизно 10^–7 м.

Розрахунок міжфазного термічного опору часто затрудняється із-за з причини відчутності повної інформації про значення коефіцієнта конденсації за різних умов. Необхідно також урахувати, що при дослідному визначенні f його величина є похідною від вибору для опрацювання дослідних даних відповідної формули. Це особливо проявляється, коли f → 1. На підставі опрацювання дослідних даних Д.О.Лабунцовим було показано, що коефіцієнт конденсації є функцією тиску. При низьких тисках він близький до одиниці, в області високих тисків коефіцієнт конденсації зменшується.

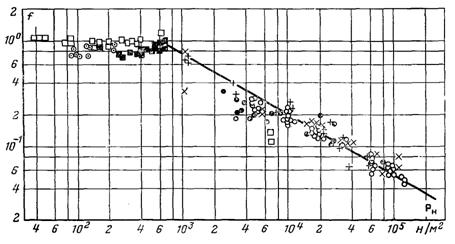
Рис.8.9. Залежність коефіцієнта конденсації від тиску пари

В результаті опрацювання дослідних даних багатьох науковців для води і металів (калій, натрій, ртуть) за формулою (8.52), але з введенням замість 1/f функції (2 – f)/2f, отримано графічну залежність наведену на рис.8.9. З рисунка слідує, що в області тисків 700 ≤ р_п ≤ 10⁵ Па коефіцієнт конденсації суттєво залежить від тиску. Залежність f(р_п) апроксимується рівнянням:

(8.55)

де р_п виражається в Па.

В області порівнянно низьких тисків (р_п < 700 Па) коефіцієнт конденсації практично дорівнює одиниці.