Розділ 9. КРАЙОВІ ЗАДАЧІ ТЕПЛОМАСООБМІНУ ПРИ КОНДЕНСАЦІЇ

9.1. Диференціальні рівняння

Процеси теплообміну при конденсації пари відбуваються в системах, які складаються по крайній мірі з двох співіснуючих фаз: пари (парогазової суміші чи суміші парів) і конденсату, який може знаходитися в рідкому чи твердому стані. У теплообмінних пристроях рекуперативного типу конденсат утворюється на охолоджувальних твердих стінках. Внаслідок цього в загальному випадку задачі теплообміну при конденсації відносяться до спряжених задач, в яких процеси теплообміну, що відбуваються в суміжних фазах, взаємозв’язані.

Існуючі фази можуть бути як однокомпонентними, так і багатокомпонентними. Ми обмежимося розглядом систем, що складаються з одно- і двокомпонентних рухомих фаз. Гідродинамічний і тепловий стан фаз вважається визначеним, якщо відомі поля температури Т (чи питомої ентальпії h), швидкості w, тиску р і концентрації компонентів т_і як функції часу і координат х, у і z. Для знаходження цих полів використовується феноменологічний метод, в якому вважають, що співіснуючі фази є суцільними середовищами і при їх розгляді можна не звертати увагу на мікроструктуру речовини.

Для знаходження полів перелічених фізичних величин використовуються диференціальні рівняння енергії, руху, суцільності потоку і дифузії (масообміну), вивід яких ґрунтується на фундаментальних законах збереження енергії, кількості руху і маси. Вивід цих рівнянь приводиться в багатьох літературних першоджерелах, і тому в подальшому будемо наводити рівняння без виводу.

Рівняння енергії для однокомпонентної ізотропної рідини зі змінними фізичними властивостями, яке враховує перенос теплоти теплопровідністю і конвекцією можна записати так:

(9.1)

де h – ентальпія рідини, віднесена до одиниці маси; Т – температура; р – тиск; ρ – густина; λ – коефіцієнт теплопровідності; q_υ – потужність внутрішніх джерел теплоти; μФ – дисипативна функція. Члени рівняння (9.1) вимірюються у Вт/м³. Субстанційні похідні dh/dτ і dp/dτ  визначаються згідно виразу

(9.2)

Дисипативна функція, введена Релеєм враховує розсіювання енергії, при ньютонівському законі тертя має вигляд:

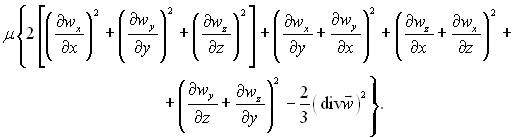(9.3)

У реальних рідин h = h(р, Т), тобто

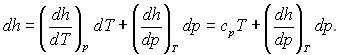
Тому що

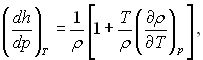
то

(9.4)

де 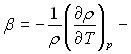термічний коефіцієнт об’ємного розширення.

Підставляючи (9.4) в рівняння (9.1), отримаємо:

(9.5)

де с_р – ізобарна теплоємність, віднесена до одиниці маси.

Для крапельних рідин значення β мале (β→0). Для термодинамічно-ідеальних газів β =1/Т, тобто βТ = 1. Якщо рідина рухається зі швидкістю набагато меншою швидкості звуку, і дисипація механічної енергії несуттєва, рівняння (9.5) можна записати в наступному вигляді:

(9.6)

При w = 0 рівняння (9.6) переходить у рівняння теплопровідності

(9.7)

Якщо можна знехтувати несталістю фізичних параметрів, то рівняння (9.6) приводиться до вигляду

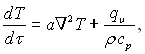(9.8)

де а = λ/ρс_р  – коефіцієнт температуропровідності. Рівняння енергії у формі (9.8), як і більш повні його вирази, записане для хімічно однорідних середовищ.

У випадку багатокомпонентної суміші необхідно враховувати перенос ентальпії молекулярною дифузією. В рідинах цей процес несуттєвий і зазвичай не враховується. У газових сумішах він відбувається інтенсивніше, але і у цьому випадку ця величина в багатьох задачах може бути незначною у порівняння з переносом теплоти конвекцією і теплопровідністю.

Для бінарної суміші з урахуванням переносу ентальпії тільки концентраційною дифузією, при dp/dτ = 0  і нехтуючи дисипацією механічної енергії, рівняння (9.1) можна записати в наступному виді

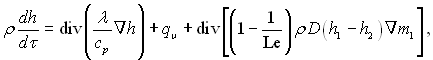(9.9)

де h, h₁, h₂ – відповідно ентальпії суміші, першого і другого компонентів, віднесені до одиниці маси; Le = ρc_pD/λ – число Льюіса – Семенова; D – коефіцієнт дифузії; ρ, c_p, λ  – відповідно густина, ізобарна теплоємність і коефіцієнт теплопровідності суміші.

При записі останнього рівняння вважається, що можна використати закон Фіка, наведений у такій формі:

(9.10)

де т₁ = ρ₁/ρ; ρ₁  – густина маси першого компоненту.

Рівняння руху рідини зі змінними фізичними властивостями, підпорядковуються узагальненому ньютонівському закону в’язкого тертя у виді

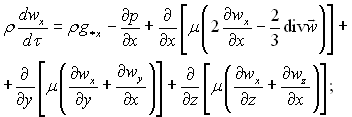(9.11)

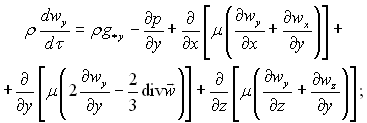(9.12)

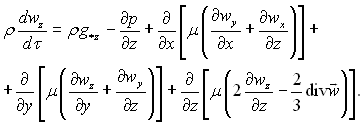(9.13)

Субстанціальні похідні /dτ, dw_у/dτ і dw_z/dτ  визначаються згідно (9.2). У рівняннях руху (9.11)...(9.13) μ  – динамічний коефіцієнт в’язкості; g*_x, g*_у і g*_z – проекції вектора прискорення зовнішніх масових сил на відповідні осі декартових координат; р – тиск.

Якщо коефіцієнт в’язкості постійна величина, рівняння (9.11)...(9.13) можна переписати наступним чином:

(9.14)

Для нестисливих рідин div w = 0, і рівняння (9.14) набуває вигляд:

(9.15)

При неоднорідному розподілі густини за об’ємом фази необхідно враховувати виникаючу змінність масової сили. Члени можна представити в наступному виді:

де ρ₀ – густина рідини у фіксованій точці розглядуваної фази у фіксований час.

Змінність густини може виникати внаслідок неоднорідності полів температури, тиску, концентрації компонентів суміші. Змінність масової сили може бути обумовленою неоднорідністю поля зовнішніх масових сил (наприклад, в обертальній системі, в електромагнітному полі). У подальшому в основному вважатимемо, що , де – прискорення вільного падіння. У технічних пристроях може бути функцією часу, але незмінною в розглядуваній області величиною.

Різницю можна представити у вигляді де р₁ = р – р₀ (р₀ –гідростатичний тиск). При підстановці у рівняння руху індекс 1 зазвичай випускають, розуміючи при цьому, що величина р у неявному виді включає в себе і гідростатичний тиск.

Рівняння суцільності потоку для стисливої рідини має вид:

чи, що те ж саме,

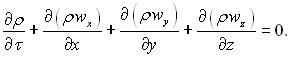(9.16)

Якщо ρ = const, то

(9.17)

Рівняння масообміну (рівняння збереження маси і-го компоненту) стосовно до умов, для яких записане рівняння енергії (9.9), може бути представлене в наступному виді:

(9.18)

Записуючи рівняння (9.18) вважали, що молекулярний перенос і-го компоненту здійснюється тільки концентраційною дифузією, яка описується законом Фіка. Рівняння (9.18) буде несправедливе, якщо в рідині відбуваються хімічні реакції, які ведуть до створення (зникнення) і-го компоненту. В останньому випадку до правої частини рівняння необхідно добавити член j_υi, кг/(м³·с), який враховує виникнення (зникання) маси і-го компоненту. Величина j_υi описується рівняннями хімічної кінетики і для заданого складу є функцією температури і тиску.

Якщо величини λ, с_р, ρ, μ і D при розв’язку задачі вважаються змінними, і є функціями температури Т = Т(τ, х, у, z), то до диференціальних рівнянь енергії, руху, суцільності потоку і масообміну необхідно добавляти рівняння виду λ=λ(Т), с_р=с_р(Т)і т. д. У цьому випадку перераховані фізичні величини є залежними змінними. І тоді можна говорити про існування полів не тільки Т, w, р, т_і, але і полів λ, с_р, ρ, μ і D.

Очевидно, що при математичному формулюванні крайової задачі кількість залежних змінних повинна дорівнювати кількості рівнянь. Система диференціальних рівнянь записується для кожної окремої фазової області. Для конкретизації задачі повинні бути задані крайові умови, які характеризують значення шуканих функцій чи їх похідних при граничних просторових і часових значеннях невідомих параметрів τ, х, у, z.

За наявності у досліджуваній системі декількох взаємодіючих фаз крайові умови для окремих фаз часто не можуть бути задані наперед. У цьому випадку крайові умови наперед призначаються тільки на часових і просторових границях досліджуваної системи співіснуючих фаз. Всередині системи на фазових границях призначаються так звані умови спряження, які установлюють характер зв'язку полів Т, w та ін. в суміжних фазах. Наприклад, в умовах спряження може призначатися рівність швидкостей, температур і теплових потоків на фазових границях (чи розрив в значеннях залежних змінних чи їх похідних на фазових границях). Значення залежних змінних на фазових границях зазвичай підлягають визначенню під час вирішення задачі.

Для призначення крайових умов і умов спряження необхідні знання принципових особливостей взаємодії фаз (див. § 9.2).

При плівковій конденсації товщина шару конденсату δ зазвичай невелика у порівнянні з його довжиною ℓ. Умова  δ << ℓ  дозволяє спростити систему диференціальних рівнянь, записавши її для шару конденсату в наближені пограничного шару. Якщо пара має достатньо велику повздовжню складову швидкості, то у парі біля поверхні плівки також утворюється пограничний шар. Для стаціонарного плоского пограничного шару рівняння руху, нерозривності потоку, енергії можна записати в наступному виді:

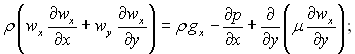(9.19)

(9.20)

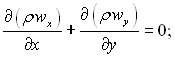(9.21)

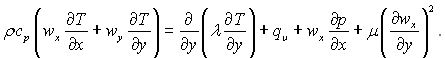(9.22)

Для стаціонарного плоского пограничного шару при усталених фізичних властивостях ρg_x = 0, др/дх = 0, q_υ = 0, і нехтуючи дисипацією механічної енергії ці рівняння записуються так:

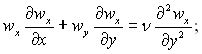(9.23)

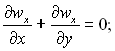(9.24)

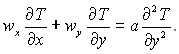(9.25)

Задовольняючи рівняння нерозривності потоку, можна записати:

(9.26)

де ψ – функція незалежних змінних (функція току).

Підставляючи значення w_x і w_y з рівнянь (9.26) в (9.24) отримуємо тотожність. Введемо нову змінну у/δ, де δ  величина порядку 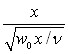; w₀, ν – характерні значення швидкості і кінематичного коефіцієнта в’язкості. Тоді нова змінна η буде:

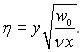(9.27)

Введемо також безрозмірну функцію току f(η) згідно рівнянню

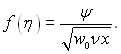(9.28)

З (9.26) і (9.28) виходить, що

і

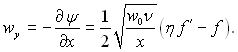
Підставляючи ці вирази складових швидкостей w_x і w_y в рівняння руху пограничного шару (9.23), отримаємо:

чи

(9.29)

тобто звичайне диференціальне рівняння.

Аналогічним чином можна перетворити і рівняння енергії пограничного шару (9.25). В результаті чого матимемо:

(9.30)

У цьому рівнянні Θ(η) = θ/θ₀; θ – надлишкова температура; θ₀ – характерна різниця температур; Pr = μc_p/λ.