




9.2. Умови взаємодії фаз
Розглянемо замкнений об’єм V, який складається з двох фаз 1 і 2 з об’ємами відповідно V1 і V2 (рис.2.1).
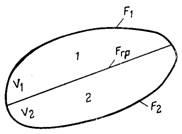
Рис.9.1. Двофазна система: 1 – перша фаза; 2 – друга фаза
Поверхня Fгр, що ділить фази є непроникливою (результуючий потік маси відсутній). Зовнішня поверхня F об’єму складається з частин F1 і F2. Об’єм V і його складові частини V1 і V2 є довільно виділеними і деформованими об’ємами. Згідно з принципом Даламбера під час руху будь-якої матеріальної системи у кожний момент часу сили, які прикладені до неї, включаючи і сили інерції, взаємно врівноважені. Додаючи сили за об’ємом V = V1 + V2, отримаємо:
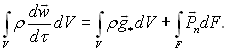 (9.31)
(9.31)
Ліва частина рівняння (9.31) враховує сили інерції, перший член правої частини – масові сили, обумовлені зовнішніми силовими полями (зовнішні масові сили); другий член – поверхневі сили, які є наслідком дії зовнішніх до розглядуваної системи об’єктів (зовнішні поверхневі сили); Рп – вектор напруги поверхневих сил, прикладений до площадки dF по нормалі п. Додатним напрямком п вважається напрямок вектора від розглядуваного об’єму.
Окремо для фаз 1 і 2 можна написати:
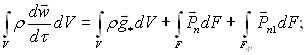 (9.32)
(9.32)
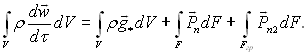 (9.33)
(9.33)
Після додавання рівнянь (9.32) і (9.33) і віднімання з отриманої суми рівняння (9.31) отримаємо:
![]() (9.34)
(9.34)
У зв'язку з тим, що об’єми V, V1, V2 і поверхні Fгр вибрані довільно, можна записати:
![]()
Вектор Рп у загальному випадку довільно орієнтований до площини dF з нормаллю п, можна розкласти на складові Рпп і Рпt, відповідно співпадаючі з напрямком нормалі п і напрямком дотичної t до поверхні елемента dF. Тоді
![]() (9.36)
(9.36)
і
![]() (9.37)
(9.37)
Рівняння (9.35) повинно виконуватися на непроникливій поверхні розділу фаз.
Подумки уявимо краплю рідини зі сферичною поверхнею радіуса R, завислу в насиченому парі з тиском рп. Конденсація чи випаровування відсутні – система знаходиться у термодинамічній рівновазі. У цьому випадку до поверхні краплі прикладені тільки нормальні сили, спрямовані по радіусу і незмінні по поверхні. Згідно рівнянню Лапласа (8.29) тиск у краплі рр відмінний від тиску в парі на величину рσ = 2σпр/R. Тобто, має місце стрибок тиску рр – рп. Але в даному простому прикладі на границі розділу фаз завжди виконується умова
(рр)1 = (рп + рσ)2
чи
(рр – рσ)1 = (рп)1,
тобто нормально прикладені до сферичної поверхні розділу фаз тиски взаємно врівноважуються. Дотичні напруги у цьому прикладі дорівнюють нулю.
У більш загальному випадку, наприклад під час руху краплі в парі, крім капілярних необхідно враховувати і інші сили такі , які викликані динамічною взаємодією пари і рідини. Розподіл нормальних і дотичних напруг по поверхні розриву буде при цьому неоднорідною. Крапля може випаровуватися чи рости за рахунок конденсації.
При переносі маси крізь границю розділу фаз (конденсація, випаровування) рівність (9.35) порушується.
Рис.9.2. Вектор wгр
Зазвичай при дослідженні задачі про конденсацію, систему координат зручно прив’язувати до фіксованої точки тієї фази, яка не підлягає деформації, наприклад до осі симетрії труби, на поверхні якої відбувається конденсація. У цьому випадку поверхня розриву конденсат – пара може змінюватися в даній системі координат в часі і просторі, тобто бути функцією τ, х, у і z. Швидкість переміщення в просторі поверхні розриву у кожній точці може характеризуватися вектором швидкості wгр нормальним до фазової поверхні (рис.9.2).
Швидкість wгр у кожній точці поверхні розриву буде дорівнювати нулю, якщо границя не змінюється в часі. Очевидно також, що вектор швидкості wгр залежить також від вибору системи координат. Можна вибрати таку систему координат, зв’язану з елементом поверхні розриву dF, що швидкість wгр буде дорівнювати нулю в даній точці. Але при цьому у сусідніх точках при довільній зміні поверхні розриву швидкість wгр ≠ 0.
Будемо дотримуватися наступного правила нумерації сторін поверхні розриву: напрямок нормалі до dF повинен відповідати переходу з боку фази 2 на сторону фази 1.
Нехай на фазовій границі відбувається конденсація пари чи рівномірне відсмоктування конденсату в стінку. Фазу, яка конденсується чи відсмоктується позначаємо індексом 1. За одиницю часу через одиницю фазової поверхні нормально до неї проходить маса в кількості jгр1. Локальна нормальна складова швидкості фази 1 на границі розриву
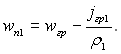 (9.38)
(9.38)
У фазі 2 на цій же границі локальна нормальна складова швидкості буде:
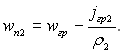 (9.39)
(9.39)
У відповідності із законом збереження маси при переході через границю фаз маємо jгр1 = jгр2 = jгр. Тоді з (9.38) і (9.39) виходить, що
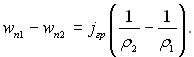 (9.40)
(9.40)
Згідно рівнянню (9.40) при ρ1 ≠ ρ2 на поверхні розриву має місце не тільки стрибок густини, а і стрибок нормальної складової швидкості (wn1 – wn2 ≠ 0). Цей стрибок обумовлений переносом маси через фазову границю. Якщо jгр = 0, то
wn1 = wn2 , (9.41)
тобто на границі розділу фаз складова швидкості безперервна.
З рівнянь (9.38) і (9.39) виходить також, що
![]() (9.42)
(9.42)
Рівняння збереження маси (9.42) при wгр = 0 переходить в очевидне співвідношення ρ1wn1 = ρ2wn2 чи jгр1 = jгр2. Разом з масою через фазову границю переноситься кількість руху jгрw. У наслідок цього для поверхні розриву справедлива умова
![]() (9.43)
(9.43)
У разі, коли wгр = 0, то з (9.43) слідує, що
![]()
чи
![]() (9.44)
(9.44)
Згідно останнього рівняння рівнодіюча векторів напруг, прикладених до елементу поверхні розриву, дорівнює реактивній силі, обумовленій переходом маси через фазову границю.
На підставі досліджень, у механіці суцільних середовищ зазвичай вважають, що на границі розділу двох суцільних середовищ тангенціальні складові швидкості рівні: wt1 = wt2 . (9.45)
Цю умову часто називають умовою адгезії (прилипання). При виконанні рівностей (9.41) і (9.45) маємо що на поверхні розриву
w1 = w2 . (9.46)
У загальному випадку
wt1 = wt2 + ∆wст, (9.47)
тобто має місце стрибок дотичної складової швидкості (ковзання фаз). Стрибок швидкості чи швидкість ковзання ∆wст залежить від густини потоку маси, який проходить крізь фазову границю. У граничному випадку ∆wст може прямувати до нуля.
З механіки суцільних середовищ слідує, що локальну енергетичну взаємодію на границі розділу фаз можна описати наступним рівнянням
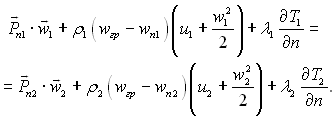 (9.48)
(9.48)
Перші члени лівої і правої частини рівняння (9.48) ураховують роботу поверхневих сил і представляють собою скалярний добуток векторів Рп і w. Другі члени – перенос внутрішньої і кінетичної енергії з масою, що проходить крізь між фазну границю. Останні – перенос теплоти теплопровідністю.
У деяких задачах останні члени лівої і правої частин рівняння (9.48) необхідно заміняти на q*, де q* густина потоку енергії при урахуванні зовнішнього потоку енергії як теплової, так і нетеплової природи (у тому числі роботи поверхневих моментів та ін.); потік енергії q* (включаючи теплопровідність) означає додатковий приток енергії в порівнянні з притоком механічної енергії, обумовленої роботою масових і поверхневих сил.
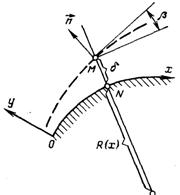
Рис.9.3. До плоско паралельного омивання поверхні двофазним потоком
Розглянемо плоско паралельне омивання поверхні тіла двофазним потоком. Проведемо до вибраних точках обтічного контуру (рис.9.3) нормалі до нього. Нехай нормаль через довільну точку М, яка лежить на поверхні розриву біля контуру, пересікає його у точці N. Положення точки М будемо визначати значеннями х і у = δ(х) – значення довжини дуги кривої ON і відрізка нормалі NM.
Позначимо через β кут між напрямком лінії розриву у деякій її точці і дотичною до контуру в точці з тією ж координатою х. Тоді
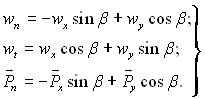 (9.49)
(9.49)
Для ламінарного режиму руху в’язкої рідини складові рхх, рху, руz векторів сили тиску Рх і Ру виражаються формулами:
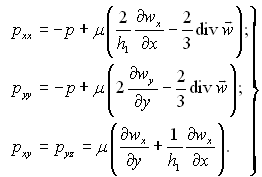 (9.50)
(9.50)
У цьому рівнянні р – тиск; μ – коефіцієнт динамічної в’язкості; h1=1+δ/R(x) – коефіцієнт Ляме; R(x) – радіус кривизни контуру.
Використовуючи (9.49) і (9.50), рівняння кількості руху (9.43) і енергії (9.48) можна записати в компонентах швидкості. Вважаємо, що число Рейнольдса Re = w0ℓ/ν, де w0 і ℓ – характерні значення швидкості і довжини, прямує до нескінченності. Останнє дозволяє використати наближення в пограничному шарі. Інші величини (wx, wy, p, ρ, μ, T, β) і їх похідні мають кінцеві значення. Внаслідок цих допущень для поверхні розриву можна отримати наступні рівняння:
рівняння нерозривності потоку
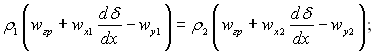 (9.51)
(9.51)
рівняння кількості руху (9.43) в проекції на нормаль до поверхні розриву
р1 = р2 (9.52)
(точніше, у розглядуваному випадку тиск у суміжних фазах на поверхні розриву відрізняється на величину σ12/R).
З рівняння (9.43) в проекції на дотичну до поверхні розриву
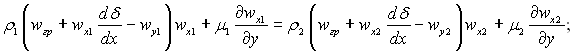 (9.53)
(9.53)
Рівняння енергії для поверхні розриву (9.48) набуває наступного вигляду:
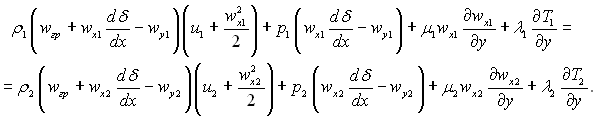 (9.54)
(9.54)
Використавши рівняння (9.51) і (9.52) і враховуючи теорему кількості руху, рівняння (9.54) можна записати в наступному вигляді:
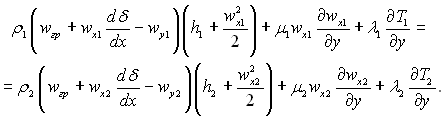 (9.55)
(9.55)
У цьому рівнянні h – ентальпія одиниці маси.
Якщо вважати, що похідна dδ/dx має мале значення (tgβ → 0), то для стаціонарної задачі при повільному русі нестиглого середовища умова (9.55) набуває простого вигляду:
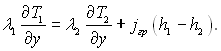 (9.56)
(9.56)
Згідно (9.56) на границі розриву має місце стрибок теплового потоку λ(дТ/ду) на величину другого члена правої частини, якщо jгр ≠ 0 і h1 ≠ h2. Крім теплопровідності теплота переноситься разом з масою речовини, яка проходить крізь фазову границю.
У тих випадках, коли потік маси через між фазну поверхню відсутній, тобто коли wгр = wn1 = wn2 (наприклад на непроникливій поверхні твердого тіла), рівняння (9.42) тотожно рівне нулю, а рівняння (9.43) переходить в
Рп1 = Рп2,
що дає 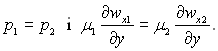 (9.57)
(9.57)
Ураховуючи, що wгр = wу1 = wу2 і tgβ = 0, рівняння (9.48) можна записати в такому виді:
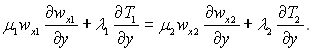 (9.58)
(9.58)
Якщо w1 = w2 то рівняння (9.58) приводиться до рівності:
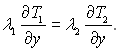 (9.59)
(9.59)
Останнє рівняння зазвичай виконується на фазовій границі конденсат – стінка. При λ1 ≠ λ2 на між фазній границі відбувається розрив градієнту температури.
Розподіл температури на фазовій границі може здійснюватися безперервно, тобто
Т1 = Т2, (9.60)
чи (у випадку омивання конденсату парою низького тиску і при великих поперечних потоках маси) терпить розрив:
Т1 = Т2 + ΔТст.. (9.61)
При омиванні поверхні конденсату парою рівняння (9.60) можна вважати граничним випадком рівняння (9.61).
Розв’язок задач течії і теплообміну в газовому середовищі виконується із залученням кінетичної теорії газів. При досить малих числах Кнудсена Kn = ℓ|/ℓ0, де ℓ| – середня довжина вільного пробігу молекул; ℓ0 – характерний розмір. Розв’язок кінетичного рівняння Больцмана можна отримати апроксимаційним рішенням в нав’є-стоксівському наближені, яке відповідає суцільному середовищу. Але за будь-якого малого значення числа Кнудсена біля фазової границі є область, де течія не описується нав’є-стоксівським наближенням. Товщина цієї області, яка називається шаром Кнудсена, має порядок характерної довжини пробігу ℓ|.
У загальному випадку функція розподілу молекул біля поверхні, тобто на внутрішній границі кнудсівського шару, відмінна від рівноважної максвелівської, і число молекул, які падають на поверхню, не визначається концентрацією, а залежить від усіх параметрів, які визначають течію в кнудсівському шарі. Виняток становить повільна конденсація, коли з достатньою точністю можна знехтувати відхиленням від максвелівського розподілу.
Рівновага може бути порушена не тільки відхиленням концентрації біля стінки від рівноважної, але і іншими причинами, які відхиляють рівновагу молекул за швидкостями в кнудсівському шарі від максвелівської, наприклад наявністю теплового потоку.
При вирішенні задач гідродинаміки і теплообміну в рамках теорії суцільного середовища приходиться установлювати такі фіктивні макроскопічні граничні умови на поверхні розділу фаз, за яких рішення поза кнудсівським шаром співпадало б з рішенням рівняння Больцмана із заданими дійсними умовами на стінці.
Припустимо, що швидкість фазової границі дорівнює нулю. У цьому випадку за будь-якого закону відбиття молекул (окрім повністю дзеркального) повинно відбуватися гальмування газу на поверхні розділу фаз. З іншого боку, немає підстав вважати швидкість газу біля стінки рівною швидкості поверхні. Аналогічно немає підстав вважати температуру пари біля границі рівною температурі поверхні.
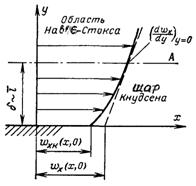
Рис.9.4. До визначення граничних умов
На рис.2.4 суцільною кривою зображена зміна дійсної швидкості газу біля стінки. Штрих пунктирна границя А виділяє шар Кнудсена і область, в якій кінетичне рівняння Больцмана з достатньою точністю описується нав’є-стоксівським наближенням, тобто з позиції механіки суцільного середовища. Якби були відомі швидкість і температура границі кнудсівського шару, то розподіли wx(x, y) і Т(х, у) могли б бути знайдені у всій зовнішній, по відношенню до шару Кнудсена, області шляхом розв’язку відповідних рівнянь, наведених в § 9.1. Продовжуючи розв’язок всередину шару Кнудсена (пунктирна лінія на рис.9.4, дотична до розподілу швидкості у точці А на границі) можна визначити деякі фіктивні значення швидкості (і температури) біля стінки. У загальному випадку отримані таким чином швидкість і температура wx(x, 0) і Т(х, 0) не дорівнюють не істинній швидкості і температурі газу біля стінки (на фазовій границі) wxк і Тк (х, 0), не швидкості і температурі стінки. Різниця між фіктивною швидкістю і швидкістю стінки називають швидкістю ковзання, а відповідну різницю температур – температурним стрибком.
Приймаючи фіктивні швидкість і температуру в якості граничних умов, отримуємо рішення, яке співпадає поза шаром Кнудсена з дійсним. Оскільки при розгляді течії при малих числах Кнудсена зазвичай не цікавляться деталями течії у кнудсівському шарі, то швидкість ковзання і температурний стрибок представляють собою необхідну інформацію для розрахунку течії з точки зору механіки суцільного середовища. Але для знаходження стрибків необхідно розв’язувати рівняння Больцмана всередині шару Кнудсена і зшивати це рішення для зовнішньої області по відношенню до кнудсівського шару.
Не зупиняючись на методах розв’язку рівняння Больцмана чи його модифікацій для кнудсівського шару, зауважимо тільки, що зараз вирішення таких задач, пов’язаних з нерівно важністю розглядуваного процесу із-за наявності фазової поверхні, можна отримати тільки з певним наближенням в межах використовуваної розрахункової моделі. Так, у сучасних роботах приймається, що відбиті стінкою молекули мають дифузійний характер з розподілу за швидкостями. При цьому розглядаються тільки стаціонарні (у кращому випадку квазістаціонарні) процеси.
Математичні труднощі і недостатня повнота певних фізичних уявлень не дають можливості вважати, що процес вирішення кінетичних рівнянь для кнудсівського шару і ув’язка цих рішень з рішеннями для зовнішньої області (відносно шару Кнудсена) знаходяться на стадії закінченості. Цю обставину необхідно враховувати при отриманні кінцевих результатів. Але навіть існуючі дані несуть цінну інформацію.
Так для кнудсівського шару, вважаючи, що нормальна макроскопічна швидкість wy набагато більша нормальної складової швидкості в зовнішній області (в пограничному шарі), але менша за с, де с ~ (kT/m)0,5 – характерна швидкість теплового руху молекул (k стала Больцмана, т – маса молекули). Число Маха повздовжнього руху порядку одиниці.
Внаслідок рішення модельного рівняння Крука отримані наступні вирази для облікової густини потоку молекул і стрибка температури у випадку конденсації:
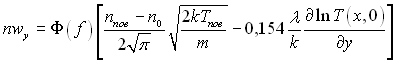 (9.62)
(9.62)
і
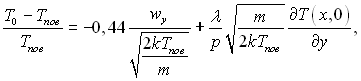 (9.63)
(9.63)
де п – облікова концентрація (густина) молекул; λ – коефіцієнт теплопровідності; р – тиск; індекси 0 і “пов” відповідають параметрам на зовнішній і внутрішній границях кнудсівського шару. Функція коефіцієнта конденсації визначається рівнянням:
![]() (9.64)
(9.64)
У разі великих поперечних витрат, коли задача нелінійна, показано, що гідродинамічні величини змінюються в тонкому кнудсівському шарі на свій порядок. При цьому пограничний шар Прандтля “зникає”, так що зовнішня нев’язка течія відокремлюється від поверхні тіла тільки тонким шаром Кнудсена (під зовнішнім розуміємо течію, зовнішню по відношенню до шару Кнудсена, а не потік, що набігає на тіло ). При цьому класична формула Герца-Кнудсена може давати похибку в два і більше рази. Стрибки швидкості, густини і температури у цьому випадку можуть бути довільними. Для стрибка макроскопічної швидкості пари отримано рівняння
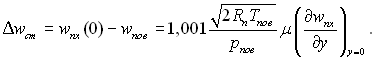 (9.65)
(9.65)
Як слідує з рівняння (9.65), величина Δwст. збільшується зі зменшенням тиску. Специфіка процесу фазового перетворення неявно проявляється через величину (дwnx/дy)y=0, яка залежить від поперечного потоку речовини j.
Для деяких інженерних задач конденсації пари і її суміші з неконденсованим газом термічний опір буває несуттєвим у порівнянні з дифузійним термічним опором, який ураховує послаблення переносу пари до поверхні конденсації. Ця обставина дозволяє нехтувати між фазним опором.
9.3. Безрозмірні змінні величини
Запишемо математичну формулу задачі про теплообмін при плівковій ламінарній конденсації рухомої насиченої пари на зовнішній поверхні вертикальної круглої труби. Швидкість набігання потоку пари спрямована вздовж осі труби і рівна w0. Фізичні властивості пари і конденсату приймаємо незмінними. Внутрішні джерела теплоти відсутні, теплотою тертя нехтуємо. Температура поверхні труби усталена і рівна Тс. На поверхні розриву пара – конденсат відсутнє ковзання і немає стрибка температури.
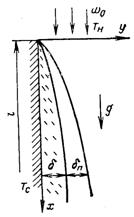
Рис.9.5. До постановки крайової задачі про омивання поверхні двофазним потоком
Шар конденсату δ тонкий у порівнянні з довжиною труби ℓ і її радіусом R, що дозволяє використати наближення плоского пограничного шару (рис.9.5). Записуючи математичне формулювання, температуру будемо відраховувати від температури поверхні труби, тобто будемо вважати, що температура θс = Т – Тс, дорівнює нулю.
У наслідок сказаного, розглядувана спряжена задача може бути сформульована наступним чином.
Шар конденсату. Рівняння енергії:
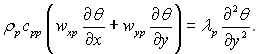
Рівняння руху:
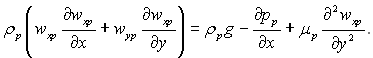
Рівняння нерозривності потоку:
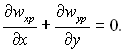
Паровий пограничний шар. Рівняння руху:
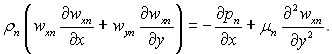
Рівняння нерозривності потоку:
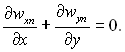
Граничні умови. При у = = ∞ wxn = w0; wyn = 0; θ = Tн – Т0;
при у = 0 wxр = wур = 0; θ = 0.
Умови спряження. Рівняння нерозривності потоку (збереження маси):
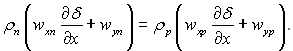
Рівняння кількості руху
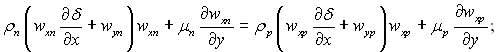
![]()
Рівняння енергії:
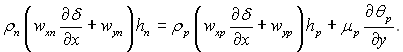
Крім того, при у = δ:
![]()
Для приведення математичного формулювання задачі до безрозмірного запису за масштаби вибираємо довжину труби ℓ, швидкість і температуру набігаю чого потоку w0 і θн. Тоді безрозмірні координати Х і Y, складові швидкості Wx і Wy, температура рідини Θ і товщина плівки Δ будуть зв’язані з розмірними величинами співвідношеннями:
![]()
Використовуючи ці значення, наведене вище математичне формулювання задачі можна записати у безрозмірному вигляді.
Шар конденсату. Рівняння енергії:
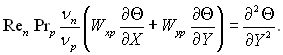 (9.66)
(9.66)
Рівняння руху:
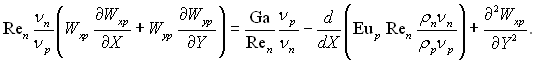 (9.67)
(9.67)
Рівняння нерозривності потоку:
![]() (9.68)
(9.68)
Паровий пограничний шар. Рівняння руху:
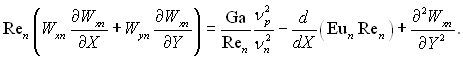 (9.69)
(9.69)
Рівняння нерозривності потоку:
![]() (9.70)
(9.70)
Граничні умови.
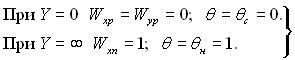 (9.71)
(9.71)
Умови спряження. (Y = Δ). Рівняння нерозривності потоку:
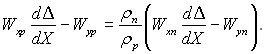 (9.72)
(9.72)
Рівняння кількості руху
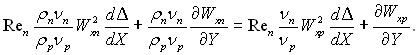 (9.73)
(9.73)
![]() (9.74)
(9.74)
Рівняння енергії:
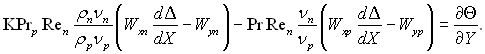 (9.75)
(9.75)
Умови відсутності стрибків швидкості і температури:
![]() (9.76)
(9.76)
У співвідношеннях (9.66)...(9.76) позначено: Ren = w0ℓ/νn – число Рейнольдса пари; Prp = νp/ap – число Прандтля рідини (конденсату); К= r/cppθн – число фазового переходу; Ga = gℓ3/ν2p – число Галілея; Wew = σпр/ρпw20ℓ – число Вебера, є мірою відношення сили поверхневого натягу до інерційної сили. Відома також модифікація Вебера Wew = σпр/ρрgℓ2 – міра відношення поверхневої сили до сили тяжіння.
Згідно математичного формулювання, представленого у вигляді рівнянь (9.66)...(9.76), температурне поле у плівці залежить від наступних величин:
Θ = f1(X, Y, Ren, Ga, K, Prp, νn/νp, ρn/ρp, Wew, R/ℓ). (9.77)
Комбінуючи величини, які стоять під знаком функції, можна ввести замість Wew число Wew = σпр/ρрgℓ2:
Θ = f2(X, Y, Ren, Ga, K, Prp, νn/νp, ρn/ρp, We, R/ℓ). (9.78)
Коефіцієнт тепловіддачі від конденсату до поверхні стінки можна розраховувати за формулою
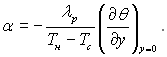 (9.79)
(9.79)
Приведемо отримане рівняння до безрозмірного вигляду, матимемо
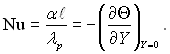 (9.80)
(9.80)
Згідно рівнянню (9.80) число Нуссельта Nu має зміст безрозмірної похідної від температури по нормалі до стінки, взятої на її поверхні. З рівнянь (9.78) і (9.80) виходить, що
Nu = f3(Xc, Yc, Ren, Ga, K, Prp, νn/νp, ρn/ρp, We, R/ℓ). (9.81)
У цьому рівнянні незалежні змінні Xc і Yc характеризують положення точок на поверхні стінки.
Співвідношення (9.77), (9.78) і (9.81) дають перелік величин Ren, Ga, K, Prp, νn/νp, ρn/ρp, We, які задаються умовою задачі. Ці величини часто використовуються для характеристики течії і теплообміну при плівковій конденсації пари. У залежності від постановки задачі кількість і вид змінних, які знаходяться під знаком функції, може змінюватися. Список безрозмірних змінних завжди залежить від постановки задачі. В межах одного і того ж формулювання вид безрозмірних змінних (їх зміст) може змінюватися, якщо використовувати можливість комбінування змінних. Наприклад, комбінуванням відповідних змінних в (9.81) чи (9.78) замість Ren можна ввести (ρn/ρp)Fr, де число Фруда Fr = w20/gℓ. Загальна кількість безрозмірних змінних при цьому повинна залишатися незмінною.
У межах одного і того ж формулювання число змінних може бути формально скорочене, якщо розв’язок задачі показує, що залежна змінна однаково залежить від незалежних змінних чи постійних, які задаються умовою задачі. Наприклад, рішення деяких задач про теплообмін при конденсації нерухомої пари приводить до рівняння виду
Nu = c(GaKPrp)n.
У цьому випадку добуток GaKPrp можна прийняти за одну змінну.