Розділ 10. ТЕПЛООБМІН ПРИ ПЛІВКОВІЙ КОНДЕНСАЦІЇ НЕРУХОМОЇ ЧИСТОЇ ПАРИ
10.1. Ламінарна течія плівки
10.1.1. Вертикальна плоска поверхня
Розглянемо класичну задачу про ламінарну плівкову конденсацію однокомпонентної нерухомої пари на вертикальній плоскій пластині, вперше розв’язану В.Нуссельтом.
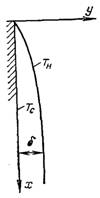
Рис.10.1. До постановки задачі про ламінарну плівкову конденсацію на вертикальній поверхні
На вертикальній стінці, температура поверхні якої у всіх точках однакова і рівна Тс, конденсується суха насичена пара (рис.10.1). Плівка, товщиною δ, стікає ламінарно. Задача стаціонарна.
Приймемо наступні допущення:
1) сили інерції, які виникають у плівці конденсату, незначні в порівнянні з силами в’язкості і силами тяжіння;
2) конвективний перенос теплоти у плівці, а також теплопровідність вздовж неї несуттєві в порівнянні з теплопровідністю поперек плівки;
3) тертя на границі розділу парової і рідкої фаз відсутнє;
4) температура зовнішньої поверхні плівки конденсату постійна і рівна температурі насичення Тн при заданому тиску пари;
5) фізичні параметри конденсату не залежать від температури;
6) сили поверхневого натягу на вільній поверхні плівки не впливають на характер її течії;
7) густина пари мала в порівнянні з густиною конденсату.
Прийняті допущення дозволяють суттєво спростити математичне формулювання задачі. Рівняння енергії (9.8) і рівняння руху (9.15) записуються відповідно в наступному виді:
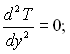(10.1)
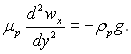(10.2)
Граничні умови:
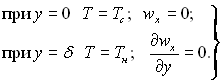(10.3)
Розглянемо виконані спрощення диференціальних рівнянь енергії і руху. Ліва частина рівняння енергії (9.8) дорівнює нулю, тому що процес усталений і конвективний перенос теплоти не враховується. Будуть дорівнювати нулю і похідні д2Т/дх2 і д2Т/дz2, тому що перенос теплоти теплопровідністю вздовж плівки дуже малий.
Плівка рухається у напрямку осі х. Ліва частина рівняння руху в проекції на ось х дорівнює нулю, тому що задача стаціонарна і інерційні сили вважаються дуже малими. Похідна др/дх = 0 тому, що зміна тиску вздовж осі х визначається тільки зміною гідростатичного тиску пари, густина якої мала в порівнянні з густиною конденсату, а висота стінки невелика. Якщо густину пари ρп можна порівнювати з густиною рідини ρр, у рівнянні руху (10.2) замість ρрg слід підставляти член g(ρр – ρп). Усі похідні по z вважаються рівними нулю у зв'язку з тим, що задача плоска.
Граничні умови дwx(δ)/ду = 0 відповідає допущенню про те, що на вільній поверхні (у = δ) плівки тертя відсутнє.
Інтегрування рівняння енергії при назначених граничних умовах дає:
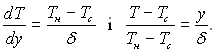(10.4)
Коефіцієнт тепловіддачі:
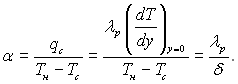(10.5)
Інтегруючи двічі рівняння руху (10.2) з використанням граничних умов (10.3) отримаємо параболічний закон розподілу швидкості по товщині плівки:
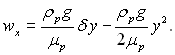(10.6)
Середня швидкість в перерізі х становить:
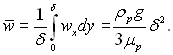(10.7)
У рівняння (10.4)...(10.7) входить змінна товщина плівки δ = δ(х). Змінність δ обумовлена безперервним вздовж осі х надходженням конденсату до плівки. Якщо вважати, що теплота, яка віддається стінці, є теплотою фазового переходу, тобто якщо знехтувати теплотою переохолодження конденсату відносно температури насичення, приріст витрат плівки на елементі поверхні dx·1 можна виразити наступним чином:
де qc/r = jгр – густина потоку маси, кг/(м2·с).
З іншого боку, зміну витрат конденсату можна описати виразом
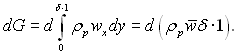
З двох останніх рівнянь виходить, що
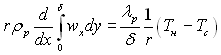(10.8)
чи
Підставляючи, наприклад, в останнє рівняння значення середньої швидкості з (10.7), отримаємо наступне диференціальне рівняння:
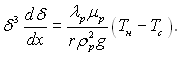
Після інтегрування отримаємо:
де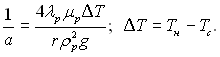 
Сталу інтегрування С визначаємо з початкових умов, згідно з якими при х = 0 маємо δ = 0. Звідки С = 0, і тоді
(10.9)
чи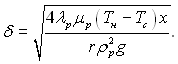 
(10.10)
Підставляючи значення δ у вираз (10.5), отримаємо наступне рівняння для місцевого (локального) коефіцієнта тепловіддачі:
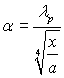(10.11)
чи
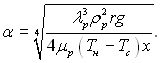(10.12)
Середній коефіцієнт тепловіддачі на стінці висотою Н визначається з рівняння
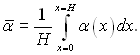
Після інтегрування знаходимо, що
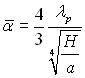(10.13)
чи
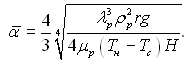(10.14)
З рівнянь (10.11) і (10.13) виходить, що
(10.15)
де αх=Н – місцевий коефіцієнт тепловіддачі в перерізі, де х = Н.
У випадку конденсації на вертикальних трубах малого діаметра на тепловіддачу може впливати кривизна утворюваної плівки конденсату. Якщо пара конденсується на зовнішній поверхні труби, поверхня плівки з боку пари більша, ніж поверхня на межі зі стінкою. Ця обставина сприяє збільшенню коефіцієнта тепловіддачі при фіксованій температурі стінки. Зворотна картина повинна мати місце при конденсації на ввігнутій внутрішній поверхні.
Г.В’юнш розв’язав задачу за умов, які відповідають прийнятим Нуссельтом для вертикальної плоскої поверхні. Наведемо основні результати цього рішення.
Розподіл повздовжньої швидкості по товщині плівки описується рівнянням
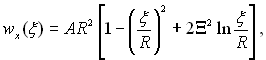(10.16)
де ξ – поточний радіус; Ξ = Δ/R; А = ρрg/4μp; Δ = R ± δ, знак “мінус” відповідає конденсації на ввігнутій поверхні, “плюс” – на зовнішній поверхні труби; R – відповідно зовнішній чи внутрішній радіус труби.
З рівняння (10.16) виходить, що середня за товщиною плівки швидкість може описуватися співвідношенням:
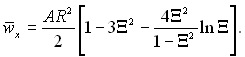(10.17)
Зміна температури за товщиною плівки описується рівнянням
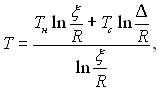
якому відповідає вираз
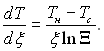
Тоді густина теплового потоку буде визначатися рівнянням
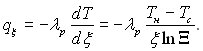(10.18)
Цей результат справедливий і для внутрішньої, і для зовнішньої задачі, якщо врахувати, що в останньому випадку знак біля qξ повинен бути зміненим на зворотний.
З рівняння (10.18) виходить, що коефіцієнт тепловіддачі можна визначати з формули:
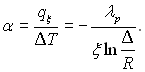(10.19)
Вважаючи, що плівці передається теплота фазового переходу, яка транзитом проходить крізь стінку, і витрати конденсату визначаються тільки процесом конденсації, з рівняння балансу теплоти і раніше отриманих рівнянь можна отримати формулу, яка дозволяє визначати положення поверхні плівки і її товщину:
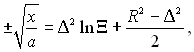
де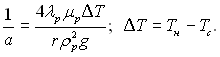
Для обох розглядуваних випадків інтерес викликають тільки додатні корні. Визначаючи середнє значення коефіцієнта тепловіддачі як середньо інтегральний згідно рівнянню
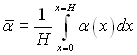
і використовуючи формули (10.19) і (10.20), отримаємо, що
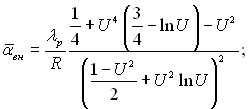(10.21)
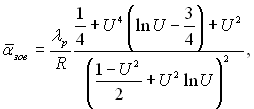(10.22)
де α|вн, α|зов – середні коефіцієнти тепловіддачі відповідно з внутрішньої і зовнішньої сторони циліндричної стінки; U = ΔH/R = R ± δH/R; δH – товщина плівки при х = Н; Н – висота (довжина) труби. Координата х відраховується від верхньої кромки труби.
Вплив кривизни поверхні на тепловіддачу можна показати за допомогою поправок
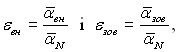(10.23)
які представляють собою відносний коефіцієнт тепловіддачі відповідно на внутрішній і зовнішній поверхнях. У цьому рівнянні 
– середній коефіцієнт тепловіддачі, який визначається згідно формули Нуссельта для плоскої поверхні:
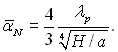(10.24)
З рівнянь (10.21)...(10.24) виходить, що
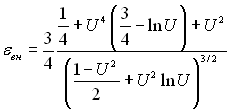(10.25)
і
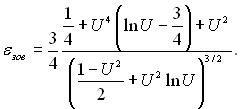(10.26)
Аналіз виразів (10.25) і (10.26) показує, що εвн ≤ 1 і εзов ≥ 1. Зникаючій малій товщині плівки в нижній частині труби відповідає значення U = 1 ± δH/R, рівне одиниці. Якщо δH/R → 0, то кривизна не повинна впливати на теплообмін і, як наслідок, U = 1 відповідає εвн = 1 і εзов = 1.
Розрахунки за формулами (10.25) і (10.26) показують, що в інтервалі 0,5<U<2 поправки εвн і εзов з хорошим наближенням можна описати виразом
У цьому разі
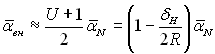(10.27)
і
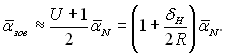(10.28)
Таким чином, середній коефіцієнт тепловіддачі зовні труби збільшується зі зменшенням її діаметра 2R, а середній коефіцієнт тепловіддачі при цьому зменшується. Значення δн можна визначити за формулою (10.20).
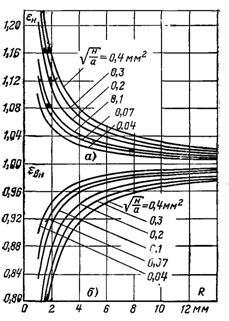
Рис.10.2. Вплив радіусу вертикальної труби на коефіцієнти тепловіддачі: а) із зовнішньої сторони; б) з внутрішньої сторони
На рис.10.2 наведена залежність поправок εвн і εзов від радіуса труби при значеннях (Н/а)0,5, що змінюються від 0,04 до 0,4 мм2. З рисунка видно, що у розглядуваних випадках поправки суттєві при радіусах труб, менших ~10 мм.
10.1.3. Змінна температура поверхні стінки
Отримані раніше рішення передбачають найпростіші теплові граничні умови на поверхні холодної стінки, приймалося, що Тс = const. На практиці найчастіше приходиться мати справу з умовами, коли Тс змінюється по поверхні стінки.
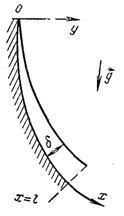
Рис.10.3. До постановки задачі про ламінарну плівкову конденсацію зі змінною температурою поверхні стінки
В якості поверхні конденсації будемо розглядати деякий криволінійний контур (рис.10.3). Його орієнтація відносно вектора прискорення вільного падіння g довільна. Вважаючи, що товщина плівки конденсату менше радіуса кривизни поверхні. Задача плоска. Використаємо криволінійні координати: х – вздовж поверхні конденсації; у – по нормалі до заданої точки поверхні. Загальна довжина поверхні конденсації х = ℓ.
Розподіл температури Тс вздовж поверхні конденсації довільний, але Тс у всіх точках поверхні нижче фіксованої температури насичення Тн. Внаслідок цього температурний напір ΔТ(Х) = Тн – Тс(Х), де Х = х/ℓ, хоч і змінюється вздовж Х, але має додатне значення.
Д.О.Лабунцов розв’язав сформульовану задачу, залишаючи в силі всі інші допущення теорії Нуссельта. Вихідні рівняння енергії і руху мають вид:
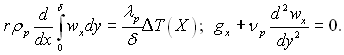
Розподіл температури ΔТ(Х) можна представити аналітично за допомогою функції розподілу неізотермічності ψ(Х) у виді
де 
– середній температурний напір чи середня надлишкова температура поверхні. На підставі такого уявлення функції неізотермічності, очевидне нормування:
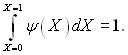
Форма поверхні конденсації і її орієнтація відносно вектора прискорення вільного падіння можуть задаватися аналітично у виді функції
яка вважається відомою. Тоді замість величини gx у рівняння руху можна ввести gf(X). У загальному випадку замість g можна ввести ефективне прискорення ge = g(ρр – ρп)/ρр.
Інтегрування рівняння руху дає звичайний параболічний розподіл швидкості по товщині плівки. Після підстановки розподілу в рівняння енергії і інтегрування по товщині плівки отримуємо:
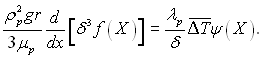
Введемо позначення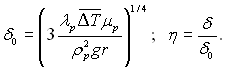 
Тоді останнє рівняння можна записати в наступному вигляді:
Помноживши обидві частини рівняння на f1/3 і після інтегрування по Х в межах від 0 до Х, отримаємо:
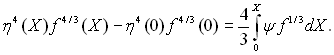
Другий доданок лівої частини цього співвідношення необхідно випустити. Для контуру з гострою верхньою кромкою, коли f(0) ≠ 0, величина η(0) = 0. Для контуру з плавним обрисом верхньої твірної (типу горизонтального циліндра) f(0) = 0. З урахуванням цього, можна записати рівняння для товщини стікаючої плівки:
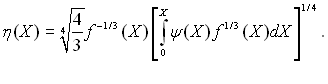(10.29)
З рівнянь (10.1) і (10.29) можна отримати наступне співвідношення для локального значення
α(Х) =
qc(X)/ΔT(X) і середнього 
коефіцієнтів тепловіддачі:
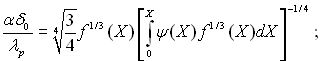(10.30)
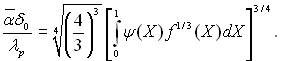(10.31)
Рівняння (10.31) дозволяє зробити наступні загальні висновки про вплив неізотермічності поверхні стінки на середній коефіцієнт тепловіддачі. Одна і та ж неізотермічність проявляється по-різному в залежності від кривизни поверхні. На прямолінійних поверхнях (пластинах) середній коефіцієнт тепловіддачі інваріантний відносно нерівномірності поля температур поверхні стінки. Дійсно, на пластині f(X) = const. Тому у виразі (10.31) права частина згідно умови нормування функції ψ((Х) не залежить від виду цієї функції.
Для криволінійних контурів, в яких f(X) ≠ const, нерівномірність температури поверхні впливає на середню тепловіддачу.
Запишемо вираз для середнього коефіцієнта тепловіддачі за умови, що густина теплового потоку на поверхні стінки qc постійна. З рівняння (10.29) функцію неізотермічності можна виразити наступним чином:
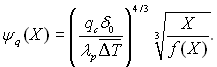(10.32)
Використовуючи раніше записану умову нормування, отримаємо:
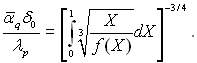(10.33)
Цей вираз визначає середній коефіцієнт тепловіддачі на криволінійних контурах для окремого випадку неізотермічності типу qc = const.
