10.1.4. Горизонтальна труба

Ця задача викликає інтерес для інженерної практики. Для горизонтальної труби

де πХ – кут, який відраховується від верхньої твірної труби.

Використовуючи ці величини, з рівняння (10.31) для Т_с = const можна отримати:

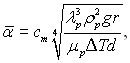(10.34)

де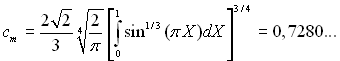

При q_c = const

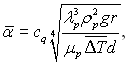(10.35)

де с_q = 0,6928... ≈ 0,69

Порівняння формул (10.34) і (10.35) показує, що за інших рівних умов середній коефіцієнт тепловіддачі горизонтальної труби при Т_с = const більший, ніж при q_c = const. Різниця при цьому невелика і становить біля 5%. Цей результат справедливий для прийнятого закону осереднення коефіцієнта тепловіддачі

Якщо осереднення виконати по закону

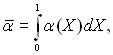
то середні коефіцієнти тепловіддачі можуть бути різними. При Т_с = const немає різниці в значеннях α, отриманих методами. Для неізотермічної поверхні останній закон осереднення не представляє практичного інтересу, тому що для визначення кількості переданої теплоти необхідно спеціально підбирати температурний напір.

10.1.5. Вплив змінності фізичних властивостей конденсату

У практичних розрахунках урахування залежності фізичних параметрів конденсату від температури часто виконують, вибираючи у формулі Нуссельта за визначальну середню температуру плівки, рівну середній арифметичній температурі між температурами насичення Т_н і стінки Т_с. При довільному законі зміни фізичних властивостей конденсату від температури отримано рішення для тепловіддачі при ламінарній плівковій конденсації нерухомої насиченої пари на плоских вертикальних поверхнях у виді

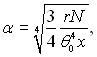(10.36)

де 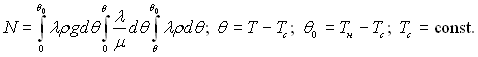(10.37)

Д.О.Лабунцов в одному з варіантів розрахунку прийняв наступну залежність фізичних властивостей конденсату від температури:

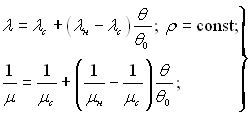(10.38)

де індексами “н” і “с” позначені відповідні фізичні параметри вибрані по температурі насичення і температурі стінки.

Вираз для коефіцієнта тепловіддачі, розрахованого за рівнянням (10.36) з використанням залежностей (10.38), має вигляд:

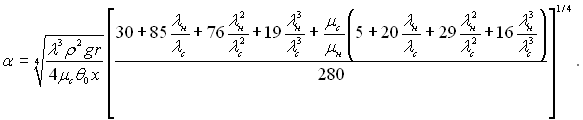(10.39)

Вираз для коефіцієнта тепловіддачі за формулою Нуссельта при визначальній температурі 0,5(Т_н – Т_с) і використанні умов (10.38) буде:

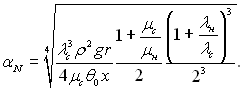(10.40)

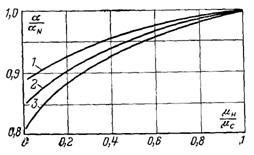
Рис.10.4.Зміна коефіцієнта тепловіддачі в залежності від зміни λ_р і μ_р з температурою:α_N  – розрахунок за (10.14) при визначальній температурі 0,5(Т_н + Т_с); 1 – λ_н/λ_с = 2; 2 – λ_н/λ_с = 1; 3 –λ_н/λ_с = 0,5

Порівняння розрахунків за рівняннями (10.39) і (10.40) наведено на рис.10.4 у вигляді залежності

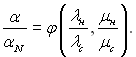
З рисунка видно, що при віднесенні фізичних параметрів до середньоарифметичної температури плівки конденсату результати виходять завищеними. При значній зміні в’язкості по перерізу плівки похибка може досягати 15...20%.

Д.О.Лабунцов запропонував побудувати розрахункове рівняння наступним чином:

(10.41)

де всі фізичні параметри, які входять у параметр α_н віднесені до температури насичення Т_н:

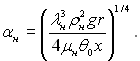
Величина ε_t =ψ(λ_н/λ_с, μ_н/μ_с) не що інше, як поправка на вплив залежності фізичних властивостей конденсату від температури. Температура насиченої пари на відміну від температури поверхні стінки зазвичай відома при інженерних розрахунках.

Перерахунок рівняння (10.39) до виразу (10.41) приводить до наступного значення поправки:

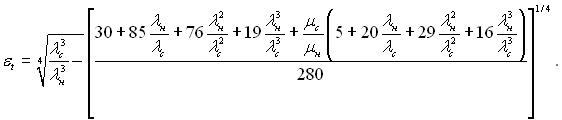(10.42)

У досить широкому діапазоні зміни фізичних параметрів 0,1≤ μ_н/μ_с≤ 1,0; 0,5 ≤ λ_н/λ_с ≤ 2,0 формула (10.42) апроксимується наступною простою залежністю:

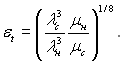(10.43)

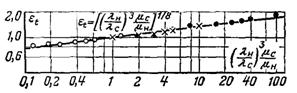
Рис.10.5. Порівняння розрахунку за апроксимаційною залежністю (10.43) – суцільна лінія, з розрахунком по рівнянню (10.42) – точки: ● – λ_н/λ_с = 2; × – λ_н/λ_с = 1; ○ –λ_н/λ_с = 0,5  

Порівняння розрахунків за формулами (10.42) і (10.43) наведено на рис.10.5

При усталеній температурі стінки залежність (10.43) буде справедлива також для розрахунку середнього коефіцієнта тепловіддачі. Цю формулу можна застосовувати також при розрахунку середнього коефіцієнта тепловіддачі горизонтальної труби. Змінюються тільки вирази і значення для величини α_н.

У розглядуваному рішенні густина конденсату вважається незмінною величиною. Виконані розрахунки, коли вважалося, що густина є функцією температури, а інші фізичні параметри усталені, показали, що вплив вільної конвекції на течію і теплообмін рідких плівок при умовах, які зустрічаються на практиці, незначний. Вплив вільної конвекції збільшується з підвищенням тиску і стає суттєвим в термодинамічній біля критичної області станів.

10.1.6. Вплив конвективного теплопереносу і інерційних сил

Теплові потоки через поверхню плівки пара – рідина і через поверхню стінки, взагалі різні. Крім теплоти фазового переходу, яка транзитом проходить через плівку, остання віддає стінці частину своєї фізичної теплоти, оскільки температура по товщині плівки змінюється від Т_пов = Т_н до Т_с. У середньому конденсат охолоджується до температури Т, яку, вважаючи фізичні параметри усталеними, можна визначити з рівняння

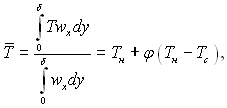(10.44)

де 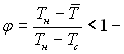відносне переохолодження конденсату.

Загальна кількість теплоти, яка передається стінкою і є сумою теплоти фазового переходу і теплоти переохолодження відносно температури фазового переходу, може бути виражена рівнянням

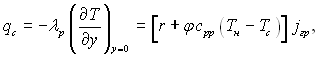(10.45)

де j_гр – густина потоку маси на поверхні плівки пара – рідина, обумовлена конденсацією, кг/(м²·с). Якщо знехтувати теплотою переохолодження, як це зроблено в теорії Нуссельта, то другий член, який стоїть в квадратних дужках, повинен випасти.

З останнього рівняння слідує, що

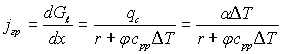(10.46)

чи для осереднених вздовж х величин

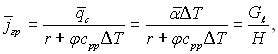(10.47)

де G_ℓ – витрати конденсату через даний поперечний переріз плівки шириною в одиницю, кг/(м·с); Н – довжина ділянки осереднення від х = 0 до х = Н.

Вираз для G_ℓ можна записати так:

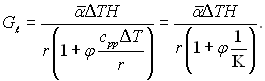(10.48)

Величину φ можна представити наступним чином:

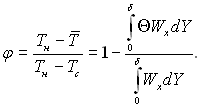(10.49)

У цьому рівнянні

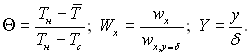
Якщо вважати, що Θ = Y (лінійний розподіл), а W_x = 2Y – Y² (параболічний розподіл), то після інтегрування отримаємо φ =3/8. Тоді

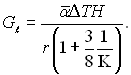(10.50)

Для звичайних умов конденсації числа К достатньо великі, що дозволяє у більшості випадків нехтувати членом . Наприклад, якщо К = 5, то =0,075.

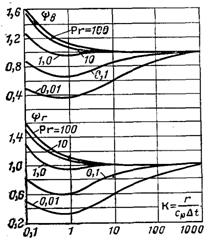
Рис.10.6. Вплив конвективного переносу, сил інерції у плівці і тертя між плівкою і нерухомою парою на тепловіддачу ламінарно стікаючої плівки конденсату

На рис.10.6 наведені результати теоретичного аналізу плівкової конденсації при ламінарній течії на вертикальній поверхні і на горизонтальній трубі. Тут ψ_в = α_в/α_Nв і ψ_г = α_г/α_N г, де α_в і α_г – коефіцієнти тепловіддачі при конденсації на вертикальній стінці і горизонтальній трубі з урахуванням інерційних сил, конвективного переносу теплоти і сил тертя між поверхнею плівки і нерухомою парою; α_Nв і α_Nг– ті ж коефіцієнти розраховані за формулами Нуссельта для вертикальної плоскої поверхні (10.13) і горизонтальної труби (10.34).

З рис.10.6 виходить, що при К = r/c_ppΔT > 5 і 1≤ Pr ≤ 100  досягається достатньо добре спів падіння більш повних рішень з рішенням Нуссельта. Різниця в коефіцієнтах тепловіддачі становить тільки декілька відсотків і може не враховуватися в інженерних розрахунках.

При великих температурних напорах чи в області недалекої від критичної, де r/c_pp стрімко зменшується, коефіцієнт тепловіддачі значно зростає у порівнянні з α  розрахованими за рівнянням Нуссельта.

10.1.7. Вплив хвильового руху плівки

Ламінарна течія рідкої плівки може супроводжуватися хвильовим рухом. Частинки рідини, які знаходяться на поверхні плівки, під дією випадкових подразнень можуть зміщуватися, що призводить до деформації поверхні і її відхилення від рівноважного стану. При цьому виникають сили, які намагаються повернути поверхню рідини до рівноважної форми. За інерцією частинки рідини будуть проходити положення рівноваги, знову відчувати дію сил поновлення структури і т. д. У наслідок цього на поверхні плівки, яка підпадає під дію сил подразнення, будуть виникати хвилі. Виникнення і підтримування хвиль на поверхні плівки, яка тече у практично нерухомому газі (парі), залежить від сил тяжіння, в’язкості і поверхневого натягу. В загальному випадку необхідно враховувати також інерційні сили.

Спостереження показують, що при малих значеннях числа Рейнольдса, має місце рух без утворення хвиль. Амплітуда хвиль приблизно лінійно збільшується з ростом Re.

Подальше збільшення Re призводить до руйнування синусоїдального характеру хвиль. Хвилі мають вигляд напливу з круглим фронтом і пологою тильною стороною. Хвильові рухи, які виникають в різний час і в різних місцях від випадкових збудників, накладаються одна на іншу і ведуть до складної тримірної картини процесу. Це призводить до того, що виникають значні труднощі в теоретичному дослідженні такого складного хвильового руху. При аналізі процесу приходиться обмежуватися окремими спрощеними моделями.

Досліди з водяною парою і парами гліцерину показали, що при значних температурних напорах і числах Рейнольдса має місце відхилення дослідних даних коефіцієнтів тепловіддачі від розрахованих за формулою Нуссельта. Відхилення тим більше, чим вищий температурний напір чи число Рейнольдса плівки. При Re ≤ 8 дослідні і розрахункові дані практично співпадають.

Питання стійкості ламінарної течії плівки, таким чином, набувають важливого значення для розрахунку теплообміну. При цьому розрізняють конвективну і абсолютну нестійкість. При конвективній нестійкості подразнення, яке раз виникло, збільшується з часом, але воно зноситься вниз потоком. Під абсолютною нестійкістю розуміють таку, яка характеризується збільшенням подразнення в часі у даній точці потоку. При наявності абсолютної нестійкості, строго кажучи, ламінарний рух не може відбуватися.

Досліди показують, що ламінарний рух плівки завжди володіє конвективною нестійкістю відносно подразнень з довжиною хвилі, набагато більшою за товщину плівки. Наявність конвективної нестійкості не говорить про неможливість здійснення ламінарної течії. При малих числах Рейнольдса подразнення, які виникають в плівці зносяться вниз за течією і не приводять до утворення будь якого стійкого режиму. Якщо число Рейнольдса плівки перевищує деяке граничне Re_хв, то утворюється стійкий хвильовий режим. При Re < Re_хв такий режим неможливий.

Дослідно доказано, що плівка не володіє абсолютною нестійкістю. З цього слідує, що при повному позбавленні подразнень, можливий перехід від ламінарного руху плівки до турбулентного, минаючи хвильовий рух. Хвильовий режим зазвичай спостерігається при Re > Re_хв ≈ 5. При періодичному хвильовому русі плівки в’язкої рідини, яка стікає по вертикальній поверхні під дією сил тяжіння

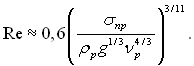(10.51)

Оцінка збільшення коефіцієнта тепловіддачі за рахунок хвильового руху зроблена П.Л.Капицею. Він аналітично розглянув двомірну вільно стікаючу ізотермічну плівку з постійними витратами. Вважаючи, що хвильовий рух має усталений періодичний характер (рис.10.7).

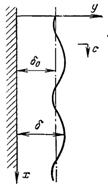
Рис.10.7. Хвильова періодична течія рідкої плівки

Миттєва товщина плівки δ над довільною фіксованою точкою поверхні змінюється в часі τ = t/t₀ (t₀  – період проходження хвилі) по закону

Показано, що амплітуда а в першому наближені стала і рівна 0,46; середня товщина плівки δ₀ = 0,93δ_N, де δ_N  –товщина плівки згідно рішенню Нуссельта при тій же витраті рідини.

З найбільшою швидкістю рухаються частинки рідини, які знаходяться на поверхні плівки. При хвильовому русі ця швидкість завжди менша фазової швидкості с, у зв'язку з цим частинки рідини, що знаходяться на поверхні, будуть послідовно розміщуватися на різних частинах хвильового профілю. Максимальна швидкість частинок має місце на вершині хвилі; у самій тонкій частині шару напрямок поверхневої швидкості змінюється на зворотний.

Хвильовий рух призводить до зміни теплопровідності ламінарно стікаючої плівки. Середню теплопровідність плівки можна визначити наступним чином:

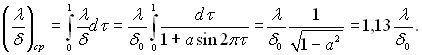
Таким чином, тільки за рахунок хвильової поверхні плівки її теплова провідність збільшується на 13%, а збільшення інтенсивності теплообміну через таку плівку в порівнянні з розрахунком Нуссельта становить:

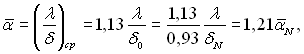
тобто становить 21%. Введена поправка у формулу Нуссельта α|/α| = 1,21 отримана за умов, що рух плівки ізотермічний, а хвильовий характер періодичний. Слід відмітити, що тримірний хвильовий рух настає при витратах (чи числах Re), що перевищують в 4...5 разів витрати, які відповідають виникненню перших хвиль.

Виходячи з уявлення, згідно з яким течія шарів рідини має переважно тримірний, хаотичний характер, і використовуючи результати другого наближення рішення П.Л.Капиці, Д.О.Лабунцов показав, що збільшення теплопровідності рідкої плівки внаслідок хвильової періодичної течії не залишається постійною, а залежить від ReKa^–1/11, де Ка = σ³/gρ³ν⁴_p  – число Капиці, яке враховує співвідношення сил поверхневого натягу, об’ємних сил і сил в’язкості.

Величина Ka^–1/11 для багатьох речовин за звичайних умов конденсації змінюється порівняно слабко. Тому у першому наближенні вважати, що поправка на хвильовий рух залежить тільки від Re, тоді

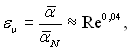(10.52)

де Re = wÑδ/ν_p. При малих числах Re поправка на хвильовий рух ε_υ знаходиться не далеко від одиниці. В міру збільшення Re поправка ε_υ зростає, так при   Re = 400 ε_υ = 1,27.

Згідно спостережень хвильова течія розвивається на протязі ділянки в декілька довжин хвиль. Отже, хвильовий рух плівки, що стікає стінці горизонтальної труби, може виникнути тільки у тому випадку, коли діаметр труби достатньо великий, тому що тільки у цьому випадку буде достатня протяжність поверхні плівки для розвитку хвильової течії. Для довжини хвилі λ_хв в момент виникнення хвильової течії П.Л.Капицею запропонована формула:

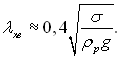
На підставі цього рівняння отриманий оціночний вираз для значення діаметра труби, за якого має місце хвильова течія:

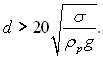
Наприклад, при конденсації водяної пари (Т_н = 373 К) на горизонтальній трубі згідно останнього виразу хвильова течія буде мати місце, якщо d > 50 мм.

10.1.8. Порівняння аналітичних і дослідних даних

Для порівняння дослідних даних по середньому коефіцієнту тепловіддачі вертикальних плоских поверхонь і горизонтальних труб формулу Нуссельта (10.14) зручно представити у вигляді зв'язку між безрозмірними змінними. У традиційній формі запису рівняння (10.14) має вид:

(10.53)

де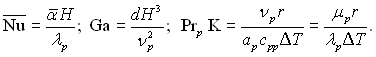

Зручною формою представлення безрозмірної величини у вигляді лінійного масштабу є комплекс введений С.С.Кутателадзе (ν²_р/g)^1/3. Тоді отримаємо:

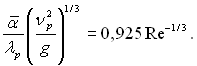(10.54)

Ураховуючи рівняння (10.48), число Рейнольдса Re = w|δ/ν_p = G_ℓ/μ_p, можна виразити через густину теплового потоку:

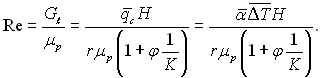(10.55)

Якщо знехтувати теплотою переохолодження конденсату відносно температури насичення (φ/К << 1), то

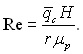(10.55.1)

При φ/К = 3/(8К) і К > 5 похибка, пов’язана з неврахуванням теплоти переохолодження, становить менше 7,5%.

Зауважимо, що число Рейнольдса можна представити в наступному виді:

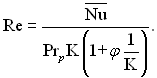
Таким чином, в даному випадку гідродинамічне число подібності одночасно виступає в ролі величини, яка безпосередньо характеризує інтенсивність теплообміну. В подальшому будемо використовувати величину Re при φ/К → 0, тобто Re = q|_cH/(rμ_p).

Якщо прийняти число Re за величину, що визначається, то формулу Нуссельта можна представити в такому виді:

Re = 0,943Z^3/4, (10.56)

де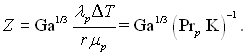

У тому випадку, коли густина рідини і парової фази співрозмірні між собою, у вихідне рівняння руху (10.2) для урахування підйомної сили замість ρ_рg вводиться величина g(ρ_р – ρ_п). Внаслідок цього, залишаючи усі попередні допущення теорії, отримаємо рівняння, в якому замість числа Галілея  Ga = gH³/ν²_p, з’являється число Архімеда

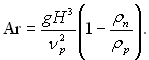
В окремому випадку, величину 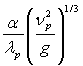необхідно записати так:

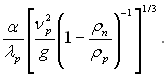
Як було показано раніше, що при Pr > 1 і К > 5 можна запропонувати наступну розрахункову формулу для середнього коефіцієнта тепловіддачі на вертикальній плоскій поверхні:

(10.57)

де перший співмножник правої середній коефіцієнт тепловіддачі, який визначається за формулою Нуссельта (10.14); другий і третій співмножники – поправки, які враховують відповідно вплив змінних фізичних параметрів і хвильового руху плівки. Раніше було показано, що для вертикальної стінки середній коефіцієнт тепловіддачі не залежить від характеру зміни температури поверхні стінки. Коефіцієнт можна розрахувати за формулою (10.14) і по її модифікаціям (10.53), (10.54), (10.56).

Формулу (10.57) з урахуванням залежностей (10.56) і (10.52), вважаючи, що , можна представити у наступному виді:

(10.58)

Індекс “н” показує, що фізичні параметри конденсату, які входять в Re і Z, вибираються по температурі насичення. Поправка ε_υ входить в рівняння (10.58) у неявному виді.

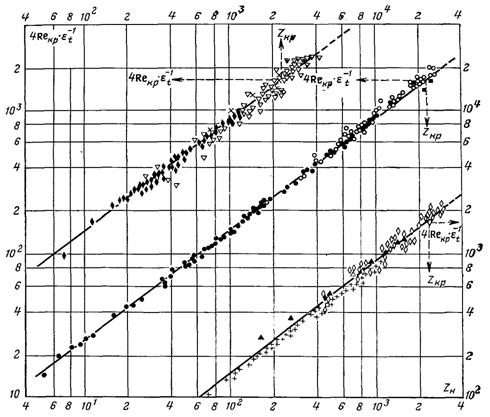
Рис.10.8. Тепловіддача при плівковій конденсації нерухомої пари на вертикальній поверхні при ламінарному режимі руху плівки: ў – вода, Геббард;l – аміак, Городянська; Ё – етанол, Беккер; n – рідке повітря, Головінський; r – вода, Саліков;p – ацетон, Беккер; s – вода, Стробе; И – вода, Буров; Н – бензол, Беккер; Ї – вода, Мейсенбург; ї – вода, Кутателадзе

Формула (10.58) порівнювалася з великою кількістю дослідних даних, отриманих в дослідах з конденсацією пари різних рідин на вертикальних трубах. Результати порівняння при Re < 400 наведені на рис.10.8. За критичне число Рейнольдса, яке відповідає переходу ламінарної течії у турбулентну, прийнята величина Re_кр = 400. Цьому значенню, згідно формули (10.58), відповідає Z_кр ≈ 2300 (при цій оцінці прийнято, що ε_t = 1).

Порівняння, наведене на рис.10.8, показує, що формула (10.58) в основному задовільно описує дослідні дані.

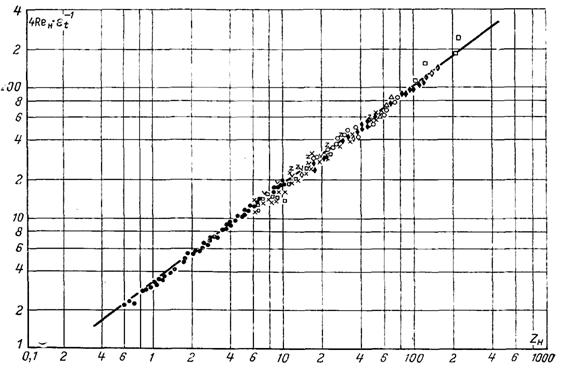
Рис.10.9. Тепловіддача горизонтальних труб при плівковій конденсації

На рис.3.9 в координатах Re_нε_tt^–1 = f(Z_н) наведені дослідні дані при конденсації пари різних рідин на зовнішній поверхні горизонтальних труб. Апроксимаційна лінія відповідає рівнянню:

(10.59)

За визначальний розмір, який входить в числа Re_н і Z_н, вибрана половина довжини кола πd/2, де d – діаметр труби.

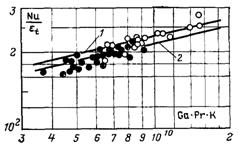
Рис.10.10. Тепловіддача горизонтальних труб при плівковій конденсації водяної пари: 1 – Т₀ = const; 2 – q₀ = const;  – Ісаченко-Богородський;  – Ісаченко-Глушков

На рис.10.10 наведені дослідні дані при конденсації практично нерухомої водяної пари на горизонтальних трубках діаметром біля 12 мм. Трубки з середини охолоджувалися водою. У залежності від режиму теплові граничні умови були близькими до умови Т_с = const, чи до умови q₀ = const. Дослідні дані непогано погоджуються з результатом розрахунку за формулами (10.34)чи (10.35) з урахуванням поправки ε_t. Тут у числа Нуссельта і Галілея як визначальний розмір введений зовнішній діаметр труб.