




10.2. “урбулентна теч≥€ конденсату
” турбулентному потоц≥ густина теплового потоку ≥ дотичне напруженн€ в певному перер≥з≥, €кий паралельний тверд≥й ст≥нц≥, можуть описуватис€ р≥вн€нн€ми:
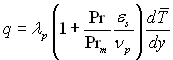 (10.60)
(10.60)
≥
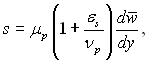 (10.61)
(10.61)
де εs Ц к≥нематичний коеф≥ц≥Їнт турбулентного переносу к≥лькост≥ руху; Prm = εs/εq Ц турбулентне число ѕрандтл€; εq Ц к≥нематичний коеф≥ц≥Їнт турбулентного переносу теплоти; “|, w|x осереднен≥ у час≥ локальн≥ значенн€ в≥дпов≥дно температури ≥ складовоњ швидкост≥ вздовж ос≥ х.
«г≥дно р≥вн€нь (10.60) ≥ (10.61), поперек турбулентноњ ст≥каючоњ пл≥вки теплота ≥ к≥льк≥сть руху перенос€тьс€ €к молекул€рним шл€хом, так ≥ за рахунок турбулентних пульсац≥й. ѕриймемо дл€ подальших викладок, що Prm=1, тобто εq = εs = ε.
ѕеренос теплоти через в≥льно ст≥каючу пл≥вку конденсату в≥дбуваЇтьс€ в умовах практично усталеноњ густини теплового потоку по товщин≥ пл≥вки, €кщо теплота переохолодженн€ безмежно мала в пор≥вн€нн≥ з теплотою фазового переходу, тобто дq/ду = 0. ” цьому раз≥ з (10.60) маЇмо:
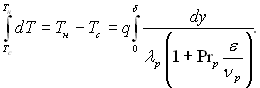
«в≥дси, враховуючи, що α = q/(“н Ц “с), отримаЇмо:
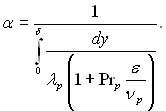 (10.62)
(10.62)
“аким чином, визначенн€ коеф≥ц≥Їнта теплов≥ддач≥ зводитьс€ до розрахунку ≥нтеграла, €кий стоњть в знаменнику р≥вн€нн€ (10.62).
¬иконан≥ розрахунки привод€ть до розрахунковоњ залежност≥, €ка справедлива при 1≤ Prp ≤ 25 ≥ 1,25Ј103 ≤ Re ≤ 6,9Ј104:
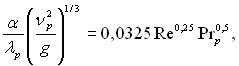 (10.63)
(10.63)
де α Ц м≥сцевий коеф≥ц≥Їнт теплов≥ддач≥, €кий маЇ найб≥льшу похибку розрахункових точок в≥д апроксимуючого р≥вн€нн€ до 12%.
ѕ≥д час розрахунку середнього коеф≥ц≥Їнта теплов≥ддач≥ дл€ вертикальноњ поверхн≥ необх≥дно врахувати, що у верхн≥й частин≥ маЇ м≥сце д≥л€нка лам≥нарноњ теч≥њ пл≥вки. «апишемо р≥вн€нн€ (10.8)
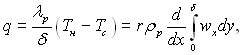
€ке в безрозм≥рному вид≥
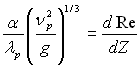
≥ враховуючи р≥вн€нн€ (10.63), отримаЇмо
![]()
” цьому р≥вн€нн≥ Z = Ga1/3(PrpK)Ц1. –озд≥лимо в останньому р≥вн€нн≥ зм≥нн≥ Re ≥ Z (вважаЇмо, що Prp = const) ≥ про≥нтегруЇмо в межах в≥д Zкр до Z ≥ в≥дпов≥дно в≥д Reкр до Re, матимемо:
![]()
–озвТ€зуючи це р≥вн€нн€ в≥дносно Re ≥ вважаючи, що Reкр = 400 ≥ Zкр = 2300, отримаЇмо наступний вираз:
![]() (10.64)
(10.64)
–≥вн€нн€ (10.64) описуЇ середн≥й коеф≥ц≥Їнт теплов≥ддач≥ дл€ вертикальноњ плоскоњ поверхн≥, на €к≥й маЇ м≥сце лам≥нарна ≥ турбулентна д≥л€нки теч≥њ конденсату. ÷€ формула отримана за умови, що ф≥зичн≥ параметри конденсату устален≥. ƒл€ урахуванн€ залежност≥ ф≥зичних параметр≥в в≥д температури доц≥льно коеф≥ц≥Їнт 0,024 множити на поправку (Prн/Prc)0,25, де ≥ндекси УнФ ≥ УсФ означають, що число ѕрандтл€ конденсату вибираЇтьс€ в≥дпов≥дно за температурами насиченн€ ≥ ст≥нки. ѕри цьому вс≥ ≥нш≥ ф≥зичн≥ параметри конденсату, що вход€ть в (10.64) повинн≥ вибиратис€ за температурою насиченн€. ” приведеному р≥шенн≥ прийн€то, що конвективн≥ складов≥ в р≥вн€нн≥ енерг≥њ ≥ ≥нерц≥йн≥ в р≥вн€нн≥ руху дор≥внюють нулю.
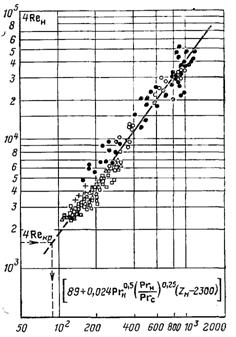
–ис.10.11. “еплов≥ддача при пл≥вков≥й конденсац≥њ нерухомоњ пари при зм≥шаному (лам≥нарному ≥ турбулентному) режим≥ руху пл≥вки конденсату (Reкр =400): ∆ Ц вода, Ќ=3,66 м, ћайсенбург;£Ц вода, Ќ=6,1 м,—тробе;Щ Ц вода, Ќ=2,9 м, Ўал≥ков; r Ц вода, Ќ=3,66 м, √еббард;Ш Ц дифен≥л, Ѕаджер
ѕор≥вн€нн€ формули (10.64) з досл≥дними даними наведено на рис. 10.11.
якщо задана густина теплового потоку на ст≥нц≥, враховуючи, що ![]() формулу (10.64) зручно застосовувати у наступному перетвореному вид≥:
формулу (10.64) зручно застосовувати у наступному перетвореному вид≥:
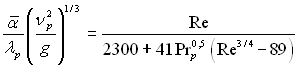 (10.65)
(10.65)
чи
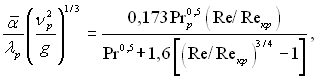 (10.66)
(10.66)
де Reкр число –ейнольдса, €ке в≥дпов≥даЇ переходу лам≥нарноњ теч≥њ пл≥вки до турбулентноњ.
якщо Re >>Reкр, тобто зона турбулентного режиму теч≥њ займаЇ б≥льшу частину поверхн≥, то
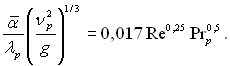 (10.67)
(10.67)
р≥м наведених, запропонований ще р€д формул дл€ розрахунку коеф≥ц≥Їнта теплов≥ддач≥ при турбулентн≥й теч≥њ пл≥вки конденсату. «апишемо формулу отриману —.—. утателадзе:
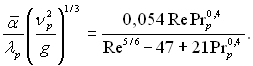 (10.68)
(10.68)
ѕри отриман≥ ц≥Їњ формули, вважалос€, що Reкр = 100.
ѕри Re > 2000 розрахунки можна виконувати за формулою:
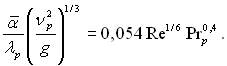 (10.69)
(10.69)
10.3. ¬плив перегр≥ву ≥ вологост≥ пари
Ќа цей час вплив вологост≥ ≥ перегр≥ву пари на ≥нтенсивн≥сть теплообм≥ну при конденсац≥њ вивчено недостатньо. Ќам≥тимо шл€хи п≥дходу до вир≥шенн€ задач≥ ≥ зробимо певн≥ оц≥нки.
онденсац≥€ перегр≥тоњ пари в≥дбуваЇтьс€, €кщо температура поверхн≥ ст≥нки нижче температури насиченн€. онденсуЇтьс€ пара, €ка охолоджена до температури насиченн€. ѕри цьому в обТЇм≥ пари в≥дбуваЇтьс€ конвективний теплообм≥н однофазного середовища, €кий ускладнюЇтьс€ поперечним потоком маси пари, що конденсуЇтьс€, Ц маЇ м≥сце немовби в≥дсмоктуванн€ пари в пл≥вку конденсату. —конденсована пара в≥ддаЇ пл≥вц≥ свою теплоту фазового переходу ≥ теплоту перегр≥ву. р≥м цього, конвективною теплов≥ддачею до пл≥вки п≥дводитьс€ частина теплоти не сконденсованоњ пари. «г≥дно (9.56)
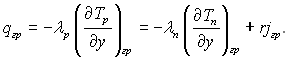
“аким чином, тепловий пот≥к в р≥дин≥ на поверхн≥ пл≥вки qгр = Цλр(д“р/ду)гр визначаЇтьс€ потоком теплоти фазового переходу rjгр ≥ конвективною теплов≥ддачею перегр≥тоњ пари qгр,пер = Цλп(д“п/ду)гр.. ќстанню складову можна представити так:
qгр,пер = q1 + q2. (10.70)
” цьому вираз≥ q1 = cpnθпер Ц теплота перегр≥ву сконденсованоњ пари; q2 Ц
теплота, €ка в≥ддаЇтьс€ не сконденсованою парою
—.—. утателадзе запропонував оц≥нювати зм≥ну коеф≥ц≥Їнта теплов≥ддач≥ за рахунок перегр≥ву за сп≥вв≥дношенн€м:
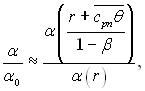 (10.71)
(10.71)
де
α Ц коеф≥ц≥Їнт теплов≥ддач≥
перегр≥тоњ пари; α0 Ц коеф≥ц≥Їнт теплов≥ддач≥ насиченоњ пари
при ≥нших р≥вних умовах; β ≈
q2/q. «г≥дно (10.71) у випадку конденсац≥њ перегр≥тоњ пари у в≥дпов≥дну формулу дл€ теплов≥ддач≥ насиченоњ пари п≥дставл€Їтьс€ зам≥сть r величина 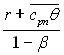 .
.
якщо пара волога, то при њњ конденсац≥њ волога, €ка м≥ститьс€ в н≥й, повн≥стю чи частково випадаЇ на поверхню пл≥вки. Ќа кожний к≥лограм пл≥вки конденсату приходитьс€ φ дор≥внюЇ одиниц≥ у раз≥ насиченоњ пари: дл€ вологоњ пари φ дор≥внюЇ чи трохи б≥льше (1 Ц х), де х Ц волог≥сть пари. ќц≥нювати коеф≥ц≥Їнт теплов≥ддач≥ можна п≥дстановкою у в≥дпов≥дне р≥вн€нн€ зам≥сть r величини φr. ќчевидно така оц≥нка маЇ найб≥льшу точн≥сть при невеликому вм≥сту вологи в нерухом≥й пар≥.
10.4. онденсац≥€ з нат≥канн€м конденсату
¬перше теплообм≥н горизонтальноњ труби при нат≥канн≥ конденсату з труб, що знаход€тьс€ вище, був досл≥джений Ќуссельтом. ¬ основу розрахунковоњ модел≥ Ќуссельта покладено у€вленн€ про те, що посл≥довне ст≥канн€ конденсату з труби на трубу т€гне за собою зб≥льшенн€ товщини пл≥вки конденсату ≥ в≥дпов≥дне зменшенн€ коеф≥ц≥Їнта теплов≥ддач≥ в нижн≥х трубах. «г≥дно теор≥њ Ќуссельта в≥дносний коеф≥ц≥Їнт теплов≥ддач≥ зм≥нюЇтьс€ по висот≥ вертикального р€ду горизонтально розташованих труб в≥д 0,7 дл€ другого р€ду пучка до 0,4 дл€ дванадц€того.
ƒосл≥ди ≥нших автор≥в не п≥дтверджують суттЇве пад≥нн€ коеф≥ц≥Їнта теплов≥ддач≥, висловлене Ќуссельтом. ќдною з причин р≥зниц≥ досл≥дних даних ≥ теор≥њ може бути та причина, що при скочуванн≥ конденсату на нижню трубу разом з ним передаЇтьс€ також ≥ певна к≥льк≥сть руху. ¬насл≥док цього негативний ефект скочуванн€ конденсату послабл€Їтьс€ ≥з-за прискоренн€ пл≥вки ≥ њњ подразнень.
¬и€вити вплив нат≥канн€ конденсату важко, €кщо досл≥джувати багатор€дний пучок, тому що у цьому випадку на ≥нтенсивн≥сть теплообм≥ну впливають ≥ ≥нш≥ чинники: швидк≥сть пари та ≥н. ¬ досл≥дах виконаних ¬.ѕ.≤саченком ≥ ј.‘.√лушковим конденсат скочувавс€ на нижню трубу з≥ зливноњ. Ќа верхн≥й тв≥рн≥й зливноњ труби були зроблен≥ отвори ≥ конденсат, €кий зливавс€ з них, був нагр≥тий до температури насиченн€. «ливна труба ставилас€ €к безпосередньо над досл≥дною (коридорна схема, в≥дносний крок s/d = 1,67), так ≥ з певним зм≥щенн€м вб≥к на половину д≥аметра (шахова схема). ¬ останньому випадку нижн€ тв≥рна зливноњ труби розм≥щувалас€ над боковою тв≥рною досл≥дноњ.

–ис.10.12. ¬плив нат≥канн€ конденсату на теплов≥ддачу горизонтальноњ труби: Щ Ц коридорна схема; £ Ц шахова схема
–езультати вим≥р≥в теплов≥ддач≥ наведен≥ на рис.10.12. коеф≥ц≥Їнт теплов≥ддач≥ α1 без нат≥канн€ зг≥дно тарувальних досл≥д≥в можна описати р≥вн€нн€м (10.35) з поправкою на зм≥нн≥ властивост≥ конденсату (10.43). Ќа ос≥ абсцис в≥дкладен≥ в≥дносн≥ витрати (Gзл + Gк)/Gк, де Gзл Ц витрати зливу; Gк Ц витрати конденсату, €кий утворивс€ на досл≥дн≥й труб≥. —уц≥льна л≥н≥€ в≥дпов≥даЇ отриман≥й досл≥дним шл€хом формул≥ —.Ќ.‘укса:
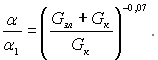 (10.72)
(10.72)
як сл≥дуЇ з рис.10.12, вплив викликаний нат≥канн€м конденсату на теплов≥ддачу пор≥вн€нно невеликий. Ќайб≥льше зменшенн€ коеф≥ц≥Їнта теплов≥ддач≥ складаЇ приблизно 30% ≥ в≥дпов≥даЇ в≥дносним витратам (Gзл + Gк)/Gк ≈ 15.
10.5. онденсац≥€ на ребристих поверхн€х
≈фективн≥сть ребристост≥ визначаЇтьс€ сп≥вв≥дношенн€м терм≥чних опор≥в ребра ≥ теплов≥ддач≥. ”мовами ефективност≥ ребристост≥ Ї:
дл€ довгих ребер 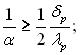 (10.73)
(10.73)
дл€ коротких ребер 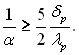 (10.74)
(10.74)
” цих р≥вн€нн€х λр Ц теплопров≥дн≥сть матер≥алу ребра; δр Ц товщина пр€мокутного ребра; α Ц коеф≥ц≥Їнт теплов≥ддач≥ до поверхн≥ ребра. ѕ≥д довгими ребрами розум≥ють так≥, дл€ €ких з достатн≥м наближенн€м справедливе у€вленн€ про одном≥рний розпод≥л температури вздовж ребра. ƒл€ коротких ребер це у€вленн€ не можна застосовувати ≥ варто виходити з у€ви просторового розпод≥лу температури у ребр≥.
—п≥вв≥дношенн€ (10.73) ≥ (10.74) запропонован≥, виход€чи з умови
![]()
де Q0 Ц к≥льк≥сть теплоти, що проходить кр≥зь основу ребра до ст≥нки; ℓ Ц довжина ребра (висота). —творювати ребра виг≥дно, €кщо dQ0/dℓ > 0, тобто коли тепловий пот≥к зб≥льшуЇтьс€ з≥ зб≥льшенн€м довжини ребра. ”мова dQ0/dℓ < 0 в≥дпов≥даЇ зменшенню теплового потоку з≥ зб≥льшенн€м довжини ребра. ¬ останньому випадку робити ребристою поверхню невиг≥дно.
ѕл≥вкова конденсац≥€ вод€ноњ пари зазвичай даЇ висок≥ коеф≥ц≥Їнти теплов≥ддач≥. ќц≥нюючи коеф≥ц≥Їнт теплов≥ддач≥ величиною пор€дку 104 ¬т/(м2Ј ), отримуЇмо з (10.74), що ефективна товщина ребра з м≥д≥ [λ ≈ 380 ¬т/(мЈ )] становить δр< 13 мм, дл€ латун≥ [λ ≈ 85 ¬т/(мЈ )] становить δр< 3 мм, дл€ титану [λ ≈ 15 ¬т/(мЈ )] Ц δр< 0,5 мм.
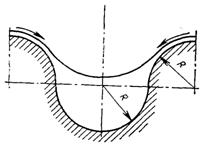
–ис.10.13. ѕроф≥ль хвил€стоњ поверхн≥ теплообм≥ну
оли ребра товщиною пор€дку 1 мм кр≥м звичайного ефекту зб≥льшенн€ теплового потоку за рахунок росту поверхн≥ конденсац≥њ виникаЇ можлив≥сть зб≥льшенн€ коеф≥ц≥Їнта теплов≥ддач≥, обумовлена д≥Їю сил поверхневого нат€гу. ќдин ≥з спри€тливих дл€ цього типу ребристоњ поверхн≥ наведений на рис.10.13.
ѕоверхн€ пл≥вки на виступах випукла, а на впадинах Ц вв≥гнута. ¬насл≥док цього зг≥дно р≥вн€нню (8.29) при достатньо мал≥й величин≥ рад≥уса R сили поверхневого нат€гу створюють великий град≥Їнт тиску, п≥д д≥Їю €кого конденсат, що утворивс€ на виступ≥, ст≥каЇ до впадини. Ќа виступ≥ залишаЇтьс€ пл≥вка, €ка маЇ м≥н≥мальний терм≥чний оп≥р. онденсат, €кий накопичуЇтьс€ у впадин≥, ст≥каЇ вниз п≥д д≥Їю сили т€ж≥нн€. ƒл€ забезпеченн€ стоку конденсату проф≥ль поверхн≥ труб виконуЇтьс€ у вигл€д≥ повздовжн≥х жолобк≥в ≥ виступ≥в, у горизонтальних труб Ц у вигл€д≥ нар≥зки з др≥бним кроком ≥ з плавно округленим проф≥лем.
“овщина пл≥вки в западин≥ може бути б≥льшою, н≥ж на виступ≥, але за в≥дпов≥дних умов середн≥й по поверхн≥ коеф≥ц≥Їнт теплов≥ддач≥ виходить б≥льшим, н≥ж дл€ гладкоњ поверхн≥.
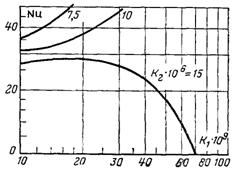
–ис.10.14. “еплов≥ддача вертикальноњ труби з проф≥льною поверхнею
–озгл€нутий метод ≥нтенсиф≥кац≥њ теплов≥ддач≥ вперше описаний –.√регор≥. ¬ивчаючи теплов≥ддачу при конденсац≥њ на вертикальн≥й труб≥ з рад≥усом кривизни проф≥лю виступу б≥л€ 0,6 мм, в≥н показав, що ≥нтенсивн≥сть теплов≥ддач≥ проф≥льноњ труби зб≥льшуЇтьс€ в пор≥вн€нн≥ з гладкою. Ќа рис.10.14 наведена теоретична залежн≥сть дл€ теплов≥ддач≥, де прийн€то:  јвтор пов≥домл€Ї, що досл≥дн≥ значенн€ задов≥льно сп≥впадають з розрахунковою залежн≥стю.
јвтор пов≥домл€Ї, що досл≥дн≥ значенн€ задов≥льно сп≥впадають з розрахунковою залежн≥стю.
’арактерною особлив≥стю конденсац≥њ на вертикальних трубах з др≥бними хвил€ми поверхн≥ Ї р≥зке зменшенн€ коеф≥ц≥Їнта теплов≥ддач≥ в нижн≥й частин≥ труби, обумовлене затопленн€м виступ≥в ст≥каючим конденсатом. Ќаприклад, при конденсац≥њ вод€ноњ пари при атмосферному тиску ≥ Δ“ = 20 повне затопленн€ виступ≥в в≥дбуваЇтьс€ в к≥нц≥ труби на довжин≥ б≥л€ 1,5 м.
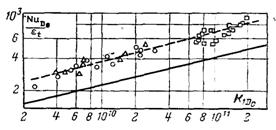
–ис.10.15. ѕор≥вн€нн€ теплов≥ддач≥ при конденсац≥њ на горизонтальн≥й труб≥ з гладкою ≥ хвил€стою поверхн€ми: K1Do = GaDoKPr; Щ Ц R=0,5 мм, D0=10 мм; r Ц R=0,25 мм, D0=10 мм;£ Ц R=0,34 мм, D0=21 мм
¬иконан≥ досл≥дженн€ теплов≥ддач≥ горизонтальноњ труби з др≥бним хвильовим проф≥лем поверхн≥, отриманих нар≥зкою р≥зьби з малим кроком ≥ плавно округленим проф≥лем (рис.10.13). –ад≥уси кривизни R виступ≥в дл€ трьох досл≥дних труб складали 0,5; 0,25 ≥ 0,34 мм. Ќа рис.10.15 наведен≥ результати досл≥д≥в, виконаних з вод€ною парою при тиску в≥д 0,0294 до 0,098 ћѕа (в≥д 0,3 до 1,0 кгс/см2). “емпературний нап≥р зм≥нювавс€ в≥д 5 до 40 . —уц≥льна л≥н≥€ на рис.10.15 описуЇтьс€ р≥вн€нн€м (10.34), в €кому за визначальний розм≥р вибраний д≥аметр труби по впадинах D0. ƒосл≥дн≥ значенн€ коеф≥ц≥Їнт≥в теплов≥ддач≥ в≥днесен≥ до повноњ зовн≥шньоњ поверхн≥ ребристоњ труби.
10.6. онденсац≥€ з в≥дсмоктуванн€м конденсату
¬≥дсмоктуванн€ утворюваного конденсату в пористу ст≥нку зменшуЇ товщину пл≥вки, що спри€Ї зб≥льшенню коеф≥ц≥Їнта теплов≥ддач≥. “еплообм≥н на вертикальн≥й ст≥нц≥ ≥ горизонтальн≥й труб≥ з пост≥йною швидк≥стю в≥дсмоктуванн€ анал≥зувавс€ в р€д≥ роб≥т. ” теор≥њ було прийн€то, що температура поверхн≥ пористоњ ст≥нки пост≥йна. ѕара чиста, насичена. ”с≥ ф≥зичн≥ параметри €к р≥дини, так ≥ пари вважалис€ усталеними. „астина конденсату видал€Їтьс€ в≥дсмоктуванн€м, у той час €к залишкова частина утворюЇ р≥дку пл≥вку, €ка ст≥каЇ п≥д д≥Їю сил т€ж≥нн€. ѕри цьому враховувалис€ ≥нерц≥йн≥ сили.
ѕл≥вка спов≥льнюЇ св≥й рух завд€ки силам вТ€зкост≥. р≥м терт€ на ст≥нц≥ враховувавс€ оп≥р терт€ на поверхн≥ розд≥лу р≥дкоњ ≥ паровоњ фаз. ¬важалос€, що пара нерухома на достатн≥й в≥дстан≥ в≥д ст≥нки. ≤нтегральн≥ р≥вн€нн€ к≥лькост≥ руху ≥ енерг≥њ, записан≥ стосовно умов задач≥, розвТ€зувалис€ р≥зними методами.
ѕри конденсац≥њ на вертикальн≥й порист≥й ст≥нц≥ м≥сцевий коеф≥ц≥Їнт теплов≥ддач≥ можна описати залежн≥стю:
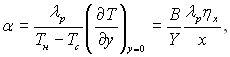 (10.75)
(10.75)
де 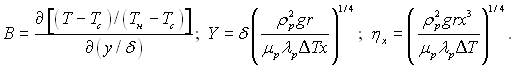
Ћокальне число Ќуссельта:
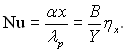
–озрахунки були виконан≥ в област≥ чисел ѕрандтл€ в≥д 10Ц3 до 50; 0,01 < x < 1 ≥ 10Ц5 < 1/K < 10Ц1 дл€ р≥зних значень х/Ќ, де Ќ Ц висота ст≥нки. –озрахунки показали, що застосуванн€ в≥дсмоктуванн€ приводить до зб≥льшенн€ теплов≥ддач≥. ” безрозм≥рн≥й форм≥ запису ≥нтенсивн≥сть в≥дсмоктуванн€ становить:
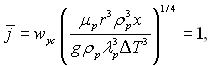
що в≥дпов≥даЇ ψ= 4,63 (де ψ Ц в≥дношенн€ к≥лькост≥ конденсату, що в≥дсмоктуЇтьс€ до к≥лькост≥ конденсату, що ст≥каЇ по ст≥нц≥). “еплов≥ддача в пор≥вн€нн≥ з випадком без в≥дсмоктуванн€ зб≥льшуЇтьс€ на 50%. ” цьому р≥вн€нн≥ wyc Ц л≥н≥йна швидк≥сть в≥дсмоктуванн€. –≥ст числа Ќуссельта за рахунок в≥дсмоктуванн€ зб≥льшуЇтьс€ з в≥дстанню вниз за потоком.
« асимптотичного розвТ€зку сл≥дуЇ, що на в≥дстан≥ в≥д верхньоњ кромки
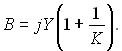 (10.76)
(10.76)
ƒл€ цього випадку
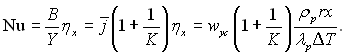 (10.77)
(10.77)
ќтже, на великих в≥дстан€х в≥д верхньоњ кромки величина числа Ќуссельта не залежить в≥д числа ѕрандтл€ ≥ пропорц≥йна швидкост≥ в≥дсмоктуванн€. ¬плив переохолодженн€ конденсату, €кий ураховуЇтьс€ 1+(1/ ), оказуЇтьс€ несуттЇвим при >> 1
–≥шенн€ дл€ горизонтальних труб також показуЇ, що в≥дсмоктуванн€ конденсату спри€Ї зб≥льшенню теплов≥ддач≥.
¬ ≥нженерн≥й практиц≥ дл€ ≥нтенсиф≥кац≥њ теплов≥ддач≥ з боку пари, що конденсуЇтьс€, ≥нколи застосовують пром≥жне в≥дведенн€ конденсату. Ќа вертикальних ст≥нках ставл€тьс€ похил≥ пластини чи ковпаки, €к≥ в≥двод€ть утворений конденсат. Ќижче ковпака пл≥вка знову починаЇ утворюватис€. “аким чином, середн≥й коеф≥ц≥Їнт теплов≥ддач≥ зб≥льшуЇтьс€, завд€ки зменшенню середньоњ товщини пл≥вки.
« формули (10.14) виходить, що к≥льк≥сть конденсатов≥дв≥дних ковпак≥в п при заданому в≥дносному зб≥льшенн≥ середнього коеф≥ц≥Їнта теплов≥ддач≥ α\h/α\H можна визначити з р≥вн€нн€:
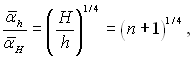 (10.78)
(10.78)
де Ќ Ц висота ст≥нки; h в≥дстань м≥ж ковпаками по вертикал≥; α\H Ц коеф≥ц≥Їнт теплов≥ддач≥ без установки ковпак≥в; α\hЦ коеф≥ц≥Їнт теплов≥ддач≥ п≥сл€ установки ковпак≥в.
ƒ≥аметр ковпака вибираЇтьс€ з умови, щоб ст≥каючий з його кромки конденсат не потрапл€в на ст≥нку, €ка знаходитьс€ нижче ковпака. ћал≥ виступи конденсат може обт≥кати €к елементи шорсткост≥, що зменшуЇ швидк≥сть ст≥канн€ лам≥нарноњ пл≥вки.
ќц≥нимо рад≥ус R крапл≥, €ка ст≥каЇ з нахиленоњ поверхн≥. ѕл≥вка на кромц≥ утворюЇ валик, що викликано силами поверхневого нат€гу. ƒал≥ в≥дбуваЇтьс€ згортанн€ валика в краплю ≥ њњ пад≥нн€. «г≥дно я.≤.‘ренкелю рух п≥д час переливанн€ нагадуЇ рух гусениц≥ трактора. —прощена схема цього руху показана на рис.10.16.
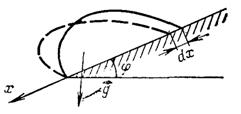
–ис.10.16. —хема скатуванн€ крапл≥ з похилоњ поверхн≥
ƒл€ простоти будемо вважати, що скочуЇтьс€ цил≥ндричний валик п≥д д≥Їю сил т€ж≥нн€, €ким чин€ть оп≥р кап≥л€рн≥ сили.
≈лементарна робота сил т€ж≥нн€, в≥днесена до одиниц≥ довжини валика, при зм≥щенн≥ на dx становить:
![]()
де т Ц маса валика, кг/м.
≈лементарна робота кап≥л€рних сил:
![]()
де Δσ Ц питома робота кап≥л€рних сил, ƒж/м2.
ѕрир≥внюючи прав≥ частини двох останн≥х р≥вн€нь, отримаЇмо, що
![]() (10.79)
(10.79)
«г≥дно формули ƒюпре величину Δσ можна виразити р≥вн€нн€м:
![]() (10.80)
(10.80)
де ≥ндексами УрФ, УпФ, УтФ позначен≥ в≥дпов≥дно р≥дина, пара ≥ тверде т≥ло. ¬еличини
σтп ≥
σрт не можна визначити пр€мими вим≥рами. ” першому наближенн≥ можна поступити таким чином. ƒл€ контуру, сп≥льного дл€ трьох фаз, можна використати формулу Ќеймана ![]() справедливу дл€ випадку р≥вноваги, коли система знаходитьс€ т≥льки п≥д д≥Їю кап≥л€рних сил. «в≥дси виходить, що
справедливу дл€ випадку р≥вноваги, коли система знаходитьс€ т≥льки п≥д д≥Їю кап≥л€рних сил. «в≥дси виходить, що
![]()
де θ Ц крайовий кут змочуванн€.
ѕ≥дставл€ючи значенн€ σтп у вираз (10.80) дл€ Δσ, отримаЇмо
![]() (10.81)
(10.81)
ѕитому масу валика у момент скочуванн€ т визначаЇмо з р≥вн€нн€:
![]()
ѕ≥дстановка цього виразу в р≥вн€нн€ (10.79) даЇ:
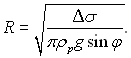 (10.82)
(10.82)
¬еличину Δσ можна визначити за (10.81), €кщо р≥дина добре змочуЇ поверхню, у цьому раз≥ в першому наближенн≥ cosθ = 1 ≥ Δσ = 2σрп.
якщо вважати, що р≥дина скочуЇтьс€ не в вигл€д≥ валика, а у вигл€д≥ крапл≥, то внасл≥док наближених розрахунк≥в, под≥бним до виконаних, можна отримати формулу виду (10.82), але в н≥й п≥д знаком радикалу зТ€витьс€ додатковий множник 3/2.