Розділ 11. ТЕПЛООБМІН ПРИ ПЛІВКОВІЙ КОНДЕНСАЦІЇ РУХОМОЇ ПАРИ
11.1. Міжфазне тертя
Пара, яка конденсується, не може бути абсолютно нерухомою, тому що густина рідкої фази завжди відрізняється від густини пари. Пара, що конденсується на холодній поверхні, поповнюється новою, яка надходить з основної маси. Тому пара завжди знаходиться в русі, якщо її швидкість мала, то вона не чинить помітної динамічної дії на конденсат і може вважатися практично нерухомою.
У технічних пристроях часто реалізуються великі швидкості пари, що не дозволяє нехтувати її динамічною дією на конденсат. При цьому часто виникає спрямований повздовжній рух пари; сили тертя на міжфазній границі можуть бути значними.
Умови динамічної взаємодії пари і конденсату відтворюються рівнянням кількості руху для поверхні розриву (9.43). При плоско-паралельному ламінарному русі (див. § 9.2) рівняння кількості руху в проекції на нормаль до поверхні розриву має вид:
р1 = р2 + рσ,
а в проекції на дотичну до поверхні розділу – вид:
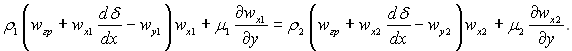
Для стаціонарної задачі при виконанні рівності wx1 = wx2 з останнього рівняння слідує, що
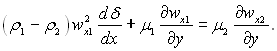(11.1)
Член 
показує ту обставину, що повздовжня складова швидкості wx не є дотичною до поверхні рідини. Для плівкової конденсації у наближенні пограничного шару
δ <<
ℓ і
dδ/dx → 0. Тоді
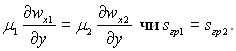(11.2)
Напругу тертя на поверхні розриву виразимо через коефіцієнт тертя сf:
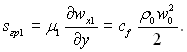(11.3)
У цьому рівнянні ρ0, w0 – характерна густина і швидкість у фазі 1 (наприклад, густина і швидкість пари на віддалі від поверхні конденсації).
Середнє значення напруги тертя при цьому можна виразити рівнянням
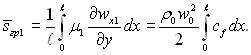(11.4)
Під час конденсації відбувається немов би відсмоктування пари через міжфазну границю. Просте рішення можна отримати при повздовжньому ламінарному обтіканні плоскої пластини з рівномірним розподілом відсмоктування при др/дх = 1 (рис.11.1).
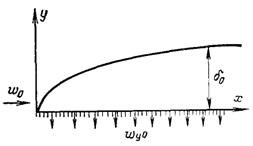
Рис.11.1. Повздовжнє обтікання плоскої пластини з рівномірно розподіленим відсмоктуванням
У цьому випадку течія в пограничному шарі описується рівняннями:
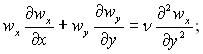(11.5)
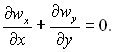(11.6)
Граничні умови:
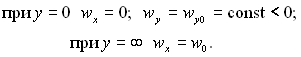
Система рівнянь (11.5), (11.6) має рішення, при якому розподіл швидкості не залежить від повздовжньої координати (дwx/дх = 0). Це рішення витікає з умови, згідно якої завжди можна підібрати таку швидкість відсмоктування wу0, яка буде дорівнювати wуδ(х) надходження рідини (пари) із зовнішнього потоку в пограничний шар (плівку рідини).
У випадку коли дwx/дх = 0 з рівняння нерозривності потоку (11.6) виходить, що wy(x, y) = wy0 = const, і рівняння (11.5) набуває вигляду:
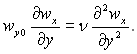
Рішення цього рівняння за умови, коли wy0 < 0 буде:
wx(y) = w0[1– exp(wy0y/ν)]. (11.7)
Розподіл швидкості досягає такого простого виду тільки асимптотично – після того, як потік пройде вздовж пластини початкову ділянку і товщина пограничного шару досягне певної величини
δ0. Картина ліній току при повздовжньому обтіканні плоскої пластини з рівномірним розподілом відсмоктування наведена на рис.11.2. Асимптотичний розподіл швидкості (11.7) досягається після проходження початкової ділянки, безрозмірна довжина якої становить: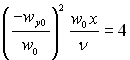 
чи
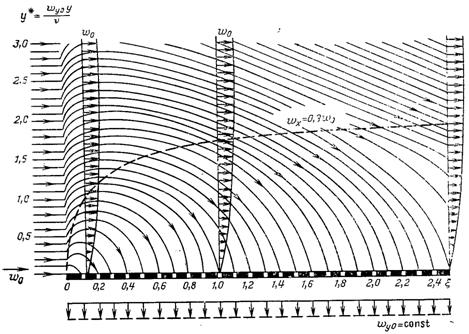
Рис.11.2. Лінії току при повздовжньому обтіканні плоскої пластини з рівномір-ним розподілом відсмоктування:
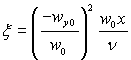
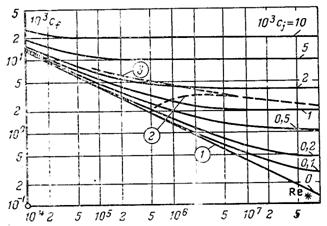
Рис.11.3. Коефіцієнт опору сf плоскої пластини, яка обтікає у повздовжньому напрямку ламінарним потоком з рівномірно розподіленим відсмоктуванням у стінку при різних значеннях коефіцієнта витрат сf = (–wy0)/w0; 1, 2, 3 (цифри в колах) – без відсмоктування: 1 – при ламінарній течії; 2 – для перехідного із ламінарного до турбулентного; 3 – для повністю турбулентної течії
На рис.11.3 наводяться криві залежності коефіцієнта опору від числа Рейнольдса для пластини з рівномірним розподілом відсмоктування. При великих числах Рейнольдса опір визначається законом:
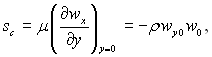(11.8)
згідно з яким напруга тертя не залежить від в’язкості.
Рівняння (11.8) можна представити в іншому виді:
(11.9)
де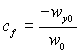 
– коефіцієнт витрат (wy0 = const).
Опір, який визначається рівнянням (11.9), називається опором стоку і обумовлене переносом кількості руху зовнішнього потоку зі швидкістю w0, з поперечним потоком маси jгр = ρwy0. При малих числах Рейнольдса коефіцієнт опору більший (див. рис.11.3). На початковій частині пластини, де формується пограничний шар, дотичні напруги більші, ніж на відстані, і залежать від числа Рейнольдса. Тут мають місце і молекулярні в’язкі сили. Дотичні напруги при цьому можна представити у вигляді суми двох складових:
(11.11)
де коефіцієнт тертя сf = c*f + 2cj поданий як результуюча величина. Складова c*f обумовлена в’язкими молекулярними силами.
Розглянуті у цьому параграфі результати отримані на основі наближень в пограничному шарі. Для того щоб при течії з відсмоктуванням виконувалися допущення, які лежать в основі теорії пограничного шару, швидкість відсмоктування wy0 повинна бути не більше величини порядку w0/Rex0,5. При числі Reх = 106 ця умова дає для швидкості wy0 значення wy0 =0,001w0. У цьому випадку кількість висмоктаної рідини настільки мала, що з пограничного шару виходять тільки частинки рідини, які знаходяться безпосередньо біля стінки. Виходячи з умови незначності wy0 у порівнянні з w0, можна назвати верхню межу коефіцієнта витрат
wy0/w0 ≤ 0,01.
При конденсації “висмоктування” пари йде мимовільно, зміна інтенсивності по довжині регулюється відповідними змінами термічних опорів. Вважаючи, що при конденсації пари на пластині величина “висмоктування” jгр вздовж плівки змінюється, для визначення тертя на границі пара – рідина можна використати рівняння (11.8), представивши його в такому виді:
(11.12)
де (wn0 – wδ) – швидкість пари на відстані, відлічена від швидкості поверхні плівки wx(δ) = wδ; jгр – густина потоку маси пари, що конденсується, при у = δ. Величина dδ/dx при цьому вважається малою.
Розрахунки показують, що у багатьох задачах, які мають прикладне значення sj >> c*f . У випадку малих чисел Рейнольдса Rex = w0x/ν використання (11.12) можна поставити під сумнів.
Під час конденсації пари у технічних пристроях його швидкість часто не залишається постійною при течії вздовж охолоджувальної поверхні. Наприклад, при повній конденсації пари в трубі її витратна швидкість може змінюватися від максимального значення wn0 на вході до нуля на виході з труби. У загальному випадку при цьому актуальні як граничні сили в’язкості, так і опір виходу з труби. Крім цього, рух двофазного середовища ускладнюється у зв'язку із супутніми ефектами, які мають місце при конденсації пари, що рухається з великою швидкістю.
Рішення задач тепло і масообміну і тертя при обтіканні проникливої поверхні турбулентним пограничним шаром виконано рядом дослідників, які виходили з того, що в неоднорідному за своїми характеристиками турбулентному потоці, який обмиває стінку, найбільш стійкою по відношенню до зовнішніх подразників є область пристінної турбулентності, яка знаходиться безпосередньо біля стінки твердого тіла, але поза областю в’язкого підшару.
Зміни умов на твердій поверхні суттєво впливають на в’язку частину течії, де переважає вплив молекулярного переносу кількості руху. Зміна умов течії в не подразненому потоці проявляється передусім у зовнішній області турбулентного пограничного шару.
Розміри в’язкої області зменшуються зі зменшенням молекулярної в’язкості швидше, ніж розміри усього турбулентного пограничного шару. В зв'язку з цим можна розглядати деякий ідеальний турбулентний пограничний шар з виродженим в’язким підшаром. У такому пограничному шарі інтегральні характеристики переносу кількості руху, теплоти і маси визначаються властивостями турбулентного пристінного ядра. Отримані результати можна, в певній мірі, використовувати для розрахунку реальних течій.
У випадку коли cf = const і за постійного числа Рейнольдса, при обмиванні проникливої пластини турбулентним пограничним шаром коефіцієнт тертя описується наступною залежністю:
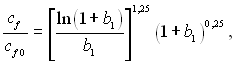(11.13)
де cf0 – коефіцієнт тертя при омиванні непроникливої поверхні; b1 = (wy0/w0)(2/cf0) – параметр проникливості.
Для граничного випадку інтенсивного відсмоктування дотична напруга тертя на проникливій поверхні визначається по формулі:
s = ρwy0,
тобто аналогічно випадку ламінарної течії. Таким чином, гранична залежність (11.12) має місце при будь-якому режимі течії пари.
