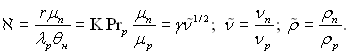11.2. Конденсація на плоскій пластині
Розглянемо течію плівки і теплообмін при повздовжньому омиванні пластини парою за умови її конденсації. Теплообмін при конденсації рухомої пари у загальному випадку повинен визначатися рішенням спряженої задачі. Рівняння, які необхідні для її формулювання, наводяться в розділі 9. Оскільки спряжену задачу не завжди можна розв’язати достатньо повно, не втратили значення і підходи до розв’язку задачі, в яких взаємодія конденсату з сусідніми фазами ураховується через наперед заданими граничними умовами.
Вважаємо рух плівки вздовж плоскої поверхні, ламінарним. Товщина плівки δ мала в порівнянні з її довжиною ℓ вздовж течії, що дозволяє використати наближеннями в пограничному шарі. Потік пари, що набігає на плівку, спрямований вздовж неї у сторону збільшення координати х. Ось у нормальна до поверхні пластини. Початок координат знаходиться на передній кромці пластини.
Розглянемо найпростіший варіант формулювання задачі про течію плівки. Нехтуючи інерційними силами, рівняння руху для плоскої течії можна записати в наступному виді:
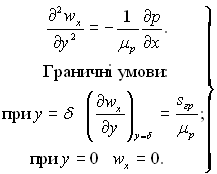 (11.14)
(11.14)
У формулі (11.14) величина др/дх може враховувати гідростатичну складову тиску ρрgx чи (ρр – ρп)gx, якщо густина пари співрозмірна з густиною рідини. Інтегрування по у показує, що
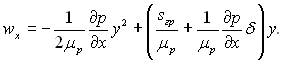 (11.15)
(11.15)
Профіль швидкості у плівці описується квадратичною параболою. Якщо (др/дх)δ << sгр, то розподіл буде лінійним:
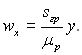
Витрати рідини G, кг/с, через поперечний переріз плівки:
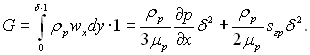 (11.16)
(11.16)
Під час конденсації витрати змінюються вздовж плівки. Нехтуючи переохолодженням конденсату температури насичення, зміну витрат можна представити наступною залежністю:
![]()
Підставляючи сюди значення витрат згідно рівнянню (11.16), отримаємо:
![]() (11.17)
(11.17)
Якщо др/дх = const і sгр = const, з останнього рівняння маємо:
![]() (11.18)
(11.18)
Теорію теплообміну при ламінарній плівковій конденсації рухомої пари вперше запропонував В.Нуссельт (1916 р.). Задача розв’язувалася при тих же допущеннях, що і для конденсації нерухомої пари (§ 10.1), але напруга тертя на поверхні плівка – пара не вважалася рівною нулю.
Розв’язок рівняння d2T/dy2 = 0 при граничних умовах Т(0) = Тс і Т(δ) = Тн буде
![]()
чи
![]()
Граничне тертя В.Нуссельт задав згідно рівнянню
![]() (11.19)
(11.19)
де wn0 = const. Течія пари вважалася без градієнтною. Сила тяжіння враховувалася виразом
![]() (11.20)
(11.20)
де β – кут, утворений пластиною і горизонтальною площиною. Тоді згідно рівнянню (11.15) профіль швидкості у конденсаті буде:
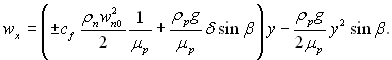 (11.21)
(11.21)
Середня швидкість плівки становить:
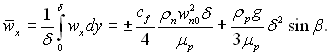 (11.22)
(11.22)
У подальшому розглядується конденсація на вертикальній стінці (β = 90°). Введемо позначення:
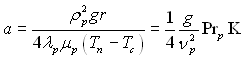 (11.23)
(11.23)
і
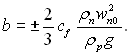 (11.24)
(11.24)
Вважаємо рух пари і плівки супутній (b > 0), при цьому рішення рівняння (11.18) буде:
![]() (11.25)
(11.25)
(під час інтегрування використана умова, згідно з якою при х = 0 δ = 0).
Якщо wn0 = 0, то b = 0 і тоді отримуємо рівняння (10.9)
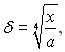
яке справедливе для нерухомої пари.
При великих значеннях b (при 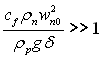 ) рівняння (11.25) набуває виду:
) рівняння (11.25) набуває виду:
![]() (11.26)
(11.26)
Звідси слідує, що для пари, яка швидко рухається, сили тертя актуальні і ними не можна нехтувати,
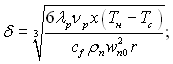 (11.27)
(11.27)
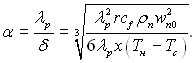 (11.28)
(11.28)
Середньо інтегральний коефіцієнт тепловіддачі при цьому:
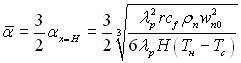 (11.29)
(11.29)
чи
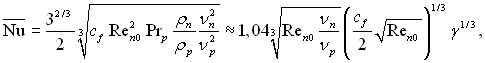 (11.30)
(11.30)
де 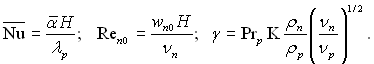
У випадку, коли сила тертя і тяжіння співрозмірні, необхідно використовувати рівняння (11.25). Це рівняння має тільки дійсні корні. Якщо позначити
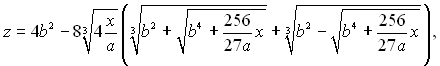
то корні можна записати в наступному виді:
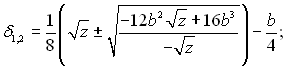
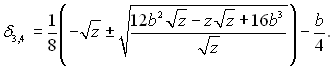
Середній коефіцієнт тепловіддачі для стінки висотою Н:
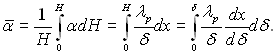
Для dx/dδ з (11.25) маємо:
![]()
Підставляючи dx/dδ і після інтегрування, отримаємо:
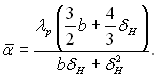 (11.31)
(11.31)
У цьому рівнянні δН = δ(Н) є додатним коренем рівняння (11.25) при х = Н. Рівняння (11.31) можна записати в наступному виді:
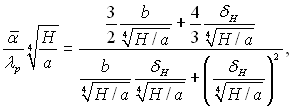 (11.32)
(11.32)
тоді рівняння (11.25) при х = Н, буде:
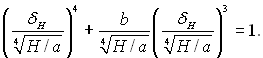 (11.33)
(11.33)
З рівнянь (11.32), (11.33) виходить, що 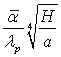 є функцією
є функцією ![]() :
:
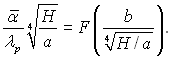 (11.34)
(11.34)
Нуссельт розрахував значення функції F.
Якщо пара рухається вздовж пластини з низу вгору, тобто проти напрямку сили тяжіння (b < 0), то
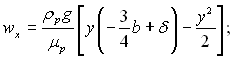 (11.35)
(11.35)
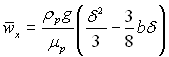 (11.36)
(11.36)
і
![]() (11.37)
(11.37)
При великій швидкості пари, коли плівка тече вгору, затягуючись парою, сталу інтегрування можна визначити з умови, згідно з якою при х = Нδ = 0. Тоді для товщини плівки отримуємо рівняння
![]() (11.38)
(11.38)
Середній коефіцієнт тепловіддачі
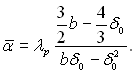 (11.39)
(11.39)
У цьому рівнянні δ0 – товщина плівки на верхньому кінці пластини, ця величина є найменшим дійсним коренем рівняння (11.38) при х = 0. Рішення дійсне при
![]()
і, як наслідок, придатне для швидкості
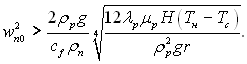 (11.40)
(11.40)
Якщо швидкість пари менша значення, яке визначається формулою (11.40), то тертя рухомої пари недостатньо, щоб затягнути весь конденсат вгору. Згідно рішенню Нуссельта частина конденсату може рухатися вгору і частина – вниз. Внаслідок цього товщина плівки повинна бути змінною. При х = 0 вона дорівнює
δ = (3/4)b і монотонно зменшується на інтервалі від х = 0 до х = х1 = (27/256)b4а, де вона рівна нулю. Конденсат, який утворюється при x
Якщо рівність (11.40) не виконується, рішення Нуссельта набуває умовного характеру пов’язаного з фізично важко пояснювальним стрибком товщини плівки при х=х1. Крім цього умова ламінарного руху може не виконуватися. У своїй роботі Нуссельт приводить таблицю функції
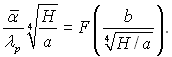
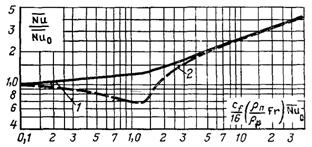
Рис.11.4. Відносна тепловіддача при плівковій ламінарній конденсації на вертикальній плоскій пластині згідно з рішенням Нуссельта: 1 – супутній рух пари у плівці з верху вниз; 2 – рух пари вгору
На рис.11.4 наведені розрахункові дані середньої тепловіддачі у вигляді залежності:
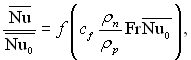
де ![]() – число Нуссельта для пари, що рухається з великою швидкістю;
– число Нуссельта для пари, що рухається з великою швидкістю; ![]() – число Нуссельта для нерухомої пари, що розраховується по залежності:
– число Нуссельта для нерухомої пари, що розраховується по залежності:
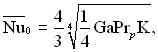
в якій 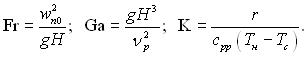
Суцільною лінією показана тепловіддача під час руху пари вниз, пунктирною – вгору. Приблизно при 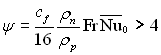 напрямок руху пари не впливає на інтенсивність теплообміну, що відповідає дуже малому впливу сили тяжіння у порівнянні з міжфазним тертям. Тепловіддача при цьому описується рівняннями (11.28) і (11.29).
напрямок руху пари не впливає на інтенсивність теплообміну, що відповідає дуже малому впливу сили тяжіння у порівнянні з міжфазним тертям. Тепловіддача при цьому описується рівняннями (11.28) і (11.29).
При зустрічному напрямку течії пари і сили тяжіння тепловіддача проходить через мінімум. Мінімуму відповідає ψ = 1,33. Якщо ψ > 1,33, конденсат, який затягується парою, рухається вгору. Як слідує з розрахунків Нуссельта, при р = 0,098 МПа (1 кгс/см2), ΔТ = 10 К уся плівка тече вгору, якщо швидкість водяної пари перевищує 40 м/с.
Нуссельт розглядав плівкову конденсацію за умови Тс = const. Якщо qс = = const, то згідно (10.8) можна записати:
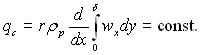
Розподіл швидкості по товщині плівки wx(y) можна визначити з рівняння руху d2wx/dy2 = –ρpg/μp при граничних умовах wx(0) = 0 і d2wx(δ) /dy2 = = ±(cf /μp)(ρpg/2). Згідно (11.17) маємо:
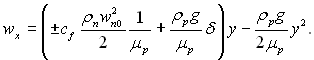
Тоді
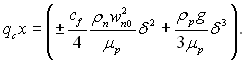 (11.41)
(11.41)
Якщо 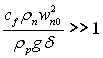 , отримуємо:
, отримуємо:
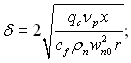 (11.42)
(11.42)
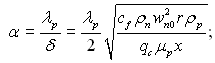 (11.43)
(11.43)
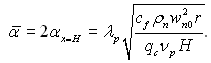 (11.44)
(11.44)
Рівняння (11.44) можна представити у безрозмірній формі запису
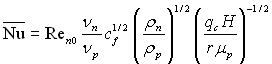
чи, ураховуючи, що 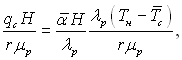
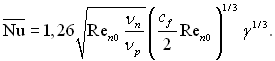 (11.45)
(11.45)
У цьому випадку число фазового переходу К визначається за середнім температурним напором ![]() Порівняння рівнянь (11.30) і (11.45) показує, що у випадку пари, яка швидко рухається
Порівняння рівнянь (11.30) і (11.45) показує, що у випадку пари, яка швидко рухається 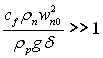 при qc = const середній коефіцієнт тепловіддачі більший, ніж у випадку при Тс = const. Згідно з формулами (11.30) і (11.45) залежність середнього коефіцієнта тепловіддачі від швидкості однакова при обох використаних граничних умовах.
при qc = const середній коефіцієнт тепловіддачі більший, ніж у випадку при Тс = const. Згідно з формулами (11.30) і (11.45) залежність середнього коефіцієнта тепловіддачі від швидкості однакова при обох використаних граничних умовах.
У рішенні Нуссельта коефіцієнт тертя вважався усталеним і задавався наперед за даними експериментального дослідження Еберле. Більш повною варто вважати постановку задачі, коли тертя на поверхні розриву визначається з одночасного розгляду течії в паровій і рідкій фазах. Основи постановки подібного роду спряжених задач розглянутих в розділі 9. У такій постановці задача вперше розв’язувалася Г.Г.Чорним (1954 р.)
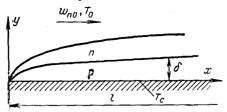
Рис.11.5. Ламінарна плівкова конденсація пари, яка швидко рухається (до постановки спряженої задачі)
Г.Г.Чорний розглядав ламінарну плівкову конденсацію пари, яка швидко рухається (рис.11.5), ґрунтуючись на диференціальних рівняннях, записаних у наближенні пограничного шару.
Для парової фази:
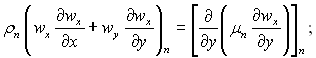
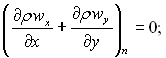
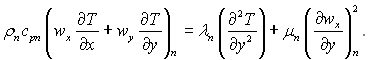
Для рідкої фази (конденсату):
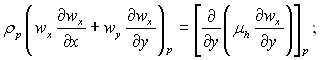
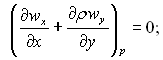
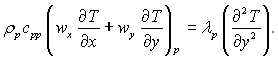
Для поверхні розриву пара – конденсат задавалися наступні умови:
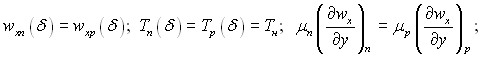
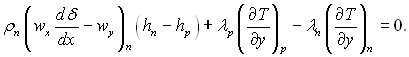
Граничні умови: ![]()
Система диференціальних рівнянь спрощується, якщо перейти до змінних:
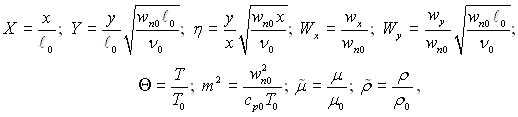
де індексом “0” позначені характерні масштаби і, задовольняючи рівняння нерозривності потоку, вводиться функція току наступними співвідношеннями
![]()
Позначивши 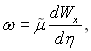 після певних перетворень рівняння руху і енергії, раніше записані, можна привести до виду:
після певних перетворень рівняння руху і енергії, раніше записані, можна привести до виду:
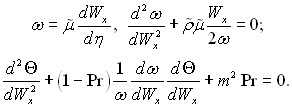
Ці рівняння, які необхідно записати для пари і конденсату, є звичайними диференціальними рівняннями.
Граничні умови і умови спряження при цьому:
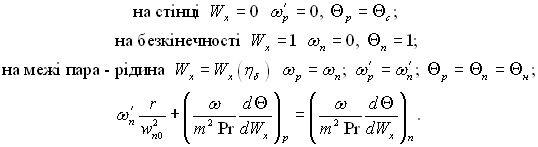
Функції ω(Wx) відшукувалися аналітичним шляхом в поєднанні з числовим інтегруванням. Розв’язок задачі доведено до квадратур. Функції ω(Wx) були зведені в таблиці. І все ж таки визначення полів динамічних і теплових величин по запропонованій методиці пов’язане з громіздкими розрахунками. Немає достатньої ясності стосовно меж застосування запропонованого розв’язку при інтенсивному поперечному потоці маси на границі розділу фаз, коли прийняті наближення пограничного шару можуть не виконуватися.
У загальному випадку розв’язок отримано за певних додаткових спрощеннях задачі. Приймалося, що теплота тертя і теплота нагрівання пари невеликі в порівнянні з теплотою фазового переходу. Фізичні параметри усталені, при цьому для пари Pr = 1. Для середнього коефіцієнта тепловіддачі запропонована формула:
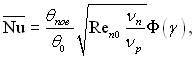 (11.46)
(11.46)
де 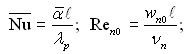 ℓ – довжина пластини;
ℓ – довжина пластини; ![]() – відношення перепаду температури у плівці до повного перепаду температури по
товщині парового пограничного шару і плівки
θпов =
Тн – Тс,
θ0 =
Т0 – Тс. У разі конденсації насиченої пари
θпов/θ0 =
1 і
– відношення перепаду температури у плівці до повного перепаду температури по
товщині парового пограничного шару і плівки
θпов =
Тн – Тс,
θ0 =
Т0 – Тс. У разі конденсації насиченої пари
θпов/θ0 =
1 і
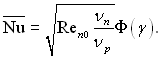 (11.47)
(11.47)
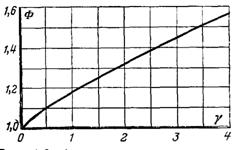
Рис.11.6. Залежність функції Ф від γ = PrpK(ρn/ρp)(νn/νp)0,5
Значення функції Ф(γ) представлені графічно на рис.11.6, де
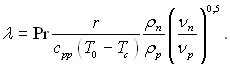
Локальний коефіцієнт тепловіддачі зв’язаний з середнім залежністю:
α| = 2αх=ℓ.
При малих значеннях параметра γ (рис.11.6) формула для локальної тепловіддачі буде:
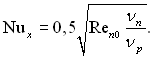 (11.48)
(11.48)
Якщо вважати, що
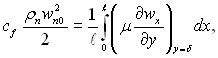
то формула Нуссельта (11.30) можна записати в наступному виді:
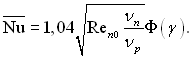
Ця формула з точністю до множника 1,04 співпадає з формулою (11.47).
Підхід до розв’язку задачі про ламінарну плівкову конденсацію як задачі теорії пограничного шару з сильним розривом отримав подальше застосування в роботах багатьох вчених. У цих роботах розглядалася ламінарна плівкова конденсація насиченої пари, що швидко рухається, на плоскій ізотермічній поверхні. Фізичні параметри вважалися усталеними, а швидкість зовнішнього потоку змінюється за степеневим законом. У відповідності з названими умовами задачу можна сформулювати наступним чином.
Конденсат:
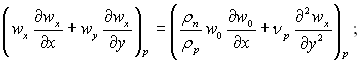 (11.48.1)
(11.48.1)
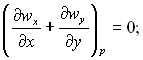 (11.49)
(11.49)
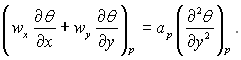 (11.50)
(11.50)
Пара:
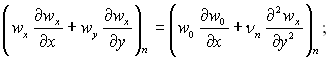 (11.51)
(11.51)
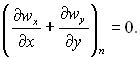 (11.52)
(11.52)
Граничні умови:
![]() (11.53)
(11.53)
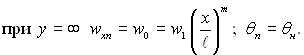 (11.54)
(11.54)
Умови спряження (у = δ):
рівняння збереження маси
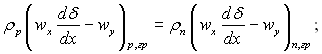 (11.55)
(11.55)
рівність дотичних напруг 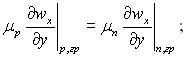 (11.56)
(11.56)
рівняння збереження енергії
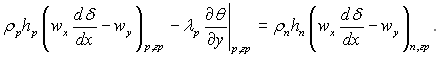 (11.57)
(11.57)
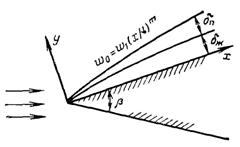
Рис.11.7. Ламінарна плівкова конденсація пари, що швидко рухається, при обтіканні клина (до постановки спряженої крайової задачі)
Формулювання задачі ілюструє рис.11.7. При обтіканні клина тиск у зовнішньому потоці змінюється вздовж потоку, відповідно у зовнішній області змінюється і швидкість w0:
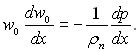
Ця обставина урахована при записі рівняння руху для пари і конденсату. Величина показника т залишається усталеною величиною.
Запишемо умову задачі в безрозмірному вигляді, для чого введемо наступні перемінні:
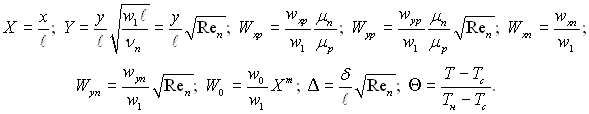
У цьому випадку формулювання задачі набуває наступного вигляду.
Конденсат:
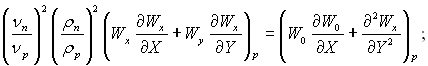 (11.58)
(11.58)
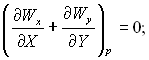 (11.59)
(11.59)
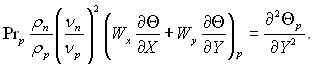 (11.60)
(11.60)
Пара:
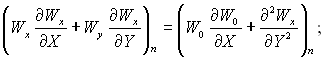 (11.61)
(11.61)
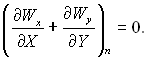 (11.62)
(11.62)
Граничні умови:
![]() (11.63)
(11.63)
![]() (11.64)
(11.64)
Умови спряження (Y = Δ):
рівняння збереження маси 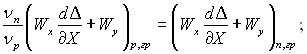 (11.65)
(11.65)
рівність дотичних напруг 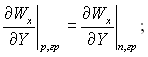 (11.66)
(11.66)
рівняння збереження енергії 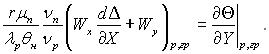 (11.67)
(11.67)
У подальшому використовуємо позначення: