Рівняння з частинними похідними, які входять у формулювання задачі, можна привести до звичайних диференціальних рівнянь, якщо отримати з рівнянь нерозривності (11.59) і (11.62) функції току ψ_р і ψ_п:

(11.68)

(11.69)

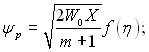(11.70)

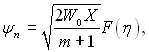(11.71)

де 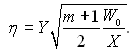(11.72)

Після відповідних перетворень формулювання задачі набуває такого вигляду.

Конденсат: (11.73)

(11.74)

Пара: (11.75)

Граничні умови: (11.76)

(11.77)

(11.78)

(11.79)

(11.80)

Умови спряження: (11.81)

(11.82)

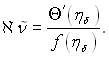(11.83)

Знаком штрих позначено диференціювання по η.

Величина η = η_δ  відповідає поверхні рідина – пара і становить:

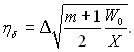(11.84)

У рівняннях позначено також ; С – безрозмірний параметр поперечного потоку маси на поверхні розриву η = η_δ, який підлягає визначенню.

З рівнянь (11.68), (11.76) і (11.82) виходить, що

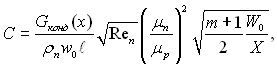
де G_конд витрати конденсату через поперечний переріз плівки δ(х)·1 чи кількість сконденсованої пари за одиницю часу на ділянці пластини х·1; ρ_пw₀ℓ – локальні витрати пари у зовнішній області, які проходять крізь поперечний переріз і рівні ℓ·1; ℓ  – довжина поверхні.

Для пластини, яка обмивається повздовжнім потоком пари, β = 0 і рівняння (11.73) і (11.75) спрощуються. Введемо незалежну змінну ξ = η – η_δ і відповідно замінимо функцію F(η) на F_ξ(ξ). Рівняння (11.75) при цьому залишається незмінним, але штрих позначає диференціювання по ξ. Умови (11.79) і (11.82) заміняються на наступні:

F′_ξ(0) = 0;  F_ξ(0) = 0. (11.85)

Перехід до змінної ξ дозволяє розв’язати рівняння (11.75) незалежно від аналогічного рівняння для конденсату. Цю задачу розв’язано з певними спрощеннями. Вважалося, що у плівці конденсату інерційні сили несуттєві, внаслідок цього рівняння (11.73) приводиться до виду:

f ′′′(η) + β = 0. (11.86)

Також було прийнято, що конвективним теплообміном у плівці, тобто переохолодженням конденсату, можна знехтувати. Цю умову можна тлумачити як припущення, що число Прандтля для рідини мале. У цьому випадку (11.74) перетворюється до наступного виду:

Θ″(η) = 0. (11.87)

Представимо функцію F_ξ(ξ)  у вигляді полінома

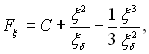(11.88)

де ξ_δ  відповідає зовнішній межі пограничного шару пари.

У рівняння

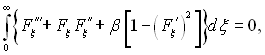
отримане внаслідок інтегрування рівняння (11.75), підставимо значення функції F_ξ  згідно (11.88) і після перетворень, отримаємо:

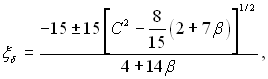(11.89)

де величина ξ_δ  додатна тільки тоді, коли перед квадратною дужкою стоїть знак плюс.

З рівнянь (11.88) і (11.89) що функція F″_ξ(0), яка визначає напругу тертя на поверхні конденсат – пара, має вид:

(11.90)

Визначивши і використавши граничні умови f(0) = 0, можна інтегрувати рівняння (11.86) і (11.87):

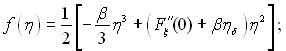(11.91)

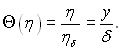(11.92)

Сумісне рішення рівнянь (11.83) і (11.92) дає:

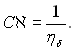(11.93)

З рівнянь (11.83) і (11.89) виходить також, що

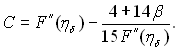(11.94)

Розв’язуючи (11.82) і (11.94) можна отримати:

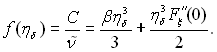(11.95)

Величина визначається чи з рівняння (11.90), чи з рівняння (11.94). З формул (11.94) і (11.95) можна отримати вираз

(11.96)

в якому С визначається згідно рівнянню (11.94).

На підставі сказаного з рівнянь (11.93), (11.94) і (11.96) можна визначити значення [чи ], С і η_δ,, використовуючи наступні параметри:

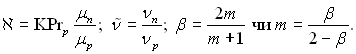
Розраховані значення f ′(η_δ), f ″(η_δ), C і η_δ, які характеризують відповідно швидкість і напругу тертя на між фазній границі, інтенсивність конденсації і товщину плівки, наведені в табл.11.1 як функції

Згідно наведеного розв’язку місцевий коефіцієнт тертя на стінці рівний:

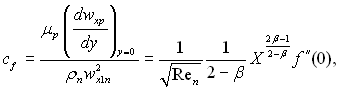(11.97)

а його середнє значення буде

Таблиця 11.1. Значення f ′(η_δ), f ″(η_δ), C і η_δ

Продовження табл. 11.1

а його середнє значення

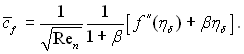(11.98)

Локальне число Нуссельта:

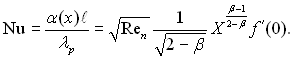(11.99)

Середній коефіцієнт тепловіддачі:

(11.100)

Для плоскої пластини, яка обмивається повздовжнім безградієнтним потоком пари β = 0, формули (11.97)...(11.100) спрощуються.

Як слідує з наведеного рішення, при заданих значеннях параметрів β і ν кількість утвореного конденсату зменшується зі збільшенням א = КPr_p(μ_п/μ_р), зменшується при цьому і коефіцієнт тертя. При інших незмінних умовах збільшенню א відповідає зменшення температурного напору. Але збільшення різниці температур пари і стінки завжди буде зменшувати коефіцієнт тепловіддачі.

Збільшення параметру ν = ν_п/ν_р приводить до зменшення товщини плівки конденсату, що у свою чергу приводить до збільшення коефіцієнта тепловіддачі. При заданих ν і א товщина плівки збільшується зі зменшенням β. В окремому випадку, середня інтенсивність конденсації у точці гальмування потоку (β = 1) менша за швидкість конденсації на плоскій стінці (β = 0).

Можна виділити два граничних випадки, які характеризуються товщиною плівки конденсату. Якщо на пластині (β = 0) плівка дуже тонка, то швидкість її невелика. Наявність плівки не чинить суттєвого впливу на положення границі пари, профіль швидкості пари описується профілем Блазіуса, отриманим при розгляді однорідного пограничного шару. Профілі швидкості і температури у плівці при цьому повинні бути близькі до лінійних.

Якщо плівка рідини достатньо товста, швидкість міжфазної поверхні наближається до швидкості набігаючого потоку пари w₀ і розподіл швидкості у плівці прямує до профілю Блазіуса.

Якщо плівка дуже тонка, то, щоб задовольнити умову рівності дотичних напруг на між фазній поверхні

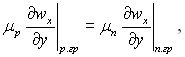
похідна (дw_x/ду)_р,гр. повинна суттєво залежати від відношення ρμ пари і конденсату. Профіль швидкості пари при цьому буде практично не чуттєвим до зміни відношення ρμ.

Навпаки, у випадку товстої плівки, розподіл швидкості близький до розподілу Блазіуса, для задоволення умови рівності дотичних напруг, профіль швидкості пари повинен сильно залежати від відношення ρ_р μ_р / ρ_п μ_п.

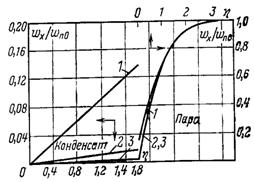
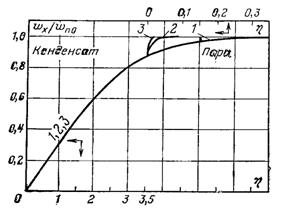
↑ Рис.11.8. Розподіл швидкості в рідині і парі при плівковій ламінарній конденсації

пари, що швидко рухається по пластині η_δ = 1,8; Pr_р = 0,003...100: 1 – (ρ_рμ_р/ρ_пμ_п )^0,5 = 10,                 1/Pr_pK = 0,112…19,6; 2 – (ρ_рμ_р/ρ_пμ_п )^0,5 = 100, 1/Pr_pK = 0,0139…0,0239;3 – (ρ_рμ_р/ρ_пμ_п )^0,5 = 500, 1/Pr_pK = 0,002888…0,00321

Рис.11.9. Розподіл швидкості в рідині і парі при плівковій ламінарній конденсації пари, що швидко рухається по пластині

η_δ = 3,5; Pr_р = 0,003...0,03: 1 – (ρ_рμ_р/ρ_пμ_п )^0,5 = 10,                 1/Pr_pK = 3,08…3,09; 2 – (ρ_рμ_р/ρ_пμ_п )^0,5 = 100, 1/Pr_pK = 3,7…3,12;

Таким чином, відношення ρμ повинно суттєво впливати на розподіл швидкості в тонких плівках і чинити незначний вплив на течію товстих плівок. Останнє ілюструється рис.11.8 і 11.9, де наведено розподіл безрозмірних швидкостей w_x/w₀ у рідині і її парі, отримані Д.Кохом. Він чисельно розв’язав задачу ламінарної плівкової конденсації при β = 0, тобто для випадку повздовжнього обтікання парою плоскої пластини. Враховувався як конвективний теплообмін у плівці, так і сили інерції. Інші умови відповідали раніше розглянутій задачі. Розрахунки виконано для значень (ρ_рμ_р/ρ_пμ_п )^0,5, рівних10, 100 і 500; значення чисел Pr_р становили 0,003; 0,008; 1,0; 10,0; 100,0; відповідно інтервал зміни комплексу КPr_р був достатньо великим.

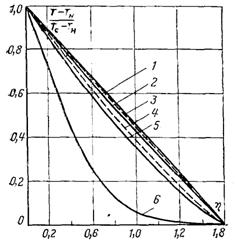
Рис.11.10.. Розподіл температури в рідині при плівковій ламінарній конденсації пари, що швидко рухається по плоскій пластині η_δ = 1,8: 1 – (ρ_рμ_р/ρ_пμ_п )^0,5 = 500, 100, 10 і                  Pr = 0,003…10; 2 – (ρ_рμ_р/ρ_пμ_п )^0,5 = 100,10 і Pr = 1, 10;        3 – (ρ_рμ_р/ρ_пμ_п )^0,5 = 500, Pr = 100; 4 – (ρ_рμ_р/ρ_пμ_п )^0,5 = 10,          Pr = 10; 5 – (ρ_рμ_р/ρ_пμ_п )^0,5 = 100, Pr = 100;                            6 – (ρ_рμ_р/ρ_пμ_п )^0,5 = 10, Pr = 100

На рис.11.10 наведено розподіл температури по товщині плівки. Для рідин з малими числами Прандтля (рідкі метали) температурний профіль практично лінійний. Зі збільшенням числа Прандтля профіль відхиляється від лінійного. Нелінійність температури збільшується також зі зменшенням відношення ρμ, що пояснюється збільшенням ролі конвективного теплообміну.

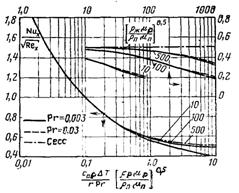
Рис.11.11. Тепловіддача при плівковій ламінарній конденсації пари, що швидко рухається при малих числах Прандтля

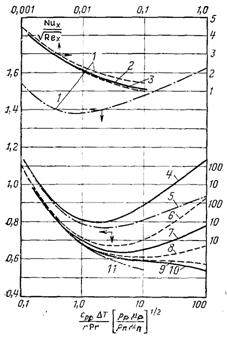
Рис.11.12. Тепловіддача при плівковій ламінарній конденсації пари, що швидко рухається при великих числах Прандтля з показниками відповідно, (ρ_рμ_р/ρ_пμ_п )^0,5,  (Pr): 1 – 10, (100); 2 – 10, 100, (10, 100);    3 – 10, (1), 100, (1, 10), 500, (1, 10, 100); 4 – 100, (100);   5 – 10, (10); 6 – 500, (100); 7 – 100, (10); 8 – 500, (10);    9 – по даним Сесса;10 – 100, (1); 11 – 10, (1)

Результати розрахунку тепловіддачі наведені на рис.11.11 і 11.12. На цих же рисунках наведені дані, отримані аналогічним чином, але без урахування сил інерції і конвективного теплообміну. Для Pr_р = 1 не врахування цих факторів не веде до суттєвих похибок. При великих значеннях числа Прандтля рідини різниця між наближеним і точним рішенням суттєва.

У випадку конденсації порівняно повільного руху пари на вертикальній чи похилій пластині течія і теплообмін можуть суттєво залежати від сили тяжіння. Подібну задачу розв’язував Якобс. Сили інерції конденсату і його переохолодження не враховувалися; приймалося, що ρ_п/ρ_р << 1.

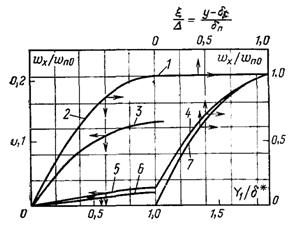
Рис.11.13.Розподіл швидкості у рідині і парі при плівковій ламінарній конденсації рухомої пари фреона-113 у залежності від числа Фруда Fr_x=w²₀/gx, ΔT=22,2 K; δ_p і δ_п – відповідні товщини плівки і пограничного шару пари; Y=(y/x)(Re_x /Fr_x)^0,5; δ*=(δ/x)(Re_x /Fr_x)^0,5; Z=1/Fr:    1 – Z=40,2; 2 – 40,2;      3 – 0,6; 4 – 0,6;                    5 – 6,1·10 ^–3; 6 – 6·10 ^–4; 7 –  6,1·10 ^–3; 6·10

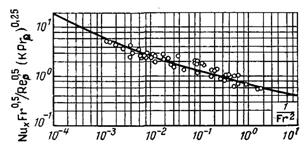
Рис.11.14. Тепловіддача при плівковій ламінарній конденсації рухомої пари фреона-113 у залежності від 1/Fr_x=gx/w²₀. Порівняння розрахункових і дослідних даних Якоба: –––––– – теорія;– дослід

Розподіл безрозмірної швидкості конденсату і пари залежить від числа Фруда Fr_x=w²₀/gx (рис.11.13). При великих числах Фруда профіль швидкості конденсату практично лінійний. При зменшенні Fr епюра швидкості все більше наближається до параболічної, характерній для випадку гравітаційної течії плівки.

У разі, коли число Фруда дуже велике, то

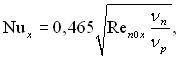
тобто сили тяжіння не актуальні. Результати розрахунку з урахуванням сил тяжіння і тертя наведені на рис.11.14. Розрахунок виконувався для значень 1/КPr_р = 0,00617...0,04319. На цьому ж рисунку наведені дослідні дані, отримані Якобсом при приблизно рівному атмосферному тиску.

Задача про ламінарну плівкову конденсацію пари, що швидко рухається, як задача теорії пограничного шару з сильним розривом досить складна. Ця обставина обумовлює появу наближеного підходу до постановки задачі. Закон тертя на між фазній границі задається згідно рівнянню (11.12), отриманому для випадку сильного відсмоктування. Напруга тертя у цьому випадку вважається обумовленою тільки переносом кількості руху пари під час її конденсації.

Задачу про плівкову ламінарну конденсацію пари, що швидко рухається, за умов прийнятих Нуссельтом, але з урахуванням тертя на межі пара – конденсат, згідно рівнянню (11.12), можна розв’язати при наступному формулюванні: 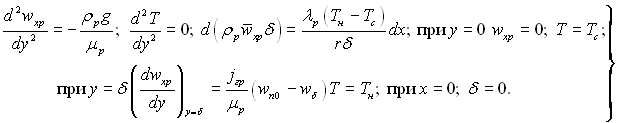(11.101)

Інтегрування рівняння руху з урахуванням назначених граничних умов дає наступний розподіл швидкості по товщині плівки:

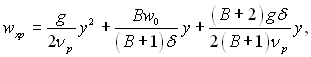(11.102)

де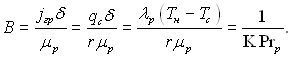

Середня швидкість у перерізі х:

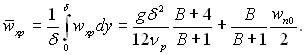(11.103)

При w_n0 = 0 рівняння (11.102) і (11.103) переходять у вирази, отримані Нуссельтом для нерухомої пари за умови, що (dw_xp/dy)_y=δ = 0. Якщо g = 0, розподіл швидкості лінійний.

Підставляючи значення w(_x згідно (11.103) в рівняння

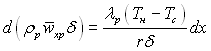
і враховуючи, що_δ (0) = 0, отримаємо після інтегрування рівняння

де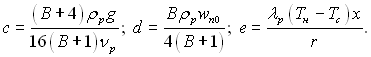

Звідси виходить, що

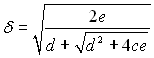(11.104)

і (11.105)

де 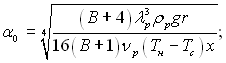(11.106)

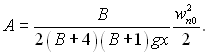(11.107)

При w_n0 = 0 (A = 0) і КPr_p > 10 з похибкою, яка не перевищує 2%, коефіцієнт тепловіддачі α₀ дорівнює отриманому Нуссельтом [див. формулу (10.12)]. Розходження рішень обумовлено прийнятою Нуссельтом умовою на поверхні плівки (dw_x/dy)_y=δ = 0. Якщо KPr_p > 10, можна приймати, що (В + 4) ≈ 4 і (В + 1) ≈ 1. Тоді з (11.105) можна отримати наступну формулу для середньої тепловіддачі на пластині висотою Н:

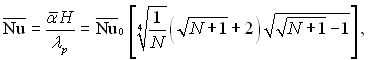(11.108)

де

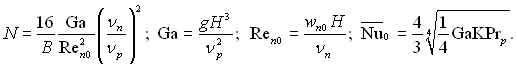
Число відповідає випадку w_n0 = 0 – див. рівняння (10.14).

Умовою практичної незалежності місцевого коефіцієнта тепловіддачі від швидкості пари може служити нерівність:

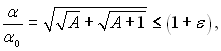(11.109)

де ε  <<1. Для випадку ε  = 0,05 отримуємо, наприклад, що при конденсації водяної пари при атмосферному тиску і Т_н – Т_с = 10 К місцевий коефіцієнт тепловіддачі у перерізі х = 1 м практично не відрізняється від α при конденсації нерухомої пари, якщо швидкість її менше 10 м/с.

Якщо прийняти, що g = 0 (наприклад горизонтально розміщена пластина –див. рис.11.5), то

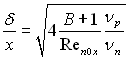і 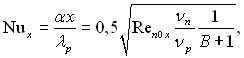(11.110),(11.111)

де

Для плівкової конденсації пари неметалевих речовин величина В у більшості випадків мала у порівнянні з одиницею. Тоді

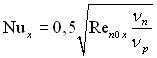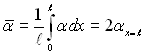чи і 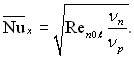(11.112),(11.113)

Розглянуті у цьому розділі рішення отримані без урахування хвильового руху плівки і без урахування можливого зриву конденсату при великих швидкостях. Дослідних даних, отриманих за умов достатньо повної відповідності граничним умовам, прийнятим при розв’язку задач, до цього часу практично не отримано. Ця обставина ускладнює апробацію приведених нами теоретичних результатів.

Ламінарний рух плівки конденсату має місце при числах Рейнольдса рідини в межах від 100 до 500. Якщо використати дані про критичну величину числа Рейнольдса (~2000) для течії однофазної рідини в трубі і врахувати, що еквівалентний діаметр плоскої плівки дорівнює d_e = 4δ, то порядок величини Re_р,кр повинен становити 500. У деяких випадках спостерігалася ламінарна течія при Re_р ≥ 500.

Безпосередньо можна оцінити Re_р,кр плівки шляхом порівняння дослідних даних по теплообміну з даними розрахунків за формулами для тепловіддачі при ламінарній і турбулентній течіях. У турбулентному потоці густина теплового потоку у нормальному напрямку до поверхні стінки, і дотична напруга у певному перерізі, паралельному стінці, можуть виражатися рівняннями (10.60) і (10.61)

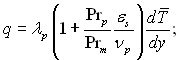
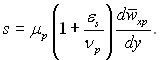(10.60), (10.61)

З рівняння (10.60) виходить, що під час конденсації насиченої пари і R_ф=0

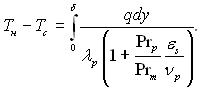(11.114)

Нехтуючи теплотою переохолодження конденсату і вважаючи, що у плівці відсутнє виділення теплоти за рахунок дисипації механічної енергії і внутрішніх джерел, можна написати, що дq_y/ду = 0 чи q = q_c = const. Ураховуючи цю умову, рівняння (11.114) можна записати так:

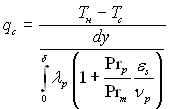чи 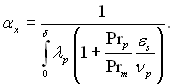(11.115), (11.116)

При певних умовах аналогію процесу перенесення теплоти і кількості руху в турбулентному потоці можна представити наступним чином: 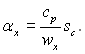Використовуючи для опису розподілу осередненої швидкості логарифмічний закон, матимемо

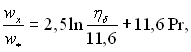
для місцевого коефіцієнта тепловіддачі можна написати:

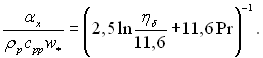(11.117)

У цьому рівнянні w_* = (s_c/ρ_p)^0,5 – динамічна швидкість;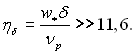

При запису (11.117) вважалося, що плівка тече, затягуючись тертям пари, тоді:

і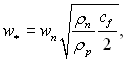

де с_f – коефіцієнт тертя на межі між фазами пара – рідина.