11.3. Зрив конденсату

При взаємодії потоків рідин різної густини на поверхні розділу виникають хвилі. На це явище накладається тертя, яке приводить до прискорення рідини потоком пари при їх паралельному супутньому русі, а при зустрічній течії – до сповільнення, а далі до зворотної течії. При досягненні певної швидкості розпочинається зрив і винесення рідини потоком газу чи пари. Краплі рідини зриваються з гребенів і прямують з потоком газу чи осідають на плівці. Якщо конденсат займає значну частину прохідного перерізу для випадку конденсації в трубі, а швидкість пари ще велика, можливе утворення з наступним рідких пробок.

Рис.11.15. Хвиле утворення і зрив крапель при обмиванні плівки рідини парою, що швидко рухається

Втрата стійкості з наступним винесенням рідини з поверхні плівки пов’язані із взаємодією сил інерції, тяжіння, поверхневого натягу і тертя. Подразнення поверхні розділу виявляються методами гідродинаміки ідеальної рідини, тобто без урахування сил в’язкості і поверхневого натягу. Названі сиди відповідним чином трансформують процес.

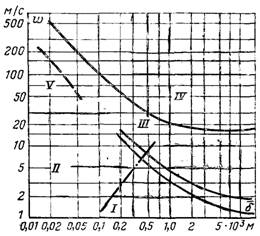
Рис.11.16. Залежність режимів течії плівки від швидкості газу при Т = 293 К: І – гладка поверхня; ІІ – повільні хвилі; ІІІ – тримірні і двомірні хвилі; ІV – відрив і руйнування плівки; V – неповне змочування

На рис.11.16 наведені дані Вурца, які виявляють границі різних режимів руху плівки води на плоскій поверхні, що обмивається повздовжнім потоком газу.

При малих швидкостях газу і малій товщині плівки спостерігається спокійна течія з гладкою поверхнею чи повільними хвилями малої амплітуди (області І і ІІ). Зі збільшенням швидкості і товщини плівки спочатку спостерігається перехід до хвильового руху (ІІІ), а в подальшому відрив і руйнування плівки (IV). При великій швидкості газу і дуже тонкій плівці може виникнути розрив плівки на окремі струминки чи краплі (V), що залежить від параметрів змочування.

Згідно з даними С.С.Кутателадзе стабільність структури двофазного потоку визначається стійкістю елементів, які його утворюють. Фактором, руйнуючим такий елемент, є динамічний напір фази, що його обмиває, а стабілізуючим фактором – тиск, обумовлений поверхневим натягом. Мірою відношення цих сил служить число стійкості:

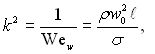(11.118)

де – динамічний напір фази, яка обмиває розглядуване утворення іншої фази; ℓ – характерний розмір цього утворення.

Коли можна вважати, що

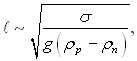
то число стійкості k набуває вигляду:

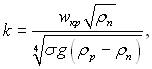(11.119)

де w_кр – швидкість руху парової фази, за якої починається втрата стійкості.

Якщо на границі розділу фаз має місце хвиле утворення, то число (11.118) може тлумачитися як відношення кінетичної і потенціальної енергії хвильового руху до зміни енергії хвилі, обумовленому поверхневим натягом. Нестійкість границі розділу фаз, викликану порушенням необхідного співвідношення цих сил, називають нестійкістю Тейлора.

У механізмі нестійкості, розглянутим Гельмгольцем і Релеєм, число (11.118) оказується слабкою функцією відносної густини фаз:

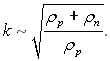
Нижче наводяться залежності, запропоновані для визначення числа стійкості.

Початок видимого зриву крапель при зустрічній течії рідини і газу відповідає рівнянню:

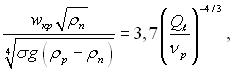(11.120)

де Qℓ – об’ємні витрати на 1 м довжини змочуваної поверхні, м³/(м·с).

Початок зриву при паралельно струминній горизонтальній течії плівки і газу спостерігається при:

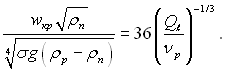(11.121)

Початок зриву рідини при паралельно струминній супутній течії зверху вниз плівки і газу відповідає рівнянню:

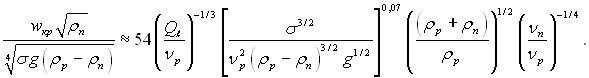(11.122)

Частина рідкої плівки зберігається на стінці навіть при швидкості газу, який значно перевищує швидкість звуку. Під час конденсації потоншення плівки, викликане хвиле утворенням з наступним зривом, повинно приводити до місцевого зростання інтенсивності теплообміну, якщо основним термічним опором є опір плівки. Коефіцієнти тепловіддачі повинні зростати, а товщина плівки повинна поновлюватися.

Експериментальні дослідження зриву води односпрямованим паровим потоком, що тече у трубі d = 25 мм в ізотермічних умовах, дали можливість для критичної швидкості пари, за якої настає зрив рідини з поверхні плівки, отримати наступне рівняння

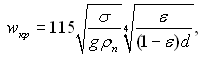
яке можна представити в іншому виді:

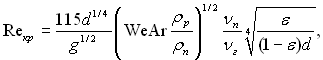(11.123)

де 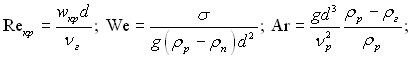w_кр – критична швидкість газу; ε – масовий витратний паровміст суміші; індекси “р” і “г” стосуються відповідно рідини і газу; 115 – розмірний коефіцієнт, м^1/4с^–1.

З формули (11.123) виходить, що при інших незмінних умовах, ріст паровмісту призводить до зменшення критичної швидкості.

Крапельне винесення рідини з плівки, які турбулентно рухаються у вертикальній трубі, теоретично розглянуті за наступних умов: рух плівки і газу вважається симетричним відносно осі; крапельне винесення залежить від структури і інтенсивності пульсуючого руху рідини; течія ізотермічна.

Розгляд стійкості течії приводить до рівняння, яке пов’язує між собою турбулентні напруги і стан поверхні плівки, нерівності якої характеризуються пульсацій ними векторами х′ w′ і п′:

(11.124)

де w′_x, w′_r – відповідно повздовжня і радіальна складові пульсаційної швидкості рідини; δ – товщина плівки; σ – поверхневий натяг; ε_с – відстань від стінки, що відповідає умові рівності повздовжньої складової швидкості w_x і швидкості розповсюдження подразнень (позначається індексом “с”); п′ – напрямок нормалі до миттєвої поверхні плівки; f – деяка функція, яка незначно відрізняється від одиниці.

З рівняння (11.124) виходить, що при зменшенні ε_с нерівності вільної поверхні, а значить і ймовірність розпаду плівки зростає. Найменше значення ε_с  відповідає товщині в’язкого підшару.

Інтенсивність турбулентного розпаду плівки визначається в основному кількістю питомої енергії пульсацій швидкості. Це зв’язано з тим, що повна зміна турбулентних напруг за перерізом плівки повинна дорівнювати нулю, напруга на вільній поверхні повинна компенсуватися тільки силами поверхневого натягу.

Винесення рідини призводить до зменшення товщини плівки і, як наслідок, до зменшення її термічного опору, якщо властивості переносу залишаються незмінними. Зміну товщини плівки можна описати рівнянням виду:

δ = δ₀ехр(– const·х),

де δ₀ – початкова товщина плівки; х – повздовжня координата.

На рис.11.17 і 11.18 наведено опрацювання дослідних даних Чена і Ібеле для конкретних умов двофазної течії рідини і газу.

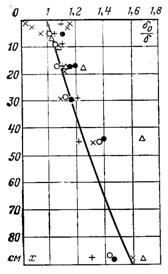
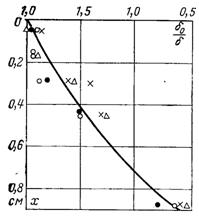
↑ Рис.11.17 Залежність δ₀/δ = ехр (0,512х·10^–2);Re_г =6,6·10 ⁴: ¡ – G_p= 38,2; l – 27,2;  r – 17,7; Π– 9,65; Ç – 2,9 г/(см·с)  

Рис.11.18 Залежність δ₀/δ = ехр (0,975х·10^–2);Re_г =2,6·10 ⁵. Умовні позначення на рис.11.17  ↑

Розвиток хвиль і зрив рідини досліджені в основному при обмиванні рідкої фази іншої фізичної природи, тобто без конденсації і в ізотермічних умовах. У випадку конденсації поперечний потік пари змінює гідродинамічну обстановку в області біля міжфазної границі. Необхідні спеціальні дослідження, які дозволили б провірити придатність даних, отриманих в ізотермічних умовах, до умов течії плівки при конденсації пари, що швидко рухається.

Деякі побічні підтвердження можливості використання формули (11.123) для випадку конденсації випливають з дослідження тепловіддачі при конденсації пари у вертикальній трубі з входом пари зверху. При великих локальних числах Рейнольдса плівки і пари отримано різке збільшення коефіцієнта тепловіддачі α_х на окремих ділянках (“сплески”). Можна вважати, що різке збільшення місцевого коефіцієнта тепловіддачі обумовлено зривом плівки.

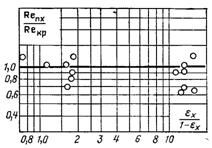
Рис.11.19.Порівняння дослідних даних з результатом розрахунку по формулі (11.14)

Було виконано співставлення значень чисел Рейнольдса парового потоку в перерізах, попередніх до “сплеску” зі значеннями Re_кр визначеними по формулі (11.123). Порівняння наведено на рис.11.19. Тут ε_х – витратний масовий паровміст в перерізі з координатою х, яка відраховується від початку поверхні конденсату. Відношення Re_пх/Re_кр відрізняється від одиниці не більше чим на 35%.

У перерізах передуючих “сплеску” α_х, числа Рейнольдса становили для пари (2...6)10⁴, для плівки 32...500, діаметр труби був 10 мм, тиск пари складав 0,1...0,6 МПа.

Зірвані краплі можуть нерівномірно розподілятися по перерізу парового потоку. Нерівномірність розподілу обумовлена як процесом зриву, так і процесами, які стосуються сукупності крапель, що рухаються в парі.

Краплі рухаються з парою, яка їх затягує. До них прикладена рівнодіюча сила лобового опору, яка залежить від режиму обмивання і форми крапель. Має місце ковзання, яке проявляється в різниці повздовжньої швидкості крапель і середньої витратної швидкості пари. Прискорення краплі приводить до ефекту “приєднаної маси”. Під час руху в неоднорідному полі повздовжньої складової швидкості пари краплі набувають обертовий рух, з’являється підйомна сила (ефект Магнуса) – з боку краплі, де складова швидкості обертання і поступальної швидкості додаються, тиск менший.

Малі краплі, розмір яких набагато менший масштабу турбулентності, можуть переміщуватися під дією турбулентної дифузії. У сукупності дуже дрібних крапель проявляється дія броунівського руху. Для крупних крапель може бути актуальна і сила тяжіння.

Краплі можуть мати температуру меншу температури фазового переходу. В наслідок цього додатково відбувається конденсація пари на краплях, проявляються реактивні сили. Крім цього, зірвані краплі знаходяться в поперечному потоці пари, яка рухається по напрямку до холодної стінки.

У залежності від конкретних умов усі ці фактори можуть проявлятися по-різному.

Зірвані краплі мають різні розміри і, як наслідок, різні швидкості. Крупні краплі рухаються вздовж потоку повільніше. Краплі мають і бокове зміщення, при цьому швидкість цього зміщення залежить від розміру крапель. Внаслідок сказаного, розподіл крапель за розмірами може змінюватися в об’ємі пари.

При зштовхуванні краплі можуть об’єднуватися чи відскакувати. Останнє мабуть більш ймовірне для дрібних крапель. Коагуляція може привести до утворення краплі такого великого розміру, що вона знову розпадеться на більш дрібні.

Таким чином, процес руху ансамблю крапель дуже складний. Вивчення руху крапель може стати предметом самостійного дослідження.

Для характеристики двофазних течій представляє інтерес функція розподілу крапель, що зірвалися з плівки, за розмірами. Для розподілу крапель по об’ємам запропонована формула:

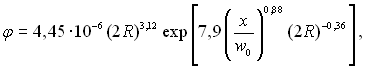(11.125)

де φ = V(R)/V – функція розподілу; V(R) – об’єм крапель з радіусом (R); V – загальний об’єм крапель; R – радіус сферичної краплі; w₀ – характерна швидкість.

Функція розподілу (11.125) погоджується з дослідними даними Х.Якоба для частинок з радіусами менше 0,1 мм.

У випадку зриву крапель з поверхні плівки паровий пограничний шар містить дві фази: пара і краплі рідини. Краплі, які потрапляють в пограничний шар, прискорюються завдяки пари. Пара ж гальмується, віддаючи краплям певну кількість руху. Характеристики двофазного пограничного шару змінюються в порівнянні з однофазним, але повинні залежати від відміченого раніше руху крапель в пристінній області. Двофазний пограничний шар вивчений порівнянно мало.

11.4. Конденсація в трубі

У трубі паровий об’єм обмежений стінками, що приводить до спрямованого руху пари. В інтенсивно охолоджувальних довгих трубах швидкість пари на вході може досягати дуже великих значень. Впливаючи на теплообмін, вона в той же час залежить від нього. Швидкість пари зменшується по довжині труби і при повній конденсації пари в кінцевому перерізі дорівнює нулю. За певних умов кінцева частина труби може бути заповнена конденсатом.

Конденсат і пара можуть рухатися як ламінарно, так і турбулентно. На вході в довгу трубу течія пари може бути турбулентною. По мірі конденсації пари її швидкість зменшується і турбулентна течія може перейти в ламінарну. Одночасно вздовж труби може безперервно збільшуватися витрата конденсату, і його течія з ламінарної може перейти в турбулентну.

При певних умовах має місце хвиле утворення і зрив конденсату. Течія і теплообмін можуть залежати від взаємного напрямку, значення сил тяжіння і тертя і від інших факторів.

Сполучення перелічених умов робить задачу про теплообмін при конденсації пари в трубі складною і затрудняє строге і повне рішення. Ускладнюється і аналіз результатів експерименту, особливо коли вимірюється тільки середня в трубі тепловіддача. Неможливість розпізнавання окремих режимів, реалізованих при експерименті, часто веде до того, що отримані результати придатні тільки для опису тотожних процесів. Тому головною задачею при проведенні дослідів і їх аналізі є розділення процесу на окремі, порівнянно елементарні процеси, які підлягають опису. При цьому можна використати рішення, отримані для простіших задач, і на їх основі виконувати аналіз загальної картини.

У техніці при конденсації пари у вертикальних трубах зазвичай віддається перевага впуску пари зверху. Напрямок сил тяжіння і тертя при цьому співпадають, що сприяє збільшенню тепловіддачі до внутрішньої поверхні труби.

Ламінарна течія плівки. Розглянемо наближений розв’язок задачі. Вважаємо, що насичена пара рухається зверху вниз у трубі з круглим поперечним перерізом. Фізичні параметри пари і конденсату постійні. Температури поверхні плівки і стінки відповідно дорівнюють Т_н і Т_с. Нехай температура по товщині плівки змінюється за лінійним законом, тоді

(11.126)

Це рівняння рівнозначне нехтуванню теплотою переохолодження (конвективним теплообміном), теплотою тертя і циліндричністю шарів конденсату. Для тонких шарів останнє уявлення не викликає серйозних заперечень.

Товщина плівки визначається рівнянням:

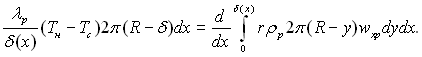(11.127)

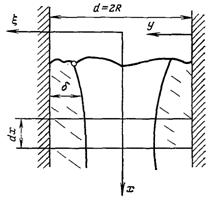
Рис.11.20. До постановки задачі про ламінарну плівкову конденсацію у вертикальній трубі

Ліва частина визначає тепловий потік dQ, Вт, на елементі плівки довжиною dx. Права частина визначає ту ж величину як прирощення витрат dG, кг/с на елементі дх, помножене на теплоту фазового переходу r, Дж/кг. Величина R – y представляє собою поточний радіус кільцевого шару конденсату, який змінюється від R до R – δ (рис.11.20), де R – радіус труби.

Розподіл швидкості у плівці описується рівнянням:

w_xp = a + by + cy² + dy³. (11.128)

Значення a, b, c і d визначаються, виходячи з граничних умов:

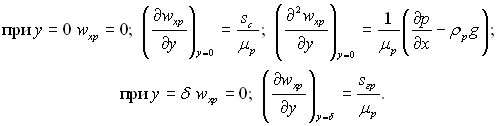(11.129)

Зміну тиску по довжині труби опишемо рівнянням

(11.130)

При великих значеннях чисел Рейнольдса (турбулентна течія) для визначення коефіцієнта опору тертя приймаємо формулу Кармана:

ζ =0,184Re_d^–0,2. (11.131)

Значення w(_n можна визначити з рівняння нерозривності парового потоку, згідно якому масові витрати пари в довільному перерізі дорівнюють початковим витратам (на вході в трубу) за мінусом сконденсованої пари. Тоді

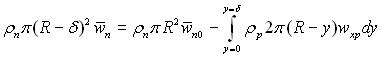
чи

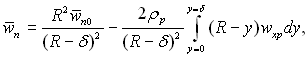(11.132)

де w(_n0 – середня швидкість пари на вході в трубу.

Оскільки товщина плівки конденсату δ змінюється по довжині труби, необхідно добавити початкову умову. Нехай

при х = 0 δ(0) = 0. (11.133)

Рівняння (11.126)...(11.133) складають математичне формулювання задачі, яка розв’язана Х.Хартманом числовим методом при зміні основних параметрів у межах:

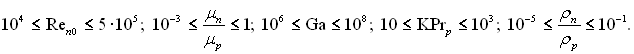
Згідно розрахунку за цих умов вплив сили тяжіння практично не проявляється і число Галілея можна не враховувати. При цьому s_c= s_гр = c_f(ρ_nw_n²/2), тобто напруга тертя не змінюється по товщині плівки конденсату.

Результати розрахунку середнього коефіцієнта тепловіддачі при повній конденсації пари апроксимовані наступним степеневим рівнянням:

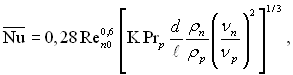(11.134)

де 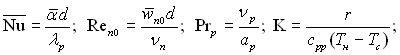d – внутрішній діаметр труби; ℓ – її довжина. Формула (11.134) отримана для Re_n0 ≥ 2,5·10⁴; μ_п/μ_р ≥ 0,1; ρ_п/ρ_р ≤ 10^–3.

Для Re_n0 > 10⁵, як показують розрахунки, числа Re_р = w(_хрÑ_хрδ_р вже недалеко від входу в трубу перевищує критичне значення, при якому ламінарний рух плівки переходить у турбулентний. У розглядуваних дослідженнях критичне число Рейнольдса плівки приймалося рівним 60.

Співставлення формули (11.134) з дослідними даними, які проведені при конденсації насиченої водяної пари з тиском, приблизно рівним атмосферному, в мідній вертикальній трубі діаметром d = 10 мм і довжиною ℓ  =1026 мм. Числа Рейнольдса змінювалися в межах: Re_n0 = 10⁴...5·10⁴; Re_р = 107...540. Інші визначальні безрозмірні величини складали:

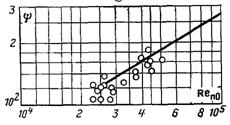
Рис.11.21. Порівняння дослідних даних В.П.Ісаченка по середній тепловіддачі з розрахунком за (11.134)

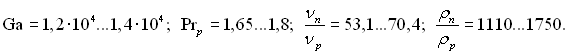
Усі фізичні параметри вибиралися по температурі насичення.

Як видно з рис.11.21, дослідні дані в основному відповідають формулі (11.134). На цьому рисунку:

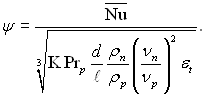
Для урахування змінності фізичних параметрів конденсату в рівняння (11.134) в першому наближенні вводиться поправочний множник

де числа Прандтля конденсату вибираються відповідно за температурою насичення і стінки.

Апроксимація Хартманом тільки середніх коефіцієнтів тепловіддачі є певним недоліком роботи, тому що затрудняє перевірку формули (11.134). В дослідах можливе співіснування різних режимів течії пари і конденсату, при цьому їх межі не завжди можна чітко визначити. При повній конденсації число Рейнольдса пари повинно зменшуватися вздовж труби. У вихідному перерізі повздовжня швидкість пари відсутня Можна вважати, що в кінцевій частині труби пара буде рухатися ламінарно, що входить у протиріччя з математичним формулюванням задачі.

У дослідах під керівництвом В.П.Ісаченка вивчалася місцева тепловіддача при конденсації водяної пари з тиском, приблизно рівним атмосферному (Т_н = 99,6...100,7 °С), в латунній трубі з внутрішнім діаметром 10 мм, і зовнішнім – 80 мм. Довжина труби була ℓ = 390 мм, що робило більш ймовірним отримання ламінарного режиму течії плівки конденсату. У дослідах відбувалася повна конденсація всієї пари, що надходила в трубу, утворений конденсат вільно зливався з труби до приймального пристрою. Таким чином, у вихідному (нижньому) перерізі труби витратна швидкість пари практично дорівнювала нулю.

За отриманими дослідними даними розраховувалася середня тепловіддача на порівнянно короткій ділянці труби Δх = х₂ – х₁ (координата х відраховувалася від вхідного перерізу труби, де починалася конденсація пари). Дані про розміри ділянок і їх розміщення наводяться нижче.

Номер ділянки 1 2 3 4 5 6 7 8 9 10

х₁, мм 0 0 0 146 196 246 146 146 196 0

х₂, мм 146 196 246 390 390 390 340 290 340 390

Числа Рейнольдса плівки і пари і число Фруда, віднесені до середини ділянки х( = 0,5(х₁ + х₂), змінювалися в таких межах Re_px( = q|_cx|/rμ_p = 19,7…206; Re_nd = w|_nx| d/ν_n = 1800…17000; Fr(ρ_n/ρ_p) = (w|_nx|  ²/gх| )(ρ_n/ρ_p) = (0,26…98)·10^–2; при цьому w|_nx|  = 3,6...33,5 м/с; середній на ділянці температурний напір становив    θ_x|  =8,1...60,4 °С.

На кінцевих ділянках труби (ділянки 4, 5, 6) швидкість пари порівняно невелика в межах 6 м/с. Тут можна очікувати відсутність впливу швидкості пари на теплообмін. Щоб для порівняння з формулами для нерухомої пари врахувати початкову товщину плівки, не рівну нулю при всіх х₁> 0, співставлення дослідних даних виконувалося за середньою тепловіддачею, яка визначалася по формулі (10.58) для розрахункової ділянки х₂ – х₁:

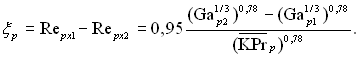(11.135)

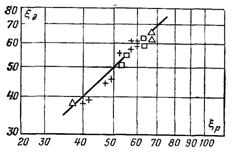
Рис.11.22. Порівняння дослідних даних з розрахунками по (11.135):r – ділянка 4; * – ділянка 5; З – ділянка 6

Порівняння розрахованої по формулі (11.135) тепловіддачі з дослідними значеннями ξ_д = q(_cx( (х₂ – х₁)/r_p наведено на рис.11.22. Згідно розрахункових і дослідних даних можна вважати, що на нижніх ділянках труби, для яких виконано порівняння, мав місце ламінарний режим стікання плівки. Отже, у даному випадку у всій трубі плівка тече ламінарно.

Для випадку конденсації пари на вертикальній стінці і течії конденсату і пари зверху вниз було отримано рівняння (11.25)

(11.25)

в якому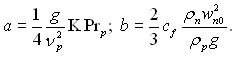

Вважаючи, що α_х = λ_р/δ_р(х), рівняння (11.25) можна записати в наступному виді:

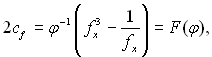(11.136)

де f_x = α_x/α_0x  – відносний місцевий коефіцієнт тепловіддачі; α_0x – місцевий коефіцієнт тепловіддачі при конденсації нерухомої пари;

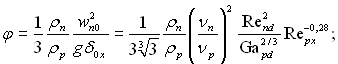(11.137)

δ_0х  – товщина плівки в перерізі х при конденсації нерухомої пари.

Приймаючи, що f_x = с_f (2/k), де k – деяка безрозмірна величина, яку необхідно визначити. Внаслідок цього з (11.136) отримаємо:

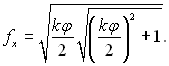(11.138)

Введення величини k не вимагає попередньої інформації про особливості визначення коефіцієнта тертя на границі розділу пара – рідина, k підбирається на підставі експерименту. У загальному випадку величина k може бути функцією від φ.

З урахуванням зроблених зауважень представляється можливим використати в першому наближенні функції виду (11.138) для опису теплообміну на невеликих ділянках труби. На таких ділянках швидкість пари суттєво не змінюється. У подальшому замінимо kφ на k₁φ₁, де

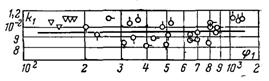
Рис.11.23. Залежність k = k₁φ₁ для ділянок 1...3 і 8

Залежність k₁ = k₁(φ₁) наведена на рис.11.23. Для більш точного визначення k₁ використані дослідні дані, для яких f_x ≥ 1,5. З цих даних виходить, що k₁ ≈ 0,01. Похибка при визначенні f_x за рівнянням (11.138), пов’язана з неточним вибором значення  k, яке при зменшенні  f_x повинно також зменшуватися. Формула (11.138) відповідає граничному переходу до нерухомої пари. При φ → 0 (w_n→0) і кінцевих значеннях k згідно (11.138) f_x → 1.

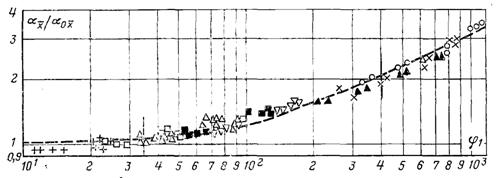
Рис.11.24. Залежність середнього відносного коефіцієнта тепловіддачі від φ₁: для ділянок Ў – 1;Н – 2; p – 3;r – 4; Ј – 5; Ж – 6; ў – 7;s – 8

На рис.11.24 дослідні дані для всіх ділянок, розміри яких наведені вище, подані у вигляді залежності . Суцільною лінією показані значення, які відповідають розрахованим по формулі (10.58) для нерухомої пари. Пунктирна крива відповідає формулі

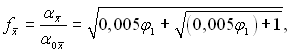(11.139)

де φ визначається згідно з виразом (11.137), але з підстановкою середніх на розрахунковій ділянці величин [віднесених до х = 0,5(х₁ + х₂)]. У першому наближені коефіцієнти тепловіддачі, які відповідають формулі (11.139), можна вважати місцевими.

При φ ≤ 35 тепловіддача практично не залежить від швидкості пари (f_x≈ 1). При φ ≥ 400  дослідні дані наведені на рис.11.24, можна апроксимувати рівнянням виду:

З порівняння цього рівняння з рівнянням для нерухомої пари

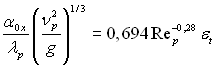
виходить, що у розглядуваних дослідженнях при φ₁ ≥ 400 ламінарна плівка тече в основному під дією сил міжфазного тертя, що діє з боку пари. Дослідними даним наведеним на рис.11.24 при φ₁ ≤ 35 відповідає умова Re_nd < 3·10³, при    φ₁ ≥ 400  умова буде Re_nd > 10⁴. Таким чином, в умовах проведених досліджень міжфазне тертя пов’язане з режимом течії пари, так само як значення Re_nd, що становлять приблизно 3·10³ і 10⁴, і є граничними значеннями для перехідної області течії. При наявності відсмоктування пари (конденсату) повинно мати місце збільшення критичного числа Рейнольдса.

Опис середньої тепловіддачі на порівнянно довгих ділянках (0, х), ускладнюється у зв'язку з тим, що на них може мати місце одночасного існування різних режимів руху. У залежності від конкретного сполучення по довжині труби різних режимів течії плівки і пари можна чекати різних значень середніх коефіцієнтів тепловіддачі при різних умовах роботи теплообмінників і, що особливо важливо, можуть мати місце різні залежності середньої тепловіддачі від основних впливаючих факторів.

Розглянемо конденсацію пари при турбулентній течії плівки з переважним впливом швидкості пари. У цьому випадку орієнтація труби у просторі не має значення, тому що сили тяжіння дуже малі у порівнянні з силами міжфазного тертя. Використовуючи аналогію між переносом теплоти і кількістю руху при течії в трубі, в найпростішому випадку можна написати вираз для напруги тертя на стінці:

(11.140)

де ζ – коефіцієнт гідравлічного опору.

Вважаємо, що цей вираз можна застосувати і для визначення напруги тертя на поверхні розділу пара – рідина при кільцевій течії плівки у довгій трубі. Введемо замість середньої швидкості пари деяку еквівалентну швидкість рідини w_e.n, яка створює таку саму напругу тертя на між фазній поверхні, що і потік пари. Тоді

(11.141)

Підставляючи у вираз аналогії Рейнольдса

значення швидкості згідно рівнянню (11.141), отримаємо:

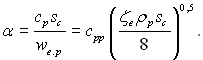(11.142)

У подальшому необхідно оцінити значення величин ζ_е і s_c. Вважаємо, що в ядрі потоку тече парорідинна емульсія. Для неї за аналогією з попереднім запишемо:

(11.143)

де індексом “см” позначаються величини, які стосуються парорідинної суміші. Вважаємо, що витрати у плівці G_p набагато менші витрат суміші G_см, що дозволяє вважати витрати суміші приблизно рівними витратам G_ц, які відповідають швидкості циркуляції w_ц (при повному заповненні труби рідиною):

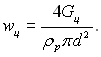
Умова G_p << G_см передбачає інтенсивний зрив конденсату з поверхні плівки. Тоді

і

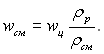
Швидкість циркуляції w_ц зазвичай задається чи може бути розрахована. Підставляючи значення w_см згідно останнього рівняння у формулу (11.143), отримаємо:

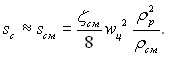(11.144)

Якщо рідина заповнює всю трубу, що при конденсації може мати місце у кінці довгої труби, то

і

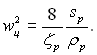
Дані для визначення ζ_р і s_р, як правило, відомі. Підставляючи значення w_ц² у формулу (11.144), матимемо:

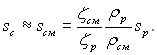
З урахуванням останнього рівняння з (11.142) отримуємо:

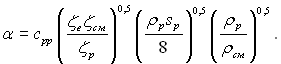(11.145)

Коефіцієнти ζ_е і ζ_см не можуть зараз визначатися з достатньою точністю. Якщо прийняти, що  ζ_е = ζ_см = ζ_р, то попереднє рівняння можна записати так:

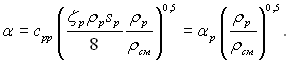(11.146)

Величина α_р може визначатися за відомими рівняннями для коефіцієнта тепловіддачі турбулентній течії рідини в довгій трубі, наприклад по формулі

(11.147)

У першому наближені можна вважати, що ця формула дає і локальні значення коефіцієнта тепловіддачі (довгі труби, слабка змінність фізичних властивостей рідини і граничних теплових умов та ін.). Відношення густин ρ_р/ρ_см можна виразити через витратний паровміст х = G_n/G_см:

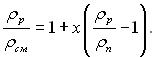
У результаті після підстановки значень 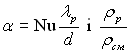в (11.146) для локального коефіцієнта тепловіддачі була запропонована формула

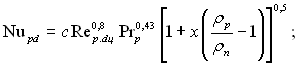(11.148)

а для середнього

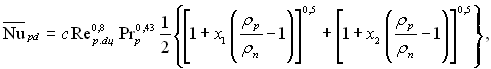(11.149)

де х₂ і х₂ – відповідно паровміст на вході і на виході з труби.

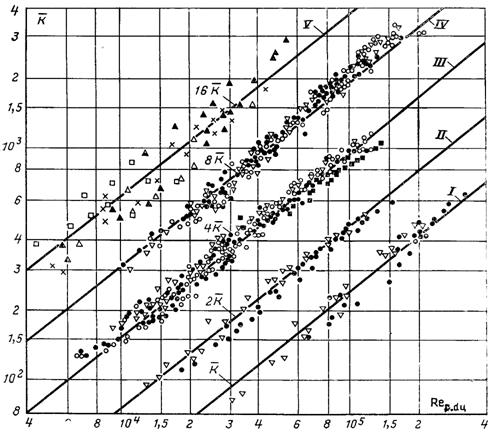
Рис.11.25. Тепловіддача при конденсації водяної пари в трубі за умови турбулентної течії конденсату, де

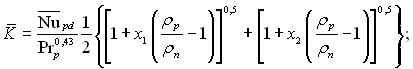суцільні лінії – розрахунок по формулі (11.149), І, ІІ, ІІІ, ІV – дані Л.Д.Бойко, р=0,123...8,8 МПа, горизонтальні труби: І – 1₁<0, 1₂<0; II – 1₁<0, x₂=0; III – x₁=1, x₂=0; IV – x₁=1,1>x₂>0; ℓ=2000 мм, d=16 мм; s–ℓ=2500 мм, d=20 мм; ¡–ℓ=2500 мм, d=13 мм;n–ℓ=11954 мм, d=16 мм;V – дані В.В.Корсетова для режимів: x₁=1,1>x₂>0, р=1...8,8 МПа, q=(68…800)10³Вт/м²:¨–ℓ=2000 мм, d=22 мм; r–ℓ=2000 мм, d=13 мм (горизонтальні труби);Í–ℓ=3200 мм, d=13 мм;      p–  2200 мм, d=13 мм; p– 2200 мм, d=13 мм (вертикальні труби)

Формули (11.148) і (11.149) порівнювалися з даними різних авторів. Результати порівняння наведено на рис.11.25. Порівняння показали, що структура формул (11.148) і (11.149) дозволяють апроксимувати дослідні дані для горизонтальних труб при числах Рейнольдса плівки і пари, відповідно більших 200 і 5000. Для випадку конденсації водяної пари у вертикальній трубі при його русі зверху вниз можливість використання формули (11.149) була підтверджена аж до чисел Рейнольдса від 1000 і більше. Коефіцієнт пропорційності отриманий для труб з нержавіючої сталі с = 0,024, для мідних с = 0,032. Надійна погодженість з дослідними даними отримана для латунних труб при с = 0,026. Залежність коефіцієнта пропорційності від матеріалу труб не знайшла повного пояснення. Різниця коефіцієнтів пояснюється впливом макроструктури поверхні труб.

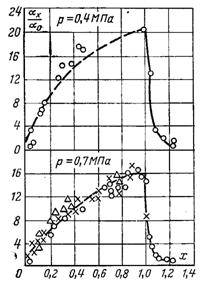
h Рис.11.26. Залежність безрозмірного коефіцієнта тепловіддачі від відносної ентальпії х при конденсації перегрітої пари в трубі при р=0,4 і 0,7 МПа:Ў – d = 2,85; r – 8;Н–10 мм

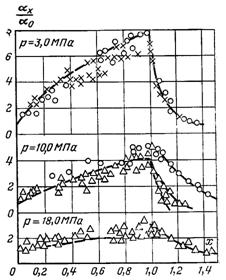
Рис.11.27. Залежність безрозмірного коефіцієнта тепловіддачі від відносної ентальпії х при конденсації перегрітої пари в трубі при р=3; 10 і 18 МПа:Ў – d = 2,85; r – 8;Н–10 ммh

Якщо конденсується перегріта пара, інтенсивність тепловіддачі може змінюватися. Це наглядно видно з рис.11.26 і 11.27. Перегрітій парі відповідають значення відносної ентальпії потоку

більші за одиницю. У цьому рівнянні h_см – питома ентальпія двофазної суміші; h_р – ентальпія рідини на лінії насичення. Штрихова крива відповідає розрахунку за формулою (11.148) величини α_х/α₀, де α₀  – коефіцієнт тепловіддачі, який визначається за формулою (11.147).

При конденсації насиченої пари, тобто при х, що змінюється від 0 до 1, тепловіддача в основному підпорядковується залежності виду (11.148). По мірі росту х теплообмін інтенсифікується. Тепловіддача перегрітої пари тим менша, чим більший х, і прямує до граничного значення, яке відповідає однорідній рідині (парі). Зміна теплообміну в залежності від величини х проявляється найбільш різко при низьких тисках. Різниця все більше зменшується при збільшенні тиску.