ЧАСТИНА ПЕРША ТЕПЛОПРОВІДНІСТЬ

Теплопровідністю називається молекулярний перенос теплоти в суцільному середовищі. Цей процес виникає внаслідок нерівномірного розподілу температур в середовищі. У цьому випадку теплота передається за рахунок безпосереднього контакту між частинками, які мають різну температуру, що веде до обміну енергії між молекулами, атомами чи вільними електронами.

Розділ 1. ТЕОРІЯ ТЕПЛОПРОВІДНОСТІ. ЗАГАЛЬНІ ДАНІ

1.1.Температурне поле, градієнт температури і закон Фур’є

Температурним полем тіла (чи системи тіл)називається сукупність значень температури, яка береться по його об’єму у довільний момент часу. Математично поле температур можна розглядати у вигляді рівняння F

F(t,x,y,z,τ) = 0.

В інженерній практиці приходиться мати справу як з нестаціонарними, так і зі стаціонарними температурними полями. Перше з цих полів змінюється як в просторі, так і в часі, а друге залежить тільки від просторових координат.

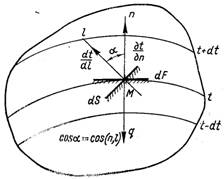
Рис.1.1. До визначення градієнта температур і формулювання закону Фур’є

Зміна температурного поля в просторі спостерігається тільки в напрямках, що пересікають поверхні з однаковою температурою (ізотермічні поверхні); при цьому найбільша зміна має місце в напрямку нормалі до ізотермічної поверхні (рис.1.1).

Границя

(1.1)

називається в теорії теплообміну градієнтом температури, де 1_п – орт (одиничний вектор) нормалі; п – нормаль до ізотермічної поверхні. Градієнт температури представляє собою вектор, спрямований по нормалі до ізотермічної поверхні і чисельно рівний частинній похідній від температури по цьому напрямку. Вважається grad t додатним, якщо він спрямований в бік збільшення температури.

У 1804 р. французький вчений Біо висказав гіпотезу, згідно з якою кількість теплоти, що проходить через любу ізотермічну поверхню твердого тіла (нерухомого газу чи рідини) в напрямку другої ізотермічної поверхні, повинно бути прямо пропорціональне часу, площі ізотермічної поверхні, різниці температур і обернено пропорційним відстані між цими ізотермічними поверхнями. У математичній формі це можна записати так:

(1.2)

де Q_? – вектор кількості теплоти, що проходить крізь тіло, Дж; λ – теплопровідність, Вт/(м·К); F – площа (рис.1.1), перпендикулярна до нормалі ізотермічної поверхні м². (Знак “–” вводиться в формулу тому, що вектор кількості теплоти у відповідності з другим законом термодинаміки повинен бути спрямованим в бік зменшення температури).

Формула (1.2), не дивлячись на те, що вона є узагальненням гіпотези Біо, відома зараз як закон Фур’є.

Величина

(1.3)

де Q = dQ_τ/d_τ – вектор теплового потоку, Дж/с; називається в теорії теплообміну інтенсивністю теплового потоку, Вт/м².

З рис.1.1 видно, що похідна температури по напрямку ℓ зв’язана з градієнтом температури очевидним співвідношенням

(1.4)

де cos(n,?) – косинус кута між нормаллю до ізотермічної поверхні п і напрямком ℓ.

Необхідно зауважити, що похідна температури по напрямку ℓ визначається через похідні температури за декартовими координатами формулою:

(1.5)

де cos(х,ℓ), cos(у,ℓ) і cos(z,ℓ) – косинуси кутів між напрямком ℓ і координатними осями х, у і z.

З урахуванням (1.4) закон Фур’є (1.2) можна записати в такому вигляді:

(1.6)

де ds = dF cos(n,ℓ) – елементарна площадка, перпендикулярна до напрямку ℓ.

1.2. Теплопровідність речовин

Теплопровідність λ у формулі (1.2) з математичної точки зору являє собою коефіцієнт пропорціональності, чия роль криється в рівнянні розмірності лівої і правої частин закону Фур’є і вимірюється в Вт/(м·К).

З фізичної точки зору теплопровідність – теплофізична характеристика речовини. Для різних речовин при однакових градієнтах температури, поверхнях F і часі ? кількість теплоти, яка проходить через тіло, визначається тільки коефіцієнтом ?. Чим більша теплопровідність, тим більшою буде властивість речовини проводити теплоту, і навпаки. Кажучи іншими словами, теплопровідність представляє собою теплофізичний параметр, який визначає спосібність тіл проводити теплоту.

Для одного і того ж матеріалу теплопровідність змінюється в досить широких межах, при цьому характер зміни визначається багатьма факторами: температурою, кількістю домішок, наявністю вологи, тиском та ін. Зазвичай, залежність λ від перерахованих факторів не підлягає строгому аналітичному опису, виходячи з цього основним джерелом отримання достовірних значень теплопровідності залишається експеримент.

1.3. Диференціальне рівняння теплопровідності

Диференціальним рівнянням теплопровідності називається виражений в математичній формі перший закон термодинаміки для тіл, процес взаємодії яких з навколишнім середовищем відбувається без здійснення зовнішньої роботи.

Для складання диференціального рівняння теплопровідності розглянемо нерівномірно нагріте тіло, наведене на рис.1.2. Вважаємо, що поверхня цього тіла S, а об’єм V.

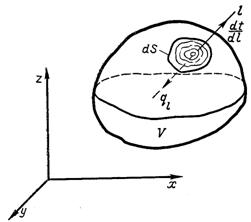
Рис.1.2. До виводу диференціального рівняння теплопровідності

Якщо температура тіла внаслідок певних причин зміниться і стане відмінною від температури навкілля, між тілом і середовищем починається процес теплообміну. Перший закон термодинаміки для цього випадку запишеться в такому вигляді:

Q_ст + Q_V = ΔU + W, (1.7)

де Q_ст – кількість теплоти, отримане (чи віддане) тілом через поверхню; Q_V – кількість теплоти, яка виділяється (чи поглинається) в тілі за рахунок дії внутрішніх джерел (чи стоків) теплоти; ?U – зміна внутрішньої енергії; W – робота, виконана тілом в навколишньому середовищі, чи навпаки. У відповідності з прийнятим визначенням механічна робота дорівнює нулю W=0.

Кількість теплоти Q_ст можна вирахувати за формулою:

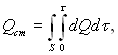(1.8)

а Q_V визначається за співвідношенням:

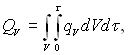(1.9)

де q_V – питома потужність внутрішніх джерел (стоків) теплоти, Вт/м³.

Зміна внутрішньої енергії тіла

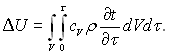(1.10)

З урахуванням рівнянь (1.8), (1.9) і (1.10) залежність (1.7) набуває вигляду

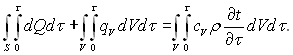(1.11)

Перший член лівої частини (1.11) у відповідності з формулами (1.5) і (1.6) можна представити в розгорнутому вигляді:

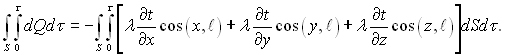(1.12)

Застосувавши до (1.12) перетворення Остроградського, отримаємо:

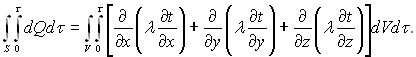(1.13)

Далі підставляємо (1.13) в (1.11), отримаємо:

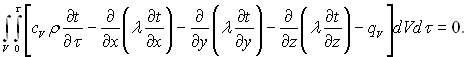(1.14)

Якщо всі члени рівняння (1.14) – безперервні функції координат і часу, то інтеграл дорівнює нулю при рівності нулю підінтегрального виразу. У цьому разі

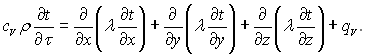(1.15)

Диференціальне рівняння (1.15) називається диференціальним рівнянням Фур’є-Кірхгофа, яке виявляє зв’язок між часовою і просторовою зміною температури у довільній точці тіла. При усталеній теплопровідності рівняння (1.15) спрощується:

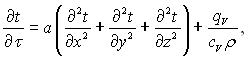(1.16)

де a = λ/(c_V?) – ізохорна температуропровідність, м²/с.

Ізохорна температуропровідність, яка входить в (1.16) є теплофізичним параметром. Вона характеризує спроможність речовини вирівнювати температуру. Це значить, що тіла, які мають велику температуропровідність, нагріваються (охолоджуються) скоріше в порівнянні з тілами, що мають меншу температуропровідність.

Рівняння (1.16) є лінійне диференціальне рівняння в частинних похідних другого порядку параболічного типу. Для анізотропних тіл, у яких теплопровідність залежить від напрямку, рівняння Фур’є-Кірхгофа набуває наступного вигляду:

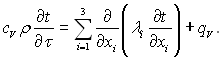(1.17)

Якщо величини ? і c_V в анізотропному тілі не залежать від температури, то рівняння (1.17) після перетворення, приймаючи що можна привести до вигляду (1.16).

Рис.1.3.Циліндричні (а) і сферичні (б) координати

Диференціальне рівняння теплопровідності (1.15) має вид: в циліндричній системі координат (рис.1.3, а)

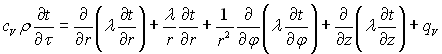(1.18)

і при ? = const

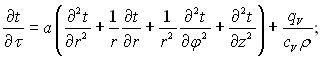(1.19)

у сферичній системі координат (рис.1.3, б)

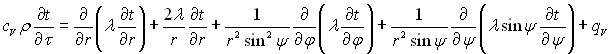(1.20)

і при ? = const

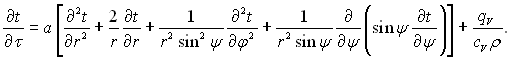(1.21)

1.4. Умови однозначності

Отримане диференціальне рівняння (1.15) описує множину явищ теплопровідності. Щоб із безмежної кількості цих явищ виділити одне і дати його повний математичний опис, до диференціального рівняння теплопровідності необхідно добавити умови однозначності, які містять у собі геометричні, фізичні, часові і граничні умови.

Геометричні умови визначають форму і розміри тіла, в якому відбувається досліджуваний процес.

Фізичні умови задаються теплофізичними параметрами тіла λ, c_V і розподілом внутрішніх джерел теплоти.

Часові (початкові) умови містять розподіл температури в тілі в початковий момент часу.

Граничні умови визначають особливості проходження процесу на поверхні тіла. Граничні умови можуть задаватися декількома способами.

Граничні умови І роду. У цьому випадку задається розподіл температури на поверхні тіла для кожного моменту часу:

t_ст = f(х_ст, у_ст, z_ст, τ), (1.22)

де t_ст – температура поверхні тіла; х_ст, у_ст, z_ст – координати поверхні тіла.

В окремих випадках, коли температура на поверхні тіла не змінюється в часі t_ст = f(х_ст, у_ст, z_ст), і якщо вона постійна на поверхні, то t_ст = const.

Граничні умови ІІ роду. У цьому випадку задається величина теплового потоку для кожної точки поверхні тіла в довільний момент часу, цебто

q_ст = f(х_ст, у_ст, z_ст, τ). (1.23)

В окремих випадках, наприклад при нагріванні металевих виробів у високотемпературних печах q_ст = const.

Граничні умови ІІІ роду. У цьому випадку задаються температури середовища t_о і умови теплообміну цього середовища з поверхнею тіла.

Процеси теплообміну між середовищем і тілом є винятково складними і залежать від багатьох факторів. Докладніше вони розглянуті у другій часині книги. Для опису інтенсивності теплообміну між поверхнею тіла і середовищем використовується гіпотеза Ньютона-Ріхмана, згідно з якою

q_ст = α(t_ст – t_о), (1.24)

де α – коефіцієнт пропорціональності, названий коефіцієнтом тепловіддачі, Вт/(м²·К).

Як видно із формули (1.24), коефіцієнт тепловіддачі чисельно рівний кількості теплоти, яка віддається (чи сприймається) одиницею поверхні тіла в одиницю часу при різниці температур між поверхнею тіла і навколишнім середовищем, рівною 1 град.

З урахуванням (1.24) і (1.3) гранична умова ІІІ роду записується так:

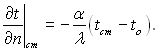(1.25)

У разі, коли коефіцієнт тепловіддачі має великі значення (наприклад, під час кипіння рідини на поверхні тіла), граничні умови ІІІ роду переходять в граничні умови І роду, тому що у цьому випадку температура поверхні тіла стає практично рівною температурі рідини.

Граничні умови ІV роду формуються на основі рівності теплових потоків, які проходять крізь прилеглі одна до іншої поверхні тіл, тоді

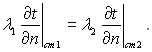(1.26)

При досконалому тепловому контакті обидва тіла на поверхні дотику мають однакову температуру, це значить, що ізотерми безперервно переходять з одного тіла до іншого, при цьому градієнти температур у цих точках задовольняють умову (1.26)

Диференціальне рівняння (1.15) разом з умовами однозначності дають повне математичне формулювання конкретної задачі теплопровідності. Розв’язок цієї задачі може виконуватися аналітичним, чисельним чи дослідним методами. В останньому випадку використовуються методи подібності і аналогій.