




Розділ 2. СТАЦІОНАРНА ТЕПЛОПРОВІДНІСТЬ
2.1. Загальне диференціальне рівняння одномірного температурного поля для необмеженої плоскої стінки, необмеженого циліндра і кулі
При стаціонарному режимі температурне поле не залежить від часу дt/дτ=0 і диференціальне рівняння теплопровідності (1.15) набуває вигляду
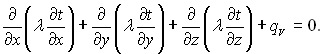 (2.1)
(2.1)
Розглянемо декілька випадків коли температура тільки від одної координати.
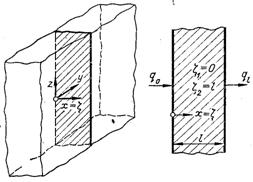
Рис.2.1. Необмежена плоска стінка
Необмежена плоска стінка (рис.2.1) являє собою тіло, обмежене з двох сторін паралельними поверхнями, протяжність яких у напрямку у і z велика. Якщо бокові стінки необмеженої плоскої стінки ізотермічні, то зміною температури в ній по осям у і z можна знехтувати (дt/ду = дt/дz = 0) і диференціальне рівняння теплопровідності (2.1) приймає вигляд
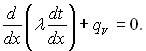 (2.2)
(2.2)
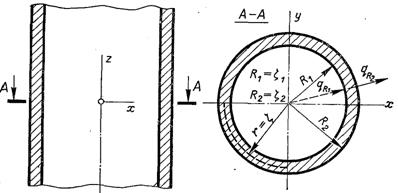
Рис.2.2.Необмежений порожнистий циліндр
Тіло циліндричної форми (рис.2.2) протяжність якого по осі z велика, називається необмеженим циліндром, який може бути суцільним (R1 = 0) і порожнистим (R1 ≠ 0). Як для суцільного, так і для порожнистого необмежених циліндрів у тому випадку, коли внутрішні і зовнішні поверхні є ізотермічними, маємо дt/дz = дt/дφ = 0, (r2 = x2 + y2) і диференціальне рівняння теплопровідності набуває вигляду:
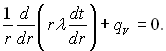 (2.3)
(2.3)
У випадку ізотермічної внутрішньої і зовнішньої поверхонь для порожнистої кулі (рис.2.3) маємо дt/дφ = дt/дψ = 0, (r2 = x2 + y2 + z2). Отже, диференціальне рівняння теплопровідності в цьому випадку записується наступним чином:
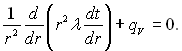 (2.4)
(2.4)
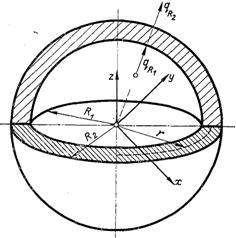
Рис.2.3. Порожниста куля
Не важко замітити, що диференціальні рівняння теплопровідності (2.2), (2.3) і (2.4) можна об’єднати в одне:
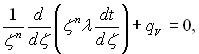 (2.5)
(2.5)
де ζ – узагальнююча координата.
При ζ = х (п = 0) диференціальне рівняння теплопровідності (2.5) переходить в диференціальне рівняння теплопровідності (2.2), при ζ = r (п = 1) – в (2.3) і при ζ = r (п = 2) – в (2.4).
2.2. Температурне поле в тілі з постійно діючим внутрішнім джерелом теплоти, питома потужність якого – довільна функція температури
Загальний розв’язок одномірного диференціального рівняння теплопровідності (2.5) у випадку, коли внутрішні джерела теплоти залежать від координати, має вигляд:
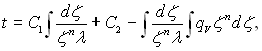
а при
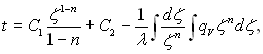 (2.6)
(2.6)
де С1 і С2 – сталі інтегрування.
Нехай на поверхні тіла тепловіддача визначається граничними умовами ІІІ роду. Тоді для знаходження сталих інтегрування в (2.6) можна скласти систему:
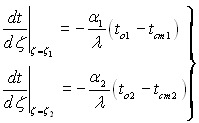 , (2.7)
, (2.7)
де α1, to1, α2, to2 – коефіцієнти тепловіддачі і температури середовищ, які обмивають поверхню тіла; ζ1, ζ2 – узагальнені координати поверхонь тіла; tст1, tст2 – невідомі температури поверхонь.
Якщо підставити в систему (2.7) загального розв’язку з рівняння (2.6), то система набуде такого вигляду:
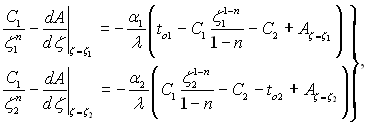 (2.8)
(2.8)
де 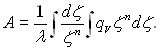 (2.9)
(2.9)
Із розв’язку системи (2.8) виходить, що
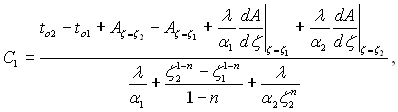 (2.10)
(2.10)
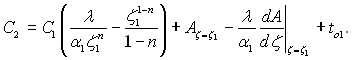 (2.11)
(2.11)
Підставляючи (2.10) і (2.11) в загальний розв’язок (2.6), отримаємо формулу температурного поля в тілі:
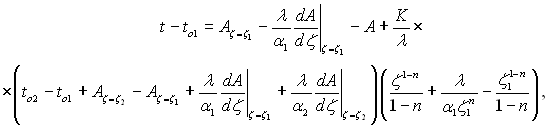 (2.12)
(2.12)
де 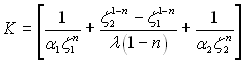 – коефіцієнт теплопередачі.
– коефіцієнт теплопередачі.
Якщо диференціювати (2.12) по координаті ζ і підставити отриману при цьому похідну в закон Фур’є (1.3), отримаємо формулу для густини теплового потоку:
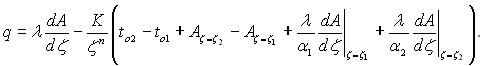 (2.13)
(2.13)
Як зауважувалося раніше, граничні умови ІІІ роду переходять в граничні умови І роду при α→∞. Приймаючи у формулах (2.12) і (2.13) α1→∞ і α2→∞, отримаємо розрахункові формули узагальненого одномірного температурного поля для граничних умов І роду:
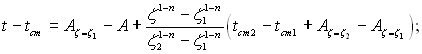 (2.14)
(2.14)
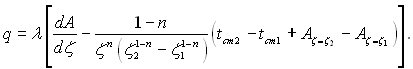 (2.15)
(2.15)
2.3. Температурне поле в тілі з теплопровідністю, яка залежить від температури, і з постійно діючим внутрішнім джерелом теплоти, питома потужність якого – довільна функція координати
У цьому випадку загальний розв’язок диференціального рівняння теплопровідності (2.5) записується в наступному вигляді:
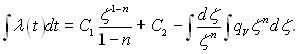 (2.16)
(2.16)
Якщо теплопровідність – функція температури виду
![]() (2.17)
(2.17)
де λ0 – теплопровідність при t = 0 °С; а, b, c – дослідні сталі, а тепловіддача на поверхні визначається граничними умовами І роду. Тоді загальний розв’язок (2.16) можна записати так:
![]() (2.18)
(2.18)
де 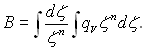
Сталі інтегрування в (2.18) визначаються з граничних умов
ζ = ζ1 і t = tcт1; ζ = ζ2 і і t = tcт2. (2.20)
Пропускаючи нескладні проміжні викладки, отримаємо в підсумку
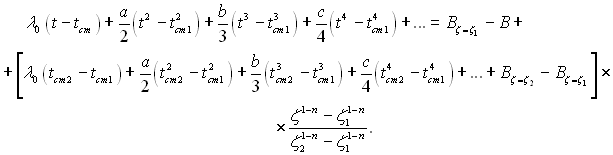 (2.21)
(2.21)
Після диференціювання по ζ формули (2.21) і підставляючи далі похідну в узагальнюючий закон Фур’є:
![]() (2.22)
(2.22)
отримаємо
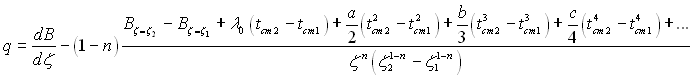 (2.23)
(2.23)
Для більш складних граничних умов роздільне визначення сталих інтегрування С1 і С2 в загальному розв’язку (2.16) дуже ємне і з цієї причини отримати в явному вигляді формули типу (2.21) і (2.23) не удається. Введемо до розгляду перетворення Кірхгофа, яке визначається формулою
![]() (2.24)
(2.24)
де λсер – середнє значення теплопровідності; и – змінна, яка залежить від температури.
Для граничних умовах І роду можна (2.24) інтегрувати, внаслідок чого отримаємо:
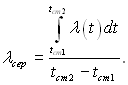 (2.25)
(2.25)
Далі, з урахуванням (2.24) початкову функцію (2.16) можна записати так:
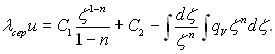 (2.26)
(2.26)
Розв’язок (2.26) при граничних умовах І роду визначається формулою (2.12) при α1→ ∞ α2→ ∞ і з заміною в ній λ на λсер, тобто
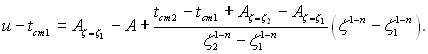 (2.27)
(2.27)
Після диференціювання (2.27) по ζ і приймаючи до уваги, що перетворення Кірхгофа (2.24) тотожне густині теплового потоку, взятого зі зворотним знаком, отримаємо
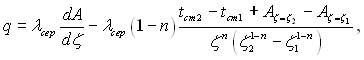 (2.28)
(2.28)
де А визначається згідно (2.9) з заміною λ на λсер.
Формула (2.28) дозволяє розраховувати густину теплового потоку практично при любій заданій залежності коефіцієнта теплопровідності від температури, тому що величина середньої теплопровідності λсер, яка входить до неї визначається формулою (2.25).
Наприклад, формули (2.21) і (2.23) для необмеженого порожнистого циліндра з внутрішнім R1 і зовнішнім R2 радіусами, якщо питома потужність постійно діючого внутрішнього джерела теплоти в ньому постійна і рівна qV, а коефіцієнт теплопровідності – лінійна функція температури
λ = λо(1+аt), (2.29)
будуть мати вигляд
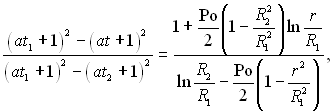 (2.30)
(2.30)
а для лінійного теплового потоку
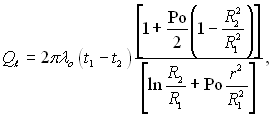 (2.31)
(2.31)
де 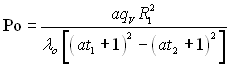 – число подібності Померанцева.
– число подібності Померанцева.
2.4. Температурне поле в тілі з постійно діючим внутрішнім джерелом теплоти, питома потужність якого – функція температури виду qV = w0(1 + bt)
У цьому випадку диференціальне рівняння теплопровідності (2.5) запишеться так:
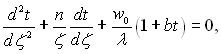 (2.32)
(2.32)
де w0 – питома потужність постійно діючого внутрішнього джерела теплоти при t = 0 °С; b – дослідна стала величина. При
![]() (2.33)
(2.33)
де ![]() (2.32) перетворюється до виразу
(2.32) перетворюється до виразу
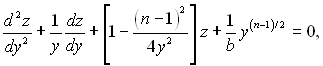 (2.34)
(2.34)
який представляє собою неоднорідне рівняння Бесселя. Його загальний розв’язок можна виразити початковою функцією виду
![]() (2.35)
(2.35)
чи з урахуванням підстановки (2.33) – функцією
![]() (2.36)
(2.36)
де ![]() – функції Бесселя І і ІІ роду, порядку (п –1)/2, аргументу
– функції Бесселя І і ІІ роду, порядку (п –1)/2, аргументу ![]()
Наприклад, для кулі (п = 2 і ζ = r) формула (2.36) приймає вигляд
![]() (2.37)
(2.37)
За допомогою співвідношень
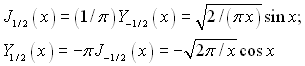 (2.38)
(2.38)
(2.37) перетворюється далі до наступного вигляду:
![]() (2.39)
(2.39)
де А і В – сталі інтегрування.
Припустимо, що на поверхні порожнистої кулі тепловіддача характеризується граничними умовами І роду: рівняння (2.20) при ζ1 = R1 і ζ2 = R2. У цьому випадку сталі інтегрування А і В можна визначити з системи
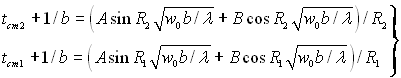 (2.40)
(2.40)
Розв’язуємо систему (2.40) відносно А і В і підставимо знайдені вирази в (2.39) і отримаємо формулу температурного поля в порожнистій кулі
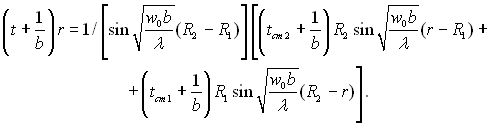 (2.41)
(2.41)
Розподіл температур, який розраховується за (2.41), має одну особливість, а саме: температура може обертатися тут в нескінченність при
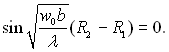 (2.42)
(2.42)
Із (2.42) виходить, що
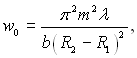 (2.43)
(2.43)
де т =0, 1, 2, 3,...
При т = 0 (w0 = 0) отримаємо у формулі температурного поля (2.41) невизначеність типу нуль на нуль. Цей випадок повинен відповідати розподілу температури в порожнистій кулі без внутрішнього джерела теплоти. При т = 1 отримаємо
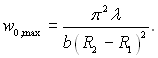 (2.44)
(2.44)
Якщо питома потужність постійно діючого внутрішнього джерела теплоти перевищить w0,max, тепловий потік з поверхні кулі при заданих tст1 і tст2 не можна буде відвести і відбудеться руйнування матеріалу. На цей момент необхідно звертати увагу і при аналізі температурного поля необмеженої плоскої стінки і необмеженого циліндра.
2.5. Температурне поле в складовій системі з постійними внутрішніми джерелами теплоти
Під складовою системою розуміємо тіло, яке складається із щільно приєднаних між собою чи необмежених плоских стінок, чи необмежених плоских циліндрів, чи порожнистих кульових поверхонь. У загальному випадку товщини і коефіцієнти теплопровідності тіл, з яких складається система, можуть відрізнятися один від іншого.
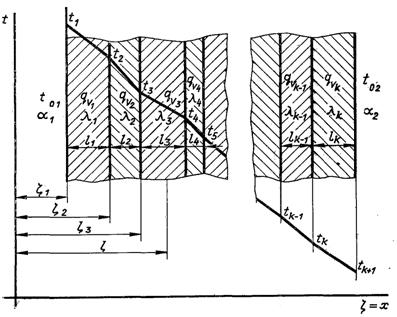
Рис.2.4. Складова плоска стінка
На рис.2.4 наведена складова (багатошарова) плоска система, яка складається із k необмежених плоских стінок з різною товщиною і різними коефіцієнтами теплопровідності: у кожній пластині постійно діє внутрішнє джерело теплоти з постійною питомою потужністю.
Температурне поле в складовій системі повинно характеризуватися системою початкових функцій виду
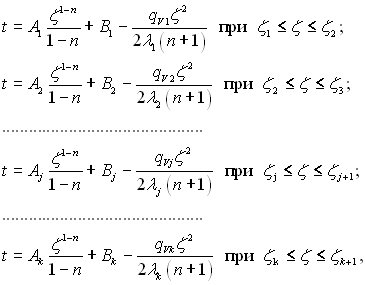 (2.45)
(2.45)
де А1, В1, А2, В2, ... , Аk, Вk – сталі інтегрування; qV1, qV2, qV3, …, qVk – усталені питомі потужності внутрішніх джерел теплоти.
Якщо на поверхні складової системи тепловіддача визначається граничними умовами ІІІ роду, систему рівнянь для знаходження 2k сталих інтегрування в (2.45) можна скласти наступним чином.
Два рівняння отримуються з умови теплообміну на зовнішніх поверхнях складової системи і мають вигляд:
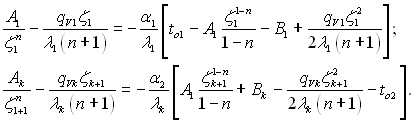 (2.46)
(2.46)
Для k – 1 рівнянь визначаються з умови стиковки за температурою в площині контакту. Вигляд цих рівнянь наступний:
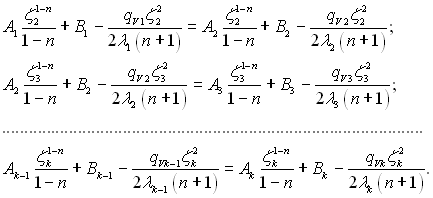 (2.47)
(2.47)
Інші k – 1 рівнянь складаються з умови стиковки по густині теплового потоку. Вони записуються так:
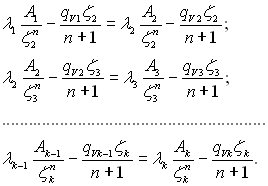 (2.48)
(2.48)
Умови (2.47) і (2.48) виконуються при ідеальному тепловому контакті поверхонь. У реальних умовах можуть виникати додаткові контактні термічні опори, величини яких залежать від технологічних і конструкторських факторів.
Розв’язок системи рівнянь (2.46)...(2.48) відносно сталих інтегрування дуже громіздке і нами не розглядається. Кінцевий результат для температури в j-му тілі складової системи такий:
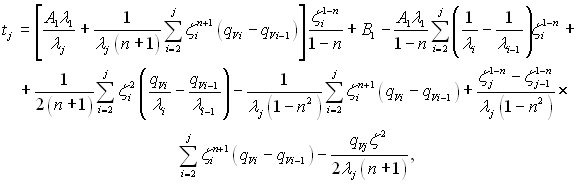 (2.49)
(2.49)
де
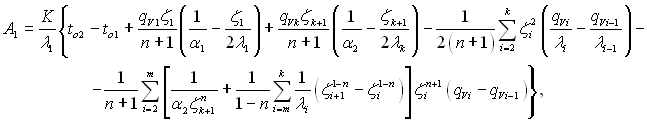
(2.50)
де К – коефіцієнт теплопередачі системи; т = 2, 3, 4, ... , k;
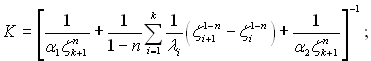 (2.51)
(2.51)
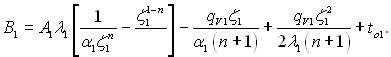 (2.52)
(2.52)
При qV1 = qV2 = qV3 = … = 0 формула (2.49) суттєво спрощується:
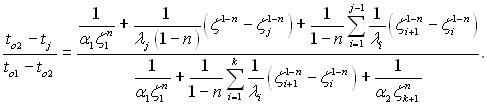 (2.53)
(2.53)
Як видно, формула (2.53) представляє собою рівняння прямої лінії у відрізках. Через це поточну температуру в складовій системі без внутрішніх джерел теплоти можна визначати графічним шляхом (рис.2.5)
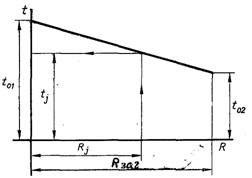
Рис.2.5. Графічне визначення температури у складовій стінці
Для цього по горизонтальній осі в довільному масштабі відкладаємо відрізок
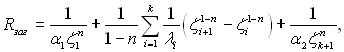
який в теорії теплообміну називається термічним опором. З кінців цього відрізку ставимо перпендикуляри, на яких в масштабі Rзаг, наносяться температури to1 і to2. Пряма, яка з’єднує кінці відрізків температур to1 і to2, представляє собою температурне поле в складовій системі.
Температура в довільній точці внутрішньої площини j-го тіла визначається так. Із початку відрізка Rзаг відкладається відрізок
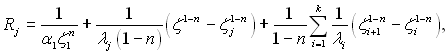
який, за своєю суттю є термічним опором складової системи до перерізу, що визначається поточною координатою ζ. З кінця відрізку Rj ставимо перпендикуляр до перетину з прямою температури. Величина цього перпендикуляра в масштабі вертикальної осі є шуканою температурою.
Диференціювання по ζ (2.53) і підстановка похідної в узагальнюючий закон Фур’є (2.22), дозволяє отримати формулу для густини теплового потоку, який проходить крізь складову систему, внутрішні джерела теплоти в якій відсутні:
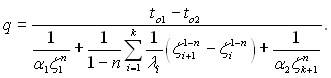 (2.54)
(2.54)
Як окремий випадок, із (2.54) отримуємо наступні формули:
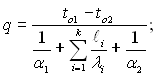 (2.55)
(2.55)
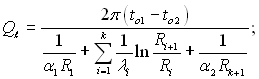 (2.56)
(2.56)
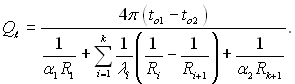 (2.57)
(2.57)