2.6. Ребристі поверхні

Із закону Фур’є (1.2) виходить, що чим більша поверхня F знімання теплоти, тим більша кількість теплоти пройде через неї і розвіється в навколишньому середовищі. Цей факт часто використовується при вирішені питань охолодження електронних приладів, в холодильних установках та ін.

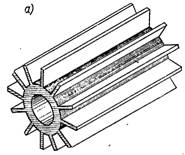
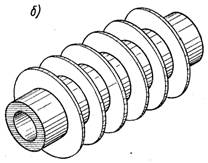
Рис.2.6. Конструкції ребер

Поверхня тіла збільшується за допомогою ребер, наприклад прямих (рис.2.6, а) чи кільцевих (рис.2.6, б) довільної конфігурації. Зазвичай, найбільш ефективне оребреня визначається формою, розмірами, вартістю та ін. кожної конкретної установки і вибираються індивідуально.

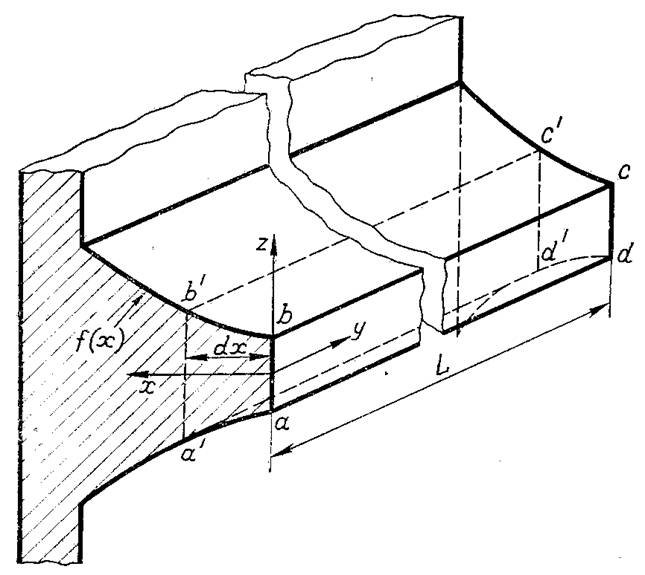
Рис.2.7. Пряме ребро довільного профілю

Розглянемо пряме ребро довільного профілю (рис.2.7). Вважаємо, що розподіл температури за товщиною ребра рівномірний (температура змінюється тільки за координатою х). У цьому випадку кількість теплоти, яка проходить через переріз ребра розраховується за законом Фур’є. Для розгляду умов

(2.58)

вважаємо, що f(x) становить половину товщини ребра в перерізі a'b'c'd'.

При стаціонарному режимі така ж кількість теплоти буде віддаватися в навколишнє середовище конвекцією. Якщо вважати, що елементарна поверхня становить 2Ldx, теплові втрати конвекцією можуть визначатися за законом Ньютона-Ріхмана:

(2.59)

Додаючи (2.58) і (2.59), отримаємо диференціальне рівняння, яке характеризує теплообмін в прямому ребрі довільного профілю,

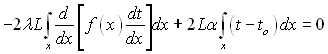
звідки

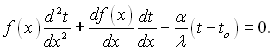(2.60)

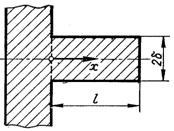
Рис.2.8. Пряме ребро прямокутного профілю

Пряме ребро прямокутного профілю (рис.2.8). У цьому випадку f(x) = δ і, як наслідок, (2.60) спрощується:

  (2.61)

де – комплекс.

Загальний розв’язок (2.61) виражається початковою функцією типу

(2.62)

Якщо знехтувати тепловіддачею з поверхні вершини ребра (х = δ) и вважати температуру основи ребра (х = 0) рівною t_осн, отримаємо, пропустивши проміжні викладки,

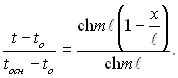(2.63)

Формула (2.63) характеризує температурне поле в ребрі прямокутного профілю при розглянутих граничних умовах.

Показником робочої характеристики ребра є його ефективність. Під цим поняттям слід розуміти відношення повного теплового потоку, який передається через ребро, до того теплового потоку, який передавався б через ребро у випадку, коли б вся поверхня ребра знаходилась би при температурі t_осн.

Повний тепловий потік, який проходить крізь ребро і той, що розвіюється з його поверхні, визначається з урахуванням (2.63) за формулою

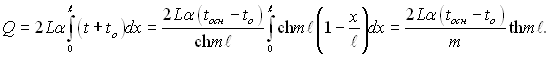 (2.64)

Тепловий потік, який розвіювався б з поверхні ребра, якби воно знаходилось при постійній температурі t_осн, визначається виразом

(2.65)

Розділивши (2.64) на (2.65), отримаємо формулу для ефективності ребра прямокутного профілю

(2.66)

де ξ – коефіцієнт ефективності ребра прямокутної форми.

Ефективність ребра, як це слідує з (2.66), змінюється від 0 до 1; значення ξ  = 1 відповідає ідеальному випадку, коли температура всієї поверхні ребра дорівнює температурі його основи. Це свідчить про максимальне теплове знімання з поверхні ребра.

За величиною ефективності ребра зручно судити про вплив довжини ребра, теплопровідності, коефіцієнта тепловіддачі та ін. на інтенсивність використання тепла. Так, наприклад, при тℓ = 1 ефективність ребра становить ξ  = 0,716, а при значенні тℓ = 0,5 становитиме вже 0,924. Зменшити параметр тℓ , а значить, і підвищити ефективність ребра можна, наприклад, за рахунок збільшення теплопровідності, зменшення коефіцієнта тепловіддачі, зменшення довжини ребра і збільшення його товщини.

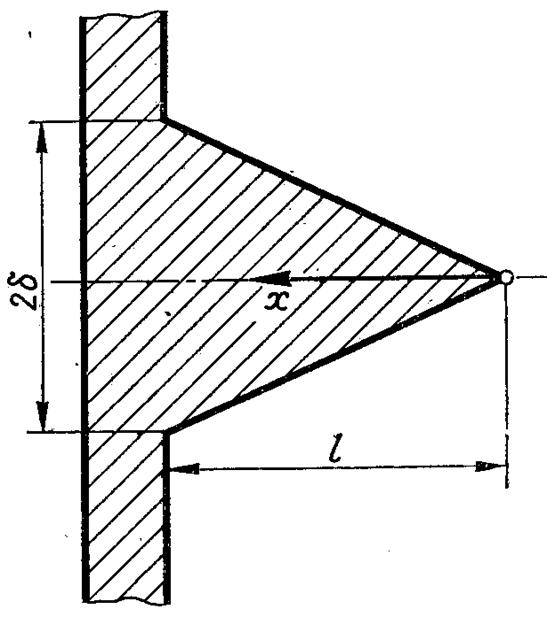
Рис.2.9. Пряме ребро трикутного профілю

Пряме ребро трикутного профілю (рис.2.9). Для ребра цієї форми f(x) = (x/ℓ)δ  тоді (2.60) набуває вигляду

(2.67)

Диференціальне рівняння (2.67) представляє собою одну із форм модифікованого рівняння Бесселя. Його загальним розв’язком може служити початкова функція виду

(2.68)

де – модифіковані функції Бесселя нульового порядку, І і ІІ роду, аргументу 

Вважаючи, як і для прямого ребра прямокутного профілю, температуру в основі (х = ℓ) рівною t_осн і нехтуючи тепловіддачею з торця (х = 0), можна (2.68) привести до кінцевого вигляду

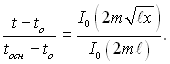(2.69)

Повний тепловий потік, який проходить крізь ребро трикутного профілю, розраховується по формулі

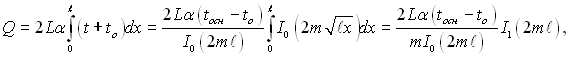(2.70)

де І₀(2тℓ) – модифікована функція І роду 1-го порядку аргументу 2тℓ [під час розрахунку інтеграла використовують рекурентну формулу .

Знаючи (2.70) можна вирахувати ефективність ребра трикутного профілю:

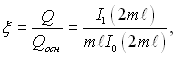(2.71)

де Q_осн визначається за (2.65).

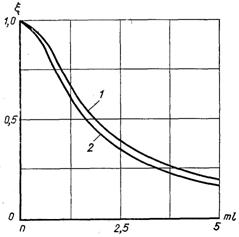
Рис.2.10. Порівняння ефективності прямих ребер:1 – прямокутний і 2 – трикутний профілі

При однакових коефіцієнтах тепловіддачі, теплопровідності, товщині і висоті прямокутне ребро ефективніше ребра трикутного профілю (рис.2.10). Але варто мати на увазі, що трикутне ребро при однаковій с прямокутним ребром висотою і товщині основи менш метало ємне, а значить дешевше. При визначенні ефективності ребра з цієї точки зору трикутному ребру необхідно віддати переваги.

Рис.2.11. Кругле ребро прямокутного профілю

Кругле ребро прямокутного профілю (рис.2.11).

Аналіз виконуємо так само, як і для прямого ребра. Рівняння (2.58) для цього випадку буде

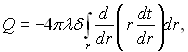(2.72)

а (2.59) можна записати так:

(2.73)

Додаючи (2.72) і (2.73), отримаємо диференціальне рівняння теплопровідності для круглого ребра прямокутного перерізу у наступній формі:

(2.74)

Рівняння (2.74) є модифіковане рівняння Бесселя тому

 (2.75)

Сталі інтегрування С₁ і С₂ визначаємо, виходячи з тих самих граничних умов, які використовувалися під час аналізу прямих ребер. Це приводить у кінцевому підсумку до залежності:

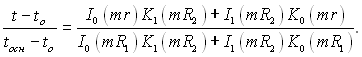 (2.76)

Дисипований (розсіяний) з поверхні кільцевого ребра тепловий потік визначається, як і вище, за законом Ньютона-Ріхмана, який в даному випадку має вигляд:

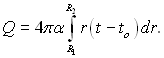 (2.77)

Щоб взяти інтеграл в (2.77), необхідно використати рекурентну формулу [див. пояснення до (2.70)]. При цьому в підсумку отримаємо:

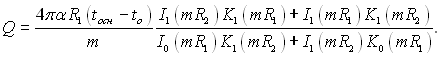(2.78)

Тепловий потік, дисипований з поверхні кільцевого ребра, коли температура його скрізь дорівнює t_осн, розраховується за формулою (2.77) з заміною t на t_осн:

(2.79)

Таким чином, ефективність кільцевого ребра прямокутного профілю

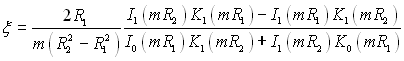. (2.80)

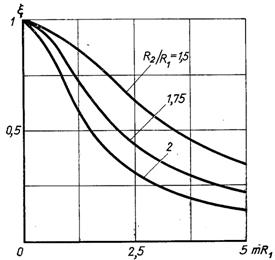
Рис.2.12. Вплив параметра тR₁ на ефективність кругового ребра прямокутного профілю

Формула (2.80) представлена на рис.2.12. Як видно, зменшення параметра тR₁ (що рівносильне збільшенню теплопровідності, товщині ребра, зменшенню радіуса труби і коефіцієнта тепловіддачі) тягне за собою збільшення ефективності.

2.7. Двомірне температурне поле

Двомірне температурне поле може виникати у тілах обмежених чи плоскими, чи сумісно циліндричними і плоскими поверхнями, іншими словами в плоских напівобмежених стінках, пластинах, напівобмежених і обмежених суцільних і порожнистих циліндрах.

Диференціальне рівняння, яке відповідає цьому випадку, можна отримати з (1.16) з урахуванням (2.5)

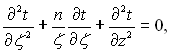  (2.81)

де п = 0 для напівобмежених плоских тіл і пластин, п = 1 для напівобмежених і обмежених суцільних і порожнистих циліндрів.

Шукаємо загальне рішення (2.81) у наступній формі (метод розділу змінних – метод Фур’є)

t =EZ, (2.82)

де Е – функція, яка залежить тільки від ζ; Z – функція, яка залежить тільки від z.

Підстановка (2.82) в (2.81) дає

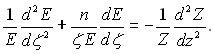(2.83)

У лівій і правій частинах (2.83) знаходяться функції, які залежать від незалежних між собою змінних. На цій підставі рівність в (2.83) може бути льки у тому випадку, якщо ліва і права частини цього співвідношення дорівнюють якій-небудь одній і тій же сталій. Позначимо її через р². Тоді замість (2.83)отримаємо два диференціальних рівняння:

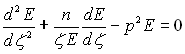(2.84)

і

(2.85)

Диференціальне рівняння (2.84) представляє собою одну із форм модифікованого рівняння Бесселя. Його загальне рішення можна виразити функцією

(2.86)

Загальний розв’язок диференціального рівняння (2.85) – початкова функція виду

 (2.87)

Таким чином, загальний розв’язок диференціального рівняння теплопровідності (2.81) такий:

(2.88)

Нехай температура на боковій поверхні обмеженого суцільного циліндра з радіусом R і довжиною ℓ постійна і рівна t_п, а на торцевих поверхнях (z=0 і z=ℓ) дорівнює нулю. З умови рівності нулю температури на торцях циліндра отримаємо С₄=0 і

р = πт/ℓ, (2.89)

де т = 0, 1, 2, 3,... .

Крім цього, С₂ = 0, тому що температура на осі циліндра кінцева величина, а модифікована функція Бесселя K₀(pr) прямує до нескінченності при r→0 (для циліндра при п = 1 ζ = r).

Рівняння (2.89) має множину корнів. Отже, розв’язок диференціального рівняння теплопровідності (2.81) для циліндра буде функцією виду

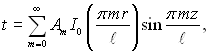 (2.90)

де А_т – стала величина.

Якщо перепишемо R = r ряд (2.90) в розгорнутій формі, далі помножимо праву і ліву частини отриманого при цьому виразу на sin (πmz/ℓ) і проінтегруємо його від 0 до ℓ, отримаємо:

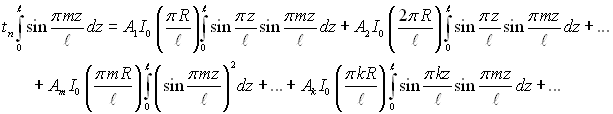(2.91)

В теорії рядів Фур’є показано, що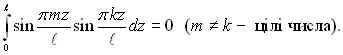

Отже, ряд (2.91) спрощується до

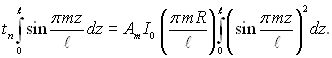(2.92)

Із (2.92) знаходимо А_т:

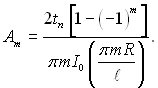(2.93)

Підставляючи (2.93) в (2.90), отримаємо

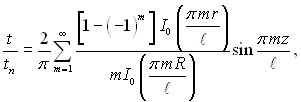(2.94)

чи у кінцевому вигляді

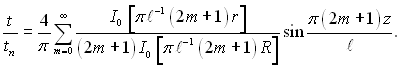(2.95)

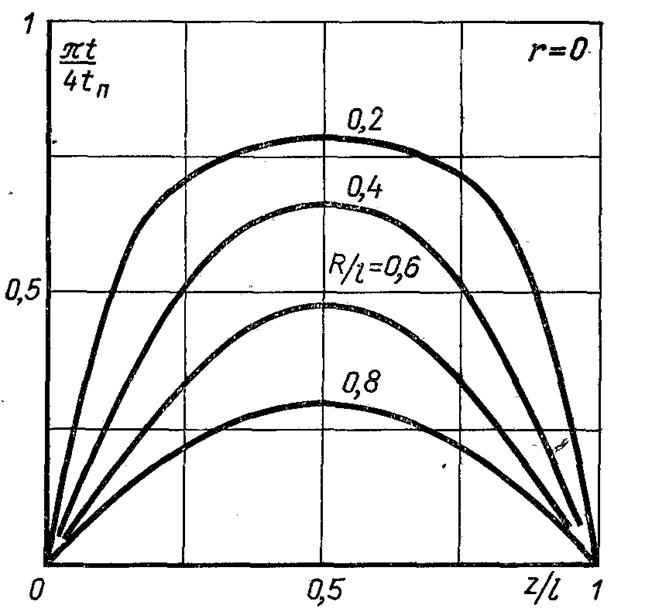
Рис.2.13.Розподіл температури в суцільному обмеженому циліндрі за нульової температури торців

На рис.2.13 представлене поле температур на осі обмеженого суцільного циліндра, побудоване по (2.94).

Розглянемо випадок коли на торці (z = 0) обмеженого суцільного циліндра температура рівна t_m1, а на іншому торці (z = ℓ) і поверхні (r=R) – нулю. У цьому разі при поділі виразу (2.83) на два диференціальних рівняння сталу зручно позначати через р². Тоді розв’язок (2.81) для циліндра записується так:

(2.95)

З умови обмеження температури при r=0  отримуємо С₂=0, а з умови рівності нулю температури на торці (z = ℓ) С₃ = –С₄е^–2рℓ. Таким чином, (2.95) спрощується до

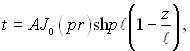(2.96)

де А – стала інтегрування.

Рівності нулю температури на боковій поверхні (2.96) можна задовольнити, якщо параметр р визначати з рівняння (табл.2.1 при →∞) J₀(pR)= 0.

Таблиця 2.1. Корні характеристичного рівняння pRJ₁(pR) – BiJ₀(pR) = 0

Продовження таблиці 2.1

Тому що J₀(pR) = 0 має множину корнів, то

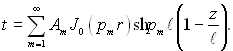(2.97)

Розгорнемо ряд (2.97) при z = 0, далі помножимо ліву і праву частину його на rJ₀(p_mr) і проінтегруємо від 0 до R. Отримаємо внаслідок цього

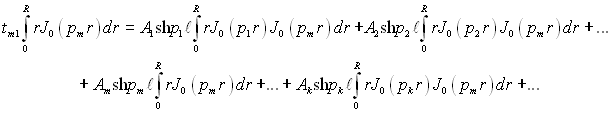(2.98)

При розрахунку параметра р з J₀(pr) = 0 виходить, що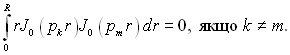

Ряд (2.98) внаслідок цього спрощується до

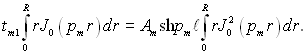(2.99)

В цьому рівнянні згідно пояснень до (2.70), 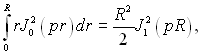якщо р визначається з rJ₀(pr) = 0. Із (2.99) знаходимо сталу інтегрування А_т:

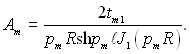(2.100)

Підставляючи (2.100) в (2.97), отримаємо формулу температурного поля в кінцевому вигляді:

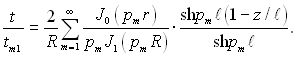(2.101)

Якщо, наприклад, температури на боковій поверхні і торцях суцільного циліндра будуть відрізнятися від нуля, розв’язок диференціального рівняння теплопровідності (2.81) необхідно шукати у вигляді суми:

t = u + υ + w,

де u – розв’язок задачі при u = t_n (r = R), u = 0 (z = 0) і u = 0 (z = ℓ); υ – розв’язок задачі при υ = 0 (r = R), υ = t_т1 (z = 0) і υ = 0 (z = ℓ) (аналіз яких виконаний вище); w – розв’язок задачі при w = 0 (r = R), w = 0 (z = 0) і w = t_m2 (z = ℓ).

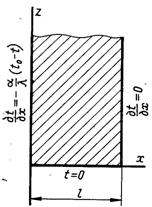
Рис.2.14. На половину обмежена плоска стінка

Нехай на одній з поверхонь (х = 0; 0 ≤ z < ∞) на половину обмеженої плоскої стінки (рис.2.14) теплообмін визначається граничними умовами ІІІ роду, 2-а поверхня (х = = ℓ; 0 ≤ z < ∞)  теплоізольована, а температура 3-ї поверхні (z = 0; 0 ≤ x ≤ ℓ)  дорівнює нулю.

Розв’язок диференціального рівняння (2.81) можна записати для цього випадку (п = 0 і ζ = х) так:

(2.102)

а граничні умови виразити наступним чином:

(2.103,а)

(2.103,б)

(2.103,в)

(2.103,г)

З граничної умови (2.103,г) слідує, що С₁ = 0, а підстановка цього рішення в (2.103,б) зводить його до виду:

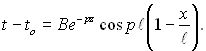 (2.104)

Якщо далі ввести (2.104) в рівняння (2.106,а), це дасть

 (2.105)

Із характеристичного рівняння (2.105) визначається параметр рℓ. Розв’язок (2.105) наведено в табл.2.2.

Таблиця 2.2. Корні характеристичного рівняння (2.105)

З табл.2.2 видно, що характеристичне рівняння (2.105) має множину коренів, отже рішення для t повинно мати вигляд:

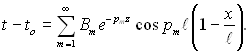(2.106)

Сталу В_т в (2.106) знаходимо за аналогічною методикою, яка використовувалася при визначенні А_т у формулі (2.90). Виходячи з цього, пропускаючи проміжні викладки, запишемо

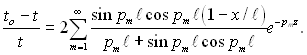(2.107)

Тепер замінимо граничну умову (2.103,б) на граничну умову І роду:

t = 0 при x = ℓ  (0 ≤ z ≤ ∞). (2.108)

У цьому випадку розв’язок диференціального рівняння (2.81) при п = 0 і ζ = х необхідно шукати у наступному виді:

t = u + υ, (2.109)

де u повинно задовольняти диференціальне рівняння

d²u/dx² = 0 (2.110)

і граничним умовам

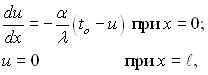(2.111)

а υ – диференціальне рівняння

д²υ/дх² + д²υ/ду² = 0 (2.112)

і граничним умовам

(2.113,а)

υ = 0           при х = ℓ,  0 ≤ z < ∞; (2.113,б)

υ = – u        при z = 0   0 ≤ x ≤ ℓ; (2.113,в)

дυ/дz = 0    при  z = ∞  0 ≤ x ≤ ℓ. (2.113,г)

Розв’язок диференціального рівняння (2.110) при граничних умовах (2.111) приводить до наступної формули:

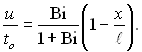(2.114)

Початкова функція від диференціального рівняння (2.112) має вигляд:

(2.115)

Із граничної умови (2.113,г) слідує, що С₂ = 0, а підстановка (2.115) послідовно в рівняння (2.113,б) і (2.113,а) дає

Таблиця 2.3. Корні характеристичного рівняння (2.117)

З (2.118) визначається стала D_m. Підставивши її в (2.115), отримаємо: