Розділ 3. НЕСТАЦІОНАРНІ ПРОЦЕСИ ТЕПЛОПРОВІДНОСТІ

3.1. Основні методи розв’язку рівняння нестаціонарного режиму теплопровідності

Диференціальне рівняння теплопровідності при відсутності внутрішніх джерел теплоти має вигляд

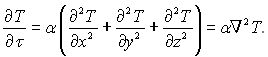(3.1)

Рівняння (3.1) – це лінійне однорідне диференціальне рівняння другого порядку в частинних похідних. Рішення такого рівняння володіють властивостями накладення, аналогічне рішенням звичайного однорідного диференціального рівняння другого порядку, для якого розв’язком є вираз С₁Т₁ + С₂Т₂, де Т₁ і Т₂ – окремі рішення рівняння, а С₁і С₂ – довільні сталі. У зв'язку з тим, що рівняння (3.1) є рівнянням в частинних похідних, то воно має безліч окремих рішень.

Диференціальне рівняння теплопровідності відноситься до так званих диференціальних рівнянь математичної фізики, для розв’язку яких напрацьовані як класичні методи, так і наближені. До класичних методів відносяться, наприклад, метод розподілу змінних, метод джерел і інтегрального перетворення. Широкого застосування набули наближені методи для любої задачі. До наближених методів відносяться метод кінцевих різниць (метод сіток) і метод аналогій (електроаналогія і гідроаналогія).

Метод розподілу змінних, запропонований Фур’є, для застосування до задач теплопровідності і полягає в тому, що знаходиться сукупність частинних рішень рівняння (3.1), які далі, про що вже говорилося, додаються:

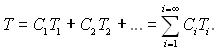(3.2)

Правомірність застосування принципу суперпозиції (накладення) для нескінченного ряду, так само як і можливість його почленного диференціювання і інтегрування, доказується в математичній фізиці. Суттєвим є обмеження функції T (T) для всіх значень координат і часу τ ≥ 0.

Розв’язок рівняння (3.1) подається у вигляді добутку двох функцій, одна з яких залежить тільки від часу T (τ), а інша φ(x, y, z) залежить тільки від координат, отже

T = СТ (τ)φ(x, y, z), (3.3)

де С – довільна стала.

Взявши похідні функції T за часом і координатам і підставивши в рівняння (3.1), отримаємо

T ′(τ)φ(x, y, z) = αТ(τ)Ñ²φ(x, y, z). (3.4)

Виконавши розподіл змінних, які залежать тільки від часу і тільки від координат, приведемо рівняння (3.4) до вигляду

T ′(τ)/Т(τ) = αÑ²φ(x, y, z)/φ(x, y, z) (3.5)

Ліва частина виразу (3.5) не залежить від координат, а права – від часу (при цьому рівність справедлива при любих значеннях часу і координат), то права і ліва частини представляють собою постійну величину λ:

(1/α) T ′(τ)/Т(τ) = λ; (3.6)

Ñ²φ(x, y, z)/φ(x, y, z) = λ. (3.7)

Кожне з рівнянь (3.6) і (3.7) є лінійним диференціальним рівнянням. Розв’язком рівняння (3.6) є

Т(τ) = Се^αλτ. (3.8)

Вигляд функції Т(τ) указує, що для процесів, прямуючих до теплової рівноваги, величина λ повинна бути меншою нуля (λ < 0), у протилежному випадку не буде виконуватися умова обмеженості функції T = Т (τ)φ(x, y, z) < М. Виходячи з цього можна позначити

λ = –k². (3.9)

У зв'язку з цим рівняння (3.7) набуває вигляду

Ñ²φ(x, y, z) + k²φ(x, y, z) = 0. (3.10)

Розв’язок рівняння (3.10), яке називається рівнянням Покеля, визначається геометричною формою тіла. Сталі інтегрування визначаються з граничних умов (температурою, тепловим потоком чи умовами теплообміну на поверхні тіла). У самому простому випадку, коли ? – функція тільки однієї координати (наприклад, х), рівняння (3.10) є звичайним диференціальним рівнянням другого порядку, розв’язок якого можна подати як суму двох окремих рішень:

φ(x) = С₁А (kx) + С₂B (kx), (3.11)

де С₁і С₂ – сталі величини, а А (kx) і B (kx) – лінійно незалежні інтеграли рівняння (3.10), іншими словами такі, відношення яких не є постійною величиною А (kx)/B (kx) ≠ const. Підставимо вирази (3.8) і (3.11) в (3.3) і об’єднавши сталі величини, отримаємо

(3.12)

де D і E – сталі величини.

Цей вираз, задовольняючи рівняння (3.1), але не годиться для розрахунку температурного поля, тому що з нього не можна визначити сталі D і E. Наприклад, якщо за умовою для початкового моменту часу (при ? = 0) температура постійна Т = Т₀ = const, то з рівняння (3.12) цього не слідує, тому що у цьому випадку оказується, що стала дорівнює змінній Т₀ = DA(kx)+EB(kx), чого не повинно бути. Виходячи з цього, для отримання загального рішення рівняння теплопровідності, яке задовольняє початкові умови, береться сума частинних рішень, в кожному з яких сталі D і E мають своє певне значення. Здійснюючи відповідний підбір значень D і E, можна як завгодно близько підійти до заданого початкового розподілу температури.

Таким чином, частинні рішення записуються так:

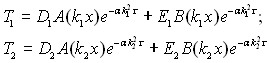(3.13)

і так далі.

Загальне рішення має вигляд

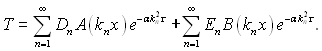(3.14)

Необхідною і достатньою умовою розв’язку задачі є можливість розкладення функції, яка описує початковий розподіл температури Т₀(х) у ряд за власними функціями:

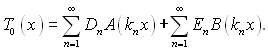
Застосування методу розподілу змінних наводиться нижче на прикладі нестаціонарного температурного поля плоскої пластини, циліндра, кулі.

Метод джерел є одним із класичних методів, особливо зручний при розв’язку задач теплопровідності для необмеженої чи на половину обмеженої області. Прикладом такої задачі може бути розгляд нестаціонарного температурного поля при зміні зовнішніх умов.

Фізична сутність метода джерел криється в тому, що процес розповсюдження теплоти в тілі теплопровідністю представляється як сукупність процесів вирівнювання температури від множини елементарних джерел теплоти, які розподілені як в просторі, так і в часі.

Розглянемо задачу по визначенню нестаціонарного одномірного температурного поля для необмеженої області при заданих початкових умовах. Фізичною моделлю такої задачі може служити стрижень безмежної довжини з постійною за довжиною площею поперечного перерізу F = 1 м², бокова поверхня якого теплоізольована. У стрижні задані початкові умови розподілу температур.

Для цієї задачі справедливе рівняння (3.1), тобто

Початковий розподіл температури у стрижні при τ = 0 Т(х, 0) = Т₀(х).

Як було показано раніше, метод розподілу змінних дозволяє отримати з рівняння (3.1) два звичайних лінійних диференціальних рівнянь, а саме:

Т′ + αk²Т = 0; φ″ +k²φ = 0 = 0.

Окремими рішеннями цих рівнянь є:

(3.15)

а окреме рішення (3.1) буде:

(3.16)

Функція Т(k) відповідає умові обмеженості. Тут k – довільне дійсне число ((–∞ < k < +∞), тому в рівнянні (3.16) береться знак плюс.

Утворюємо функцію:

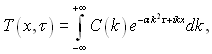(3.17)

яка задовольняє рівняння (3.1) як сума окремих рішень цього рівняння, якщо похідні можна розрахувати шляхом диференціювання під знаком інтеграла. Використовуючи початкові умови, отримаємо

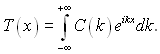(3.18)

Коефіцієнти С(k) знаходяться за формулою зворотного перетворення інтеграла Фур’є, тобто

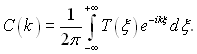(3.19)

Підставляючи (3.19) в (3.18) і змінюючи порядок інтегрування, отримаємо

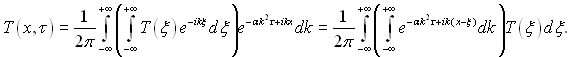(3.20)

Після перетворення інтеграл, що знаходиться в дужках, приводиться до наступного вигляду:

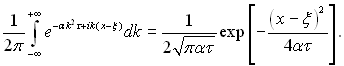(3.21)

Цей вираз називають фундаментальним розв’язком рівняння теплопровідності. Розв’язок називають також функцією джерела на нескінченності прямої і позначають

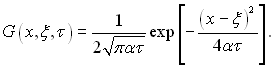(3.22)

З безпосередньої перевірки можна впевнитися, що функція

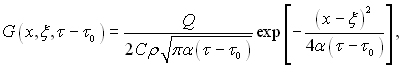(3.23)

Де С – теплоємність, ρ – густина матеріалу стрижня, яка являє собою температуру в точці х в момент часу τ, якщо у початковий момент часу τ = τ₀ у точці з координатою ξ виділяється кількість теплоти Q = Cρ (τ₀ можна приймати рівним нулю).

Дійсно, функція (3.23) задовольняє рівняння теплопровідності (3.1), тому що

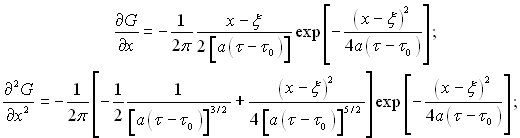
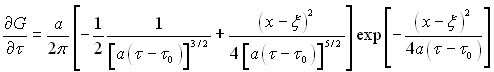
і, як наслідок

Кількість теплоти, яка знаходиться в стрижні в момент ? > ?₀,

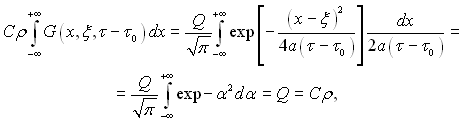(3.24)

тому що

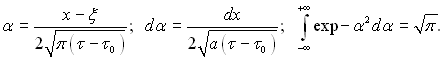
Як слідує з рівняння (3.24), кількість теплоти в стрижні не змінюється на протязі часу. Функція (3.23) залежить від часу тільки через ν = а(τ – τ₀), і її можна записати:

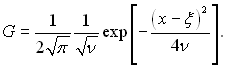(3.25)

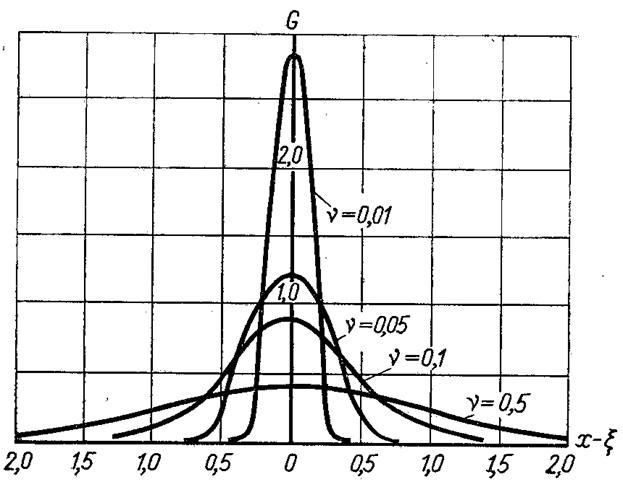
Рис.3.1. Вид функції G

Вид функції G представлений на рис.3.1, з якого слідує, що майже вся площа під кривою знаходиться над проміжком (ξ – ε) – (ξ + ε), де ε може бути дуже малим числом, якщо ν = а(τ – τ₀) досить мале. Величина площі, помножена на (Сρ), дорівнює кількості теплоти, що підводиться у початковий момент Для малих значень ν майже вся теплота знаходиться в малій зоні навколо точки ξ. Це значить, що в момент τ = τ₀ вся кількість теплоти знаходиться в точці ξ, а температура в точці при малих ? безмежно велика.

Доцільно відмітити наступне: формула (3.23) показує, що у довільній точці х температура, створювана миттєвим точковим джерелом теплоти, який діє в початковий момент τ = 0, відмінна від нуля для безмежно малих проміжок часу. Цей результат можна розглядати, як наслідок швидкого розповсюдження температури, а значить і теплоти. Але це знаходиться у протиріччі з молекулярно-кінетичним уявленням про природу теплоти. Невідповідність пояснюється застосуванням під час виводу диференціального рівняння теплопровідності феноменологічних уявлень про перенос теплоти, які не враховують інерційність руху молекул.

Повертаючись до виразу (3.20), запишемо його в наступному вигляді:

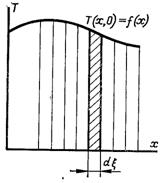
Рис.3.2. Початковий розподіл температури

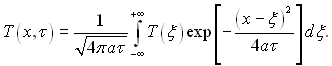(3.26)

Ця формула і є загальним розв’язком задачі визначення температурного поля в необмеженому одномірному тілі. Для початкового моменту часу рівняння (3.26) представляє собою заміну початкового розподілу температури сумою частинних рішень (рис.3.2).

Методи інтегрального перетворення. Для розв’язку багатьох задач теплопровідності класичні методи оказуються недостатніми, в зв'язку з чим знаходять широке застосування різні методи інтегральних перетворень диференціальних рівнянь і граничних умов. Сутність метода інтегральних перетворень криється в тому, що вивчаються не самі функції, які визначаються постановкою задачі, а їх видозмінення – так назване зображення; сама ж функція називається оригіналом. Якщо перетворення береться за просторовою координатою х, то інтегральне перетворення функції оригіналу f(x) може бути представлена в наступному вигляді:

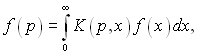(3.27)

де f(р) – зображення функції f(x); К(р, х) – ядро перетворення; р – певний параметр.

Межі інтегрування можуть бути як нескінченними, так і кінцевими, в останньому випадку інтегральне перетворення називається кінцевим і має вид

Вигляд ядра перетворення визначається умовами розглядуваної задачі. Так, для тіл необмеженої протяжності зручно застосовувати комплексне перетворення Фур’є, для якого і межі інтегрування в рівнянні беруться від –∞ до +∞.

Якщо задані на поверхні тіла граничні умови І роду (задано значення функції) варто використовувати синус-перетворенням Фур’є, при граничних умовах ІІ роду косинус-перетворенням Фур’є. При цьому ядра перетворень відповідно мають вигляд:

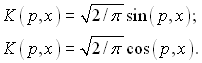(3.28)

Для тіл з осьовою симетрією (наприклад, для циліндра) ядром перетворення повинна бути функція Бесселя

К(р, х) = rJ(pr), (3.29)

де J(pr) – функція Бесселя; r – незалежна змінна, яка змінюється від 0 до R (R – зовнішній радіус). Інтегральне перетворення в цьому випадку носить назву перетворення Ханкеля.

При вирішенні задач нестаціонарної теплопровідності найбільше розповсюдження отримали метод інтегрального перетворення Лапласа і операційний метод Хевісайда. У цьому методі інтегральне перетворення функції, який залежить від часу f(τ), визначається функцією

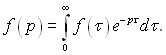(3.30)

Застосування метода інтегральних перетворень до диференціальних рівнянь в частинних похідних дозволяє отримати для одномірного випадку звичайне диференціальне рівняння відносно зображення. Застосування інтегрального перетворення до звичайних диференціальних рівнянь переводить їх в алгебраїчне відносно зображень. Знаходження після значення функції, є зображенням, необхідним (для вирішення задачі) для переходу до оригіналу. Цей перехід здійснюється за формулами повернення:

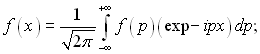для комплексного перетворення Фур’є

(3.31)

для синус-перетворення Фур’є

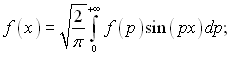(3.32)

для косинус-перетворення Фур’є

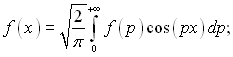(3.33)

для перетворення Ханкеля

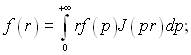(3.34)

для перетворення Лапласа

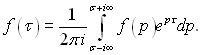(3.35)

У зв'язку з широким застосуванням операційного метода розглянемо його більш докладніше.

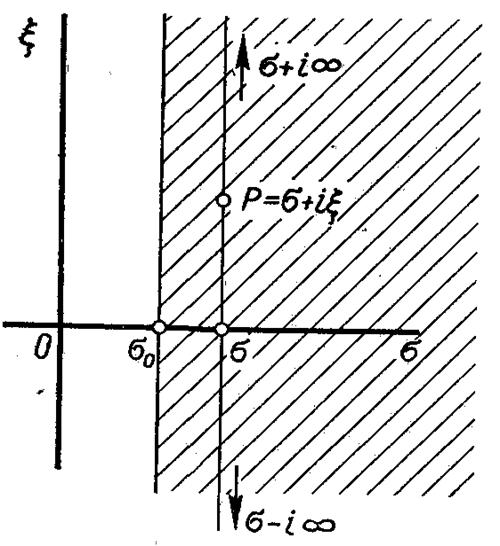
Рис.3.3. Область існування зображення f(p) функції f(τ)

Перетворення Лапласа здійснюється у відповідності з формулою (3.30), де параметр р = σ + іξ є деякою комплексною величиною, яка при сталому значенні σ і змінному ξ в межах від –∞ до +∞, змінюється від σ – і∞ до σ + і∞ (рис.3.3), проходячи у комплексній області р пряму Re(p) = σ, паралельну уявній осі. Перетворенню Лапласа підлягають функції з наступними властивостями:

1. При від’ємних значеннях аргументу відповідна функція дорівнює нулю:

f(τ) = 0 при τ < 0.

2. При додатних значеннях аргументу порядок зростання абсолютних значень функції при збільшенні аргументу не перевищує порядку зростання деякої показникової функції:

Так, наприклад, функція ехр τ² не має зображення, тому що інтеграл Лапласа розходиться.

3. Функція f(τ) повинна задовольняти умови Дірихле, це значить що інтервал, на якому визначена функція f(τ), може бути розбита на кінцеву кількість інтервалів, в кожному з яких f(τ) безперервна і монотонна, і в довільній точці розриву значення функції f(τ + 0) і f(τ – 0) існує.

При названих обмеженнях зображення f(р) є аналітичною функцією в правій напівплощині від прямої Re(p) = σ₀(рис.3.3), тобто функція f(р) має похідні всіх порядків в названій області і всі її особливі точки розташовані в комплексній області зліва від прямої σ₀.

Знайти зображення:

1.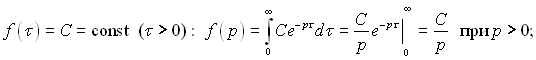 (3.36)

2. 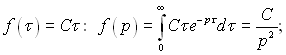(3.37)

3. 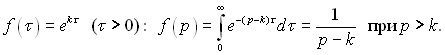(3.38)

Якщо f(τ) = е^–kτ, то f(р) = 1/(р + k) (3.39)

Основні властивості перетворень Лапласа.

Лінійність. З приведених прикладів виходить, якщо величина С = const і оригіналу f(τ) відповідає зображення f(р), то функція Сf(τ) відповідає зображенню Сf(р). Далі, якщо функції f₁(τ) і f₂(τ) мають відповідно зображення f₁(р) і f₂(р), то справедлива рівність

f₁(τ) + f₂(τ) = f₁(р) + f₂(р), (3.40)

тобто зображення суми оригіналів дорівнює сумі зображень цих оригіналів. Наприклад,

тоді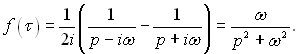

Для випадку

зображення має наступний вигляд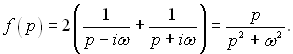

Зображення похідної. Якщо φ(τ) = f '(τ), то, використовуючи правило інтегрування по частинам, отримаємо 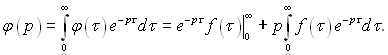(3.41)

Якщо f (τ) належить до функцій з властивостями 1, 2, 3, то е^–рτf(τ)→0 при τ→∞ і е^–рτf(τ)→f(0) при τ→0. У цьому разі вираз (3.41) приводиться до вигляду

φ(р) – f '(р) = рf (р) – f(0), (3.42)

тобто диференціювання оригіналу функції відповідає добутку зображення на р з наступним визначенням сталої f(0). Для похідної другого порядку ψ(τ) = f"(τ)

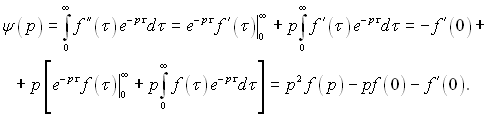(3.43)

У загальному випадку, якщо F(τ) = f⁽ⁿ⁾(τ), зображення цієї функції визначається за формулою:

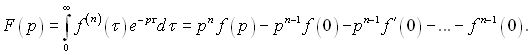(3.44)

Щоб відшукати початкову функцію оригіналу за її зображенням можна користуватися формулою (3.35). Методика інтегрування в комплексній площині викладена в теорії функцій комплексної змінної. Але частіше користуються готовими таблицями для оригіналів і зображень, крім цього замість формули (3.35) використовують функцію перетворення (знаходження оригіналу за зображенням):

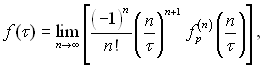(3.45)

де f(p) – зображення функції f(τ), в яку замість величини р підставляється (п/τ), наприклад f(p) = 1/(р +1). Необхідно знайти f(τ). Тому що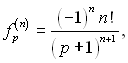

то у відповідності з (3.45)

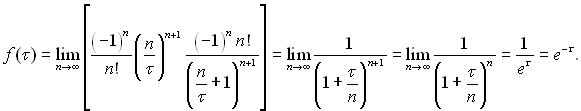(3.46)

Формула (3.45) дає можливість визначати оригінал тільки за допомогою диференціювання з подальшим переходом до границі. Для ілюстрації застосування перетворення Лапласа розглянемо перетворення одномірного диференціального рівняння теплопровідності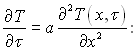

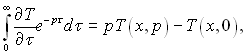(3.47)

де Т(х, р) – зображення оригіналу Т(х, τ); Т(х, 0) – початковий розподіл температури:

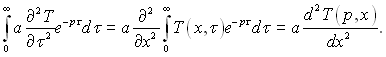(3.48)

Таким чином, рівняння (3.1) в частинних похідних перетворюється в звичайне диференціальне рівняння відносно зображення:

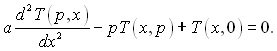(3.49)

Розглянемо найпростіший випадок, коли початковий розподіл температури однаковий для всіх точок тіла і рівний нулю:

Т(х, 0) = 0. (3.50)

Тоді рівняння (3.49) набуває вигляду

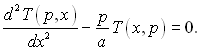(3.51)

Розв’язок цього рівняння дає:

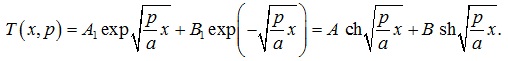(3.52)

де А₁ = (А + В) / 2 і В₁ = (А – В) / 2 – величини постійні відносно х, але залежать від р. Ці сталі величини визначаються з граничних умов, після чого за допомогою таблиць зображень знаходиться оригінал Т(х, τ).