




3.2. Нестаціонарні процеси теплопровідності в необмеженій пластині
Розглянемо задачу, коли тепло прямує до теплової рівноваги. При цьому задана пластина товщиною 2δ, розміри у напрямку осей у і z необмежені (рис.3.4).
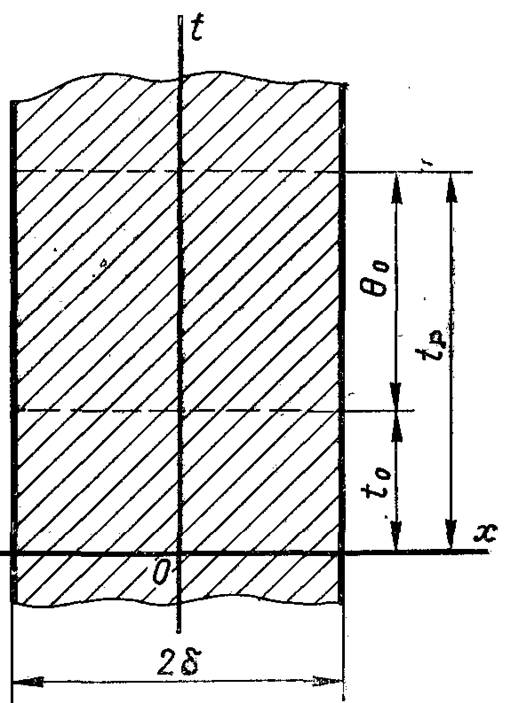
Рис.3.4. Схема до розрахунку нагрівання плоскої пластини
Фізичні умови визначають значення коефіцієнта теплопровідності матеріалу пластини (λ = const), теплоємності (С = const), густини ρ, внутрішні теплові джерела відсутні. Пластина, яка мала в початковий момент часу однакову температуру t0 занурюється в потік рідини зі сталою температурою tр, відмінною від t0.
Граничні умови визначені усталеними й однаковими значеннями коефіцієнтів тепловіддачі α на обох поверхнях пластини.
У зв'язку з тим, що лінійні розміри поверхні пластини великі у порівнянні з її товщиною, зміна температури буде відбуватися тільки у напрямку, перпендикулярному до поверхні пластини, тобто температурне поле буде одномірним. Крім цього, із-за симетричності граничних умов відносно середньої площини температурне поле в довільний момент часу буде також симетричним відносно цієї площини. Для розглядуваної задачі початок координат зручно розміщати в центрі пластини, як показано на рис.3.4, спрямувавши ось Ох по нормалі до осі пластини. Для зручності наступних розрахунків відлік температури ведеться від температури навколишнього середовища J = tp – t.
Тоді диференціальне рівняння теплопровідності (3.1) запишеться так:
![]() (3.53)
(3.53)
тому що
![]() (3.54)
(3.54)
Умови однозначності приймають вигляд:
Останнє рівняння можна замінити більш простою умовою симетрії температурного поля:
дJ/дх = 0 при х = 0. (3.57)
Розв’язуємо поставлену задачу методом розділу змінних, подаючи шукану функцію J у вигляді добутку двох функцій φ(х) і Т(τ), кожна з яких залежить тільки від одного аргументу
J = φ(х)Т(τ). (3.58)
Підставляючи (3.58) в (3.53), отримаємо
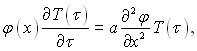 (3.59)
(3.59)
чи розділяючи перемінні,
![]() (3.60)
(3.60)
Тому що
ліва частина рівняння (3.60) не залежить від координати х, а права – від
часу τ, то загальне значення і правої і лівої частин не повинно залежати
ні від х, ні від τ:
![]() (3.61)
(3.61)
З умови
(3.55) виходить, що при нагріванні пластини дJ/дτ
≤
0 (це значить, що дТ/дτ <0), тоді константа в рівнянні (3.61) повинна
бути від’ємною. (У випадку охолодження пластини при
tp
>
t0
вивід
відносно знаку константи буде таким самим).
Позначимо константу через (–k2) і, розв’язуючи рівняння (3.61), отримаємо:
![]() (3.62)
(3.62)
![]() (3.63)
(3.63)
де С1, С2, С3 – сталі інтегрування, які так само як і значення сталої k, знаходяться з початкових і граничних умов.
Використовуючи умови симетрії (3.57) ![]() маємо
маємо
![]() (3.64)
(3.64)
Виконавши диференціювання (3.63) з урахуванням (3.64), знаходимо С2=0, тоді
![]() (3.65)
(3.65)
Вираз для поля надлишкової температури має вигляд
![]() (3.66)
(3.66)
де С = С1С3.
Використовуючи граничну умову (3.56) у виді
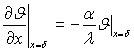 (3.67)
(3.67)
отримуємо при підстановці рівняння (3.66) і похідної дJ/дх при значенні х = ?
![]() (3.68)
(3.68)
чи після скорочення лівої і правої частини рівняння, отримуємо трансцендентальне рівняння для визначення сталої k:
![]() (3.69)
(3.69)
чи
![]() (3.70)
(3.70)
Позначивши kδ = n і αδ/λ =Ві (число Біо), отримаємо:
п/Ві = ctg(n). (3.71)
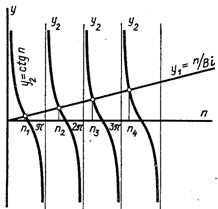
Рис.3.5. Розв’язок рівняння (3.71)
Рівняння (3.71) називається характери-тичним рівнянням; його можна розв’язати графічним способом, знаходячи точки перетину прямої у1 = п/Ві з котангенсоїдами у2 = ctg(п). На рис.3.5 наведена схема графічного розв’язку рівняння (3.71). Як видно з рисунка, рівняння (3.71) має безліч рішень пi; ці значення називаються власними числами задачі. Величини власних чисел залежать від порядкового номера і і числа Ві. Характер цієї залежності наведено на рис.3.6.
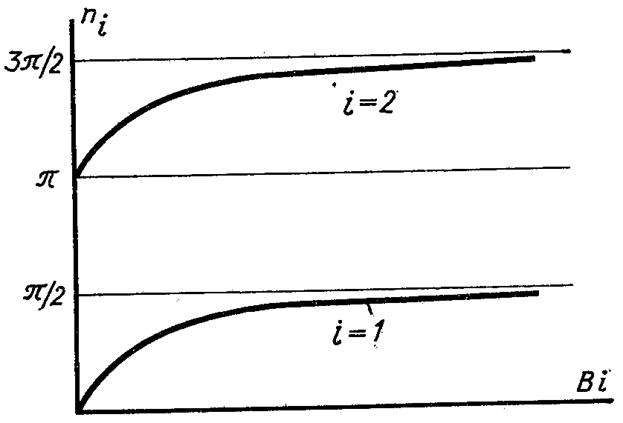
Рис.3.6. До визначення власних чисел пі
При Ві→∞ пряма у1 = п/Ві співпадає з віссю абсцис і корні рівняння (3.71) мають значення:
При Ві→0 пряма у1 = п/Ві співпадає з віссю ординат і власні числа стають рівними:
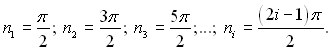
де і = 1, 2, 3.
Таким чином, виходячи з рівняння (3.66) кожне значення власного числа пі приводиться до окремого рішення:
![]() (3.72)
(3.72)
Загальний розв’язок диференціального рівняння (3.53) визначається сумою окремих рішень:
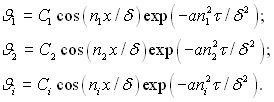 (3.73)
(3.73)
Функція J задовольняє граничні умови, тому що їм відповідають усі члени ряду. Сталі Сі визначаються з початкових умов (3.55):
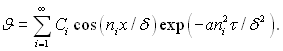 (3.74)
(3.74)
це значить, що Сі є коефіцієнтами Фур’є функції J0 при розкладанні її за косинусами в інтервалі від –δ до +δ.
Для визначення коефіцієнтів Сі права і ліва частини рівняння (3.74) множаться на cos(njx/δ)dx і інтегруються від –δ до +δ, а j приймає всі цілі значення, включаючи і число і:
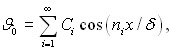 (3.75)
(3.75)
Неважко показати (властивість ортогональності), що
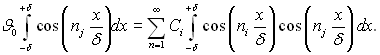 (3.76)
(3.76)
Внаслідок цього вираз для визначення Сі набуває наступного виду:
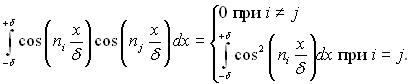 (3.77)
(3.77)
Підставляючи отримане рівняння (3.77) в (3.73), отримаємо кінцевий вираз для температурного поля симетричної однорідної пластини, яка нагрівається:
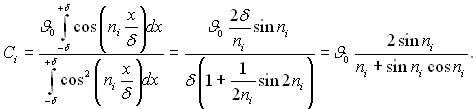 (3.78)
(3.78)
Беручи до уваги, що аτ/δ2 = Fo – число Фур’є, запишемо вираз для безрозмірного перепаду температури:
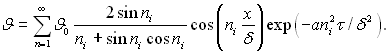 (3.79)
(3.79)
У більшості практичних задач необхідно визначати температуру в характерних
точках тіл. Так, для пластини найбільший інтерес представляє визначення
температури чи на поверхні х = ±δ, чи в середній площині х
= 0. Для цих випадків безрозмірна координата х( = х/δ приймає
значення чи 1, чи 0. Вираз 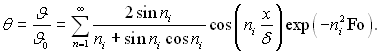 є
функцією тільки пі, тобто функцією порядкового номера і числа
Ві. Тому що пі – числа, величина яких зростає з порядковим
номером, то наступні члени ряду відіграють все меншу роль зі зростанням пі
[варто пам’ятати, що cos (ni х( ) – величина обмежена, а ехр(–пі2Fo)
– величина, що швидко зменшується].
є
функцією тільки пі, тобто функцією порядкового номера і числа
Ві. Тому що пі – числа, величина яких зростає з порядковим
номером, то наступні члени ряду відіграють все меншу роль зі зростанням пі
[варто пам’ятати, що cos (ni х( ) – величина обмежена, а ехр(–пі2Fo)
– величина, що швидко зменшується].
Дослідження показують, що при Fo ≥ 0,3 ряд (3.79) стає швидкозбіжним і може з достатньою точністю замінений першим членом ряду:
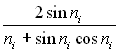 (3.80)
(3.80)
Для осі пластини (х( = 0) маємо
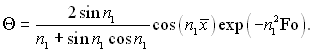 (3.81)
(3.81)
для зовнішньої поверхні (х( = 0) маємо
![]() (3.82)
(3.82)
де N(Bi) і Р(Ві) – функції, що залежать тільки від числа Біо.
![]()

Рис.3.7. Залежність безрозмірного перепаду температур від чисел Фур’є і Біо
для поверхні пластини
Таким чином, при заданих координатах безрозмірний перепад температур є функцією тільки двох чисел: Ві і Fo. Виконуючи логарифмування рівнянь (3.81) і (3.82), отримуємо вирази:
(3.83)
Рівняння (3.83) зручно представити в напівлогарифмічних координатах (рис 3.7
і 3.8) По осі ординат відкладені натуральні логарифми величини ![]() чи
чи ![]() , а
по осі абсцис – число Фур’є.
, а
по осі абсцис – число Фур’є.
![]()

Рис.3.8.Залежність безрозмірного перепаду температур від чисел Фур’є і Біо
для середини пластини
Число Біо використовується як параметр. Користуючись графіками, можна виконувати наступні розрахунки:
З рівняння (3.79) виходить, що температурне поле в пластині має для довільного моменту часу вид симетричної кривої [cos (ni х( ) – парна функція]. Мінімум кривої знаходиться на осі пластини.
Для довільного моменту часу дотичні до температурних кривих в точках х(
= ±1 проходять через одні і ті ж симетрично розташовані точки ±N
(рис.3.9). Ці точки називаються направляючими і знаходяться від поверхні
пластини на відносній відстані х( = 1/Ві. Для доведення цього твердження
перетворимо граничні умови (3.67)![]()
до безрозмірного виду, помноживши обидві частини рівності на ?/J0
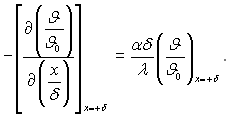 (3.84)
(3.84)
Тоді рівняння (3.84) запишеться так:
![]() (3.85)
(3.85)
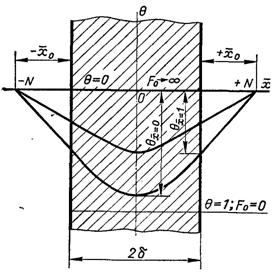
Рис.3.9. Зміна температурного поля необмеженої пластини
Згідно схеми рис.3.9,
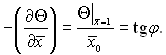 (3.86)
(3.86)
З порівняння рівнянь (3.85) і (3.86) виходить
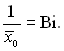 (3.87)
(3.87)
Підставляючи в рівняння (3.87) розмірні величини, знайдемо, що
![]() (3.88)
(3.88)
тобто відстань точки N від поверхні пластини визначається умовами однозначності, і дотичні до всіх температурних кривих в точці перетину їх з поверхнею пластини за незмінних умов однозначності завжди проходять через точку N.
3.3. Кількість теплоти, що сприймається пластиною під час нагрівання
Кількість теплоти, що надходить в пластину з обох сторін за час від τ = 0 до τ = ∞, дорівнює зміні ентальпії за цей проміжок часу (температура пластини у всіх точках досягає температури рідини):
![]() (3.89)
(3.89)
де t0 – температура пластини в початковий момент часу.
За довільний проміжок часу від 0 до τ1 ентальпія змінюється на
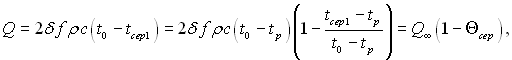 (3.90)
(3.90)
де 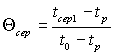 – середній безрозмірний перепад температури в момент часу
τ1,
tсер1 – середня температура по товщині пластини в
момент часу
τ1.
– середній безрозмірний перепад температури в момент часу
τ1,
tсер1 – середня температура по товщині пластини в
момент часу
τ1.
Величину τсер у відповідності до теореми про середнє можна визначити з виразу
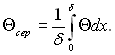 (3.91)
(3.91)
Підставляючи значення ? з рівняння (3.79), після інтегрування матимемо:
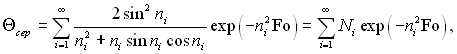 (3.92)
(3.92)
де Ni – коефіцієнт, що залежить від Ві.
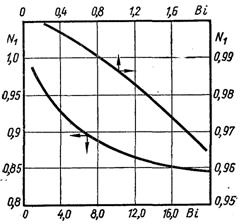
Рис.3.10. До визначення величини Ni
При значеннях числа Fo ? 0,3 (3.92) стає швидкозбіжним і для розв’язку практичних задач обмежуються першим членом ряду:
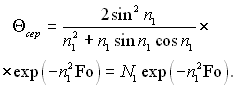 (3.93)
(3.93)
Значення коефіцієнта Ni приведені на рис.3.10.
3.4. Вплив чисел Біо і Фур’є на температурне поле в пластині
При великих значеннях чисел Біо (Ві→ ∞) власні числа приймають значення 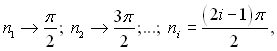 (див.
рис.3.6):
при цьому
(див.
рис.3.6):
при цьому ![]()
За цих умов рівняння (3.79) приймає наступний вид:
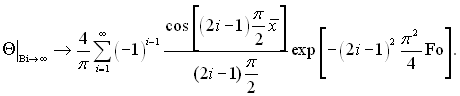
З цього виразу виходить, що для поверхні пластини (х( = 1)
![]() (3.94)
(3.94)
Розподіл температури в інших точках пластини залежить від співвідношення внутрішнього і зовнішнього термічних опорів. якщо ?/? >> 1/?, то температура поверхні з самого початку процесу стає рівною температурі гріючої рідини tр, тоді граничні умови ІІІ роду переходять в умови І роду. При ?/? << 1/? мають місце малі значення числа Біо (Ві ? 0). За цієї умови п1? 0; п2? ?;...; пі? (і – 1)? і тоді з рівняння (3.77) слідує, що:
і тобто температура за товщиною пластини в довільний момент часу оказується однаковою і постійною.
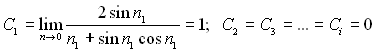
![]()
? 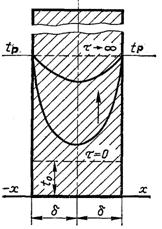
Рис.3.11. Зміна температурного поля в необмеженій пластині при великих числах Біо
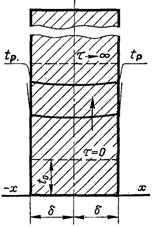
Рис.3.12. Зміна температурного поля в необмеженій пластині при малих числах Біо ?
При Ві > 0, але значно менше одиниці, tg п1 ≈ п1 і з трансцендентного рівняння п1/Ві = 1/tg п1 слідує, що п1 ≈ Ві0,5. Тому при Ві << 1
![]() (3.95)
(3.95)
зміна поля температури відбувається в основному в часі.
На рис.3.11 і 3.12 представлений характер зміни температурного поля для різних випадків зміни числа Ві. Виконані розрахунки показують, що зміна температурного поля, подані на рис.3.11, має місце при Ві ≥ 100, а умова Ві <<1 виконується практично при Ві ≤ 0,1 (рис.3.12).
Вплив числа Фур’є (Fo) проявляється на полі температур наступним чином: при зменшенні Fo збіжність ряду в рівнянні (3.79) покращується. Як уже говорилося, для значення Fo ? 0,3 ряд можна замінити його першим членом (3.80):
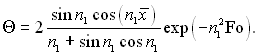 (3.96)
(3.96)
Область виродження формули (3.79) і (3.80) називається регулярним температурним режимом, при цьому поле перепаду температур залишається подібним самому собі у всі послідуючі моменти часу. Такий процес називається автомодельним у часі.
3.5. Теплопровідність у тілах, утворених перерізом пластин
Такі тіла, як прямокутні бруски, паралелепіпеди, можна розглядати як результат перерізу двох чи трьох взаємно перпендикулярних пластин, які мають такі самі умови однозначності, що і відповідні їм поверхні розглядуваного тіла.
Розглянемо температурне поле прямокутного бруска, який складається з однорідного ізотропного матеріалу. Брус являє собою переріз двох необмежених пластин. Нестаціонарне поле надлишкових температур при нагріванні бруса підпорядковується рівнянню Фур’є
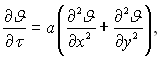 (3.97)
(3.97)
де J = tp – t.
Початкові і граничні умови для пластин приймаються однаковими для
–δх ≤ х ≤ +δх;
–δу ≤ у ≤ +δу;
J = J0 = tp – t0 при τ = 0;
J = 0 при τ → ∞;(3.98)
λдJ/дх+αJ
= 0
при х = δх;
(3.99)
дJ/дх = 0 при х = 0, –δу ≤ у ≤ +δу;
дJ/ду = 0 при у = 0, –δх ≤ х ≤ +δх.(3.100)
Докажемо, що безрозмірний перепад температур бруса дорівнює добутку безрозмірних перепадів температур в пластинах:
Θ = Θх · Θу (3.101)
де
![]() (3.102)
(3.102)
![]() (3.103)
(3.103)
Перепишемо вираз (3.101) в такому виді:
J = JхJу/J0. (3.104)
Підставляючи останнє рівняння (3.104) в (3.97), отримаємо
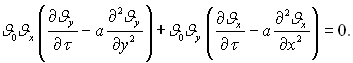 (3.105)
(3.105)
Рівність нулю всього виразу слідує з рівності нулю виразів в дужках, тому
Jх і Jу є розв’язками відповідних диференціальних рівнянь для пластини:
JхJу/J0 = 0 при τ → ∞, тому що Jх→ 0 і Jу→ 0 при τ → ∞;
при 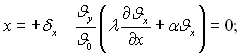 (3.106)
(3.106)
при 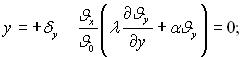 (3.107)
(3.107)
при х = 0; 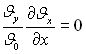 (3.108)
(3.108)
при у = 0.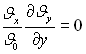 (3.109)
(3.109)
Останнє справедливо, оскільки похідні дорівнюють нулю внаслідок симетрії температурного поля у кожній окремо розглядуваній пластині.
Таким чином, вираз (3.101) задовольняє диференціальне рівняння, початкові і граничні умови и, як наслідок, є розв’язком задачі.
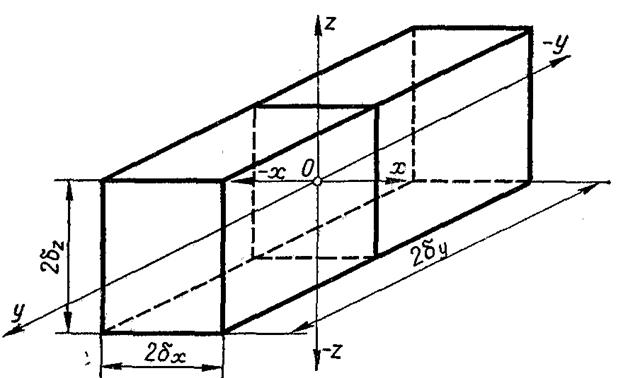
Рис.3.13. Схема до розрахунку температурного поля паралелепіпеда
Аналогічний результат можна отримати при розгляді температурного поля паралелепіпеда (рис.3.13), для якого безрозмірний перепад запишеться так:
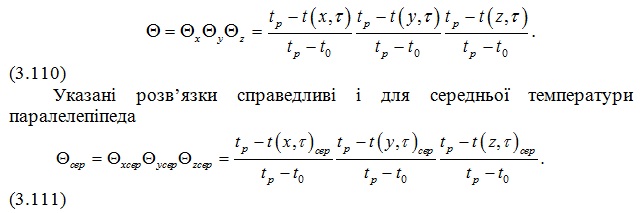
При визначенні температури в характерних точках – центра паралелепіпеда, центра граней – можна використати наведені раніше графіки (див. рис.3.7 і 3.8) для знаходження ?х, ?у, ?z.
Наведений приклад розв’язку задачі для тіл кінцевих розмірів можна застосувати і для визначення температурного поля в циліндрі кінцевої довжини, який являє собою тіло, отримане внаслідок перерізу необмежених циліндра і пластини.