3.6. Температурне поле пластини з внутрішніми джерелами теплоти

Розглянемо задачу, яка відрізняється від розглянутої вище тим, що на пластині рівномірно розташовані джерела теплоти з постійною потужністю q_V, Вт/м³. Поле температур підпорядковане диференціальному рівнянню

(3.112)

Пластина знаходиться в рідині з температурою t_p і в початковий момент має ту саму температуру, що і рідина. В початковий момент в пластині починають діяти джерела теплоти. Початкові і граничні умови мають вид

                                  при τ = 0  t = t_p   –δ ≤ х ≤ +δ;                                  (3.113)

                             –λдt/дх=α(t – t_p) = 0   при х = +δ;                              (3.114)

                          дt/дх= 0   при х = 0  (умова симетрії).                         (3.115)

Для розв’язку задачі зручно перетворити наведені рівняння, вводячи надлишкову температуру J = t_∞ – t, яка являє собою різницю між температурою стаціонарного поля (така, що настає після тривалого проміжку часу) і нестаціонарною температурою.

Стаціонарний розподіл температури визначається за формулою:

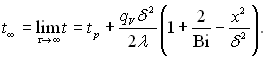(3.116)

Таке стаціонарне поле підпорядковане наступним диференціальному рівнянню і граничним умовам:

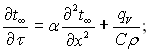(3.117)

(3.118)

(3.119)

Віднімаючи рівняння (3.117), (3.118), (3.119) відповідно з (3.112), (3.114), (3.115), а рівняння (3.116) – з (3.113), отримаємо:

(3.120)

(3.121)

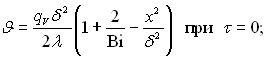(3.122)

(3.123)

Отриману систему (3.120)...(3.123) розв’язуємо методом розділення перемінних і отримуємо загальне розрахункове рівняння

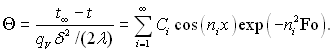(3.124)

де власні числа п_і визначаються з уже відомого трансцендентального рівняння (3.71), а коефіцієнти

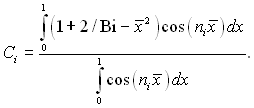(3.125)

3.7. Нестаціонарне температурне поле безмежно довгого циліндра

Розглянемо задачу з визначення температурного поля в безмежному циліндрі радіуса R₀, початкова температура якого t₀. Циліндр знаходиться в середовищі зі сталою температурою t_p > t₀; коефіцієнт тепловіддачі ? у всіх точках зовнішньої поверхні циліндра залишається постійним на протязі всього часу нагрівання; у зв'язку з цим ізотермічне температурне поле залежить від радіуса і часу.

Диференціальне рівняння для розглядуваної задачі

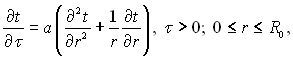(3.126)

умови однозначності при τ = 0, t = t₀, 0 ≤ r ≤ R₀;;

(3.127)

(3.128)

з умови симетрії t_r=0 ≠ ∞, , тобто в центрі циліндра температура має кінцеве значення.

Після заміни перемінних (вважаючи, що J = t_p – t) система рівнянь, яка описує температурне поле безмежного циліндра, перетворюється до виду

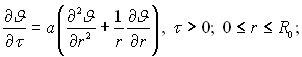(3.129)

(3.130)

(3.131)

(3.132)

Для розв’язку застосуємо метод розділу перемінних, який, як і випадку безмежної пластини, приводить до окремого рішення виду

(3.133)

У цьому рівнянні ?(r) є розв’язком рівняння Бесселя

(3.134)

Тому що ? залежить тільки від радіуса r, то загальний розв’язок рівняння (3.134) представимо сумою двох окремих рішень:

                                                            ψ = φ(r) + μ(r).                                       . (3.135)

Це слідує з того, що загальний розв’язок любого лінійного однорідного диференціального рівняння другого порядку виду

                                                     у″ + р(х)у′ + q(x)y = 0,                                          (а)

до якого відноситься і рівняння (3.134), можна записати так:

у = С₁у₁ + С₂y₂,... (б)

де С₁ і С₂ – постійні; у₁ і y₂ – лінійні незалежні рішення рівняння (а), тобто у₁/ y₂ ? const.

При цьому достатньо знати тільки одне лінійно незалежне вирішення, наприклад у₁, тоді друге визначається з формули

(в)

Перше окреме вирішення – φ(r) – визначається з перетворення рівняння Бесселя (3.134):

                                     rφ″(r) + φ′(r) + k²φ(r) = 0                                    (3.136)

чи, замінюючи r = x/k і враховуючи, що в цьому випадку φ″(r) = k²φ″(x);         φ′(r) = kφ′(x), отримаємо рівняння

                                                      xφ″ + φ′ + xφ = 0.                                          (3.137)

Розв’язок цього рівняння відшуковується у вигляді степеневого ряду

                                   φ = а₀ + а₁х + а₂х² + а₃х³ + ...                                 (3.138)

Диференціюємо почленно (3.138):

                                φ′ = а₁ + 2а₂х + 3а₃х² + 4а₄х³ + ...                             (3.139)

                            φ″ = а₁ + 2·1а₂ + 3·2а₃х + 4·3а₄х² + ...                          (3.140)

Підставляючи (3.138), (3.139), (3.140) в (3.137) і групуючи члени з однаковими степенями біля х, отримаємо

                            а₁ + (а₀ + 2²а₂)х + (а₁ + 3²а₃)х² + (а₂ + 4²а₄) х³ + ...               (3.141)

Вираз (3.141) дорівнює нулю за умови, що а₁ = 0; а₀ + 2²а₂ = 0; а₁ + 3²а₃ = 0; ...; а_п–2 + а_пп² = 0. З цих рівнянь виходить, що всі коефіцієнти з непарними індексами дорівнюють нулю, а коефіцієнти з парними індексами виражаються через а₀: а₂ = –а₀/2²; а₄ = –а₀/2²·4²; а₆ = –а₀/2²·4²·6²; ...;  а_2п = –а₀/(2п)²!. Внаслідок цього, окреме рішення φ(х) являє собою:

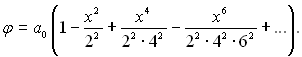(3.142)

Якщо прийняти, що а₀ = 1, то окремий інтеграл рівняння (3.137) становить наступну функцію

(3.143)

яка називається функцією Бесселя І роду нульового порядку.

Для знаходження другого окремого рішення використаємо формулу (в)

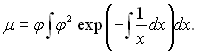
Підставляючи в цей вираз значення ? і виконуючи розрахунки, отримаємо

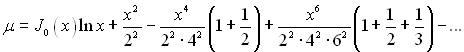(3.144)

Для зручності розрахунків замість функції μ до загального рішення (3.135) підставляється функція Y₀(x) зв’язана з μ співвідношенням

(3.145)

де С = 0,577 – стала Ейлера, Y₀(x) – функція Бесселя ІІ роду нульового порядку.

Вид функції J₀(x) і Y₀(x) наведено на рис.3.14.

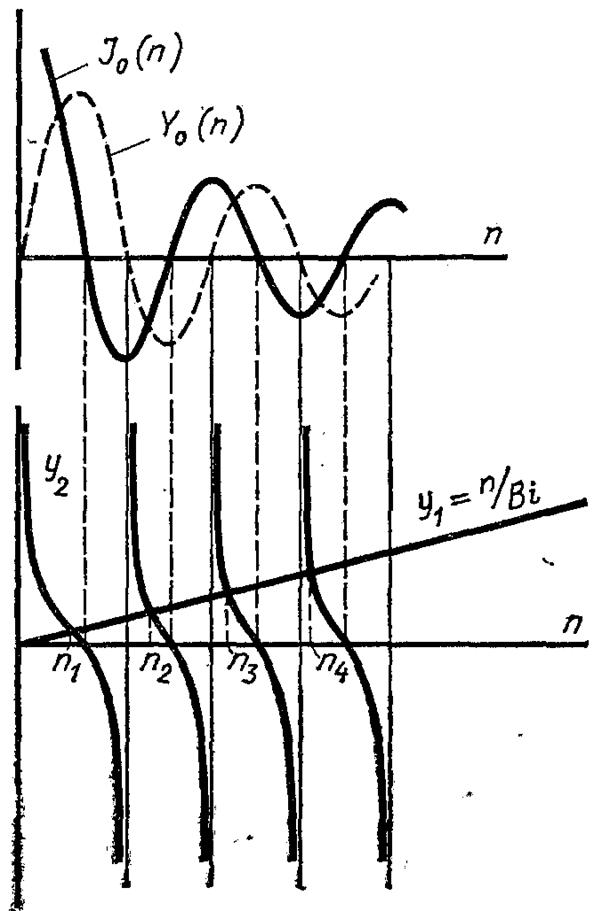
Рис.3.14. До розв’язку рівняння (3.150)

Окремі рішення J₀(x) і Y₀(x) лінійно незалежні, загальний інтеграл рівняння (3.134) має наступний вигляд:

(3.146)

чи, повертаючись до змінної r (x = kr),

(3.147)

Тому що температура на осі циліндра (r = 0) повинна бути кінцевою, то рішення (3.147) не повинно містити в собі функцію Y₀, яка прямує до нескінченності при r → 0, тоді С₂ = 0 і рішення (3.147) приймає вид

(3.148)

Сталі k і С визначаються з граничних і початкових умов.

Попередньо відмітимо, що

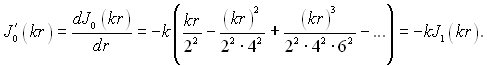(3.149)

У цьому рівнянні J₁(kr) – функція Бесселя І роду першого порядку. Задовольняємо рішення (3.148) граничними умовами

Скоротимо вираз на отримаємо

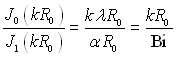. (3.150)

Трансцендентальне рівняння (3.150) розв’язується графічним шляхом. Позначимо

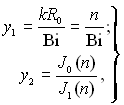(3.151)

де kR₀ = n.

Графік функції y₂ = J₀(n)/J₁(n) нагадує котангенсоїду, але зі спадним періодом, графік функції у₁ – пряма лінія, яка проходить через початок координат. На рис.3.14 наведений графічний спосіб визначення корнів рівняння (3.150). Як видно з наведеного графіка, що існує безмежна множина корнів n_i, які визначаються перетином графіків функцій у₁ і у₂. Загальний розв’язок є сума всіх окремих рішень:

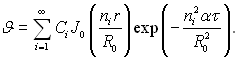(3.152)

Сталі величини С_і визначаються з початкових умов

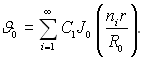(3.153)

Це співвідношення являє собою розклад функції J₀ в ряд за функцією Бесселя.

З курсу математики відомо, що система функцій є ортогональною. І як наслідок

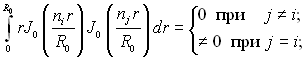(3.154)

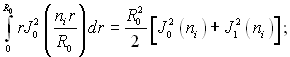(3.155)

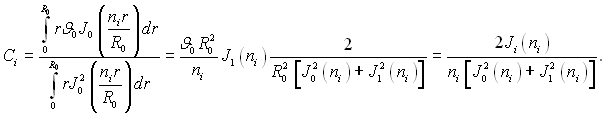(3.156)

Позначивши ? = J/J₀ = (t_p – t)/(t_p – t₀), отримаємо

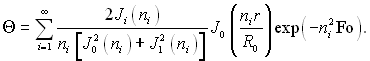(3.157)

У тому випадку якщо Fo ≥ 0,25, ряд (3.157) збігається досить швидко і для практичних розрахунків можна обмежитися першим членом ряду. При цьому безрозмірним перепадом температур на поверхні і на осі циліндра відповідають наступні залежності:

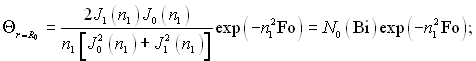(3.158)

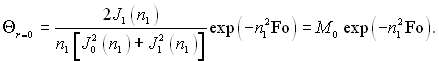(3.159)

Тому що в рівняннях (3.158) і (3.159) Θ є функцією тільки двох чисел подібності Bi і Fo, то для визначення Θ використовуються графіки подані на рис.3.15 і 3.16, подібні графікам для визначення Θ в пластині.

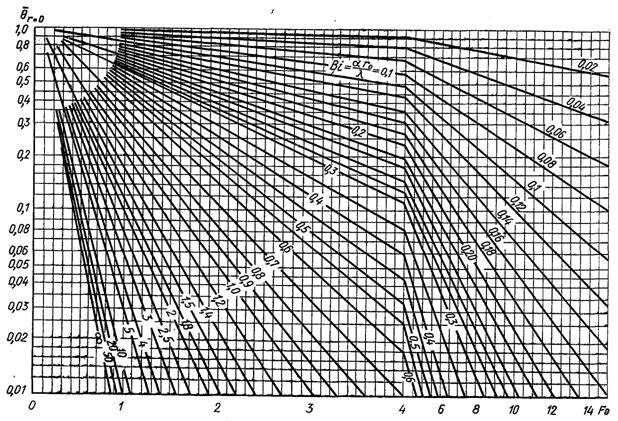
Рис.3.15. Залежність безрозмірного перепаду температур на осі необмеженого

циліндра від чисел Фур’є і Біо

Теплота, яка надходить в тіло за час  τ = 0...∞, повинна дорівнювати зміні ентальпії за цей же час:

(3.160)

Для проміжку часу, обмеженого τ₁, так само як і для пластини

Q₁ = Q(1 – Θ_cep), (3.161)

де 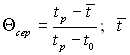– середня температура циліндра;

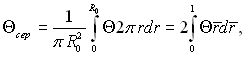(3.162)

де

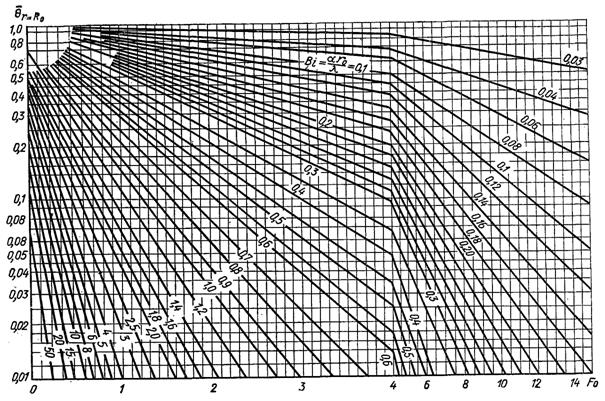
Рис.3.16. Залежність безрозмірного перепаду температур на поверхні

необмеженого циліндра від чисел Фур’є і Біо

Підставляючи значення Θ з (3.157) і інтегруючи вираз, отримаємо

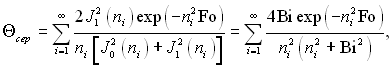(3.163)

тому що J₀(n_i)/J₁(n_i) = n_i /Bi, то у разі Fo ? 0,25

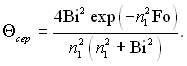(3.164)

Як уже відзначалося, визначення температурного поля циліндра кінцевої довжини здійснюється множенням рішень, отриманих для безмежного циліндра і необмеженої пластини.

3.8. Нестаціонарне температурне поле кулі

Розглянемо задачу з граничними умовами ІІІ роду: заданий коефіцієнт тепловіддачі α, постійний для всієї поверхні кулі, радіус якої R₀. У початковий момент часу τ = 0 температура кулі однакова у всіх точках і рівна t₀. Температура оточуючого середовища t_p > t₀. Надлишкова температура J = t_p – t.

Математично задача записується наступними рівняннями:

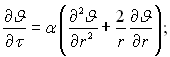(3.165)

(3.166)

З умови симетрії

(3.167)

(3.168)

Як і в попередніх випадках, при розгляді пластини і циліндра, задача може бути розв’язана методом розділу перемінних. Не виконуючи усіх розрахунків, обмежимося кінцевим результатом:

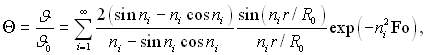(3.169)

де п_і – корінь характеристичного рівняння

tg n = –n/(Bi – 1). (3.170)

При

Ві → ∞  п_і = іπ і

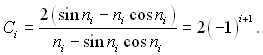
У наслідок цього рівняння (3.169) набуває наступного вигляду:

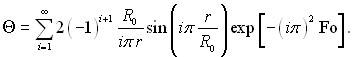(3.171)    

При малих значеннях Ві < 0,1 значення С_і прямують до нуля, за винятком С₁ = 1 і п₁² = 3Ві, тоді Θ набуває вигляду

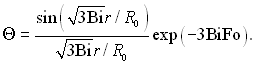(3.172)

При значеннях Fo ≥ 0,25  для виразу Θ у рівнянні (3.169) можна використати тільки перший член ряду

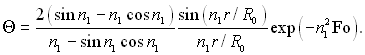(3.173)

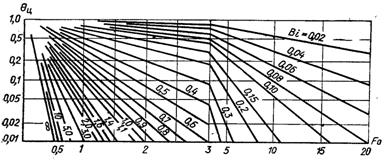
Рис.3.17. Залежність безрозмір-ного перепаду температур в центрі кулі від чисел Фур’є і Біо

Для визначення значення ? в центрі кулі (рис.3.17) чи на її поверхні (рис.3.18) можна використати графіки, де числа Ві являються параметром, а число Fo – аргументом.

За аналогією з пластиною і циліндром кількість теплоти, яка сприймається кулею за період часу від 0 до ?₁ визначається з рівняння:

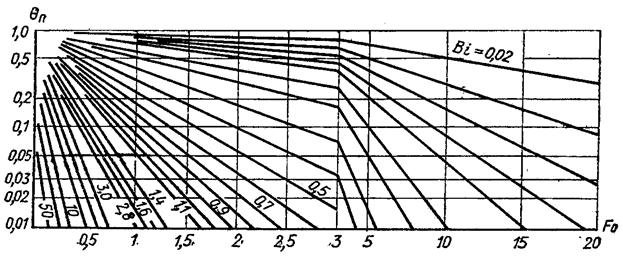
Рис.3.18. Залежність безроз-мірного перепаду температур на поверхні кулі від чисел Фур’є і Біо

 (3.174)

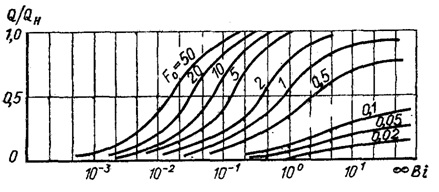
Рис.3.19. Графік для визначення кількості теплоти, яка сприймається кулею

Із (3.174) виходить, що Q/Q_н = = f(Bi, Fo). Визначити Q/Q_н можна за допомогою графіка рис.3.19, де

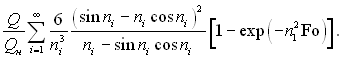(3.175)

повний приріст ентальпії кулі при нагріванні до t_p.