3.9. Регулярний режим процесів теплопровідності

Регулярним тепловим процесом називають нестаціонарний процес теплопровідності, під час якого поле надлишкової температури ( автомодельно в часі, тобто залишається подібним при зміні часу. Аналізуючи рішення, отримані для тіл різної форми (пластина, циліндр, куля), приходимо до висновку, що надлишкова температура може бути представлена рядом

(3.176)

де А_і – усталений коефіцієнт, який залежить від заданих початкових умов (числа Ві) і не залежить від просторових і часових координат; F_i – функція, що залежить від просторових координат і Ві. Специфіка геометричної форми враховується видом співмножників А_і і F_i.

Для першого члена ряду величину множника при τ  (входить у Fo) називають темпом регулярного режиму:

(3.177)

При малих значеннях τ  поле надлишкових температур визначається за формулою (3.176), тобто на розподіл надлишкових температур чинить вплив не тільки перший, але і наступні члени ряду. У цей період на формування поля надлишкових температур оказує суттєвий вплив початковий розподіл температур у тілі. Цей період називається неупорядкованим нестаціонарним процесом.

Тому що власні значення п_і зростають при збільшенні індексу і, то кожний послідовний член ряду (3.176) менше попереднього. Таке зменшення тим значніше, чим більше τ . Починаючи з певного значення часу (Fo > 0,3) поле надлишкових температур з достатньою точністю описується першим членом ряду (3.176); з цього моменту часу початкові умови відіграють другорядну роль:

( = А₁F₁exp(–mτ ) = J (x)exp(–mτ ). (3.178)

Цей період називається регулярним режимом.

З рівняння (3.178) при його логарифмуванні виходить, що

ln( = –mJ + const, (3.179)

тобто натуральний логарифм надлишкової температури змінюється в часі за лінійним законом. На рис.3.20 наведена ця залежність для двох точок тіла при його охолодженні.

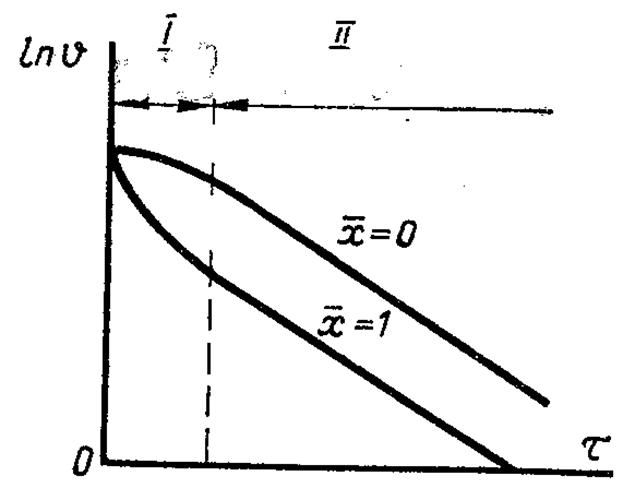
Рис.3.20. Залежність логарифма надлишкової температури від часу

Диференціюючи рівняння (3.179) за часом, отримаємо:

(3.180)

Темп охолодження, як видно з цього виразу, являє собою відносну швидкість зміни температури у тілі.

Темп охолодження можна визначити з графіка (рис.3.20), попередньо відшукавши для моментів часу J₁ і J₂ відповідні їм значення ln(₁ і ln(₂:

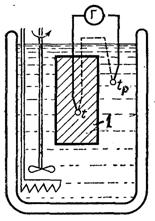
↑ Рис.3.21.Схема дослідної установки для вимірювання коефіцієнта температуропровідності методом регулярного режиму: 1 – дослідний зразок

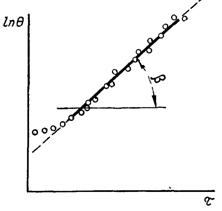
Рис.3.22. До визначення темпу регулярного режиму ↑

Вимірювання темпу регулярного режиму зазвичай виконують в наступному порядку. Дослідне тіло розміщують в термостат, в якому підтримується постійна температура рідини (рис.3.21). Рідина приводиться в рух гвинтом і інтенсивно обмиває поверхню тіла.

Двома термопарами, ввімкнутими “назустріч” одна іншій, вимірюється надлишкова температура J = t – t_p у довільній точці тіла в різні моменти часу. За результатами вимірів будується графік в напівлогарифмічних координатах lnJ, τ, як показано на рис.3.22. Величину темпу т визначають виміром катового коефіцієнта прямої лінії, яку утворюють дослідні точки після досягнення регулярного режиму. Слід зауважити, що цей метод визначення величини т годиться для речовин з низькою теплопровідністю [λ ≤ 0,5 Вт/(м·К)]. Дійсно, під час проведення досліджень необхідно забезпечити Ві ≥ 100, при цьому         λ ≤ αδ/100 Вт/(м·К). Величина коефіцієнта тепловіддачі α в термостатах не перевищує 2000 Вт/(м²·К), а розміри тіла не перевищують 2δ = 0,05 м. Отже,     λ ≤ αδ/Ві = 2000·0,05/(2·100) = 0,5 Вт/(м·К). Ця обставина обмежує використання регулярного режиму для вимірювання коефіцієнта температуропровідності в лабораторних умовах. Визначення коефіцієнта тепловіддачі на поверхні тіла, яке обмивається рідиною, також можна здійснювати за допомогою регулярного режиму нагрівання тіла.

Розглянемо тіло з об’ємом V і поверхнею F, яке охолоджується потоком рідини так, що число Біо мале (Ві ≤ 1). Розподіл температури в тілі з малим числом Ві недалекий від рівномірного, тобто температура в довільній точці тіла t (x, y, z) у даний момент часу τ незначно відрізняється від середньої в об’ємі температури t|(τ) у той же момент часу:

(3.181)

Розподіл температури у тілі визначається рівнянням Фур’є

(3.182)

і граничною умовою

(3.183)

Інтегруючи рівняння (3.182) за об’ємом, отримаємо:

(3.184)

Ліва частина цього виразу з урахуванням (3.181) перетворюється до:

(3.185)

Праву ж частину виразу (3.184) на підставі теореми Остроградського-Гаусса і умови (3.183) приводимо до виду

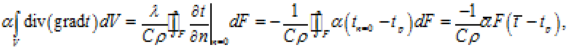(3.186)

де α|( – середній за площею коефіцієнт тепловіддачі.

Таким чином, з (3.185) і (3.186) виходить

(3.187)

чи

(3.188)

де

Загальний інтеграл рівняння (3.188) має вид:

Отже, і в розглядуваному випадку (для середніх температур і коефіцієнтів тепловіддачі) має місце експоненціальний регулярний режим. Величина т є темп зміни в часі середньої за об’ємом температури. Таким чином, для визначення середнього на поверхні тіла коефіцієнта тепловіддачі α| при малих значеннях чисел Біо (Ві ≤ 1) необхідно використовувати вираз

(3.189)

де т визначається способом, описаним вище.

Такий метод отримання середньої величини коефіцієнта тепловіддачі з поверхні тіла можна застосовувати тільки при невеликих температурних напорах, коли теплофізичні параметри рідини і тіла можна вважати постійними величинами.

Використання регулярного режиму для визначення в лабораторних умовах коефіцієнта тепловіддачі при зовнішньому обтіканні тіла обмежене невисоким значенням цього коефіцієнта. Дійсно, якщо взяти за вихідні параметри

 δ ≤ 0,25 м; λ ≤ 330 Вт/(м·К); Ві ≤ 0,1, то α| ≤ 0,1·330/0,025 ≈ 1300 Вт/(м²·К).

3.10. Хвильові теплові процеси

У техніці зустрічаються ряд пристроїв, в яких робочі процеси супроводжуються періодичним повторенням теплообміну, тобто має місце періодичної зміни температурного поля, названого температурними хвилями. Прикладом такого процесу може бути зміна температури в елементах конструкцій двигунів внутрішнього згорання, регенераторів, в елементах будівель, які піддаються періодичній дії сонячної радіації та інше.

У таких випадках закон зміни температурного поля не залежить від по-чаткового стану системи, а визначається певною періодичною функцією часу.

Розв’язок диференціального рівняння теплопровідності може здійснюватися методом розділу перемінних за умови, що функція, яка залежить від часу φ(τ), повинна бути періодичною. Таку умову задовольняє експоненціальна функція від уявного аргументу яка відповідає диференціальному рівнянню теплопровідності.

Як приклад розв’язку задачі з періодично змінним температурним полем розглянемо напівбезмежне тверде тіло, температура поверхні якого періодично змінюється в часі. Задача зводиться до вирішення рівняння:

(3.190)

при граничних умовах

t_с = f(?) при х = 0;

                                                        t_с = f(τ)  при  х = 0;                                    

                                                         t ≠ ∞  при  х → ∞.                                     (3.191)     

Якщо розв’язок шукати у вигляді добутку функцій

                                                  t = φ(τ) ψ(x),                                            (3.192)

то в наслідку отримуємо два диференціальних рівняння:

(3.193)

з рішення яких отримуємо

(3.194)

Цей вираз являє собою чотири окремих розв’язки, які [з урахуванням того, що ] мають вид:

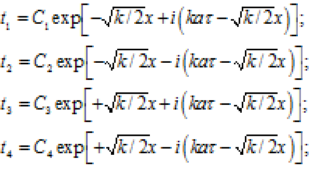(3.195)

з наведених окремих рішень два останніх не задовольняють фізичні умови задачі, тому що температура не повинна збільшуватися безмежно з ростом х. Отже, рішення t₃ і t₄ необхідно відкинути, а ті що залишилися t₁ і t₂ дають в сумі окремий розв’язок виду

(3.196)

чи, у разі переходу до тригонометричних функцій, матимемо:

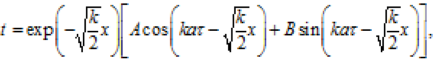(3.197)

де сталі А, В, k визначаються з граничних умов.

Тому що функція (3.191) t_c = f(?) є періодичною, то її можна виразити рядом Фур’є

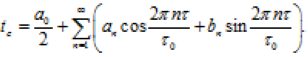(3.198)

При х = 0 рівняння (3.197) набуває наступного вигляду:

(3.199)

Порівнюючи між собою вирази (3.198) і (3.199) приходимо до висновку, що

                                                 А = а_п; В = b_n; k = 2πn/(aτ₀).                             

Постійний член а₀/2 у рівнянні (3.198), який являє собою середнє значення коливань температури при х = 0, не входить в рішення (3.197), тому що відображує початкову нерівномірність в момент часу τ = 0.

Таким чином, для досить великого значення τ рішення (3.197) набуває вид

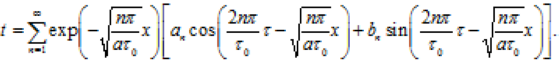(3.201)

Для більш простого випадку, якщо розглядаються коливання поверхні біля середньої температури

(3.202)

то рішення (3.201) зводиться до виразу

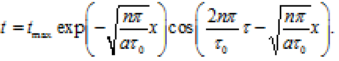(3.203)

де t_max – максимальна абсолютна зміна температури поверхні (максимальна амплітуда).

Максимальне значення температури має місце при cos2тπ = +1, тобто при т = 0, 1, 2, 3,..., чи

(3.204)

Момент часу, за якого температура досягає свого максимального значення

(3.205)

звідки виходить, що для любої відстані х, у тому числі і на поверхні, коливання температури мають один і той же період τ₀/п, але на відстані х від поверхні коливання запізнюються за фазою на і, крім цього, амплітуда коливань зменшується із-за наявності співмножника .

Довжину теплової хвилі визначаємо, прирівнюючи період коливань температури запізнення коливань за фазою:

(3.206)

Тепловий потік через поверхню тіла розраховується за формулою

(3.207)

попередньо визначивши значення градієнту температури на поверхні тіла:

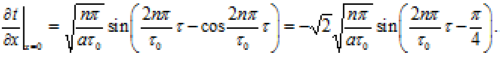(3.208)

Інтегрування градієнту температури за повний період дає нульове значення теплового потоку, а за півперіоду маємо:

(3.209)

3.11. Числові методи розв’язку задач теплопровідності

У найпростіших випадках розв’язок рівняння теплопровідності можна отримати аналітичним методом. Але для багатьох задач теплопровідності, які зустрічаються в сучасній техніці, цей метод неможливий. Наприклад, якщо необмежена плоска стінка з обох боків обмивається потоком нагрітого газу зі змінною в часі температурою і коефіцієнтом тепловіддачі, аналітичне вирішення цієї порівнянно простої задачі, зв’язаної з визначенням температурного поля в стінці, в загальному випадку наштовхується на труднощі. Крім цього, отримане рішення виходить на стільки громіздким, що без наступного програмування, рішення на ЕОМ і складання таблиць чи побудови номограм оказується непридатним для технічних потреб.

Крім змінних граничних умов, при інтенсивному теплообміні і великих перепадах температур, виникає необхідність урахування променевого теплообміну на межі тіла, зміна фізичних властивостей матеріалу з температурою, внутрішніх джерел теплоти і фазових переходів. При цих особливостях вирішення багатомірних нелінійних задач теплопровідності точними аналітичними методами, при сучасному стані математичного апарату, без пропозицій спрощення, не представляється можливим. У цьому випадку найбільш ефективними є наближені, числові методи.

Для вирішення диференціальних рівнянь типу теплопровідності найбільше поширення отримав метод кінцевих різностей чи метод сіток. Кінцево-різницевий метод розв’язку рівнянь в частинних похідних був запропонований ще в 30-і роки ХХ ст., але масове поширення отримав тільки після того, коли з’явилися швидкодіючі ЕОМ з достатньо великим об’ємом оперативної пам’яті.

При числовому вирішенні задачі різницевим методом неможна отримати рішення для всіх точок певної області простору. Наближений розв’язок можна отримати тільки для певної кінцевої множини точок, які називаються сіткою. Процес числового розв’язку починається з заміни диференціального рівняння його кінцево-різницевим аналогом.

Для того щоб написати різницевий аналог вихідного диференціального рівняння, необхідно, по-перше, замінити область безперервної зміни аргументу дискретною областю; по-друге, необхідно замінити диференціальний оператор рівняння так названим різницевим оператором. Після здійснення цього етапу задача про наближене числове вирішення зводиться до розв’язку системи лінійних алгебраїчних рівнянь (тобто системи кінцево-різницевих рівнянь). Близькість наближеного (різницевого) розв’язку до точного залежить від вибору сітки.

Розглянемо числові методи вирішення найбільш простих задач нестаціонарної теплопровідності. Для чисельного розв’язку таких задач можна використати різницеві рівняння, складені за явною чи неявною кінцево-різницевою схемою.

Явні кінцево-різницеві рівняння. При різницевому рішенні одномірного рівняння теплопровідності

(3.210)

похідні, які входять до нього, представляються (апроксимуються) похідними в кінцевих різницях:

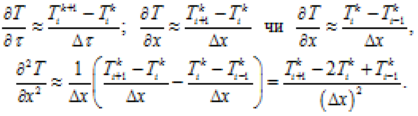
При цьому різницевий аналог диференціального рівняння теплопровідності приймає вид

(3.211)

У рівнянні (3.211) значення частинних похідних від температури Т в часі τ і від температури по координаті х замінені їх наближеними значеннями, а відповідні диференціали – кінцевими прирощеннями. У нашому випадку, Δх і Δτ – це малі прирощення незалежних перемінних х і τ  (Δх – крок по координаті, Δτ – крок по часу).

Під час розв’язку цього рівняння температури визначають тільки в окремих точках і = 1, 2, 3, ...п, які лежать на осі х. При цьому вважаємо, що у кожний момент часу τ розподіл температур у проміжку між сусідніми точками є лінійним. При розв’язку багатомірних задач ці точки зазвичай називають вузлами просторової сітки. Інтервали між ними в простому випадку однакові і рівні  Δх.

Вираз (3.211) необхідно розглядати як систему лінійних алгебраїчних рівнянь, число яких п дорівнює числу невідомих температур. індекси k і k +1 характеризують момент часу, якому відповідає значення температури: Т^k – значення температури в деякий момент часу τ; Т^k+1 – значення температури в момент часу τ +Δτ. Кожне із кінцево-різницевих рівнянь містять у собі тільки одну невідому температуру Т_і^k+1. Ця температура виникає у вузлі і після того, як пройде малий проміжок часу Δτ. При цьому вважається, що попередня температура у кожному з вузлів дорівнювала Т_і^k.

Наведена різницева апроксимація не являється єдино можливою. Рівняння (3.211)побудовано за явною класичною кінцево-різницевою схемою і легко розв’язується  в явному вигляді відносно невідомої функції.

Для розрахунку невідомих температур Т_і^k+1 система, яка складається з п алгебраїчних рівнянь типу (3.211), послідовно розв’язується для кожного кроку за часом. При цьому рівняння необхідно рішати стільки разів, скільки кроків (шарів) міститься в розрахунковому проміжку часу.

Коли виконується перший крок за часом і система (3.211) і система розв’язується перший раз, значення вихідних температур Т_і^k беруться з початкових умов. (Згідно початковим умовам, розподіл температур в момент часу τ = 0 повинен бути заданим). При наступних розв’язках значення  Т_і^k беруться з попереднього шару за часом.

Стійкість системи явних кінцево-різницевих рівнянь. Правильний вибір Δτ і Δх при рішенні системи кінцево-різницевих рівнянь має вирішальне значення. При використанні кінцево-різницевих схем величина допустимого кроку за часом обмежена і для внутрішніх вузлів залежить від вибраного кроку по координаті і температуропро-відності матеріалу а = λ/сρ.

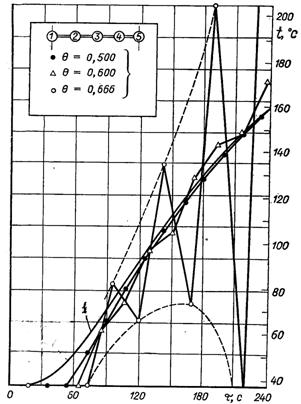
Рис.3.23. Стійкість системи явних кінцево-різницевих рівнянь[Θ = аΔτ/(Δх)²]: 1 – точне рішення

На рис.3.23 наведено результати точного і числового рішення задачі нестаціонарної теплопровідності для плоскої стінки, розбитої на чотири інтервали.

Порівняння показує, що розрахунки з аΔτ/(Δх)² = 1/2 приводять до задовільних результатів, у той самий час як при аΔτ/(Δх)² > 1/2 виникає явище нестійкості. Воно не пов’язане з помилками заокруглення, а є властивістю самої системи кінцево-різницевих рівнянь.

З наведеного прикладу виходить, що при виконанні розрахунків необхідно передусім потурбуватися щоб величина Δτ задовольняла умови стійкості системи кінцево-різницевих рівнянь.

Розв’язуючи рівняння (3.211) в явному вигляді відносно незмінної функції Т_і^k+1, отримуємо:

(3.212)

де А = С = аΔτ/(Δх)², В = 1 – 2аΔτ/(Δх)². При цьому А + В + С = 1.

Для простоти міркувань вважаємо, що всі Т > 0. У загальному випадку між відомих значень Т^k_i+1, Т_і^k і Т^k_i–1 знайдеться одне найбільше і одне найменше значення (У випадку двомірної задачі в правій частині рівняння (3.212) буде стояти п’ять різних температур, а у випадку тримірної – сім). Якщо вважати, що Т^k_i+1 має найбільше значення, а Т^k_i–1 – найменше, то у зв'язку з тим, що Т_і^k+1=Т^k_i+1–В(Т^k_i+1–Т_і^k)–С(Т^k_i+1–Т^k_i–1) і Т_і^k+1=Т^k_i–1+А(Т^k_i+1–Т^k_i–1)+В(Т_і^k–Т^k_i–1), при додатних А, В і С значення температури Т_і^k+1, яке необхідно вирахувати при рішенні, буде задовольняти нерівність Т^k_i+1 > Т_і^k+1 > Т^k_i–1 і, як наслідок, буде завідома обмежене. Величини А і С з фізичних міркувань не можуть бути меншими нуля, тому, для того щоб виключити необмежений ріст Т_і^k+1 під час розв’язку, при виборі ?? необхідно виконувати умову стійкості системи різницевих рівнянь, яка зводиться до наступного:

       В = 1 – 2аΔτ/(Δх)² ≥ 0 чи аΔτ/(Δх)² ≤ 1/2, тобто Δτ_доп = 0,5(Δх)²/а,

де Δτ_доп – максимально допустиме значення кроку в часі.

Використовуючи цей спосіб, можна вивести умову стійкості для випадку розв’язку багатомірних задач за розглянутою нами схемою, а також відшукати умови стійкості різницевих рівнянь, що відповідають вузлам, які знаходяться на границях тіла.

Наприклад, одномірне різницеве рівняння, наближено виражає умови теплового балансу для граничного вузла 1 різницевої сітки, може бути записане в наступному виді:

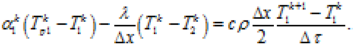(3.213)

У цьому рівнянні перший доданок лівої частини відображає тепловий потік, який переноситься шляхом конвекції від середовища з температурою Т_р1 до поверхні необмеженої плоскої стінки, другий – тепловий потік, який переноситься шляхом теплопровідності від граничного вузла 1 до вузла 2 твердого тіла, а права частина враховує зміну ентальпії тіла, яка відповідає товщині шару стінки Δх/2 за малий проміжок часу Δτ.

Усі члени цього рівняння віднесені до одиниці часу и одиниці площі поверхні стінки, крізь яку проходить тепловий потік.

Після приведення рівняння (3.213) до виду (3.212) визначають коефіцієнти при температурах Т₁^k і Т₂^k. Для дотримання умов стійкості вони повинні бути більшими нуля. Отже,

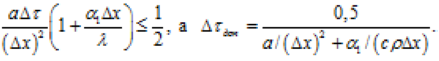
Отримані результати показують, що для граничного вузла сітки величина Δτ залежить не тільки від Δх і а, але також і від коефіцієнта тепловіддачі α₁. Ця умова стійкості для граничного вузла є більш жорсткою в порівнянні з умовою стійкості для внутрішніх вузлів. Ясно, що при проведенні розрахунків варто вибирати найменші значення Δτ_доп, які відповідають умові стійкості для граничного вузла 1.

В теорії кінцево-різницевих рівнянь показано, що при дотриманні умов стійкості рішення системи (3.211) наближається до точного розв’язку відповідного диференціального рівняння по мірі зменшення Δх і Δτ. Похибка апроксимації розглянутої різницевої схеми пропорційна Δτ і (Δх)². Але в окремому випадку, якщо Δх і  вибрані так, що аΔτ/(Δх)² = 1/6, похибка апроксимації суттєво зменшується і стає пропорційною (Δτ)² і (Δх)⁴. Цю обставину можна використати для підвищення точності чисельного розв’язку.

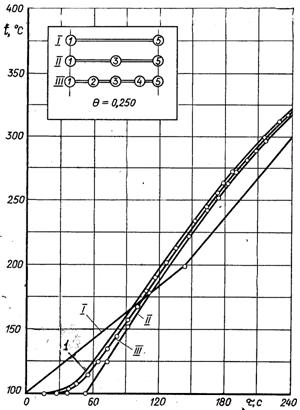
Рис.3.24. Збіжність числових рішень у залеж-ності від величини кроку по координаті Δх: 1 – точне рішення

Про вплив величини Δх на результати розв’язку можна судити по даним наведеним на рис.3.24. Криві І, ІІ і ІІІ відповідають рішенням, отриманим для двох, трьох і п’яти вузлів.

Неявні кінцево-різницеві рівняння.  З метою збільшення точності рішення Δх варто вибирати достатньо малим. Але в явних схемах найбільше допустиме значення Δτ пропорційне (Δх)². Це слідує з умов стійкості. За цих обставин може виявитися, що для закінчення процесу рішення необхідна велика кількість кроків у часі і розв’язок буде практично нездійсненним. В таких випадках для рішення рівняння теплопровідності використовуються неявні кінцево-різницеві рівняння виду

(3.214)

Явну і неявну кінцево-різницеві схеми можна об’єднати:

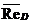(3.215)

тоді при σ = 0 отримуємо явну систему, а при σ = 1 – систему неявних кінцево-різницевих рівнянь.

Раціональний вибір вагового множника ? при машинних розрахунках дозволяє виконати рішення за тією схемою, яка в даних умовах вимагає мінімальних затрат машинного часу.

Покажемо, що при 0 ≤ σ < 1/2 система (3.215) стійка за умови, що аΔτ/(Δх)² ≤ (1–2σ). При 1/2 ≤  σ≤ 1 ніяких обмежень на стійкість не накладається і система рівнянь (3.214) є абсолютно стійкою. Точність рішення при використанні неявної схеми знову ж таки буде збільшуватися по мірі зменшення Δх, якщо Δτ також зменшується пропорційно (Δх)². Похибка апроксимації неявної схеми, так само як і для схеми (3.211) пропорційна Δτ і (Δх)².

Використовуючи абсолютно стійку неявну схему (3.214), можна суттєво збільшити крок за часом, вибираючи його в декілька разів більшим в порівнянні з  Δτ_доп для явної схеми. Але при цьому не слід забувати про те, що зі збільшенням  Δτ зростає похибка, яка з’являється внаслідок заміни диференціального рівняння його різницевим аналогом.

Застосування неявних схем в багатьох практичних випадках є дуже ефективною. Приймаючи в рівнянні (3.215)  σ = 1/2, отримаємо симетричну шести точкову різницеву схему підвищеної точності. Похибка апроксимації такої схеми пропорційна (Δτ)², (Δх)². При σ = 1/2 точність розрахунків збільшується, але за рахунок ускладнення схеми збільшується тривалість розрахункових операцій.

Розв’язок системи неявних кінцево-різницевих рівнянь. Система (3.214) абсолютно стійка, але процедура рішення неявних різницевих рівнянь ускладнюється тим, що кожне з них (за винятком рівнянь для границь) містить три невідомих температури Усі п рівнянь повинні розв’язуватися разом. При великій кількості рівнянь рішення такої системи класичними методами дуже громіздке і трудомістке. Але оскільки кожне рівняння містить не більше трьох невідомих функцій, то можна застосувати наступний метод, який найбільш ефективний для розглядуваних умов.

Представимо неявне різницеве рівняння (3.214) у такому виді

(3.216)

Лінійна залежність може бути виражена співвідношенням:

(3.217)

де Е_і і F_i – деякі поки невідомі коефіцієнти.

Аналогічні залежності (3.217), Підставимо отримане значення в (3.216) і виконуємо ряд елементарних перетворень, в наслідок цього отримаємо:

(3.218)

Порівняння виразів (3.217) і (3.218) показує, що в ролі Е_і і F_i у співвідношенні (3.218) знаходяться величини, які залежать від А_i, В_i, С_i, D_i, тоді

(3.219)

3.12. Дослідження теплопровідності методом аналогії

При різних умовах процес теплопровідності в твердих тілах може описуватися рівняннями теплопровідності Фур’є, рівнянням Лапласа і рівнянням Пуассона. Цими ж диференціальними рівняннями описуються також і деякі інші фізичні явища.

Різні за своїм фізичним змістом явища, математичний опис яких співпадає, прийнято називати аналогічними. Така аналогія існує, наприклад, між явищами теплопровідності і електропровідності, між явищами теплопровідності і дифузії. Поверхня, яка знаходиться під тиском тонкої мембрани описується тим же диференціальним рівнянням, що і температурне поле в певній області з рівномірно розподіленими джерелами теплоти. Відомо, що як функція току в усталеному потенціальному потоці нев’язкої рідини, так і функція теплового току в стаціонарному температурному полі за певних умов задовольняють одне і те ж рівняння Лапласа. Метод фізичної аналогії широко використовується для рішення задач як стаціонарної, так і нестаціонарної теплопровідності.

Це зв’язано з тим, що у багатьох випадках експериментальне дослідження аналогічних явищ оказується більш простим в порівнянні з безпосереднім дослідженням теплових явищ. За певних умов метод аналогій дозволяє отримати практично важливі результати в короткий час при незначних матеріальних затратах. Тут ми зупинимося тільки на методах електротеплової і гідротеплової аналогії.

Методи електротеплової аналогії. Для реалізації електротеплової аналогії існує безліч дослідних методів. Якщо для моделювання процесів теплопровідності використовують електричне коло, то таке моделювання називається електричним. Розрізняють два основних напрямки в реалізації електричних моделей: складання еквівалентних схем (схем заміщення чи аналогій) і створення аналогових обчислювальних машин (АОМ).

Порівнюючи рівняння, які стосуються математичного опису процесів теплопровідності і електропровідності (у двомірному наближенні), легко виявити аналогію між цими явищами.

Теплопровідність Електропровідність

(3.220)

(3.221)

(3.222)

(3.223)

У рівняннях (3.220)...(3.223) Т і u – температура і електричний потенціал; τ і τ₀ – час; dQ і dI  –  елементарні потоки теплоти і електричного струму, які проходять через площадки dF  і  dF_e у напрямку нормалі п і п_е; λ і σ – теплопро-відність і питома провідність; С і С_е – теплоємність і електрична ємність, віднесені до одиниці довжини; а – коефіцієнт температуропровідності; R_e – електричний опір, віднесений до одиниці довжини; ℓ_е – деякий лінійний розмір, який є аналогом відношення λ/α. Величини, які характеризують явище електропровідності відмічені індексом “е”. Рівняння (3.222) відображає граничні умови до диференціальних рівнянь (3.221). Рівняння (3.223) виражають зміну потоків Q і I в часі.

Аналогія здійснюється за умови а = λ/(сρ) = 1/(R_eC_e) і λ/α = ℓ_е, що може бути забезпечене вибором електричних величин і масштабів. При цьому аналогом температури Т є електричний потенціал и; аналогом теплового потоку Q – сила струму І, аналогом теплоємності С – електрична ємність С_е і аналогом термічного опору – електричний опір.

Моделюванню підлягають як стаціонарні, так і нестаціонарні процеси теплопровідності. При практичному використанні цієї аналогії тіло, теплопровідність якого підлягає дослідженню, розбивається на ряд елементарних об’ємів.

В еквівалентній електричній схемі ємності конденсатора в певному масштабі відтворюють теплоємність елементарного об’єму, пов’язаного з даною вузловою точкою тіла, в той час як електричні опори, також з дотриманням певного масштабу, відтворюють фактичні термічні опори між сусідніми вузлами. Ланка такого електричного кола, яка стосується однієї умовної точки і складена для випадку двомірної задачі нестаціонарної теплопровідності, наведена на рис.3.25. Відповідна ділянка кола для рішення тримірної задачі в кожній умовній точці містила б шість опорів і один конденсатор. При цьому необхідно мати на увазі, що аналоги у вигляді електричних кіл повинні також відтворювати граничні умови. Такі електричні кола можна назвати прямої аналогії. На відміну від них аналогові обчислювальні машини складаються з окремих блоків, які розв’язують елементарні математичні операції.

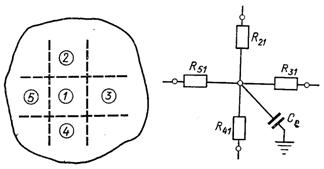
Рис.3.25. Двомірні моделюючі кола

Вирішення задач теплопровід-ності на аналогових обчислювальних машинах може бути практично зведене до розв’язку звичайних диференціальних рівнянь першого порядку, які мають наступний вигляд:

(3.224)

Систему (3.224) можна отримати з рівняння теплопровідності Фур’є, подавши другі похідні за температурою по координатам в кінцевих різницях (так як це було зроблене в попередньому параграфі).

У виразі (3.224) j – номер рівняння в системі; і – номер вузла різницевої сітки. Кількість рівнянь (k) співпадає із загальною кількістю вузлів; п ≥ 1; т ≥ k.

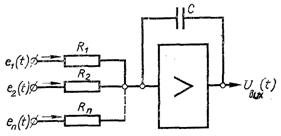
Рис.3.26. Схема інтегрального суматора операційного підсилювача постійного струму

При використанні АОМ кожне із звичайних диференціальних рівнянь системи розв’язується за допомогою операційних підсилювачів постійного струму (інтегруючого блоку), які сполучаються в одну загальну електричну схему. Умовна електрична схема інтегрального суматора наведена на рис.3.26. Кожний з таких блоків виконує математичну операцію, яка моделюється рівнянням

(3.225)

Це відповідає рішенню лінійного диференціального рівняння виду

(3.226)

У рівняннях (3.225) і (3.226) С – ємність конденсатора (рис.3.26); е(t) – напруга постійного струму, яка подається на вхід резисторів R_i (і = 1, 2, 3,..., п); t – машинний аналог часу.

Послідовно порівнюючи рівняння (3.226) з кожним з рівнянь системи (3.224), можна вирахувати передаточні коефіцієнти, які установлюють зв’язок між коефіцієнтами цих рівнянь. При цьому повинні враховуватися масштаби, які дозволяють перейти від перемінних системи (3.224) T_j, T_i і τ до відповідних машинних змінних е_і(t) і t.

Попередньо розраховані значення передаточних коефіцієнтів установлюються на АОМ шляхом підбору опорів R_i. Для визначення сталої и_вих0 використовуються початкові умови до задачі. Необхідна початкова напруга (и_вих0 ) створюється шляхом попередньої зарядки конденсатора з ємністю С.

Результати розв’язку у вигляді напруг на виході з кожного інтегруючого блоку [и_вих(t)] записуються осцилографом чи реєструються іншим приладом.

Гідротеплова аналогія. Для дослідження як стаціонарних, так і нестаціонарних процесів теплопровідності може використовуватися гідротеплова аналогія. У найпростішому випадку необхідну інформацію про цю аналогію можна отримати, порівнюючи відомі рівняння.

Теплопровідність Ламінарний рух рідини

З цих рівнянь слідує, що аналогом різниці температур (ΔТ) є гідравлічний напір (Δh); аналогом теплоємності (С) – гідравлічна ємність посудин, чи каналів, яка залежить від площі живого перерізу каналів (F_г); аналогом термічного опору (R) – гідравлічний опір (R_г).

Гідравлічна модель при цьому може будуватися у вигляді системи моделюючих гідравлічних ланок. Наприклад, у випадку розподілу температур в необмеженій плоскій стінці при нестаціонарному режимі стінка розбивається на кінцеву кількість шарів. В моделі кожний шар імітується вертикальною посудиною з перерізом пропорціональним теплоємності шару. Термічні опори шарів відповідають гідравлічним опорам капілярів, які з’єднують посудини. При ввімкненні витрат зміною рівнів рідини в посудинах в часі буде характеризуватися зміна температури в шарах стінки. Точність отриманих результатів буде залежати від кількості шарів. При побудові і роботі моделі необхідно враховувати початкові і граничні умови до задачі, а також масштаби для переходу від змінних, які характеризують явище, що вивчається, до змінних, які використовуються в моделі.

При моделюванні стаціонарних процесів картину ліній теплового току можна зробити візуально контрольованою.

У двомірному стаціонарному потенціальному (безвихровому) потоці нев’язкої рідини функцію току ψ(х, у) задовольняє рівняння Лапласа:

(3.227)

Лінії току ψ(х, у) =const в прозорій рідині гідравлічної моделі можна зробити видимими шляхом забарвлення потоку. Тому що функція теплового току в стаціонарних умовах (при відсутності внутрішніх тепловиділень) теж задовольняє рівняння (3.227), то видимі лінії току будуть аналогічні лініям теплового току і ортогональні до ізотерм.