




ЧАСТИНА ДРУГА КОНВЕКТИВНИЙ ТЕПЛООБМІН
![]()
Розділ 4. ОСНОВНІ ПОЛОЖЕННЯ КОНВЕКТИВНОГО ТЕПЛООБМІНУ
4.1. Основні положення і визначення
Конвективним теплообміном називається передача теплоти під час руху рідини. В реальних умовах конвекція теплоти завжди йде у супроводі з молекулярним переносом теплоти, а інколи і з променевим теплообміном.
Конвективний теплообмін між рухомим середовищем і поверхнею її розділу з другим середовищем (твердим тілом, рідиною чи газом) називається тепловіддачею.
Конвективний теплообмін під час руху рідини під дією неоднорідного поля масових сил (гравітаційного, магнітного, електричного) називається вільною конвекцією.
Конвективний теплообмін під час руху рідини під дією зовнішніх сил, прикладених на границях системи, чи однорідного поля масових сил, прикладених до рідини всередині системи, чи за рахунок кінетичної енергії, наданій рідині поза системою, називається вимушеною конвекцією.
Процес тепловіддачі називається стаціонарним, якщо поле температур в рідині не залежить від часу, і нестаціонарним, якщо розподіл температур в потоці залежить від часу.
В більшості практичних випадків, які розглядає теорія конвективного теплообміну, характерні розміри області течії рідких середовищ набагато більші довжини вільного пробігу молекул, що дозволяє розглядати рідкі середовища як безперервні. Виключення робиться тільки при аналізі процесу тепловіддачі розрідженого газу, коли розміри тіла стають спів розмірними з довжиною вільного пробігу молекул.
Отже, в подальшому розподілі температури в потоці рідини буде розглядатися у вигляді безперервного поля, для якого справедливі поняття градієнта температури grad t і вектора густини теплового потоку q.
Густина теплового потоку на поверхні теплообміну і коефіцієнт тепловіддачі. Основною задачею конвективного теплообміну є виявлення зв'язку між густиною теплового потоку на поверхні теплообміну, температурою цієї поверхні і температурою рідини. Безпосередньо біля поверхні теплообміну існує нерухомий шар рідини, крізь який теплота передається тільки шляхом теплопровідності. У цьому разі, згідно з гіпотезою Фур’є (1768...1830), маємо
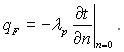 (4.1)
(4.1)
З цього рівняння виходить, що для визначення густини теплового потоку на стінці необхідно знати розподіл температур у потоці рідини.
Вже перші досліди по конвективному теплообміну показали, що у багатьох випадках густина теплового потоку пропорціональна різниці температур між рідиною і поверхнею тіла (закон тепловіддачі Ісаака Ньютона 1642...1727):
qF = α(tp – tст), (4.2)
де α – коефіцієнт тепловіддачі.
У загальному випадку пропорціональність між тепловим потоком і ризницею температур може порушуватися, але коефіцієнт тепловіддачі отримав широке розповсюдження у практиці теплотехнологічних процесів. Порядок величин коефіцієнта тепловіддачі для різних умов конвективного теплообміну, Вт/(м2·К):
Вільна гравітаційна конвекція в газах............5...30
Вільна конвекція води..................................100...1000
Вимушена конвекція газів..............................10...500
Кипіння води................................................2000...40000
Рідкі метали....................................................100...30000
Плівкова конденсація водяної пари.......... 4000...15000
Крапельна конденсація водяної пари.......40000...120000
Величина коефіцієнта тепловіддачі залежить від багатьох факторів. Найбільш суттєвими із них є: причина руху рідини (природна чи вимушена конвекція), режим течії (ламінарний чи турбулентний), швидкість руху рідини, теплофізичні параметри рідини (λр, μр, срр, ρр), геометрична форма тіла, наявність фазових переходів.
З рівнянь (4.1) і (4.2) виходить, що
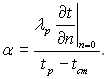 (4.3)
(4.3)
Зазвичай температура рідини в умовах теплопередачі змінюється від tp до tст в деякій області, названій тепловим пограничним шаром. У першому наближенні можна прийняти, що
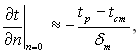 (4.4)
(4.4)
де δт – товщина теплового пограничного шару.
Тоді
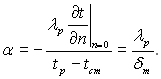 (4.5)
(4.5)
Рівняння (4.5) можна використати тільки для якісного аналізу. Так з цього рівняння слідує, що для збільшення коефіцієнта тепловіддачі необхідно використовувати рідини з високим значенням коефіцієнта теплопровідності і приймати міри, які ведуть до зменшення товщини теплового пограничного шару (збільшення швидкості руху рідини, густини, шорсткості поверхні, зовнішніх подразників, зменшення в’язкості рідини, розмірів поверхні). Кількісне визначення коефіцієнтів тепловіддачі є основною задачею теорії конвективного теплообміну.
Швидкий розвиток сучасної теплотехніки пов’язаний з безперервним ростом параметрів і збільшенні теплових потоків, які необхідно відводити з поверхні теплообміну, щоб запобігти її руйнуванню. Питомі густини теплових потоків різних джерел теплоти, з якими приходиться мати справу у сучасній техніці, Вт/м2:
Теплове випромінювання Сонця нормальне до поверхні Землі в полудень.....0,1
Теплообмінники на електричних станціях........................................................2·107
Реактивні двигуни на хімічному паливі.............................................................7·107
Тепловий потік головної частини космічних апаратів, що спускаються
на Землю (швидкість 11 км/с, маса 10 т)............................................................2·108
Реактивні двигуни на ядерному паливі..............................................................6·108
Термоядерні реактивні двигуни..........................................................................2·109
Лазерне випромінювання......................................................................................1012
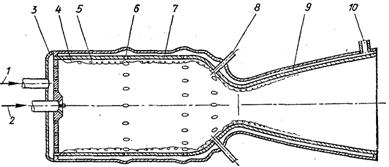
Рис.4.1. Внутрішнє охолодження камери рідинного ракетного двигуна: 1 – пальне; 2 – окислювач; 3 – головка камери згорання; 4 – рідинний захисний шар; 5 – паровий (газовий) захисний шар; 6 – подача пального для внутрішнього охолодження стінки; 7 – камера згорання; 8 – подача рідини для внутрішнього охолодження камери згорання; 9 – сопло; 10 – подача пального для зовнішнього охолодження стінки камери згорання двигуна
Суттєво ускладнюються і умови на поверхні теплообміну, про що можна судити з рис.4.1, де наведена схема охолодження ракетного двигуна.
Надійність роботи перспективних теплових двигунів в основному визначається надійністю системи охолодження проточної частини двигуна. У зв'язку з цим зростають підвищені вимоги до точності розрахунків теплообміну.
Сучасна теорія конвективного теплообміну ґрунтується на таких передумовах: 1) рухоме середовище, яке використовується для переносу теплоти, розглядається як суцільне середовище; 2) система диференціальних рівнянь, яка описує процеси конвективного теплообміну, виводиться на основі балансових рівнянь збереження енергії, речовини і кількості руху; 3) для замикання вихідної системи диференціальних рівнянь використовуються гіпотези, які установлюють зв’язок між тепловим потоком і градієнтом температури, а також між тертям і градієнтом швидкості; 4) фізичні параметри рідини (в’язкість μр, густина ρр, теплоємність ср і теплопровідність λр) ) вважаються відомими функціями параметрів стану.
4.2. Диференціальні рівняння теорії конвективного теплообміну
Закон збереження енергії для рухомого середовища. Перший початок термодинаміки для елементарного об’єму рухомого середовища можна записати так:
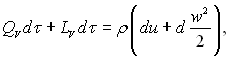 (4.6)
(4.6)
де QV – кількість теплоти в одиниці об’єму за одиницю часу, Вт/м3; LV – робота, яка здійснюється зовнішніми силами над одиницею об’єму середовища за одиницю часу, Вт/м3; τ – час, с; ρ – густина середовища, кг/м3; и – питома внутрішня енергія, Дж/кг; w – швидкість руху середовища, м/с.
З термодинаміки відомо, що
![]() (4.7)
(4.7)
де р – тиск, Па; υ – питомий об’єм, м3/кг.
З цього виходить, що
![]() (4.8)
(4.8)
Для визначення QV виділимо в розглядуваному середовищі кінцевий об’єм V, обмежений поверхнею F. Рівняння теплового балансу цього об’єму, віднесене до одиниці часу, можна записати так
![]() (4.9)
(4.9)
де qV – інтенсивність внутрішніх джерел теплоти (таких, як об’ємні хімічні реакції, радіоактивний розпад, робота тертя та ін.), Вт/м3.
Використовуючи формулу Гауса-Остроградського і припущення про суцільність середовища, маємо
![]() (4.10)
(4.10)
Тому що всі параметри є безперервними функціями координат і часу, з урахуванням (4.10) можна записати
![]() (4.11)
(4.11)
Приймаючи для вектора теплового потоку гіпотезу Фур’є, маємо
![]() (4.12)
(4.12)
З урахуванням рівнянь (4.6) і (4.12) отримуємо диференціальне рівняння енергії в наступній формі:
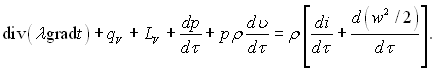 (4.13)
(4.13)
При помірних швидкостях руху рідини, коли робота зовнішніх сил і кінетична енергія потоку малі в порівнянні з його енергією, рівняння суттєво спрощується і приймає вид:
![]() (4.14)
(4.14)
де Di/dτ – субстанційна похідна, яка дорівнює
![]() (4.15)
(4.15)
Якщо коефіцієнт теплопровідності і питому теплоємність можна прийняти постійними, то
![]() (4.16)
(4.16)
чи з урахуванням (4.15):
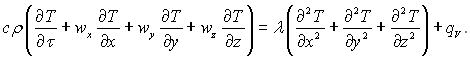 (4.17)
(4.17)
Для нерухомого середовища (w = 0) отримаємо відоме рівняння Фур’є-Кірхгофа (1.16)
![]() (4.18)
(4.18)
При відсутності внутрішніх джерел теплоти з рівняння (4.16) маємо
![]() (4.19)
(4.19)
де а – коефіцієнт температуропровідності.
У рівнянні енергії (4.12) невідомою величиною є швидкість руху рідини. Тому для визначення розподілу температури в потоці рідини необхідно попередньо розв’язати гідродинамічну задачу, тобто визначити розподіл швидкостей у потоці рідини.
Закон збереження маси у потоці рідини. Закон збереження маси рідини в довільному об’ємі V, обмеженому поверхнею F, можна записати так:
dMF = dM (4.20)
Введемо вектор густини потоку маси m, тоді
![]() (4.21)
(4.21)
В об’ємі V внаслідок зміни густини ρ накопичується маса
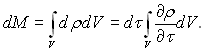 (4.22)
(4.22)
Підставивши значення dMF і dM з рівнянь (4.21) і (4.22) в рівняння (4.20), отримаємо:
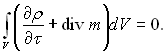 (4.23)
(4.23)
Об’єм V вибраний довільно, а всі параметри рідини у відповідності з прийнятими припущеннями про суцільність потоку є безперервними функціями координат і часу. На цій підставі з рівняння (4.23) слідує, що
![]() (4.24)
(4.24)
Вектор густини потоку маси зв’язаний з вектором швидкості і густини очевидним співвідношенням
т = ρw. (4.25)
Тоді
![]() (4.26)
(4.26)
чи в прямокутних координатах
![]() (4.27)
(4.27)
В окремому випадку, для плоскої течії
![]() (4.28)
(4.28)
для осесимитричної течії
![]() (4.29)
(4.29)
де r – відстань по нормалі до осі симетрії.
Рівняння (4.26) називається рівнянням нерозривності потоку.
Для нестисливої рідини ρ =const, тоді рівняння нерозривності буде
div w = 0, (4.30)
чи
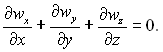 (4.31)
(4.31)
У рівняння нерозривності входять три компоненти швидкості wx, wy, wz і одного цього рівняння недостатньо для визначення поля швидкостей w у потоці рідини.
Закон збереження кількості руху в’язкої рідини. Диференціальні рівняння руху в’язкої рідини виводяться на підставі закону збереження кількості руху стосовно до рідини, яка тече через довільний об’єм V. Швидкість зміни головного вектора кількості руху рідини, яка знаходиться в об’ємі V, дорівнює головному вектору масових сил (ваги) і поверхневих сил, діючих на поверхню (сили тиску і сили тертя).
Головний вектор кількості руху рідини, що знаходиться в об’ємі V,
![]() (4.32)
(4.32)
Згідно до закону збереження кількості руху,
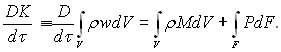 (4.33)
(4.33)
Ураховуючи, що
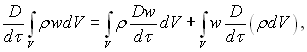 (4.34)
(4.34)
і перетворюючи поверхневий інтеграл в рівнянні (4.33) в звичайний по теоремі Гауса-Остроградського
![]() (4.35)
(4.35)
отримаємо
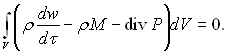 (4.36)
(4.36)
Використовуючи допущення про довільність об’єму V і суцільності середовища, маємо
![]() (4.37)
(4.37)
Ураховуючи, що
![]() (4.38)
(4.38)
отримуємо рівняння руху рідини, виражене в напруженнях Р:
![]() (4.39)
(4.39)
Це векторне рівняння і в проекціях записується у вигляді трьох рівнянь:
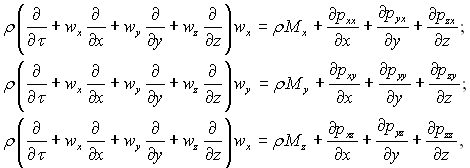 (3.40)
(3.40)
які містять 12 невідомих: три компоненти вектора швидкості (wx, wy, wz) і десять компонент тензора напруження (рxx, рxy, рxz, рyx, рyy, рyz, рzx, рzy, рzz ) і напруження зсуву. Нормальні напруження обумовлені силами тиску, а напруги зсуву викликані тертям між шарами рідини, яка рухається з різною швидкістю.
У відповідності з гіпотезою Ньютона дотичні напруження (напруга зсуву) в плоскому потоці в’язкої рідини зв’язані з похідною від швидкості по нормалі до напрямку потоку простим співвідношенням
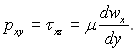 (4.41)
(4.41)
Коефіцієнт пропорціональності μ носить назву динамічної в’язкості і вимірюється в Па·с. Кінематичною в’язкістю ν називають відношення μ/ρ, і вимірюється в м2/с. Кінематична і динамічна в’язкості є фізичними параметрами рідини і залежать від температури і тиску рідини.
Динамічна в’язкість в основному залежить від температури. Для крапельних рідин динамічна в’язкість зменшується зі збільшенням температури, а для газів навпаки – підвищується.
Динамічна в’язкість газу в залежності від температури з достатньою точністю описується формулою Сазерленда
![]() (4.42)
(4.42)
і в окремому випадку, для повітря
![]() (4.43)
(4.43)
Для практичних розрахунків можна використовувати степеневу залежність:
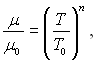 (4.44)
(4.44)
де п залежить від природи газу і його температури. В діапазоні температур від 300 до 2000 К можна приймати п = 0,75. Узагальнений закон Ньютона є лінійна залежність напруг від швидкості деформації рідини і може бути записаний так:
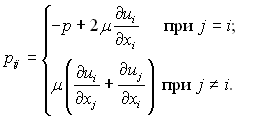 (4.45)
(4.45)
У цьому рівнянні р – тиск рідини в довільній точці потоку; координати х, у, z позначені через хі (і = 1, 2, 3) відповідно.
Рідини, які підпорядковані узагальненому закону Ньютона, називаються ньютонівськими рідинами.
Рівняння руху ньютонівських рідин у векторній формі має вид:
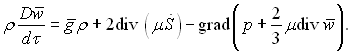 (4.46)
(4.46)
Тут ![]() – вектор з проекціями
Dwx/dτ,
Dwy/dτ,
Dwz/dτ;
– вектор з проекціями
Dwx/dτ,
Dwy/dτ,
Dwz/dτ; ![]() – тензор швидкості деформації, компонентами якого є:
– тензор швидкості деформації, компонентами якого є:
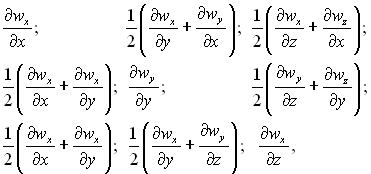 (4.47)
(4.47)
У проекціях на прямокутні координати векторне рівняння (4.46) записується у вигляді трьох рівнянь:
 (4.48)
(4.48)
Для ізотермічної течії нестисливої рідини (ρ = const, μ = const):
![]() (4.49)
(4.49)
у проекціях на прямокутні осі координат
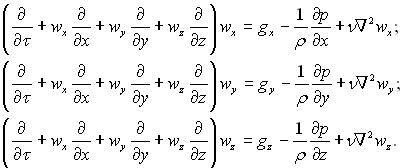 (4.50)
(4.50)
Проекція рівняння руху на ось х в циліндричних координатах має вид:
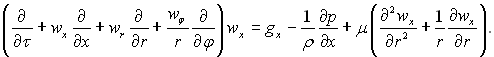 (4.51)
(4.51)
Система рівнянь (4.50) і (4.26) є замкнутою, тому що складається з чотирьох рівнянь і містить у собі чотири невідомих величини: ρ, wx, wy, wz.
У тому випадку, коли густина рідини змінна і залежить від температури, до рівнянь нерозривності і руху добавляється рівняння енергії і рівняння стану, які складають замкнену систему з шести рівнянь з шістьома невідомими.
Коли процес конвективного теплообміну супроводжується дифузією, густина рідини залежить як від температури, так і від концентрації компонент суміші. Для розв’язку подібних задач до вихідної системи рівнянь (4.13), (4.26) і (4.50) необхідно добавити рівняння дифузії компонент.
Диференціальне рівняння переносу маси. Розглянемо перенос маси даної речовини з густиною ρk у рухомому середовищі.
Допустимо, що у виділеному кінцевому об’ємі діють джерела чи стоки даної речовини інтенсивністю jVk [кількість речовини, яка виділяється (поглинається) за одиницю часу одиницею об’єму]. Тоді у всьому об’ємі V за одиницю часу буде утворюватися кількість речовини, рівне
![]() (4.52)
(4.52)
Частина речовини, яка проходить через поверхню S, обмежену вибраним об’ємом, з урахуванням формули Гауса-Остроградського становить:
![]() (4.53)
(4.53)
де j|kΣ – сумарний потік речовини викликаний молекулярною дифузією і концентрацією.
Рівняння балансу речовини для виділеного об’єму
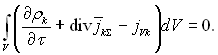 (4.54)
(4.54)
Тому що вибраний об’єм V довільний, а всі характеристики процесу є лінійні функції координат і часу, то можна написати
![]() (4.55)
(4.55)
Сумарний потік речовини можна подати у вигляді суми молекулярного і конвективного переносів:
![]() (4.56)
(4.56)
Молекулярний перенос маси відбувається під дією хімічного потенціалу "μ і градієнта температури "T. Для бінарних сумішів можна записати
![]() (4.57)
(4.57)
де К1 і К2 – постійні коефіцієнти.
У загальному випадку градієнт хімічного потенціалу k-го компонента буде
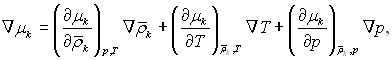 (4.58)
(4.58)
де ρ|k = ρk / ρ.
Позначивши коефіцієнт дифузії –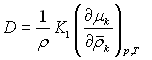 ; термодифузиційний коефіцієнт –
; термодифузиційний коефіцієнт –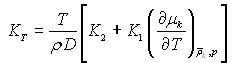 ; бародифузиційне співвідношення через
; бародифузиційне співвідношення через 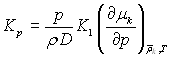 , будемо мати:
, будемо мати:
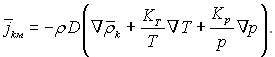 (4.59)
(4.59)
Перший член правої частини рівняння характеризує молекулярний перенос маси k-го компонента під дією градієнта концентрацій (закон дифузії Фіка), другий член визначає перенос маси за рахунок термодифузії (ефект Соре) і останній член характеризує бародифузію (дифузія маси під впливом градієнта загального тиску). У більшості випадків термодифузією і бародифузією можна нехтувати і обмежитися законом Фіка :
![]() (4.60)
(4.60)
Дифузійний перенос маси у багатокомпонентних сумішах досить складний. Якщо довільна газова суміш складається з двох груп компонентів, кожна з яких має приблизно однакову відносну атомну чи відносну молекулярну масу, то газ можна замінити ефективною бінарною сумішшю, для якої можна застосувати закон Фіка.
З урахуванням рівнянь (4.54), (4.56) і (4.60) отримаємо диференціальне рівняння дифузії k-го компонента:
![]() (4.61)
(4.61)
чи в декартових координатах
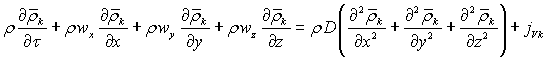 (4.62)
(4.62)
і в циліндричних координатах
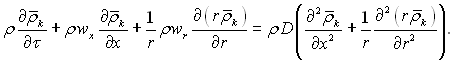 (4.63)
(4.63)
Рівняння дифузії типу (4.61) необхідно записати для кожного компонента суміші. Загальна кількість рівнянь дифузії на одиницю менша кількості компонент суміші, і тому для масових часток компонент маємо ще одну додаткову умову
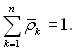 (4.64)
(4.64)
В окремому випадку, для суміші двох газів (бінарна суміш) достатньо до вихідної системи рівнянь добавити одне рівняння дифузії для якого-небудь компонента суміші.
Система рівнянь для турбулентного руху рідини. Із гідродинаміки відомо, що існує два режими руху рідини: ламінарний і турбулентний. При ламінарному режимі частинки рідини рухаються у потоці за певно визначеними головними траєкторіями, весь час зберігаючи рух у напрямку вектора середньої швидкості потоку, а виникаючі в потоці випадкові нерегулярності не розвиваються, а гаснуть. При турбулентному режимі руху виникають пульсації швидкості, окремі об’єми рідини рухаються поперек потоку, при цьому ці об’єми суттєво більші тих, до яких ще можна застосовувати поняття диференціального об’єму суцільного середовища. Отже, загальні рівняння гідродинаміки застосовувати і до турбулентного режиму руху.
Турбулентний рух, точно кажучи, є нестаціонарний, але якщо осередненні в часі швидкості не змінюються чи змінюються повільно, то дійсну швидкість можна представити у вигляді векторної суми
![]() (4.65)
(4.65)
де w( – вектор осередненої швидкості в даній точці; υ – вектор пульсаційної складової дійсної швидкості, який створює відхилення швидкості за величиною і напрямком від осередненого значення. Величина осередненої швидкості потоку в даній точці визначається інтегралом
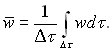 (4.66)
(4.66)
де проміжок часу Δτ повинен бути досить великим у порівнянні з періодом пульсацій, але в той же час повинен бути досить малим в порівнянні з яким-небудь характерним для осередненого руху інтервалом часу, щоб урахувати можливі зміни середніх швидкостей в часі.
У цьому разі
![]() (4.67)
(4.67)
оскільки за період Δτ всі пульсаційні складові швидкості взаємно компенсуються. Пульсації швидкості в турбулентному потоці викликають пульсації тиску, температури, концентрації та ін.
Для виводу рівняння осередненого турбулентного потоку, виконуючи вимоги Рейнольдса, приймаємо наступні правила осереднення:
1) якщо 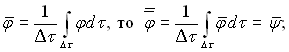 2)
2) ![]() 3)
3) ![]()
де Ф – пульсаційна складова φ.
Підставляючи в рівняння Нав’є- Стокса дійсні значення швидкості у відповідності з (4.65) і застосовуючи правила осереднення Рейнольдса для випадку руху нестисливої рідини, отримаємо:
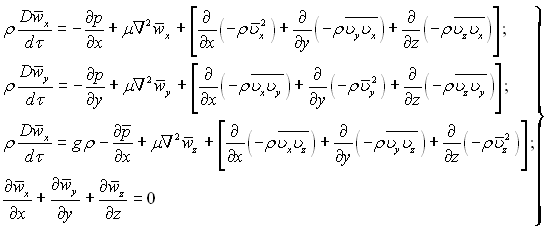 (4.68)
(4.68)
З наведених рівнянь видно, що пульсації швидкості викликають пульсації інших членів, які знаходяться у квадратних дужках, аналогічним за змістом членам в’язкісного тертя. Ці складові називаються турбулентними напруженнями і характеризують додатковий перенос кількості руху молярними об’ємами рідини, що рухаються внаслідок пульсацій швидкості.
В окремому випадку для плоского усталеного турбулентного потоку, коли швидкість w( – функція тільки поперечної координати у, з рівняння (4.68) маємо:
![]()
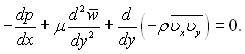 (4.69)
(4.69)
Введемо поняття турбулентної дотичної напруги:
![]() (4.70)
(4.70)
У цьому випадку для сумарних дотичних напруг
![]() (4.71)
(4.71)
Величина μт – називається турбулентною в’язкістю. На відміну від в’язкості μ турбулентна в’язкість не являється фізичним параметром. У розвиненому турбулентному потоці μт >> μ.
У неізотермічному турбулентному потоці пульсації швидкостей викликають пульсації температур і
![]() (4.72)
(4.72)
де Θ – пульсаційна складова температури Т.
Для випадку ρ = const і λ = const, застосовуючи до рівняння (4.19) правила осереднення, отримаємо
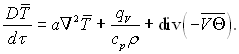 (4.73)
(4.73)
Вводячи поняття турбулентної теплопровідності 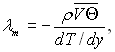 маємо
маємо
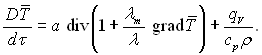 (4.74)
(4.74)
Аналогічним чином можна отримати і рівняння дифузії k-го компонента у турбулентному потоці:
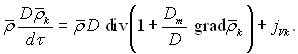 (4.75)
(4.75)
де Dm – коефіцієнт турбулентної дифузії.
Система диференціальних рівнянь турбулентного руху рідини є незамкнутою, тому що в рівняннях руху, енергії і дифузії з’явилися додаткові невідомі члени, які характеризують турбулентний перенос теплоти, маси і кількості руху. Для замикання цієї системи використовуються додаткові гіпотези, які складають основу напівемпіричних теорій турбулентності.
4.3. Умови однозначності конвективного теплообміну
Система диференціальних рівнянь (4.19), (4.26), (4.50) описує безмежну множину процесів конвективного теплообміну. Щоб виділити конкретний процес, необхідно сформулювати умови однозначності, які містять геометричні, фізичні, часові і граничні умови.
Геометричні умови визначають форму і розміри твердого тіла, на поверхні якого необхідно визначати q чи T, розташування поверхні нагріву в потоці рідини.
Фізичні умови визначають числові значення фізичних параметрів рідини μ, ρ, λ і ср, а також внутрішні джерела теплоти в потоці рідини.
Часові умови враховують особливості проходження процесу в часі і задаються у вигляді початкового розподілу температур і швидкостей.
Граничні умови визначають умови на поверхнях теплообміну і на границях потоку.
Горизонтальна складова швидкості на поверхні нагріву зазвичай приймається рівною нулю (умова прилипання рідини до стінки). Вертикальна складова швидкості на поверхні нагріву в загальному випадку може бути відмінною від нуля і задається певною величиною.
Теплові граничні умови включають в себе задані температури поверхні нагріву чи теплових потоків.
Так само як і в теорії теплопровідності, розрізняють три способи завдання теплових граничних умов.
Зазвичай ця умова записується так
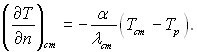 (4.76)
(4.76)
У деяких випадках температура поверхні нагріву чи тепловий потік у стінку не можуть задаватися і є шуканими параметрами. У цьому випадку до системи диференціальних рівнянь, які описують процес розповсюдження теплоти у потоці рідини, необхідно добавити диференціальні рівняння розповсюдження теплоти у стінці і задати умови спряження, які задаються у вигляді рівності температур на поверхні дотику середовищ чи у вигляді рівності теплових потоків через поверхні теплообміну.