Розділ 5. ОСНОВИ ТЕОРІЇ ПОДІБНОСТІ І РОЗМІРНОСТІ

5.1. Значення теорії подібності для теорії теплообміну

 

Вивчити явище – це значить виявити залежності між величинами, які характеризують це явище. Конвективний теплообмін – дуже складне явище, яке описується системою диференціальних рівнянь, які в загальному випадку складаються з рівнянь теплообміну, енергії, руху, нерозривності потоку, дифузії і стану. Диференціальні рівняння відображають тільки самі загальні риси явища, в них відсутні індивідуальні признаки конкретного одиничного випадку. Виділення конкретного випадку із загального класу явищ конвективного теплообміну здійснюється доповненням системи рівнянь умовами однозначності. Таким чином, система диференціальних рівнянь конвективного теплообміну і умови однозначності складають математичний опис конкретного випадку теплообміну.

В наслідок рішення системи диференціальних рівнянь конвективного теплообміну разом з умовами однозначності отримуємо залежності розподілу швидкостей, температур і концентрацій від координат і часу. Використовуючи формулу (4.3) знаходимо залежність коефіцієнта тепловіддачі α від часу τ, координат х, у, z, точки поверхні і значень усіх величин, які входять в умови однозначності ρ, μ, λ, ср та ін., тобто дійсно ця залежність і представляє найбільший практичний інтерес для інженерних розрахунків процесів теплообміну.

Зважаючи на непомірну складність диференціальних рівнянь конвективного теплообміну і умов однозначності, які містять велику кількість змінних, аналітичний розв’язок цієї задачі не можна отримати для загального випадку. Ці рівняння можна рішити в окремих випадках при суттєвих спрощеннях.

Якщо аналітично розв’язати задачу неможливо, то залежність для коефіцієнта тепловіддачі можна знайти чи числовими методами з великим обсягом розрахунків на ЕОМ, чи за допомогою експериментального дослідження. Відрізняючись способами отримання шуканих величин, обидва ці методи практично рівноцінні за можливостями при визначенні залежностей між величинами. Кожне окреме числове рішення, так само як і окремий експеримент, дають одне конкретне числове значення шуканої величини – коефіцієнта тепловіддачі при заданих значеннях вихідних аргументів. Щоб знайти залежність коефіцієнта тепловіддачі хоч для одного з аргументів, необхідно виконати множину експериментів чи виконати множину числових рішень при різних значеннях даного аргументу, залишаючи інші незмінними. Для знайденого ряду чисел можна далі підібрати необхідну експериментальну формулу, яка зв’язує коефіцієнт тепловіддачі з аргументами.

На відміну від формул, отриманих внаслідок аналітичного розв’язку диференціальних рівнянь, яки описують процес, емпіричні рівняння не відображають в повній мірі фізичної суті процесу. Вони справедливі тільки у тому діапазоні зміни аргументів, який був досліджений в експерименті чи отриманий числовими рішеннями. При цьому зміна значення хоч би одного з аргументів, які залишалися постійними в даній серії дослідів, може призвести до зміни характеру отриманої емпіричної залежності. При великій кількості аргументів дуже важко, а інколи і неможливо підібрати емпіричну залежність, яка правильно відображує вплив усіх аргументів. Таким чином, числові і експериментальні методи дозволяють отримати тільки роздрібненні залежності, узагальнення яких через мірно ускладнено великою кількістю аргументів, від яких залежить шукана величина. Такі труднощі дозволяє подолати теорія подібності.

Теорія подібності установлює умови подібності фізичних явищ і на цій підставі дає можливість суттєво скоротити кількість перемінних. Теорія подібності дає правила раціонального поєднання фізичних величин в безрозмірні комплекси, кількість яких суттєво менша кількості величин, з яких вони складаються. Ці комплекси відображають сумісний вплив сукупності фізичних величин на явище і можуть розглядатися як нові узагальнені змінні. Скорочення кількості змінних і використання їх в комплексному вигляді значно спрощує проведення експериментів і узагальнення результатів досліджень і числових рішень. Теорія подібності дає також правила моделювання процесів, які проходять в натурних умовах.

Поєднуються фізичні величини в безрозмірні комплекси теорією подібності на основі аналізу диференціальних рівнянь, які описують явище і містять загальні зв’язки між величинами. Але безрозмірні комплекси можна отримати і за допомогою теорії розмірності фізичних величин, суттєвих для явища.

 

5.2. Поняття про подібність фізичних явищ

 

Поняття подібності фізичних явищ в певній мірі можна вважати розширеним поняттям геометричної подібності. До геометрично подібних відносяться фігури однакової форми, відповідні кути яких рівні, а відповідні сторони пропорціональні (рис.5.1).

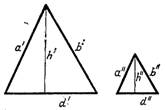
Рис.5.1. Геометрично подібні трикутники

Подібність цих трикутників (′ і ″)  можна виразити двома способами. Це може бути зроблено виявленням рівності відношень схожих відрізків подібних фігур. Таке відношення називається константою подібності:

а′ / а″ = b′ / b″ = d′ / d″ = h′ / h″ = c.

де а′, b′,  d′,  h′ – лінійні розміри одного трикутника;  а″, b″, d″, h″  – відповідні, схожі лінійні розміри другого подібного трикутника.

За допомогою константи подібності можна порівнювати між собою тільки дві подібні фігури, тому що для різних пар подібних фігур константи подібності – різні. Константа подібності показує, у скільки разів розміри однієї фігури відрізняються від розмірів другої, і від цього часто називається множником подібного перетворення.

Подібність трикутників можна виразити також рівністю відносних, безрозмірних схожих відрізків фігур. Безрозмірні відрізки виражаються відношенням довжини відрізка до довжини певного відрізка фігури, прийнятого як масштаб виміру всіх інших довжин. Якщо в подібних трикутниках за масштаб прийняти висоту h, то подібність трикутників виразиться рівняннями:

а′ / h′ = а″ / h″ = a| = idem;  b′ / h′ = b″ / h″ = b| = idem;  d′ / h′ = d″ / h″ = d| = idem.

Відносні безрозмірні елементи фігур можна називати інваріантами чи числами подібності. Використовуючи поняття відносної, безрозмірної довжини (число подібності), можна порівнювати довільну кількість подібних між собою фігур. При цьому всі подібні фігури, побудовані в одиницях масштабного розміру, тобто у відносних величинах, повністю однакові. Рівняння у відносних, безрозмірних величинах, які описують подібні фігури, оказуються теж однаковими. Це можна показати на наступному прикладі. Рівняння двох еліпсів можна записати так:

де а і b – відповідно велика і мала півосі еліпса. Приймаючи велику піввісь еліпса як масштаб виміру всіх інших довжин і віднесемо всі лінійні величини рівняння до цієї величини, можна записати рівняння еліпсів у відносних величинах:

де – відносні, безрозмірні перемінні; – відносні, безрозмірні величини малих піввісей еліпсів.

Для подібних еліпсів відносні, безрозмірні схожі довжини однакові. З цього слідує, що подібні еліпси мають тотожні рівняння у відносних величинах. При цьому число подібності, що знаходиться в рівняннях, чисельно рівне для них, тобто b(( = b(( = b( =idem. Іншими словами, подібні еліпси описуються одним і тим же рівнянням у відносних величинах:

Таким чином, якщо геометричні фігури можна представити рівняннями, то умовою їх подібності є однаковість, тотожність їх рівнянь у відносних, безрозмірних величинах. Багато корисних практичних задач можна розв’язати, якщо відомі умови подібності. Властивості подібних трикутників, наприклад, дозволяють визначити висоту дерева чи ширину річки без посереднього їх вимірювання.

Поняття подібності можна розповсюдити і на фізичні явища. Можна говорити, наприклад, про подібність руху потоків рідини – кінематичній подібності, про подібність сил – динамічна подібність, про подібність температур і теплових потоків – теплова подібність та ін.

Подібними можуть бути тільки явища однакової фізичної природи, які мають місце в геометрично подібних системах. Ознакою подібності є однаковість відносних, безрозмірних значень фізичних величин у всіх схожих точках. Схожими називаються точки, безрозмірні координати яких рівні, тобто точки, які задовольняють умову геометричної подібності. Тому що значення фізичних величин змінюються від точки до точки, то можна сказати, що ознакою подібності є однаковість, тотожність полів безрозмірних фізичних величин, побудованих у безрозмірних координатах. Відносне безрозмірне значення довільної фізичної величини отримують діленням дійсного значення цієї величини в даній точці на деяке характерне значення тієї ж величини, прийнятої як масштаб виміру цієї величини.

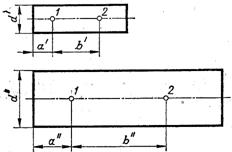
Рис.5.2. Подібність фізичних процесів під час руху рідини в трубах

Дамо пояснення подібних фізичних явищ на наступному прикладі. Допустимо, що є дві геометрично подібних системи наведених на рис.5.2, в яких мають місце подібні процеси течії рідини. Тоді, приймаючи як схожі точки 1 і 2, які задовольняють умову

можемо стверджувати, що має місце рівність при наявності

  •  кінематичної подібності

  •  динамічної подібності

  •  теплової подібності

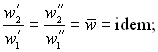
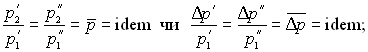
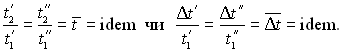
    Для подібності нестаціонарних явищ необхідна ще наявність часової подібності, яка визначає схожі моменти часу, в які в схожих точках повинні бути однаковими ті чи інші відносні величини подібності. Наявність часової подібності визначається наступним чином. Допустимо, що у початковий момент часу τ = 0 певна фізична величина φ1  у схожих точках двох систем мають значення φ′0 і φ″0. Через проміжок часу відповідно для систем при цьому φ′0 і φ″0. Через проміжок часу відповідно для систем при цьому Δτ′1 ≠ Δτ″1, у цих же схожих точках систем маємо значення фізичних величин φ′1 і φ″1. Через інший проміжок часу відповідно для систем Δτ′2 і Δτ″2 (Δτ′2 ≠ Δτ″2) значення фізичних величин в схожих точках систем φ′2 і φ″2. Якщо тепер при φ′2 / φ′1 = φ″2 / φ″1 = φ| = idem то це значить, що має місце часова подібність явищ – гомохронність. Якщо при цьому Δτ′2 = Δτ″2, то синхронність.

    Таким чином, при подібності фізичних явищ для любої фізичної величини, яка характеризує дане явище в схожих точках і в схожі моменти часу, повинно виконуватися співвідношення

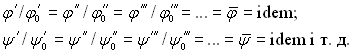    (5.1)

    Координати схожих точок і схожих моментів часу визначаються відповідно співвідношеннями:

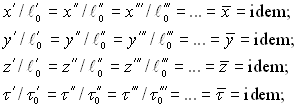    (5.2)

    Тому що у подібних фізичних явищах значення безрозмірних фізичних величин тотожні в схожих точках у схожі моменти часу, то функції, які виражають залежності безрозмірних фізичних величин від безрозмірних координат і часу

    також тотожні, однакові для всіх подібних між собою явищ.

    Подібні фізичні явища, як і геометрична подібність, можуть бути виражені за допомогою констант подібності. Із співвідношень (5.1) можна для двох подібних явищ записати

    Цей вираз можна переписати в наступній формі:

    Значення констант подібності Сφ і  Сψ показують, у скільки разів величини φ і ψ у системі відрізняються від аналогічних величин взятих у схожих точках подібної системи. Значення константи подібності даної фізичної величини однакове для всіх схожих точок двох систем з подібними фізичними явищами. Для фізичних величин різної фізичної природи значення констант подібності можуть бути різними. Поняття константи подібності використовується для попарного порівняння подібних явищ. Якщо існує декілька подібних явищ, то константи подібності при переході від одної пари явищ до іншої різні.

     

    5.3. Умови подібності фізичних явищ

     

    Розглядаючи геометричну подібність і подібність фізичних явищ, можна відмітити для них деякі загальні положення і на цій підставі сформулювати умови подібності фізичних явищ. У загальному випадку, за геометричної подібності і при подібності фізичних явищ, подібність виражається однаково і зводиться до тотожності відповідних безрозмірних величин. При геометричній подібності це відрізки фігур, при подібності фізичних явищ – різні фізичні величини.

    При геометричній подібності фігури, побудовані у відносних величинах, виходять однаковими, а рівняння, які описують ці фігури в безрозмірному вигляді – тотожні.

    При подібності фізичних явищ має місце тотожність полів відносних, безрозмірних фізичних величин, побудованих в безрозмірних координатах і в часі. Тотожними будуть і безрозмірні рівняння цих полів. Тотожність безрозмірних рівнянь полів фізичних величин у подібних явищ може бути тільки при тотожності математичних описів цих фізичних явищ в безрозмірному виді, тому що рівняння полів фізичних величин є, за своєю суттю, розв’язком диференціальних рівнянь, що описують явище разом з умовами однозначності.

    Отже, умова подібності фізичних явищ виражається в тотожності математичних описів подібних явищ в безрозмірному виді. Різниця криється тільки в змісті математичного опису.

    Математичний опис фізичного явища складається з системи диференціальних рівнянь і умов однозначності. Тому названа вище умова подібності можлива тільки тоді, коли, по-перше, розглядувані явища відносяться до одного і того ж класу явищ і описуються одною і тою ж системою диференціальних рівнянь, і тільки у цьому випадку рівняння явищ можуть бути тотожними в безрозмірному виді. По-друге, коли умови однозначності розглядуваних явищ якісно однакові, тобто містять у собі ті ж фізичні величини і одні і ті ж рівняння визначають розподіл цих величин у просторі і часі. Тільки у цьому випадку в усіх подібних явищах умови однозначності містять чисельно рівні відносні фізичні величини і тотожні безрозмірні рівняння, які описують поля відповідних величин в умовах однозначності. Ця умова включає в себе і геометричну подібність системи.

    Тепер необхідно виявити умови, яких необхідно дотримуватися, щоб рівняння, які описують явища одного і того ж класу, були тотожними. Для цього розглянемо процес приведення диференціальних рівнянь до безрозмірного виду.

    Диференціальні рівняння, які визначають конвективний теплообмін, у принципі прості – кожне з них представляє собою сукупність фізичних ефектів, що відображають закон збереження енергії чи маси. Наприклад диференціальне рівняння теплопровідності являє собою рівність кількості теплоти, підведеної до елемента середовища, і зміні ентальпії цього елемента dQ = di. Диференціальне рівняння руху відображає рівність усіх сил, діючих на елемент середовища, інерційній силі Fj = ΣFi. Отже, кожне диференціальне рівняння може бути записане в загальному виді, як алгебраїчна сума ефектів (сил, потоків теплоти та ін.)

    D1 + D2 + D3 +…+ Dn = 0. (5.3)

    Складання диференціальних рівнянь представляє собою перехід від складних фізичних понять – ефектів – до простих фізичних величин (густина, температура, в’язкість та ін.), тобто виражає собою фізичні ефекти через фізичні величини. Наприклад, складання диференціального рівняння теплопровідності заклечається в переході від рівняння в ефектах у вигляді dQ = di до рівняння між фізичними величинами у вигляді

    Таким чином, кожний ефект в рівнянні подається комбінацією фізичних явищ. Процес визначається сукупністю ефектів і від цього вплив окремих фізичних величин на процес проявляється в їх впливі на всю комбінацію величин, які характеризують ефект. З відси можна зробити висновок, що процес доцільно досліджувати у характерних для нього комбінаціях фізичних величин.

    Привести диференціальне рівняння (5.3) до безрозмірного вигляду можна таким способом. Розділивши і помноживши кожен член рівняння на масштаб ефекту, який він виражає, можна його представити у виді

    D = Пd,

    де D – член рівняння, який містить диференціальний оператор, що виражає певний фізичний ефект і такий що має розмірність ефекту; П – масштаб ефекту, представленого членом D. Масштаб ефекту являє собою комбінацію масштабних фізичних величин, які мають місце в ефекті. Ця комбінація величин має ефекту. Фізичні величини, які виконують роль масштабу, доцільно брати з умов однозначності, які задані при постановці задачі; d = D/П – член рівняння, який виражає відносний безрозмірний фізичний ефект. Це той же член D, тільки у відносних, безрозмірних величинах.

    Отже, рівняння (5.3) можна переписати в наступному виді:

    (5.4)

    Тому що всі члени рівняння вимірюються в одних і тих же одиницях, то всі масштаби ефектів П1, П2,... мають однакову розмірність. І якщо, розділимо усі члени рівняння на один із масштабів, наприклад на Пп, можна отримати рівняння в безрозмірному виді:

    (5.5)

    де π1п = П1/Пп, π2п = П2/П2п, ... – безрозмірні комплекси фізичних величин, які називаються визначальними числами подібності.

    Визначальні числа подібності складаються з величин, які знаходяться в умовах однозначності. Тому вони можуть бути розрахованими при постановці задачі, без її розв’язку чи експериментального дослідження. Числа подібності виражають відношення масштабів двох певних ефектів, суттєвих для явища. Кількість чисел подібності, які витікають з одного рівняння, на одиницю менше кількості членів рівняння.

    Безрозмірне рівняння (5.5) справедливе тільки для тих процесів, які стосуються одного класу, для яких усі числа подібності, що входять до цього безрозмірного рівняння, чисельно рівні. Отже, для того щоб рівняння, які описують явища одного класу, були тотожними у безрозмірному виді, необхідно, щоб однойменні числа подібності, які мають місце в цих рівняннях, були чисельно рівні. Тому рівність однойменних чисел подібності є умовою подібності явищ, які відносяться до одного класу і мають подібні умови однозначності.

    Таким чином, для того щоб фізичні явища були подібні, необхідно, щоб:

  •  явища були одного класу, тобто були одної фізичної природи і описувалися одною системою диференціальних рівнянь;
  •  умови однозначності явищ були якісно однаковими, тобто містили в собі одні і ті ж фізичні величини і одні і ті ж рівняння описували поля відповідних величин;
  •  однойменні визначальні числа подібності явищ були чисельно рівні між собою.

    В наслідок приведення до безрозмірного вигляду кожне диференціальне рівняння системи, яка описує процес, набуває вигляду рівняння (5.5)Ю в якому величини di містять диференціальні оператори над безрозмірними перемінними виду

    Очевидно, розв’язок системи рівнянь, що складається з рівнянь типу (5.5), повинен представляти собою деяку функцію, яка зв’язує значення всіх безрозмірних перемінних (залежної φ| і незалежних τ|, х,| у,| z|), чисел подібності, а також безрозмірних величин, які задаються умовами однозначності.

    Тому що масштабні фізичні величини для утворення відповідних безрозмірних величин беруться з умов однозначності, то всі безрозмірні величини умов однозначності, які прийнято за масштабні, дорівнюють одиниці. У рішення ввійдуть тільки безрозмірні відношення величин одної і тієї ж фізичної природи з умов однозначності (розміри, температура та ін.), наприклад Рℓ =ℓ1/ℓ0, Рt = Т1/Т0. Такі відношення називаються параметричними числами.

    Отже, розв’язок системи безрозмірних диференціальних рівнянь набуває наступного вигляду:

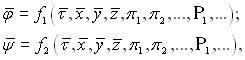    (5.6)

    де φ|, ψ| ... – залежні (шукані) безрозмірні параметри; τ|, x,| y,| z| – незалежні безрозмірні параметри (час і координати); π1, π2 ,... – визначальні числа подібності, які задані умовами однозначності і для конкретної задачі є сталими величинами; Р1, Р2 – параметричні числа подібності, які задаються умовами однозначності і постійні для конкретної задачі.

    Рівняння типу (5.6) називаються безрозмірними рівняннями подібності. Кожне рівняння подібності описує всі подібні між собою явища. Якщо немає необхідності визначати шукану величину, наприклад коефіцієнт тепловіддачі, в кожній точці поверхні і в кожний момент часу, а достатньо середнього його значення за всією поверхнею і за весь проміжок часу, то в рівнянні відсутні значення безрозмірних координат x,( y,( z( і часу τ( і рівняння набуває вигляду:

    (5.7)

    В окремих випадках, коли ті чи інші ефекти не проявляються в процесі, деякі числа подібності, що містять масштаби цих ефектів, можуть бути відсутніми в рівняннях подібності. У такому випадку спостерігається автомодельність явища по відношенню до даного числа подібності. У рівняннях подібності, які описують процеси з однаковими умовами однозначності, відсутні параметричні числа подібності. Отже, наявність в рівнянні параметричного числа подібності, наприклад відношення розмірів, свідчить про те, що це рівняння подібності враховує певну неподібність систем.

    До всього, що сказано про числа подібності, необхідно добавити, що вигляд чисел подібності, які отримані з диференціального рівняння, залежить від того, на масштаб якого ефекту ділимо члени рівняння, коли приводимо його до безрозмірного вигляду. Але системи чисел подібності, отримані з однієї і тої ж системи рівнянь і умов однозначності, еквівалентні одна іншій. Довільна комбінація з чисел подібності є теж числом подібності і може замінити в рівнянні подібності одне з чисел подібності, яке входить у цю комбінацію. Цим правилом користуються для виключення з числа подібності величини, яка не міститься в умовах однозначності. Це здійснюється шляхом сполучення двох чисел подібності, які містять у собі цю величину. При цьому кількість чисел подібності зменшується, тому що отримане число подібності заміняє тільки одне число подібності. Сполученням безрозмірної перемінної (аргументу чи функції) з числом подібності можна замінити в безрозмірній перемінній на задану в умовах однозначності масштабну величину комплексом інших масштабних величин. Отримана при цьому безрозмірна змінна має вигляд числа подібності з тією різницею, що містить у своєму складі перемінну величину, у той час як числа подібності складаються виключно із постійних величин, відомих з умови задачі. Такі перемінні, які мають вид чисел подібності, неможна використовувати як ознаки подібності, тому що їх неможна розрахувати до розв’язку задачі. З цієї причини їх називають не визначальними числами подібності. Крім цього, кожне відносне значення шуканої величини при певному значенні визначальних чисел подібності, справедливе для багатьох подібних між собою випадків, тому що одне і те ж значення чисел подібності можна отримати за допомогою різних цифрових значень величин, які входять у нього.

    Таким чином, отримана на засадах теорії подібності форма представлення рішення системи диференціальних рівнянь в безрозмірному виді дозволяє: по-перше, скоротити число аргументів, чим спрощує опрацювання дослідних даних, і дає можливість отримати залежність між величинами; по-друге, узагальнити дані одиничного досліду чи числового рішення на множину подібних між собою випадків.

    Основні положення теорії подібності зводяться до трьох теорем. Перша теорема стверджує, що у подібних явищах усі числа подібності (визначальні і не визначальні) повинні бути чисельно рівні. Друга стверджує, що рішення диференціального рівняння можна представити у вигляді зв'язку між числами подібності, які отримані з цього рівняння. Третя теорема говорить, що явища подібні, якщо вони мають подібні умови однозначності і чисельно дорівнюють числам подібності, що містять величини з умов однозначності (визначальні числа подібності). Ці теореми відображають умови подібності і особливості подібних явищ, які були розглянуті нами.

    З розглянутого виходить, що теорія подібності не дає розв’язку, а тільки дозволяє узагальнювати експериментальні дані, вказуючи форму, у якій ці дані повинні представлятися. Отже, теорія подібності є теорією експерименту, і тому її значення особливо велике для наукових областей, основою яких є експеримент чи цифрове рішення. Дійсно до такої області відноситься і конвективний теплообмін.

    •