




5.4. Числа і рівняння подібності конвективного теплообміну
Для виявлення виду чисел подібності необхідно систему рівнянь конвективного теплообміну привести до безрозмірного виду. Система диференціальних рівнянь конвективного теплообміну для руху нестислої рідини з постійними фізичними параметрами являє собою сукупність:
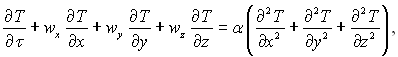 (5.8)
(5.8)
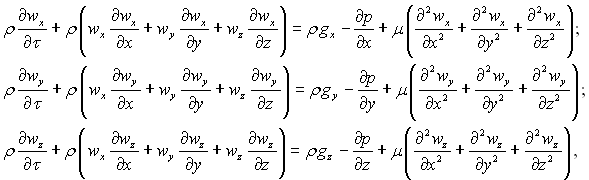 (5.9)
(5.9)
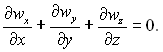 (5.10)
(5.10)
До систем диференціальних рівнянь (5.8)...(5.10) добавляються умови однозначності. У нашому випадку цю умову можна записати в виді
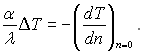 (5.11)
(5.11)
Іноді це рівняння називають рівнянням теплообміну, тому що воно включає в себе шукану величину – коефіцієнт тепловіддачі.
У цих рівняннях можна виділити два види параметрів: незалежні змінні τ, х, у, z; залежні змінні (невідомі величини) α, Т, wx, wy, wz, p. Залежні змінні однозначно визначаються значеннями незалежних змінних, якщо задані постійні величини, що входять в умови однозначності, w0,T0,ℓ0, μ, a, λ, ρ та ін.
Для приведення рівняння до безрозмірного виду необхідно вибрати масштаби для залежних і незалежних величин. За масштабні величини найбільш доцільно приймати величини, які входять в умови однозначності і задаються при постановці задачі. Далі необхідно замінити абсолютні значення всіх змінних відносними, безрозмірними величинами, використовуючи визначення безрозмірної величини, а саме:
φ| = φ / φ0,
де φ0
– масштабне значення фізичної величини φ. Звідси абсолютна величина φ
може бути виражена через безрозмірну φ|
і масштабну φ0 у виді
φ = φ0φ|(. (5.12)
Тому що вихідні рівняння містять перші і другі похідні змінних величин, то необхідно і для них отримати відповідні вирази. Це можна зробити з використанням виразу (5.12) наступним чином:
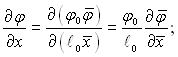 (5.13)
(5.13)
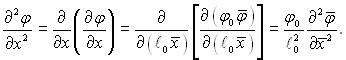 (5.14)
(5.14)
Кожний член з диференціальним оператором в рівняннях відображає певний фізичний ефект і є математичним виразом для кількісного визначення цього ефекту, тобто є правилом визначення ефекту в самому загальному випадку, коли він змінний. Звідси комбінація з постійних масштабних величин, яка знаходиться перед диференціальним оператором у відносних величинах, представляє собою масштаб ефекту. Ця комбінація виражає закон формування фізичних величин в ефекті. Правило визначення ефекту і закон формування величин в ньому співпадають, тобто однакові математичні вирази у разі постійності ефекту. Наприклад, правило визначення прискорення має вид
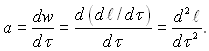
Якщо прискорення постійне а = const, то правило його визначення можна представити у виді а = w/τ = ℓ/τ2. Цей вираз представляє собою комбінацію фізичних величин в прискоренні, тобто виражає закон формування фізичних величин в ньому.
Прийнявши масштаби для коефіцієнта тепловіддачі α0, довжини ℓ0, швидкості w0, часу τ0, температури Т0 і тиску р0 і використовуючи вирази (5.12), (5.13) і (5.14) представимо рівняння теплообміну в наступному виді:
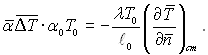 (5.15)
(5.15)
Розділивши отримане рівняння (5.15) на комплекс масштабних фізичних величин, які виражають масштаб другого ефекту П2 = λТ0/ℓ0, запишемо рівняння в безрозмірному виді:
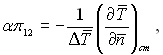 (5.16)
(5.16)
де π12 – безрозмірний комплекс із масштабних величин, які представляють собою відношення масштабних ефектів П1 = α0Т0 і П2 = λТ0/ℓ0:
π12 = П1/П2 = α0ℓ0/λ. (5.17)
Зазвичай в умовах однозначності не знаходиться величина коефіцієнта тепловіддачі α0, тому необхідно перетворити відносну величину α| і π12. Масштабне значення коефіцієнта тепловіддачі α0 у величині α| необхідно замінити комплексом величин з умов однозначності. З виразу для числа подібності π12 видно, що таким комплексом є відношення λ/ℓ0. Отже добуток α| π12 = (α/α0)(α0ℓ0/λ) = αℓ0/λ в рівнянні (5.16) представляє собою відносну величину невідомого коефіцієнта тепловіддачі. Цей комплекс є не визначальним числом подібності і носить назву числа Нуссельта:
![]() (5.18)
(5.18)
Число Нуссельта характеризує співвідношення між конвективним переносом теплоти від рідини до поверхні тіла (qст) і переносу теплоти теплопровідністю крізь шар рідини товщиною ℓ0 (qстλ). Дійсно, з рівняння (5.18) виходить, що
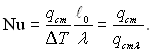 (5.19)
(5.19)
У задачах конвективного теплообміну число Нуссельта є шуканою величиною. За своєю структурою число Нуссельта подібне за структурою до числа Біо (Ві = αℓ0/λм), але на відміну від нього містить коефіцієнт теплопровідності рідини і має інший фізичний зміст.
Таким чином, безрозмірне рівняння теплообміну в кінцевому виді можна записати так:
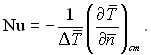 (5.20)
(5.20)
З урахуванням виразів (5.12)...(5.14) рівняння енергії перетворюється до наступного виду
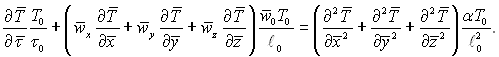 (5.21)
(5.21)
Розділивши члени рівняння на комплекс величин, які виражають масштаб ефекту і є третім членом рівняння П3 = αТ0/ℓ02, запишемо його в безрозмірному виді:
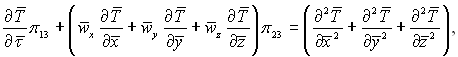 (5.22)
(5.22)
де π13 = П1/П3 = ℓ02/(ατ0) і π23 = П2/П3 = w0ℓ0/α – числа подібності.
Числа подібності прийнято позначати першими двома літерами прізвищ вчених, які зробили суттєвий внесок у розвитку даної області знань, і відповідним чином іменувати.
На практиці числа подібності, які ґрунтуються і виходять з цього рівняння, зазвичай використовуються у вигляді чисел Фур’є і Пекле. Число Фур’є
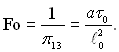 (5.23)
(5.23)
Число Фур’є виражає співвідношення між теплом зміни умов в оточуючому середовищі і теплом перебудови температурного поля всередині тіла.
Число Пекле
![]() (5.24)
(5.24)
Число Пекле виражає співвідношення між інтенсивністю переносу теплоти конвекцією і інтенсивністю переносу теплоти теплопровідністю.
Рівняння руху для осі х з урахуванням виразів (5.12)...(5.14)
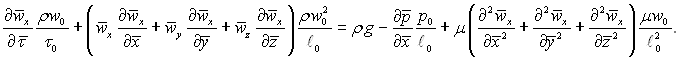 Розділивши це рівняння на комплекс величин біля другого члена рівняння, який
виражає масштаб інерційних сил
П2 = ρw02/ℓ0, отримаємо рівняння в безрозмірному виді:
Розділивши це рівняння на комплекс величин біля другого члена рівняння, який
виражає масштаб інерційних сил
П2 = ρw02/ℓ0, отримаємо рівняння в безрозмірному виді:
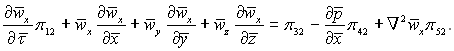 (5.25)
(5.25)
У цьому рівнянні π12 = П1/П2 = ℓ0/(τ0w0), π32 = П3/П2 = gℓ0/w02, π42 = П4/П2 = = p0/(ρw02), π52 = П5/П2 = ν/(w0ℓ0) – числа подібності.
На практиці використовуються наступні числа подібності, які отримані з рівняння руху.
Но = 1/ π12 = τ0w0/ℓ0. (5.26)
Число гомохронності виражає міру відношення переносного (конвективного) прискорення до прискорення в даній точці.
Fr = π32 = gℓ0/w02. (5.27)
Число Фруда виражає співвідношення між силою тяжіння і інерційною силою в розглядуваному явищі, що слідує з рівняння (5.27), якщо його записати у виді Fr = ρgℓ0/(ρw02). Воно має суттєве значення у тих випадках, коли гравітаційні ефекти відіграють помітну роль. В окремих випадках ефекти, обумовлені дією сили тяжіння, настільки незначні, що ними можна нехтувати. Зазвичай в умовах однозначності не містяться величини тиску р0. Виходячи з цього масштаб тиску у відносному тиску р| слід замінити комплексом величин з умов однозначності. Виходячи з виразу для числа подібності π42 = p0/(ρw02), в якому комбінація величин ρw02 має розмірність тиску і нею можна замінити масштаб у безрозмірному тиску. З цього виходить, що добуток
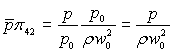 (5.28)
(5.28)
представляє собою невідомий за умови відносний тиск. Цей комплекс є не визначальним числом подібності.
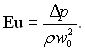 (5.29)
(5.29)
Число Ейлера виражає співвідношення між силою тиску і інерційною силою в розглядуваному явищі.
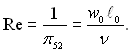 (5.30)
(5.30)
Число Рейнольдса виражає співвідношення між силою інерції і силою внутрішнього тертя, у цьому можна переконатися, якщо записати число Рейнольдса в наступному виді
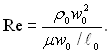 (5.31)
(5.31)
Чим менше число Рейнольдса, тим більший вплив на всі гідродинамічні характеристики потоку оказують молекулярні сили в’язкості і тим стійкіше в’язка, ламінарна течія рідини. При певному (критичному) значенні числа Рейнольдса ламінарний режим руху переходить у турбулентний. Як буде показано нижче, інтенсивність конвективного теплообміну суттєво залежить від режиму течії рідини, тому число Рейнольдса є одним з основних визначальних чисел подібності теорії теплообміну і гідродинаміки.
Рівняння руху для осей у і z приводяться до безрозмірного виду аналогічним чином і, як легко собі представити, дають ті ж самі системи чисел подібності.
Застосувавши вирази (5.12)...(5.14), рівняння нерозривності потоку запишеться так:
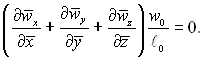
Тому що w0/ℓ0 не дорівнює нулю, то
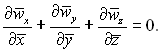 (5.32)
(5.32)
З цього виразу видно, що безрозмірне рівняння нерозривності потоку для нестислої рідини (ρ = const) не містить у собі чисел подібності.
Використовуючи позначення чисел подібності, можна записати систему безрозмірних рівнянь конвективного теплообміну:
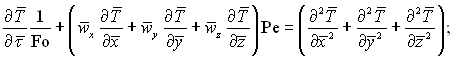 (5.33)
(5.33)
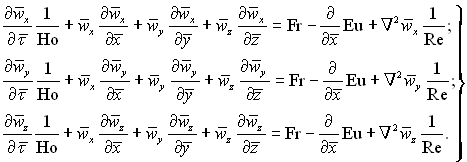 (5.34)
(5.34)
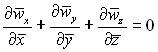 (5.35)
(5.35)
і рівняння теплообміну
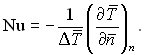 (5.36)
(5.36)
Розглянемо ще декілька чисел подібності, які застосовуються при розв’язку задач конвективного теплообміну. Під час аналізу вільного руху рідини неможливо завідома вибрати яку-небудь швидкість в якості масштабу, тому що вона відсутня в умовах однозначності. Таким чином число Рейнольдса і Фруда не можуть бути визначальними в цих умовах. Але комбінуючи ці два числа подібності, можна отримати нове число подібності, яке не буде містити в собі швидкості.
![]() (5.37)
(5.37)
Число Галілея характеризує відношення масових сил до сил в’язкості.
Якщо розглядати випадок вільного руху, обумовленого неоднорідністю поля густин, то до системи чисел подібності необхідно добавити число подібності параметричного типу Δρ/ρ. Сукупність числа Ga і Δρ/ρ дає нове число подібності, яке прийнято називати числом Архімеда
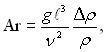 (5.38)
(5.38)
яке характеризує відношення підйомних сил до сил в’язкості.
Якщо різниця густин рідини визначається різницею температур ΔТ, то симплекс Δρ/ρ можна представити через коефіцієнт об’ємного розширення рідини
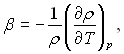
вважаючи його постійним в даному інтервалі температур, у виді Δρ/ρ = βΔТ. У цьому разі число Архімеда приймає наступний вигляд:
![]() (5.39)
(5.39)
і носить назву числа Грасгофа.
Відношення числа Пекле до числа Рейнольдса носить назву числа Прандтля:
![]() (5.40)
(5.40)
Число Прандтля містить у собі тільки фізичні параметри середовища, і тому є безрозмірним фізичним параметром. Для газів воно практично не залежить ні від температури, ні від тиску, величина його визначається атомністю газу і недалека від одиниці: для одноатомних газів Pr = 0,67; для двохатомних Pr = 0,72; для трьохатомних Pr = 0,8; для багатоатомних Pr = 1,0.
Для крапельних рідин величина числа Прандтля перевищує одиницю і у випадку дуже в’язких рідин може досягати великих значень. Так для цукрового розчину з вмістом цукру 86% при температурі 40 °С Pr = 520000. Виключення складають рідкі метали, які характеризуються дуже малими значеннями числа Прандтля (порядку 10–2...10–3).
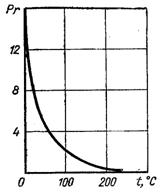
Рис.5.3. Залежність числа Прандтля від температури води на лінії насичення
Число Прандтля для крапельних рідин сильно залежить від температури. Так для води (рис.5.3) при температурах від 0 до 180 °С число Прандтля змінюється відповідно від 13,7 до 1,0, що зв’язано зі зменшенням в’язкості і збільшенням теплопровідності у цій області температур. При температурах 130...310 °С значення числа Pr для води змінюється незначно і близькі до одиниці. Характер залежності Pr від температури різко змінюється при тисках, близьких до критичних.
Інколи замість не визначального числа Нуссельта використовують число Стентора, яке представляє собою комбінацію чисел Nu, Re, Pr у вигляді
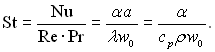 (5.41)
(5.41)
Із формули (5.41) виходить, що
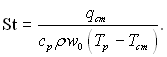
Отже, число Стентора представляє собою відношення теплового потоку в стінку до того конвективного потоку, який може бути перенесеним потоком рідини при зменшенні її температури від Тр до Тст.
При розгляді теплообміну при високих швидкостях (w0 > wзв/4) необхідно враховувати стисливість середовища. У цьому випадку із системи рівнянь методом теорії подібності можна отримати додаткове число подібності, яке містить число подібності Маха М = w0/wзв і відношення питомих теплоємностей k = cp/cV . Число Маха представляє собою відношення швидкості потоку до швидкості розповсюдження звуку в даному середовищі і характеризує стисливість середовища.
Система безрозмірних диференціальних рівнянь конвективного теплообміну містить у собі дві групи змінних: незалежних Nu, T|, w|x, w|у, w|z, Eu. Залежні змінні однозначно визначаються значеннями змінних при певних значеннях визначальних чисел подібності Re, Pr, Fr, Gr, Fo, Ho, до числа яких можуть входити і параметричні числа подібності.
Отже, рівняння подібності можна звести до наступної форми запису:
![]()
![]()
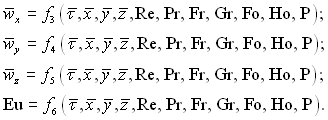 (5.42)
(5.42)
В окремих випадках деякі величини (змінні чи числа подібності) можуть не входити до рівнянь подібності. У деяких випадках, коли важливо знати середні значення коефіцієнта тепловіддачі за всією поверхнею і за весь період процесу до рівнянь подібності не входять значення координат поверхні і часу τ|, x|, y|, z|. Якщо масштаби τ0 для часу зміни температурного і швидкісного полів однакові, то замість числа Фур’є і гомохронності в рівняннях будуть присутні тільки одне з них.
При розгляді усталеного процесу відсутні числа Fo і Ho. Коли сила тяжіння дуже мала в порівнянні з інерційною силою, з визначальних чисел подібності випадає число Фруда.
Під час вимушеного турбулентного руху в більшості випадків можна знехтувати впливом вільної конвекції і тоді з числа визначальних чисел подібності випадає число Грасгофа. Під час природного, вільного руху рідини з визначальних чисел подібності залишаються тільки числа Грасгофа і Прандтля.
Таким чином, для найбільш характерних стаціонарних випадків конвективного теплообміну рівняння подібності для коефіцієнта тепловіддачі мають наступний вид:
У випадку газів однакової атомності, для яких число Pr однакове і постійне, то рівняння подібності не буде містити цього числа подібності.
Під час розгляду більш складних процесів конвективного теплообміну, наприклад теплообміну при зміні агрегатного стану, теплообміну при течії газу з надзвуковими швидкостями, теплообміну на проникливій поверхні, отримана система чисел подібності повинна доповнюватися новими числами подібності, які відображають особливості розглядуваного процесу.
5.5. Метод аналізу розмірності
Необхідною передумовою теорії подібності є наявність математичного опису розглядуваного явища у вигляді диференціальних рівнянь і умов однозначності, на підставі яких знаходиться загальний вигляд рівнянь подібності. Але у ряді випадків вивчення того чи іншого явища може бути настільки складним, що для нього неможливо створити замкнену систему диференціальних рівнянь.
Вид чисел подібності, суттєвих для явища, і загальний вигляд рівняння подібності можна підібрати і без складання диференціальних рівнянь. Це можна зробити за допомогою метода аналізу розмірності. У цьому випадку необхідно мати повний перелік фізичних величин, суттєвих для розглядуваного явища, тобто тих величин, які ввійшли б у диференціальні рівняння і умови однозначності, якби математичний опис процесу був відомим. Перелік фізичних величин можна скласти на базі загальних фізичних міркувань і набутого досвіду.
Величини, числове значення яких залежить від прийнятої системи одиниць виміру, називаються розмірними. Довжина, швидкість, сила, час, енергія, температура та ін. можуть служити прикладом розмірних величин. Величини, числові значення яких не залежать від використовуваної системи одиниць виміру називаються безрозмірними. Поділ величин на розмірні і безрозмірні є умовним. Наприклад, прискорення зазвичай розглядається як розмірна величина, розмірність якої є довжина розділена на час в квадраті. Якщо прискорення вільного падіння (9,81 м/с2) вибрати як одиницю виміру, тоді довільне прискорення буде вимірюватися відношенням його величини до величини прискорення вільного падіння і не буде вимірюватися при переході від одних одиниць виміру до інших. Це відношення називається перевантаженням і є безрозмірною величиною.
Залежність одиниці виміру довільної величини від одиниці виміру основних величин можна представити у вигляді формули, яка називається формулою розмірності. У різних системах одиниць виміру розмірності для одної і тієї ж величини може мати різний вигляд.
Під розмірністю фізичної величини слід розуміти вираз, який відображає зв’язок розглядуваної величини з основними одиницями системи, якщо коефіцієнт пропорціональності у цьому виразі дорівнює безрозмірній одиниці. Розмірність фізичної величини залежить не тільки від природи цієї фізичної величини, але і від вибору системи одиниць.
Досвід показує, що більшість розмірностей можна виразити через розмірності основних величин. Розмірності, які виражаються згідно з певними фізичними рівняннями через основні величини, називають похідними величинами. У теорії теплообміну за основні приймаються: довжину (розмірність L), температуру (розмірність Θ), час (розмірність Т) і масу (розмірність М). Усі інші розмірності можна виразити через них.
Основним положенням, яке використовується в методі аналізу розмірності при знаходженні кількості і виду чисел подібності, є аксіома про те, що додаватися і відніматися можуть тільки величини і комплексні величини, які мають однакову розмірність, а також та обставина, що одні розмірності виражаються через інші у вигляді їх добутку з відповідними степенями. На цих засадах виявляється, що довільна фізична величина N якщо вона є функцією величин А, В, С,..., то ця залежність може бути представлена у вигляді добутку цих розмірностей в деяких степенях а, b, c,…, і т. д.
N = f(A, B, C, D,…) = kAaBbCcDd, (5.43)
де k – постійний коефіцієнт.
У такому випадку, якщо виразити кожну з розмірностей (A, B, C, D,…) через розмірності основних величин, можна виявити відповідні величини показників степеня а, b, c, d,… і забезпечити однаковість розмірностей лівої і правої частин рівняння. Для цього в отриманому рівнянні розмірностей показник степеня біля певної розмірності в лівій частині рівняння повинен бути рівним сумі показників степені у відповідній розмірності в правій частині. Ця обставина робить можливим об’єднати фізичні величини в безрозмірні комплекси – числа подібності. При цьому виходить, що між кількістю фізичних величин і кількістю безрозмірних комплексів існує певне співвідношення, яка визначається π-теоремою.
Метод отримання чисел подібності і зміст π-теореми можна ілюструвати наступним чином. Виражаючи кожну з розмірностей рівняння (5.43) через розмірності L, T, Θ, M, можна записати:
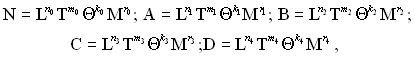
де n, m, k, r – показники степеня біля відповідних розмірностей основних величин, через які виражені розмірності N, A, B, C, D. Підставляючи отримані вирази в рівняння (5.43), отримаємо:
![]() (5.44)
(5.44)
На підставі рівності показників степені біля відповідних розмірностей в лівій і правій частинах рівняння можна скласти наступну систему рівнянь для степені:
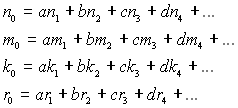 (5.45)
(5.45)
Отже, кількість рівнянь для степенів дорівнює числу основних величин т. Число невідомих степенів у системі a, b, c, d,… дорівнює числу членів у правій частині рівняння і на одиницю менше загальної кількості всіх фізичних величин, суттєвих для явища п, тобто п – 1. Тому що в загальному випадку п – 1 > m, то число невідомих величин у даній системі рівнянь виходить більшою за число рівнянь і тому п – т – 1 степенів не можуть бути визначеними з цієї системи рівнянь. Але система рівнянь (5.45) дозволяє виразити певну кількість степенів, рівну числу рівнянь, через решту п – т – 1 степенів, які не можуть бути визначеними.
Після підстановки усіх степенів, які виражають невизначені степені, в рівняння (5.43) отримаємо рівняння де всі розмірності окажуться чи в першому степені, чи у степенях, через які виражаються інші степені. Фізичні величини, які будуть у першому степені, серед яких буде і шукана величина N, утворюють не визначальне число подібності в лівій частині рівняння. Інші фізичні величини з однаковими степенями можна згрупувати в безрозмірні комплекси – визначальні числа подібності в правій частині рівняння.
Кількість визначальних чисел подібності буде дорівнювати числу невідомих степенів п – т – 1. Загальна кількість чисел подібності, один з яких не визначальний, на одиницю більше ніж визначальних п – т.
Отриманий результат складає зміст π-теореми, яка стверджує, що число безрозмірних комплексів, які характеризують процес, дорівнює числу всіх фізичних величин, суттєвих для процесу, мінус число основних розмірностей п – т. Нульове чи від’ємне значення різниці п – т означає, що сукупність розглядуваних фізичних величин не може бути приведена до безрозмірного виду. Ця сукупність величин не задовольняє умови аналізу розмірностей. У ній відсутні певні величини, які дозволяють привести цю систему величин до безрозмірного вигляду. Такі системи називаються неповними. При складанні системи визначальних параметрів завжди слід провіряти повноту системи. При п – т = 1 рівняння подібності матиме тільки одне не визначальне число подібності, яке буде сталою величиною. Умова п – т = 1 викликає інтерес, тому що зводить рішення розглядуваної задачі до знаходження одного постійного множника.
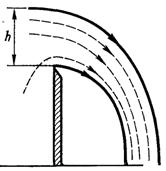
Рис.5.4. Рух рідини через водозлив
Як приклад розглянемо задачу про течію рідини через водозлив (рис.5.4). Усталений рух рідини через водозлив повністю визначається параметрами ρ, g, h. Витрати рідини G через водозлив в одиницю часу можуть бути функцією тільки цих параметрів. Вибираючи за основні розмірності L, T, M (довжину, час, масу), отримаємо п – т = 1. Таким чином, у розглядуваних умовах у відповідності з π-теоремою повинно бути тільки одне безрозмірне число подібності, яке включає в себе шукані витрати рідини G
Єдиною безрозмірною комбінацією з вихідних величин є
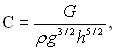 (5.46)
(5.46)
значення числа подібності С можна визначити експериментальним шляхом.
У тому випадку, коли
п – т = 2, (5.47)
безрозмірне рівняння подібності містить тільки два безрозмірних числа подібності: π1 і π2, тобто
F(π1, π2) = 0. (5.48)
Отже
π1 = Ф (π2). (5.49)
Якщо п – т = 3, то безрозмірне рівняння подібності буде містити три числа подібності і т. д.
Як приклад розглянемо отримання форми рівняння подібності для визначення коефіцієнта тепловіддачі у випадку вимушеного руху рідини в трубі. На підставі загальної фізичної уяви вважаємо, що коефіцієнт тепловіддачі α залежить від діаметра труби D, швидкості потоку w0, густини ρ, в’язкості μ, теплопровідності λ, питомої теплоємності рідини с, тобто
α = f(D, w0, ρ, μ, λ). (5.50)
Таким чином, загальна кількість фізичних величин дорівнює семи: п = 7. Для аналізу розмірності цю залежність можна представити так:
![]() (5.51)
(5.51)
Усі розмірності величин, які входять у рівняння, можна виразити через розмірності основних величин L, T, Θ, M у такому виді:
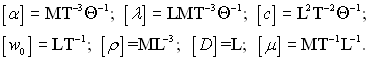
Підставляючи ці вирази в рівняння (5.51), отримаємо рівняння розмірності в виді:
![]() (5.52)
(5.52)
З умови рівності степенів при відповідній розмірності в лівій і правій частинах рівняння можна записати наступну систему рівнянь для показників степені:
при L 0 = a + b – 3c – d + e + 2f; (5.53)
при T –3 = –b – d – 3e – 2f; (5.54)
при М 1 = c + d + e; (5.55)
при Θ –1 = –e – f. (5.56)
Ця система, яка складається з чотирьох рівнянь (т = 4), містить в собі шість невідомих показників степені (п – 1) = 6. Отже, для показника степеня не можуть бути визначеними (п – т – 1 = 2). Приймаючи за такі, що не можуть бути визначеними, степені с і f можна виразити через інші (a, b, d, e) таким способом:
Далі, підставляючи відповідні показники степеня в рівняння (5.51), отримаємо вираз для коефіцієнта тепловіддачі у наступному виді:
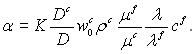 (5.57)
(5.57)
Об’єднуючи величини з однаковими показниками степені, отримуємо рівняння в безрозмірному вигляді:
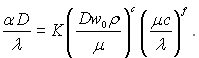 (5.58)
(5.58)
Отримані безрозмірні комплекси можна представити у вигляді відомих чисел подібності:
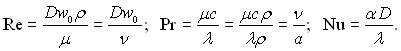
Отже, рівняння подібності для розглядуваного випадку тепловіддачі при вимушеному русі в трубі можна записати так:
![]() (5.59)
(5.59)
Отримане рівняння знаходиться у відповідності з π-теоремою: число чисел подібності (Nu, Re, Pr) дорівнює різниці між числом розмірних параметрів п = 7 (α, D, w0, ρ, μ, λ) і числом основних розмірностей т = 4 (L, Θ, T, M). Константа К і невідомі показники степені при певних числах подібності с і f в отриманому рівнянні визначаються експериментальним шляхом.
Числа подібності, отримані методом аналізу розмірності, не завжди за формою співпадають з основними числами подібності, отриманими на засадах теорії подібності. Але системи чисел подібності, отримані різними методами, еквівалентні між собою.
Таким чином, теорія подібності і аналіз розмірностей є, за своєю сутністю, різними методами одної і тієї ж системи дослідження, які ґрунтуються на використанні узагальнених безрозмірних змінних, різниця між якими обумовлена тільки об’ємом попередніх знань про досліджуваний процес. Для застосування теорії подібності необхідний великий об’єм попередніх знань достатній для виведення рівнянь, які визначають процес. Якщо застосування теорії подібності можливе, то їй варто віддати перевагу. В рамках теорії подібності виявляється фізичний зміст чисел подібності. Якщо математична постановка задачі неможлива, то застосування аналізу розмірностей стає неминучим. У цьому випадку не завжди є впевненість у безпомилковому складанні переліку суттєвих для процесу величин і правильності прийнятої системи розмірностей. У тих випадках, коли перелік величин, суттєвих для процесу, і їх зв’язок з початковими розмірностями установлено точно, метод аналізу розмірності забезпечує результати, еквівалентні результатам, отриманим за допомогою теорії подібності.