




Розділ 6. КОНВЕКТИВНИЙ ТЕПЛООБМІН ВИМУШЕНОМУ РУСІ РІДИНИ
6.1. Основи теорії пограничного шару
6.1.1.Особливості руху в’язкої рідини при великих числах Re. Пограничний шар
Під час руху в’язкої рідини з великими числами Re вплив в’язкості проявляється неоднаково біля стінки і на відстані від неї.
Біля стінки внаслідок адгезії (прилипання) рідини до твердої стінки виникають суттєві поперечні градієнти швидкості і, як наслідок, значні дотичні напруги. При поступовому віддаленні від стінки зміна повздовжньої швидкості по нормалі до поверхні тіла зменшується і дія сил в’язкості стає зникаюче малою вже на порівнянно невеликій відстані від стінки.
Таким чином, під час руху рідини з великими числами Re весь потік можна розбити на дві області: область динамічного пограничного шару, де вплив в’язкості суттєвий і зовнішня область потенціальної течії, де вплив в’язкості дуже малий. Чим більше число Re потоку, тим більша відносна величина сил інерції у порівнянні з силами в’язкості, тим тонкіший шар і, навпаки, зі збільшенням ролі сил в’язкості відбувається потовщення пристінної області течії.
Поділ потоку на пограничний шар і зовнішню течію значно спрощує аналіз течії в цілому, тому що дозволяє розглядати кожну з областей течії окремо. Крім цього, за цих умов у зовнішній течії інерційні сили переважають сили в’язкісного тертя, тому для опису руху можна користуватися рівняннями для ідеальної рідини.
Математичний опис руху рідини у пограничному шарі також значно спрощується, а отримані наближені рівняння піддаються інтегруванню.
Роздільний метод спрощених рівнянь з подальшим змиканням отриманих рішень для пограничного шару і зовнішнього потенціального потоку дозволяє аналітично отримати усі необхідні характеристики потоку в цілому.
Якщо між потоком рідини і поверхнею тіла відбувається теплообмін чи дифузія, то за аналогією з динамічним пограничним шаром біля поверхні обтікання тіла утворюється тепловий чи дифузійний пограничний шар, тобто область біля стінки, в якій температура чи концентрація домішок змінюються від значень біля стінки до відповідних величин у зовнішньому потоці.
У пограничному шарі швидкість, температура і концентрація домішок асимптотично наближаються до своїх значень у потенціальному потоці, тому за товщину пограничного шару приймають ту відстань по нормалі до поверхні, де величина швидкості, температури чи концентрації відрізняються на 1% від відповідної величини у зовнішньому потоці.
Не дивлячись на свою незначну в порівнянні з характерними зовнішніми розмірами в потенціальному потоці, пограничний шар відіграє основну роль в процесах динамічної і теплової взаємодії потоку рідини з поверхнею.
6.1.2. Диференціальні рівняння динамічного, теплового і дифузійного пограничних шарів
Вперше систему диференціальних рівнянь динамічного пограничного шару отримав в 1904 р. відомий аеродинамік Л.Прандтль, виконавши порівняльну оцінку членів рівнянь Нав’є-Стокса і відкинувши члени другого порядку малості.
Розглянемо, слідуючи ідеям Прандтля, випадок стаціонарного плоского пограничного шару стислої рідини при відсутності об’ємних сил і процесів дифузії. За цих умов система рівнянь Нав’є-Стокса і рівняння енергії (див. розділ 4) приймає вид:
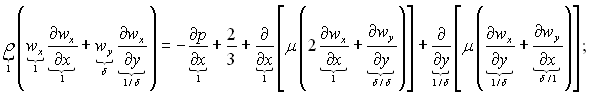
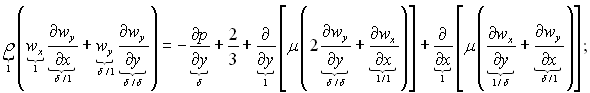 (6.1)
(6.1)
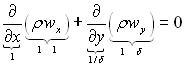 ; (6.2)
; (6.2)
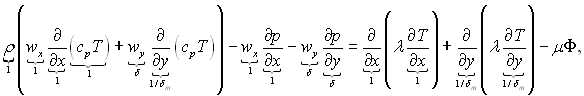 (6.3)
(6.3)
Де Ф – дисипативна функція рівна
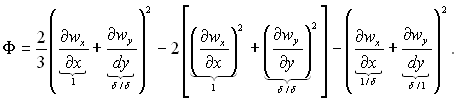
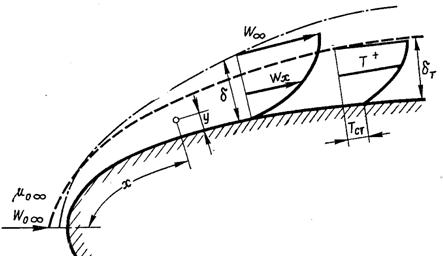
Рис.6.1. Схема пограничного шару на криволінійній поверхні
Перетворимо рівняння руху (6.1), враховуючи відмічені раніше властивості пограничного шару – малі поперечні розміри і швидкості в порівняння з повздовжніми. Вважаємо, що товщина пограничного шару δ мала в порівнянні з відстанню х (рис.6.1). Порядок величин wx і х приймаємо за одиницю, тоді відстань у~δ. З рівняння нерозривності потоку (6.2) виходить, що поперечна швидкість wy також має порядок δ, якщо порядок густин прийняти рівним одиниці. Оскільки нами прийнято, що wx і х порядку одиниці, то похідні дwx/дx і д2wx/дx2 повинні бути того ж порядку, а похідні дwx/ду і д2wx/ду2 – порядку 1/δ і 1/δ2 відповідно.
Тримаючи це на увазі, виконаємо оцінку членів рівняння (6.1). Отримані порядки підпишемо під відповідними членами рівнянь. Розглянемо спочатку перше з рівнянь руху. Очевидно, що перших два члена, записані в лівій частині, мають порядок одиниці. Щоб визначити порядок др/дх, згадаємо, що у випадку плоскопаралельного руху рідини з великими числами Re зовнішня область потенціальної течії описується рівнянням руху ідеальної рідини
![]() (6.4)
(6.4)
Градієнт тиску не може змінити свого порядку із-за наявності тонкого пограничного шару, тому порядок величини др/дх також можна приймати рівним одиниці.
Повертаючись до правої частини першого рівняння руху, зауважимо, що зі всіх членів, які містять в собі в’язкість, можна залишити тільки 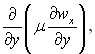 який має порядок 1/δ. Але цей член повинен бути одного порядку з іншими конвективними членами, які мають порядок одиниці. Остання умова можлива в тому випадку, коли в’язкість
μ має порядок
δ2. Це в свою чергу говорить про те, що пограничний шар може існувати тільки при обтіканні поверхні потоком з дуже малою в’язкістю, чи, що те саме, з великими числами Re.
який має порядок 1/δ. Але цей член повинен бути одного порядку з іншими конвективними членами, які мають порядок одиниці. Остання умова можлива в тому випадку, коли в’язкість
μ має порядок
δ2. Це в свою чергу говорить про те, що пограничний шар може існувати тільки при обтіканні поверхні потоком з дуже малою в’язкістю, чи, що те саме, з великими числами Re.
З другого рівняння слідує, що похідна др/ду повинна бути порядку δ, тому що всі інші члени цього рівняння мають такий же чи ще більш низький порядок і зміною тиску поперек пограничного шару можна знехтувати. Тобто тиск поперек пограничного шару залишається сталим і рівним тиску на зовнішній границі пограничного шару.
Таким чином, зберігаючи в рівнянні Нав’є-Стокса члени одного і того ж порядку, замість рівнянь (6.1) і (6.2) отримаємо наступну систему рівнянь, яка описує рух в’язкої рідини в плоскому усталеному пограничному шарі:
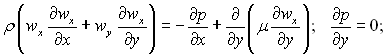 (6.5)
(6.5)
![]() (6.6)
(6.6)
з граничними умовами у = 0→wx = 0; wy = 0; y = δ→wx = w∞.
Рівняння енергії в пограничному шарі (6.3) також спрощується. Позначивши товщину теплового пограничного шару через δт оцінимо порядок членів в рівнянні енергії.
Перші два члена в лівій частині рівняння енергії згідно з попередніми оцінками – величини порядку одиниці. Членом wyдр/ду можна знехтувати в порівнянні з wхдр/дх, тому що згідно (6.5) тиск поперек пограничного шару залишається практично усталеним. Між всіма членами, які містять в’язкість, варто зупинитися тільки на
μ(дwx/ду)2, який має порядок
1/δ2, тому що інші члени мають
значно менший порядок. Для того щоб член, який містять в собі теплопровідність,
був одного порядку з іншими членами рівняння енергії, необхідно, щоб
теплопровідність була порядку
δт2. Це означає, що тепловий пограничний шар існує в рідинах з малим значенням теплопровідності. У цьому разі членом 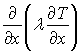 можна знехтувати в порівняння з членом
можна знехтувати в порівняння з членом 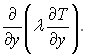
Таким чином, залишаючи в рівнянні (6.3) тільки члени порядку одиниці, отримаємо рівняння енергії плоского в’язкого стисливого пограничного шару
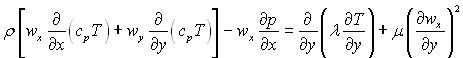 (6.7)
(6.7)
з граничними умовами у = 0 → Т = Тст; у = ∞ → Т =Т∞.
Для ідеального газу ентальпія становить h = cpT і рівняння (6.7) можна записати через ентальпію:
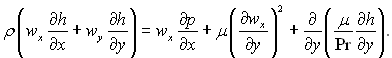 (6.8)
(6.8)
Рівняння (6.8) має простий фізичний зміст: конвективна зміна ентальпії дорівнює сумі потужності сил тиску, теплоти, яка виникає за рахунок дисипації енергії, и теплоти, що підводиться за рахунок теплопровідності.
Помноживши кожний член рівняння (6.5) на wx і додавши почленно з (6.7), отримаємо рівняння для повної ентальпії пограничного шару в наступному вигляді:
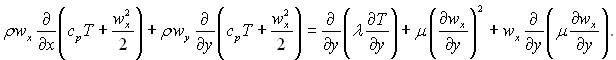 (6.9)
(6.9)
Але
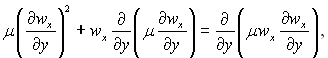
тоді рівняння (6.9) можна перетворити до наступного вигляду:
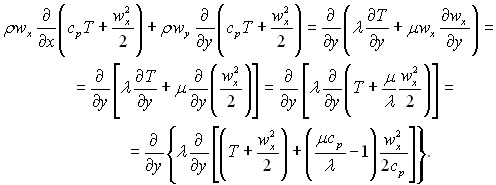
Вважаючи питому теплоємність ср сталою поперек пограничного шару, що повністю допустимо для ідеального газу, і вводячи безрозмірне число Прандтля, отримуємо в кінцевому вигляді рівняння енергії:
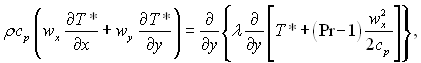 (6.10)
(6.10)
де 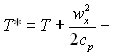 температура гальмування.
температура гальмування.
Рівняння (6.2), (6.5)...(6.7) і рівняння стану ідеального газу утворюють систему рівнянь плоского симетричного пограничного шару і містять у собі такі перемінні величини: wx, wy, p, ρ, T, μ, λ, cp. Ця система замикається трьома додатковими залежностями: динамічною в’язкістю, теплопровідністю і питомою теплоємністю в залежності від температури.
6.1.3. Система рівнянь плоского стисливого пограничного шару з урахуванням дифузійних і хімічних реакцій
Отримані рівняння пограничного шару можна узагальнювати на випадки руху суміші різнорідних і реагуючих газів.
У випадку реакцій, які можуть відбуватися в системі, виникають чи зникають окремі компоненти суміші, тому рівняння нерозривності потоку для і-го компоненту суміші записується так
![]() (6.11)
(6.11)
де ρ, wxi, wyi – густина і відповідні компоненти швидкості і-го компонента відповідно; ті – секундна масова швидкість утворення і-го компонента віднесена до одиниці об’єму.
Але при цьому для суміші газів, які реагують між собою, рівняння нерозривності потоку зберігає свій попередній вид
![]() (6.12)
(6.12)
якщо компоненти масової швидкості визначаються умовою
![]()
Окрім цього, виконуються умови передбачені законом збереження маси для суміші.
![]() (6.13)
(6.13)
Рівняння руху, яке записується для суміші газів, також зберігає свою попередню форму:
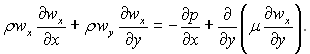 (6.14)
(6.14)
Те саме можна сказати і про рівняння стану
р = ρRT, (6.15)
якщо вважати, що
![]() (6.16)
(6.16)
де Сі = ρі, ρ – масова частка і-го компонента.
Основні особливості процесів з реагуючими сумішами відображаються рівняннями, які описують тепло- і масоперенос (рівняння дифузії і енергії).
Рівняння дифузії і-го компонента отримуємо з рівняння нерозривності потоку (6.11) таким способом: швидкість дифузії і-го компонента wi* визначаємо як різницю швидкостей руху компонента в суміші wi* = wi – w. Заміняючи в рівнянні (6.11) швидкість руху сумою швидкостей дифузії і суміші, отримаємо:
![]() (6.17)
(6.17)
За основним законом дифузії, швидкість дифузії визначається через градієнти масових часток температури і тиску наступним чином:
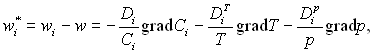 (6.18)
(6.18)
де Di, DiT, Dip – коефіцієнти масової дифузії, термодифузії і бародифузії, відповідно. Підставляючи співвідношення (6.18) в рівняння (6.17) і враховуючи рівняння (6.12), після перетворень отримуємо
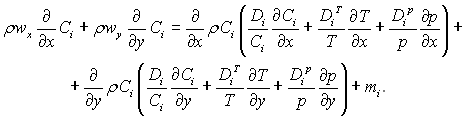
Для дифузійного пограничного шару це рівняння можна спростити, відкинувши перший член в його правій частині, який має менший порядок у порівнянні з іншими членами. Крім цього, роль бародифузії у пограничному шарі мала, тому що др/ду ≈ 0, і нею теж можна знехтувати.
Таким чином, рівняння дифузії і-го компоненту в плоскому стисливому пограничному шарі має наступний вигляд
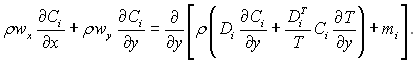 (6.19)
(6.19)
Для отримання рівняння балансу теплоти використаємо рівняння (6.8). Підвід теплоти конвекцією визначається так само, як і в випадку руху однорідного газу, якщо вважати, що ентальпія газу, який реагує, визначається за правилом змішування:
![]() (6.20)
(6.20)
Але в рівнянні енергії необхідно врахувати два додаткових джерела теплоти, які зв’язані як з утворенням нових компонент, так і з процесами дифузійного переносу. Процес виділення чи поглинання теплоти при утворенні нових компонент приводить до приєднання до правої частини рівняння (6.8) члена
![]() (6.21)
(6.21)
який згідно з рівнянням (6.11) набуває вигляду
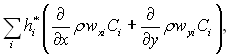 (6.22)
(6.22)
де hi* – теплота утворення і-го компонента.
За визначенням, швидкість дифузії і-го компонента дорівнює векторній різниці абсолютних швидкостей компонента і суміші, тому потік теплоти за рахунок дифузії можна виразити у формі вектора з проекціями на осі х і у:
![]() (6.23)
(6.23)
Отже, другий додатковий член в рівнянні енергії, який відповідає дифузійному переносу тепла, визначається дивергенцією, взятою зі зворотним знаком, суми векторів потоку теплоти, викликаних окремими компонентами,
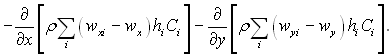 (6.24)
(6.24)
З урахуванням (6.22) і (6.24) рівняння енергії (6.7) набуває виду
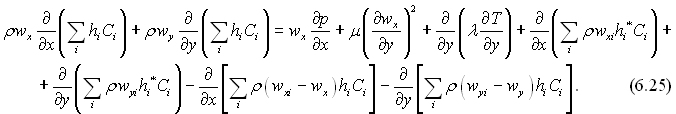
Виконавши тотожні перетворення
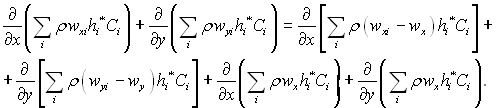
перепишемо рівняння (6.25)
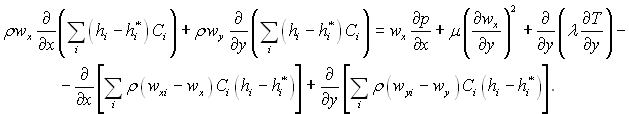 (6.26)
(6.26)
Нехтуючи в рівнянні (6.26) передостаннім членом, отримаємо рівняння енергії пограничного шару з урахуванням хімічних реакцій:
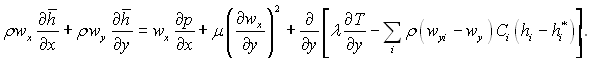 (6.27)
(6.27)
У цьому рівнянні ![]() повна ентальпія суміші. Підставляючи вираз (6.18) для швидкості дифузії в напрямку осі у (без урахування бародифузії) у рівняння (6.27), отримаємо кінцевий вираз
повна ентальпія суміші. Підставляючи вираз (6.18) для швидкості дифузії в напрямку осі у (без урахування бародифузії) у рівняння (6.27), отримаємо кінцевий вираз
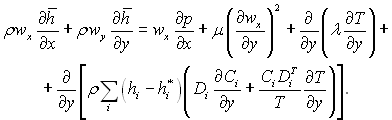 (6.28)
(6.28)
Це рівняння енергії пограничного шару, яке записане через ентальпію, можна привести до рівняння, яке містить у собі, як основний параметр, температуру. Зауважимо, що
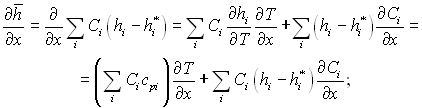
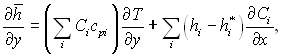
і позначивши ![]() перепишемо рівняння енергії:
перепишемо рівняння енергії:
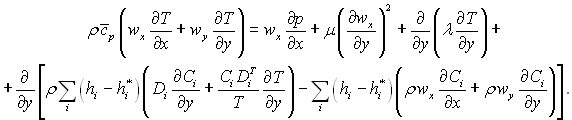 (6.29)
(6.29)
Замінимо в цьому виразі останній член, використовуючи рівняння (6.19) і виконуючи скорочення:
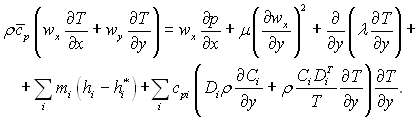 (6.30)
(6.30)
Рівняння енергії для суміші реагуючих газів, яке записується через повну ентальпію буде
![]() (6.31)
(6.31)
мати наступний вигляд:
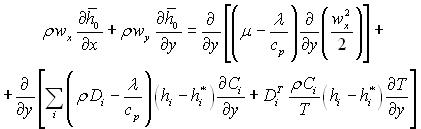 (6.32)
(6.32)
Введемо в рівняння балансу масові частки (6.19) і в рівняння енергії пограничного шару у формі (6.32) числа Прандтля, Шмідта, Люіса (останні аналогічні числу Прандтля і є безрозмірними фізичними параметрами):
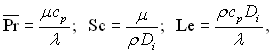 (6.33)
(6.33)
де ![]() так названа заморожена питома теплоємність суміші, отримуємо для усталеного плоского стисливого пограничного шару систему рівнянь, які враховують наявність хімічних реакцій (без урахування переносу маси за рахунок термодифузії):
так названа заморожена питома теплоємність суміші, отримуємо для усталеного плоского стисливого пограничного шару систему рівнянь, які враховують наявність хімічних реакцій (без урахування переносу маси за рахунок термодифузії):
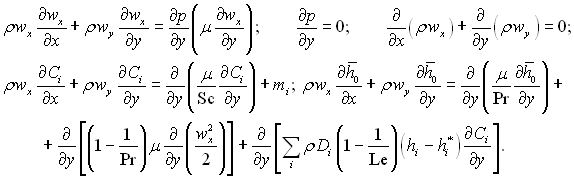 (6.34)
(6.34)
Зазвичай ця система рівнянь розв’язується за наступними граничними умовами:
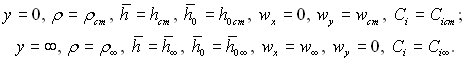 (6.35)
(6.35)
Виконаємо тепер порівняльну оцінку товщини динамічного, теплового і дифузійного пограничного шару. Для цього перепишемо диференціальні рівняння пограничного шару в безрозмірній формі.
За масштаб фізичних величин виберемо наступні параметри:
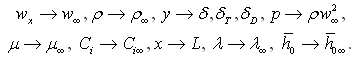
Рівняння руху після приведення до безрозмірного виду буде
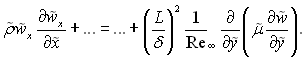 (6.36)
(6.36)
Тут і в подальшому тильдою позначені безрозмірні величини, наприклад ![]()
Всі члени рівняння (6.36) будуть мати один і той же порядок тільки за умови, що
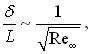 (6.37)
(6.37)
де ![]()
Таким чином, доказане основне припущення, яке покладено в основу виводу рівнянь пограничного шару, що при течії рідини з великими числами Re товщина пограничного шару невелика і має порядок ![]()
Аналогічним чином перетворюється рівняння енергії:
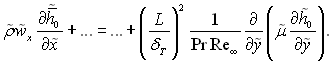
Якщо обидва члени мають один і той же порядок, то
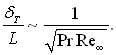 (6.38)
(6.38)
З виразів (6.37) і (6.38) отримаємо порядок співвідношення між товщиною теплового і динамічного пограничного шару:
![]() (6.39)
(6.39)
Співвідношення (6.39) показує, що в газах і рідких металах, для яких Pr<1, тепловий пограничний шар товщай динамічного, а в рідинах (Pr>1) δТ < δ.
Перетворивши до безрозмірного вигляду рівняння дифузії, матимемо
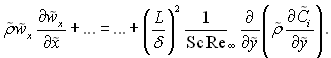
Обидва члени рівняння дифузії мають однаковий порядок, якщо
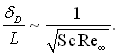 (6.40)
(6.40)
Згідно рівнянню (6.37) знайдемо
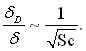 (6.41)
(6.41)
У табл.6.1 наведені значення чисел Шмідта для суміші різних газів з повітрям.
Таблиця 6.1. Числа Шмідта для малих концентрацій різних газів в повітрі
|
Газ |
Віднос-на мо-лекуку-лярна маса |
Число Шмі-дта Sc |
Газ |
Віднос-на мо-лекуку-лярна маса |
Число Шмі-дта Sc |
Водень Метан Аміак Водяна пара Азот Етан Кисень Метанол Двоокис вуглецю Пропан Етанол Ацетон Бутан Ацетатна кислота п-Пропінол Двоокис сірки Хлор |
2,016 16,04 17,03 18,016 28,02 30,07 32,00 32,04 44,01 44,09 46,07 58,08 58,12 60,05 60,09 64,06 70,90 |
0,22 0,84 0,61 0,60 0,98 1,22 0,74 1,00 0,96 1,51 1,30 1,60 1,77 1,24 1,55 1,28 1,42 |
Пентан п-Метанол Етиловий ефір п-Бутанол Сірчаний вуглець Бензин Етилацетат Толуол Фосген Хлорбензол п-Пропілацетат п-Октан Нафталін Чотирьоххлористий вуглець Бромбензол Хлорпікрин Бромід етилен |
72,15 74,08 74,12 74,12 76,13 78,11 88,10 92,13 98,92 102,13 112,56 114,22 128,16 153,54 157,02 164,39 187,88 |
1,97 1,57 1,70 1,88 1,48 1,71 1,84 1,86 1,97 1,97 2,13 2,62 2,57 2,13 1,97 2,13 1,97 |
З точністю ±30% залежність числа Шмідта від молекулярної маси газу за його концентрації в повітрі, прямуючої до нуля, можна визначити по формулі
![]()
Вплив концентрації можна також урахувати по формулі
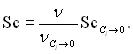
Для газів, які мають відносну молекулярну масу Мі < 32, число Шмідта Sc < 1 і відповідно рівнянню (6.41) дифузійний пограничний шар товщий динамічного. Як що Мі > 32, то δD < δ.