6.1.4. Потрійна аналогія

Рівняння руху і енергії пограничного шару (6.34) стають тотожними за умови Pr = Le = Sc = 1 і др/дх = 0. Можна показати, що у цьому випадку рівняння дифузії стає тотожним рівнянню руху і енергії, якщо ввести у рівняння дифузії і енергії замість масової частки і-го компонента С_і так звану повну концентрацію (див. § 6.2) хімічного елементу суміші СС̃_j.

Зв’язок між С̃_j і С_і виражається залежністю:

У цій залежності r_j,I – масова частка j-го компонента в і-му компоненті.

У разі, коли не відбуваються внутрішні перетворення в пограничному шарі, то масові частки окремих хімічних елементів не змінюються. Отже, якщо в рівнянні дифузії і енергії системи (6.34) замінити С_і на С̃, то в правій частині рівняння дифузії перетвориться в нуль. Тоді рівняння дифузії, руху і енергії стають тотожними. Наслідком цього за подібності граничних умов, тобто при w_cm = 0, h̃_0cm = const, C̃_jcm = const, повинна бути подібність полів швидкостей, полів концентрацій і повної ентальпії гальмування:

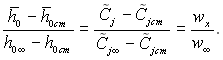(6.42)

Тому що

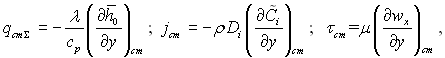(6.43)

то з рівнянь (6.42) і (6.43) виходить, що для розглядуваних умов

(6.44)

де

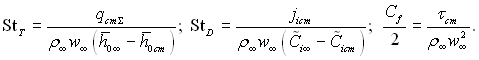
Рівняння (6.44) широко використовується в інженерній практиці під час розрахунків процесів теплообміну і масообміну.

6.1.5. Інтегральні співвідношення імпульсів, енергії і дифузії

Отримані диференціальні рівняння пограничного шару простіші за відповідні повні диференціальні рівняння руху, енергії і дифузії в’язкої рідини. Але точний розв’язок системи диференціальних рівнянь пограничного шару можливий тільки для дуже обмеженої кількості законів, якими задаються швидкості зовнішньої течії при граничних умовах на стінці, коли диференціальні рівняння пограничного шару в частинних похідних можна привести до звичайних диференціальних рівнянь.

У цьому випадку велике значення набувають наближені методи вирішення названих рівнянь, які ґрунтуються на застосуванні інтегральних співвідношень імпульсів, енергії і маси.

Інтегральне рівняння кількості руху отримуємо з рівнянь руху (6.5), інтегруючи по товщині пограничного шару і отримуємо закон збереження кількості руху рідини, яка тече через даний переріз пограничного шару.

Використовуючи рівняння (6.4) і (6.2), перепишемо рівняння руху (6.5) у такій формі:

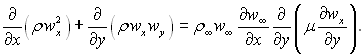
Помножимо всі члени рівняння нерозривності потоку (6.2) на значення швидкості на зовнішній границі пограничного шару w_∞, отримаємо

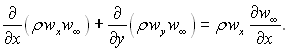
Віднімемо почленно з отриманого рівняння попередній вираз, матимемо

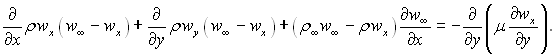(6.45)

Проінтегруємо тепер кожний член перетвореного рівняння руху (6.45) поперек пограничного шару:

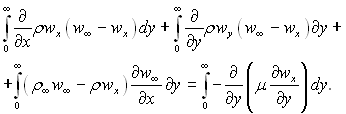
У цьому виразі 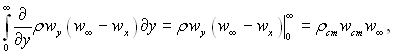тому що у випадку проникливої стінки при у = 0, w_x = 0, w_y = w_cm, ρ = ρ_cm; при y = ∞          w_x = w_∞, а

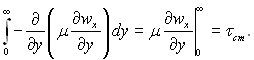
У цьому рівнянні τ_ст – напруга тертя на стінці.

Припускаючи існування інтегралів

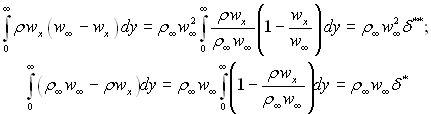
і припускаючи можливість заміни порядку диференціювання і інтегрування при нескінченній верхній межі, отримаємо

(6.46)

Виконуючи диференціювання рівняння (6.46) з урахуванням співвідношення (6.4)

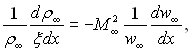(6.47)

отримаємо кінцевий вираз для інтегрального співвідношення імпульсів:

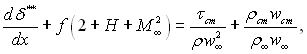(6.48)

де М_∞ = w_∞/a – число Маха, яке розраховується за параметром на зовнішній границі пограничного шару; швидкість звуку; Н = δ^*/δ^** – формфактор пограничного шару; 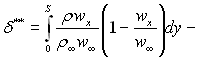товщина втрати імпульсу; 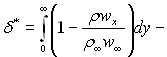товщина витіснення; 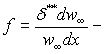формфактор, який характеризує аеродинамічну кривизну тіла, яке обтікається.

При обтіканні нестисливою рідиною (М << 1) рівняння (6.48) приймає вид

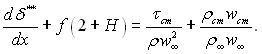(6.49)

Верхня межа інтегрування у виразах для товщини витіснення і товщини втрати імпульсу може бути замінена товщиною пограничного шару δ, при цьому суттєвих похибок до розрахунку не буде внесено. Величини δ^* і δ^** є важливими розрахунковими характеристиками пограничного шару.

Товщину витіснення, як слідує з рівності

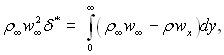
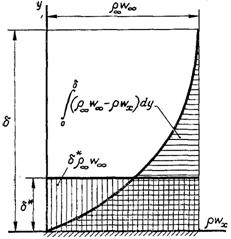
Рис.6.2. до визначення товщини витіснення

можна визначити (рис.6.2) як відрізок, через який секундні масові витрати ідеальної рідини дорівнював би втраті витрат в перерізі пограничного шару за рахунок гальмівної дії сил тертя під час руху реальної рідини. Як можна бачити з рисунка, товщина витіснення δ^* на відмінність від товщини пограничного шару δ – величина повністю визначена.

Перепишемо вираз для товщини втрати імпульсу δ^**

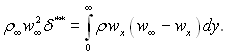
Можна за аналогією з товщиною витіснення визначити товщину втрати імпульсу δ^** як відрізок, через який при течії ідеальної рідини проходила б секундна кількість руху в перерізі пограничного шару за рахунок гальмівної дії сил тертя.

У випадку обтікання осесиметричних тіл обертання із-за малої товщини пограничного шару відносно радіуса кривизни R_x диференціальне рівняння руху залишається тим самим, що і при плоскій течії. Змінюється тільки форма рівняння суцільності потоку:

Це призводить до певної зміни інтегрального рівняння імпульсів, яке для випадку осесиметричної течії набуває наступного вигляду

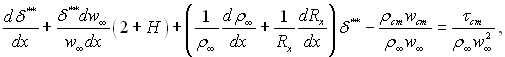(6.50)

де 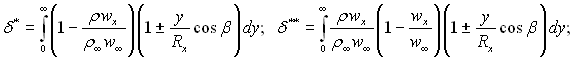R_x – радіус поперечного перерізу тіла; β – кут між дотичною до меридіану і віссю; х, у – осі координат, спрямовані: х – вздовж меридіального перерізу, у – перпендикулярно до профілю.

Інтегральне рівняння енергії виведемо аналогічним чином. Для цього диференціальне рівняння енергії, яке записане у формі (6.10), перетворимо за допомогою рівняння нерозривності потоку (6.2) до такого вигляду:

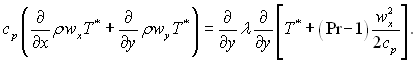
Помножимо обидві частини рівняння нерозривності потоку на значення ентальпії гальмування на зовнішній границі пограничного шару

яку в більшості випадків можна вважати постійною величиною:

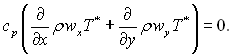
Віднімемо з кожного члена рівняння енергії попереднє співвідношення і проінтегруємо отриманий вираз поперек пограничного шару:

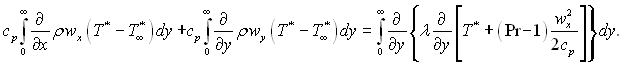
Використовуючи граничні умови при у = 0 w_y = w_cm, T^* = T_cm, ρ = ρ_cm і при у = ∞ w_y = 0, w_x = w_∞, T^* = T_∞^* , перетворимо інтеграли отриманого рівняння:

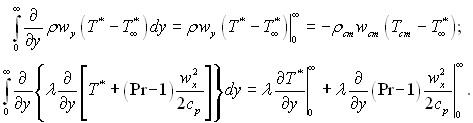
В останньому інтегралі 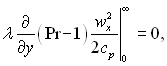тому що на стінці w_x = 0, а на зовнішній границі пограничного шару w_x = w_∞.

Введемо поняття товщини втрати енергії (ентальпії)

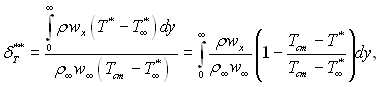(6.51)

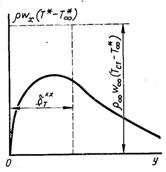
Рис.6.3. Графічна уява товщини втрати енергії

фізичний зміст якого пояснюється рис.6.3, перепишемо інтеграл в наступному виді

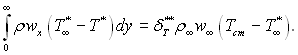
Так само, як і при виводі інтегрального рівняння імпульсів, вважаємо, що операції диференціювання і інтегрування можна поміняти місцями. Підставляючи значення інтегралів у вихідне рівняння, при цьому зауважимо, що 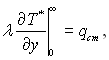отримаємо

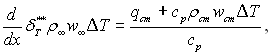(6.52)

де ΔТ = Т_ст – Т_∞^*.

Диференціюємо ліву частину отриманого рівняння, маючи на увазі, що всі величини, які стоять під знаком диференціалу, є функціями від х:

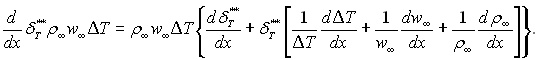
Введемо число подібності Стентора:

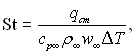
яке дозволяє перетворити інтегральний вираз енергії пограничного шару до кінцевого виду:

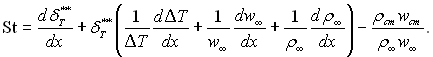(6.53)

Введемо число М_∞ згідно рівняння (6.47) у праву частину виразу (6.53), отримаємо

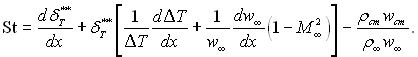(6.54)

Інколи, як у випадку реагуючих газів, бажано мати інтегральний вираз енергії, записаний через повну ентальпію гальмування h(₀. Виконуючи аналогічні перетворення і інтегруючи диференціальне рівняння енергії, записане через повну ентальпію (6.34) по у, отримаємо наступний інтегральний вираз:

де інтегральна товщина шару втрати енергії:

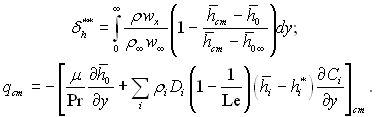
Введемо число подібності St, яке визначається співвідношенням

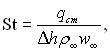(6.55)

и виконавши диференціювання по х, отримаємо кінцевий вираз

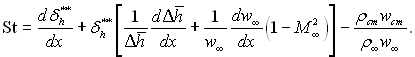(5.56)

У випадку обтікання осесиметричних тіл до інтегрального виразу додатково вводять, як і в рівняння імпульсів, радіус R_x:

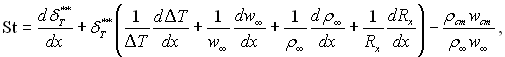(6.57)

де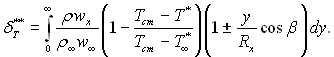

Інтегруючи рівняння дифузії і-го компонента (6.19) по перерізу пограничного шару і враховуючи рівняння нерозривності потоку, отримаємо інтегральне співвідношення речовини:

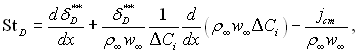(6.58)

де різниця масових часток дифундуючої речовини на стінці

і в потоці; 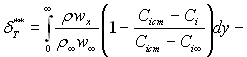товщина втрати дифундуючої речовини; 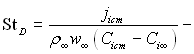дифузійне число Стентона.

Інтегральні співвідношення можна також отримати, розглядаючи баланс кількості руху, енергії і речовини для елементарного об’єму, виділеного двома перерізами в пограничному шарі, що свідчить про справедливість отриманих співвідношень як для ламінарного, так і для турбулентного режимів руху рідини в пограничному шарі.

В інтегральні співвідношення імпульсів енергії і речовини входять величини які представляють собою деякі фізичні масштаби пограничного шару. Зручність використання цих величин, як масштабів, криється в тому, що на відміну від товщини пограничного шару інтегральні товщини не зв’язані з уявленнями пограничного шару кінцевої товщини. При цьому структура рівнянь енергії (6.54, 6.56), речовини (6.58) і імпульсів (6.48) показують, що найбільш суттєві значення мають величини Виходячи з цього зручно записати характерні числа Re динамічного, теплового і дифузійного пограничних шарів у наступному виді:

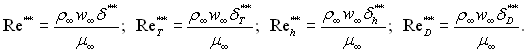
Введемо в інтегральні вирази (6.49), (6.53) і (6.58), складені для випадку обтікання поверхні плоским нестисливим потоком, замість товщини втрати імпульсу, енергії і речовини відповідні числа Re. Після нескладних перетворень отримаємо:

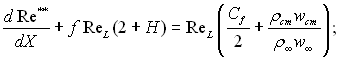(6.59)

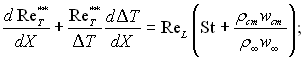(6.60)

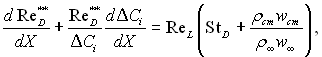(6.61)

де Re_L – число Рейнольдса, побудоване по характерному розміру L поверхні, що обтікає; Х = х/L – відносна відстань; С_f = 2t_cm/(r_Ґw^2Ґ) – коефіцієнт тертя.

Інтегральні рівняння імпульсів, енергії і речовини для стислого потоку газу, який хімічно реагує, зберігають вид рівнянь (6.59)...(6.61), якщо прийняти:

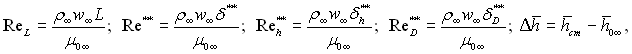
де m_0Ґ – значення динамічної в’язкості, розраховане за параметрами гальмування спокійного потоку (див. рис.6.1).

В окремому випадку з рівняння енергії (6.56) можна отримати інтегральне співвідношення енергії для газу, який хімічно реагує, яке співпадає з (6.60):

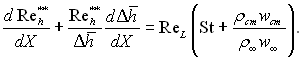
Отримані інтегральні рівняння можна розв’язати, якщо відомі закони опору, теплообміну і масообміну, які в загальному випадку можна представити так:

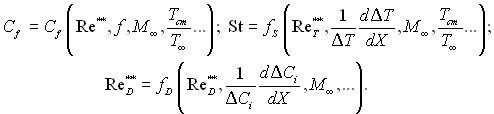
Вигляд цих функцій залежить від режиму течії рідини в пограничному шарі. Пізніше покажемо, що для ламінарної течії закони тертя, теплообміну і масообміну можна отримати при певних граничних умовах аналітичним шляхом. Для турбулентного режиму течії закони тертя, теплообміну і масообміну отримують на підставі напівемпіричної теорії турбулентності із залученням дослідних даних.

Також покажемо, що закони тертя, теплообміну і масообміну консервативні до зміни граничних умов. Отримані для стандартних умов, тобто для без градієнтного обтікання пластини нестиглим потоком з постійною температурою і концентрацією речовини на стінці, вони можуть бути використані і для більш складних умов.

Усе розмаїття граничних умов досить повно враховується при інтегруванні рівнянь імпульсів, енергії і дифузії.

Введемо до правих частин інтегральних рівнянь (6.59)...(6.61) значення коефіцієнта тертя С_f0, теплового St₀ і дифузійного St_D0 чисел Стентона, отриманих для стандартних умов і одних і тих же чисел Re^**, побудованих за відповідними товщина ми:

(6.62)

(6.63)

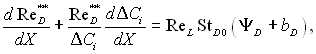(6.64)

де 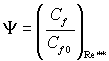– відносний закон тертя при ; 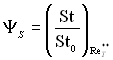– відносний закон теплообміну при 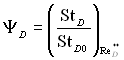– відносний закон дифузії при 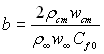– параметр проникливості стінки віднесений до С_f0; 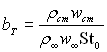– тепловий параметр проникливості, віднесений до St₀; 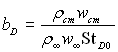– дифузійний параметр проникливості, віднесений до St_D0.