




–озд≥л 12. “≈ѕЋќќЅћ≤Ќ ѕ–» ќЌƒ≈Ќ—ј÷≤ѓ ѕј–» « ѕј–ќ-√ј«ќ¬ќѓ —”ћ≤Ў≤
12.1. ќдном≥рн≥ задач≥ дифуз≥њ
«адача про теплообм≥н п≥д час конденсац≥њ з паро-газовоњ сум≥ш≥ у повн≥й постановц≥ повинна розгл€датис€ €к спр€жена задача. –езультуючий коеф≥ц≥Їнт теплов≥ддач≥ залежить в≥д двох терм≥чних опор≥в Ц дифуз≥йного опору ≥ опору конденсату. ÷≥ два терм≥чних опори взаЇмозвТ€зан≥, що у загальному випадку не дозвол€Ї попередньо задати розпод≥л густини потоку маси ≥ пари, що конденсуЇтьс€, на поверхн≥ фазового переходу. «нанн€ розпод≥лу ц≥Їњ величини необх≥дне дл€ розвТ€зку дифуз≥йноњ частини задач≥.
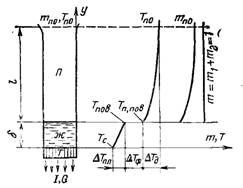
–ис.12.1. ƒо наближеного методу розвТ€зку спр€женоњ задач≥
–озгл€немо стац≥онарний одном≥рний ≥зотерм≥чний процес дифуз≥њ пари зг≥дно схеми рис.12.1. –озвТ€зок под≥бних задач ≥нколи корисний при вивченн≥ конденсац≥њ пари з паро-газовоњ сум≥ш≥.
ƒиференц≥альне р≥вн€нн€ масообм≥ну (9.18) у розгл€дуваному випадку суттЇво спрощуЇтьс€:
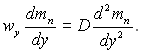 (12.1)
(12.1)
√раничн≥ умови: ![]()
” р≥вн€нн≥ (12.1) л≥вий член враховуЇ стефан≥в пот≥к, €кий неминуче зТ€вл€Їтьс€ дл€ ≥нертного компоненту (газу). √устина потоку пари ≥ газу на м≥ж фазн≥й границ≥:
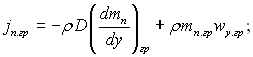 (12.2)
(12.2)
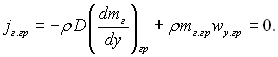 (12.3)
(12.3)
« р≥вн€нь (12.2) ≥ (12.3) виходить, що швидк≥сть стефанового потоку може визначатис€ сп≥вв≥дношенн€м:
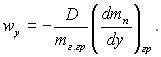 (12.4)
(12.4)
ѕ≥дставл€ючи значенн€ wy в р≥вн€нн€ (12.1) ≥ позначаючи η = тп Ц 1, отримаЇмо наступне диференц≥альне р≥вн€нн€:
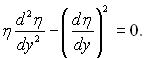 (12.5)
(12.5)
–озвТ€зок цього р≥вн€нн€ буде таким:
![]() (12.6)
(12.6)
де зг≥дно до граничних умов
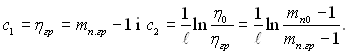
–озпод≥л в≥дносних концентрац≥й можна описати тод≥ сп≥вв≥дношенн€м
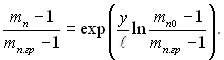 (12.7)
(12.7)
« (12.6) виходить, що
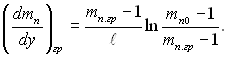
“од≥ з р≥вн€нь (12.2) ≥ (12.4) можна отримати наступний вираз дл€ густини потоку пари на поверхн≥ фазового переходу:
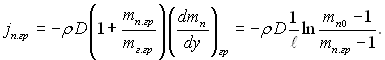 (12.8)
(12.8)
ѕри запису останнього р≥вн€нн€ враховано, що тг+ тп = 1 при дов≥льному значенн≥ у. ¬ираз (12.8) визначаЇ густину потоку маси не т≥льки на м≥ж фазн≥й поверхн≥, але ≥ при ус≥х значенн€х у в≥д 0 до ℓ.
« р≥вн€нн€ (12.8) ≥ р≥вн€нн€ масов≥ддач≥
![]() (12.9)
(12.9)
отримуЇмо наступний вираз дл€ коеф≥ц≥Їнта масов≥ддач≥:
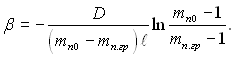 (12.10)
(12.10)
ƒифуз≥йне число Ќуссельта тод≥ визначаЇтьс€ сп≥вв≥дношенн€м:
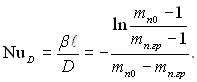 (12.11)
(12.11)
ѕриведемо р≥шенн€ дл€ випадку одном≥рноњ дифуз≥њ до безмежного цил≥ндра.![]() ƒиференц≥альне р≥вн€нн€ одном≥рноњ стац≥онарноњ ≥зотерм≥чноњ дифуз≥њ з урахуванн€м переносу в цил≥ндричних координатах запишетьс€ наступним чином:
ƒиференц≥альне р≥вн€нн€ одном≥рноњ стац≥онарноњ ≥зотерм≥чноњ дифуз≥њ з урахуванн€м переносу в цил≥ндричних координатах запишетьс€ наступним чином:
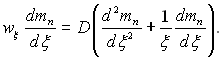 (12.12)
(12.12)
√раничн≥ умови:
при ξ = Rm (на поверхн≥ цил≥ндра) тп = тп.гр.; при ξ = Rℓ тп = тп0
ƒл€ даноњ постановки задач≥ л≥н≥йна густина потоку пари jℓn, кг/(мЈс),не залежить в≥д рад≥уса о у зв'€зку з д≥Їю закону збереженн€ маси. як ≥ ран≥ше вважаЇмо, що м≥ж фазна поверхн€ непрониклива дл€ газу.
ѕри η2 ≠ 0 ≥нтегруванн€ р≥вн€нн€ (12.12) даЇ:
![]() (12.13)
(12.13)
¬изначивши з граничних умов стал≥ ≥нтегруванн€, можна отримати наступн≥ вирази, €к≥ характеризують масообм≥н. √устина потоку пари га границ≥ розд≥лу фаз ξ= Rm виражаЇтьс€ залежн≥стю
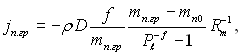 (12.14)
(12.14)
де 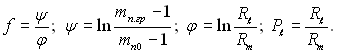
ƒифуз≥йне число Ќуссельта:
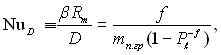 (12.15)
(12.15)
де коеф≥ц≥Їнт масообм≥ну в в≥днесений до р≥зниц≥ паровм≥ст≥в тп0 Ц тп.гр.
–≥вн€нн€ (12.15) п≥сл€ певних перетворень можна записати через безрозм≥рн≥ параметри πD ≥ εг0, запропонованих Ћ.ƒ.Ѕерманом:
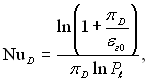 (12.16)
(12.16)
де πD = (рп0 Ц рп.гр)/р; εг0 = рг.0/р; рп0, рп.гр. Ц парц≥альн≥ тиски пари в≥дпов≥дно при ξ=Rℓ ≥ ξ = Rm; рг.0 Ц парц≥альний тиск газу при ξ=Rℓ; р Ц повний тиск сум≥ш≥.
ћодель процесу, €ку покладено в основу розгл€нутих задач, виключаЇ сили вТ€зкост≥: у напр€мку, поперечному дифуз≥йн≥й мас≥, швидк≥сть ≥ температура не зм≥нюютьс€, ф≥зичн≥ параметри пост≥йн≥. ” насл≥док цього з перел≥ку актуальних безрозм≥рних випадають числа –ейнольдса, ѕрандтл€ ≥ јрх≥меда.
ѕри невисок≥й ≥нтенсивност≥ дифуз≥њ процес переносу можна вважати локально р≥вноважним. ѕара вважаЇтьс€ насиченою, ≥ кожному значенню њњ концентрац≥њ в≥дпов≥даЇ певне значенн€ температури насиченн€. “аким чином, полю концентрац≥й в≥дпов≥даЇ поле температур ≥ умова ≥зотерм≥чност≥ процесу виконуЇтьс€, строго кажучи, т≥льки у граничному випадку малих зм≥н концентрац≥й.
«м≥на концентрац≥й ≥ температури в обТЇм≥ парогазовоњ сум≥ш≥ призводить до зм≥ни њњ густини, внасл≥док чого може виникнути в≥льний рух. ѕор≥вн€нн€ р≥шенн€ (12.15) з досл≥дними даними, отриманими в умовах близьких до умов теоретичноњ задач≥, показуЇ, що припущенн€ про ≥зотерм≥чн≥сть процесу ≥ пост≥йност≥ густини сум≥ш≥ виправдовуютьс€ при
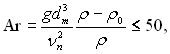
де ρ ≥ ρ0 Ц в≥дпов≥дно густини сум≥ш≥, €к≥ в≥дпов≥дають Rℓ ≥ Rm. якщо Ar ≥ 50, то
![]() (12.17)
(12.17)
де NuD0 Ц дифуз≥йне число Ќуссельта, €ке розраховуЇтьс€ по формул≥ (12.15).
—п≥вв≥дношенн€ (12.8), (12.11), (12.14) ≥ (12.15) можуть бути основою дл€ побудови в≥дпов≥дних розрахункових формул ≥ анал≥зу досл≥дних даних.
12.2. онденсац≥€ на вертикальн≥й ст≥нц≥
–озгл€немо конденсац≥ю пари з паро-газового потоку сум≥ш≥, що рухаЇтьс€ зверху вниз по вертикальн≥й плоск≥й ст≥нц≥ незм≥нн≥й температур≥ “с (рис.12.1). ѕара вважаЇтьс€ насиченою (задовольн€Їтьс€ локальна терм≥чна р≥вновага). «адан≥ швидк≥сть, температура ≥ концентрац≥€ газу у спок≥йному потоц≥ w0, T0, mг0. «наченн€ цих величин на поверхн≥ р≥дкоњ пл≥вки wгр, Tгр, mг.гр. зав≥дому нев≥дом≥ ≥ п≥дл€гають визначенню. —формульована таким чином задача Ї спр€женою. Ќаведемо њњ математичне формулюванн€ в наближен≥ пограничного шару.
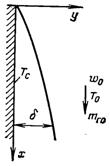
–ис.12.2. ƒо постановки задач≥ про конденсац≥ю пари з паро-газовоњ сум≥ш≥
ѕаро-газова сум≥ш:
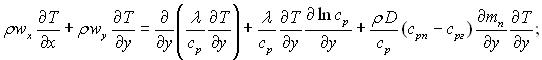 (12.18)
(12.18)
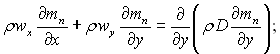 (12.19)
(12.19)
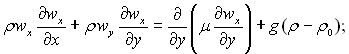 (12.20)
(12.20)
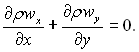 (12.21)
(12.21)
¬важаЇтьс€, що швидк≥сть паро-газовоњ сум≥ш≥ не дуже велика, тому випущен≥ члени, €к≥ враховують дисипац≥ю механ≥чноњ енерг≥њ ≥ стислив≥сть. ”раховуЇтьс€ концентрац≥йна дифуз≥€, ≥ншими видами дифуз≥њ нехтуЇмо. ‘≥зичн≥ параметри паро-газовоњ сум≥ш≥ ≥ндексами не позначаютьс€.
ƒл€ р≥дкоњ фази систему р≥вн€нь запишемо у наближенн≥ Ќуссельта:
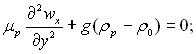 (12.22)
(12.22)
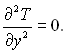 (12.23)
(12.23)
√раничн≥ умови:
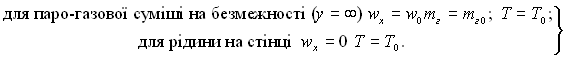 (12.24)
(12.24)
”мови спр€женн€ (у = δ):
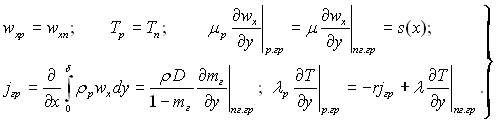 (12.25)
(12.25)
ќкр≥м цього, вважаЇтьс€ можливим використанн€ р≥вн€нн€ стану дл€ сум≥ш≥:
р = ρRT. (12.26)
—истему р≥вн€нь замикаЇ р≥вн€нн€ балансу тепла, складене дл€ р≥дкоњ пл≥вки, €ке визначаЇ њњ товщину:
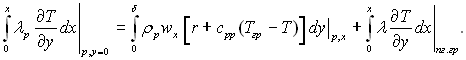 (12.27)
(12.27)
” цьому р≥вн€нн≥ враховуЇтьс€ кр≥м теплоти фазового переходу переохолодженн€ конденсату ≥ конвективна теплов≥ддача в≥д паро-газовоњ сум≥ш≥ до пл≥вки р≥дини.
«аписана система р≥вн€нь не зводитьс€ до системи звичайних диференц≥альних р≥вн€нь. Ќа сьогодн≥шн≥й день њњ розвТ€зок можливий т≥льки числовими методами.
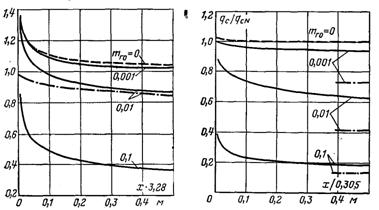
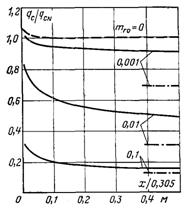
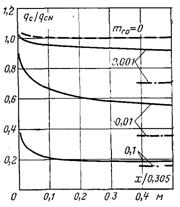
“ак≥ розрахунки виконан≥ дл€ випадку конденсац≥њ вод€ноњ пари з паро-газовоњ сум≥ш≥. ’арактерн≥ параметри мали наступн≥ значенн€: “0 = 383, 338,5 ≥ 311 ; “0 Ц “с = 2,8, 11 ≥ 22,2 ; w0 = 0,03, 0,3 ≥ 3 м/с; тг0 = 0, 0,001 ≥ 0,1. –езультати розрахунку навод€тьс€ у вигл€д≥ залежност≥ в≥дносного теплового потоку qc/qc.N в≥д х, тг0, w0, “0 ≥ (“0 Ц “с) [де qc.N Ц густина теплового потоку на ст≥нц≥, €ка визначаЇтьс€ за класичною теор≥Їю Ќуссельта дл€ температурного напору (“0 Ц “с), вважаючи що в≥дсутнЇ терт€ пари, а зм≥нн≥ ф≥зичн≥ параметри р≥дини розраховувалис€ за визначальною температурою “визн = “0 + 0,33(“0 Ц Ц “с)]. ƒе€к≥ результати розрахунк≥в наведено на рис.12.3а...г. ѕри анал≥з≥ граф≥к≥в необх≥дно мати на уваз≥, що характер зменшенн€ теплов≥ддач≥ при зб≥льшенн≥ х обумовлений не т≥льки потовщенн€м пл≥вки, що маЇ м≥сце при конденсац≥њ чистоњ нерухомоњ пари.
а) б) в)
 г)
г)
–ис.12.3. “еплообм≥н при конденсац≥њ пари з паро-газовоњ сум≥ш≥ (суц≥льн≥ крив≥ побудован≥ дл€ трьох значень масовоњ концентрац≥њ пов≥тр€: тг =0,001, 0,01, 0,1; штрих крапка Ц в≥дсутнЇ терт€, w0 = 0; штрихова крива Ц чиста пара, тг0 = 0): а Ц w0 = 3 м/c, “0 = 373 , Δ“ = 22,2 ;
б Ц w0 = 0,3 м/c, “0 = 373 , Δ“ = 2,8 ; в Ц w0 = 0,3 м/c,
“0 = 373 , Δ“ = 11 ; г Ц w0 = 0,3 м/c, “0 = 373 , Δ“ =
22,2
Ќа рисунках наводитьс€ результуючий ефект, обумовлений також впливом швидкост≥ сум≥ш≥ на дифуз≥йний терм≥чний оп≥р ≥ на величину терт€ на поверхн≥ пл≥вки. ∆аль, що в≥дсутн≥ узагальнююч≥ розрахунков≥ залежност≥, що затрудн€Ї анал≥з отриманого матер≥алу ≥ його практичне використанн€. «робимо певн≥ висновки €к≥сного характеру.
–озвиток пограничного шару в сум≥ш≥ визначаЇтьс€ двома основними обставинами Ц сильним в≥дсмоктуванн€м на поверхн≥ фазових перетворень ≥ зм≥нною конвекц≥Їю. ƒл€ останньоњ маЇ значенн€ сп≥вв≥дношенн€ швидкостей w0 ≥ wгр, а також в≥льна конвекц≥€, €ка виникаЇ внасл≥док зм≥ни густини поперек пограничного шару.
якщо в≥дносна швидк≥сть (w0 Ц wгр) велика ≥ jгр → 0, то дифуз≥йне число Ќуссельта наближаЇтьс€ до значенн€, €ке визначаЇтьс€ формулою
![]()
де Renx = w0x/ν; PrD = ν/D.
ѕри заданих “0, (“0 Ц “с) ≥ тг0 в≥дношенн€ qc/qc.N зб≥льшуЇтьс€ з ростом w0 ≥ зменшуЇтьс€ з≥ зб≥льшенн€м х (див. рис.12.3). ѕри невеликих значенн€х w0 ц≥ ефекти менш виражен≥, особливо при висок≥й концентрац≥њ газу, внасл≥док зм≥ни характеру конвекц≥њ в паровому пограничному шар≥ (перех≥д в≥д вимушеного до в≥льного руху). ¬плив температури “0 про€вл€Їтьс€ через густину сум≥ш≥.
—кладн≥сть задач конвективного масообм≥ну примушуЇ шукати наближен≥ ≥ б≥льш прост≥ методи розрахунк≥в.
12.3. јналог≥€ процес≥в теплообм≥ну ≥ масообм≥ну
«апишемо математичн≥ формулюванн€ задач про окремо прот≥каючи стац≥онарних процесах теплообм≥ну ≥ масообм≥ну при повздовжньому омиванн≥ плоскоњ поверхн≥. ‘ормулюванн€ наведемо у наближенн≥ пограничного шару, вважаючи теч≥ю без град≥Їнтною, ф≥зичн≥ параметри пост≥йн≥ ≥ швидкост≥ пом≥рн≥.
ƒл€ теплообм≥ну запишемо р≥вн€нн€ енерг≥њ, руху ≥ нерозривност≥ потоку, призначивши найпрост≥ш≥ граничн≥ умови:
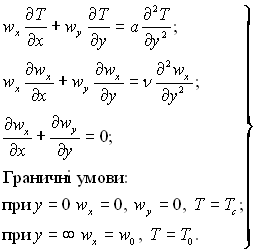 (12.28)
(12.28)
ƒифуз≥йний процес у формулюванн≥ задач≥ не врахований, що дл€ не≥зотерм≥чного середовища строго виконуЇтьс€, €кщо середовище Ї однокомпонентним.
ƒл€ масообм≥ну сформулюЇмо задачу, вважаючи середовище двохкомпонентним (≥ = 1, 2) ≥ ст≥нку проникливою дл€ одного з компонент≥в (наприклад дл€ першого). “еч≥ю вважаЇмо ≥зотерм≥чною. ¬ ≥ншому умови не в≥др≥зн€ютьс€ в≥д ран≥ше наведених умов дл€ теплообм≥ну. “од≥ маЇмо:
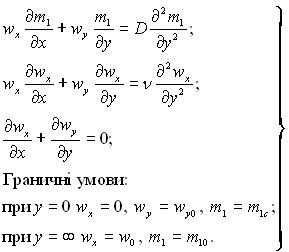 (12.29)
(12.29)
ѕор≥внюючи математичн≥ формулюванн€ (12.28) ≥ (12.29), можна сказати, що вони ≥дентичн≥ у всьому, кр≥м завданн€ умови дл€ нормальноњ компоненти швидкост≥ при у = 0. ƒл€ тепловоњ задач≥ ≥з-за непроникливост≥ ст≥нки задано wy(x, 0) = 0. ƒл€ дифуз≥йноњ wy(x, 0) = wy0, де у загальному випадку швидк≥сть поперечного потоку wy0 може бути функц≥Їю х. якщо покласти що wy0 → 0, то у першому наближенн≥ вважати, що р≥шенн€ задач (12.28) ≥ (12.29) будуть ≥дентичними. « формальноњ точки зору однаково, €ку з цих задач розвТ€зувати, €кщо wy0 → 0. ѕол€ температур ≥ концентрац≥й будуть в≥др≥зн€тис€ на сталу величину чи повн≥стю сп≥впадати при безрозм≥рному поданн≥ D ≥ α. ” ц≥й ≥дентичност≥ ≥ пол€гаЇ аналог≥€ (чи под≥бн≥сть) процес≥в теплообм≥ну ≥ масообм≥ну.
–озгл€даючи аналог≥ю процес≥в теплообм≥ну ≥ масообм≥ну, розр≥зн€ють окрем≥ ≥ сум≥сн≥ процеси, €к≥ в≥дбуваютьс€ перенос≥ теплоти ≥ маси. “еплообм≥н ≥ масообм≥н при сум≥сному прот≥канн≥ Ї б≥льш складним ≥ тому трудн≥ше п≥ддаЇтьс€ вивченню ≥ менш досл≥джений процес, н≥ж теплообм≥н, не ускладнений масообм≥ном. ѕрактичну ц≥нн≥сть представл€Ї можлив≥сть використанн€ накопиченого в теор≥њ теплообм≥ну великоњ ≥нформац≥њ про процеси в однофазному середовищ≥ з непроникливою фазовою границею дл€ розрахунку процес≥в, €к≥ ускладнен≥ супутн≥м масообм≥ном.
ѕри конденсац≥њ м≥жфазна границ€ прониклива хоч би дл€ одного з компонент≥в ¬иникаЇ поперечний пот≥к маси, тобто нормальна складова швидкост≥ на поверхн≥ розриву стаЇ в≥дм≥нною в≥д нул€. ѕо€ва поперечного потоку зм≥нюЇ розпод≥л швидкост≥, концентрац≥й ≥ температури у сум≥ш≥, що в≥дбиваЇтьс€ на ≥нтенсивност≥ переносу теплоти ≥ маси.
ћожна вважати, що малий поперечний пот≥к речовини не буде суттЇво впливати на теч≥ю ≥ теплообм≥н. ’арактеристики повздовжнього омиванн€ т≥ла при цьому практично не зм≥нюютьс€. ѕри досить великому поперечному потоц≥ останн≥й може перевищувати повздовжн≥й. ѕроцес при цьому €к≥сно зм≥нюЇтьс€. —лабка повздовжн€ теч≥€ вздовж поверхн≥ теплообм≥ну може подавл€тис€ поперечною ≥ на к≥нець не впливати на характеристики переносу. якщо вздовж фазовоњ поверхн≥ умови не зм≥нюютьс€, процес може в≥дпов≥дати розгл€нутому ран≥ше в одном≥рн≥й задач≥ (І 12.1).
ѕ≥дх≥д до вир≥шенн€ двох в≥дм≥чених задач р≥зний. “ому необх≥дно установити границ≥ переходу. ѕри цьому область ≥снуванн€ аналог≥њ теплообм≥ну ≥ масообм≥ну вважаЇтьс€ область несуттЇвого впливу поперечного потоку на теплоперенос. ¬и€вленню меж ≥снуванн€ аналог≥њ присв€чено р€д досл≥джень, в €ких використан≥ теоретичн≥ ≥ експериментальн≥ результати, отриман≥ дл€ вимушеноњ ≥ в≥льноњ конвекц≥њ при р≥зних умовах омиванн€ ≥ дл€ р≥зних сум≥ш≥в. –езультати р≥шень ≥ експеримент≥в представлен≥ у вид≥ наступних залежностей дл€ масо - ≥ теплообм≥ну:
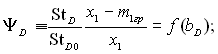 (12.30)
(12.30)
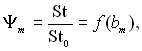 (12.31)
(12.31)
де 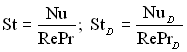 Ц числа —тентора в≥дпов≥дно дл€ сум≥сного проходженн€ процес≥в теплов≥ддач≥ ≥ масов≥ддач≥; St0 ≥ StD0 Ц т≥ ж числа при в≥дсутност≥ впливу поперечного потоку маси на теч≥ю; х ≥ т Ц в≥дносн≥ масов≥ концентрац≥њ компонента в конденсат≥ ≥ в сум≥ш≥; ≥ндекс У1Ф стосуЇтьс€ активного (високо кипл€чого) компоненту сум≥ш≥ (пара, €кщо розгл€даЇтьс€ перо-газова сум≥ш); ≥ндекс УгрФ≥
∞ Ц в≥дпов≥дно на границ≥ розд≥лу фаз ≥ на в≥ддал≥ в≥д нењ.
Ц числа —тентора в≥дпов≥дно дл€ сум≥сного проходженн€ процес≥в теплов≥ддач≥ ≥ масов≥ддач≥; St0 ≥ StD0 Ц т≥ ж числа при в≥дсутност≥ впливу поперечного потоку маси на теч≥ю; х ≥ т Ц в≥дносн≥ масов≥ концентрац≥њ компонента в конденсат≥ ≥ в сум≥ш≥; ≥ндекс У1Ф стосуЇтьс€ активного (високо кипл€чого) компоненту сум≥ш≥ (пара, €кщо розгл€даЇтьс€ перо-газова сум≥ш); ≥ндекс УгрФ≥
∞ Ц в≥дпов≥дно на границ≥ розд≥лу фаз ≥ на в≥ддал≥ в≥д нењ.
‘актори проникливост≥ 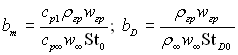 представл€ють собою в≥дносн≥ поперечн≥ потоки маси. «наченню b
в≥дпов≥даЇ в≥дсутн≥сть поперечного потоку
(jгр
= ρгрwгр = 0). ѕри b → ∞ дом≥нуЇ поперечний пот≥к.
представл€ють собою в≥дносн≥ поперечн≥ потоки маси. «наченню b
в≥дпов≥даЇ в≥дсутн≥сть поперечного потоку
(jгр
= ρгрwгр = 0). ѕри b → ∞ дом≥нуЇ поперечний пот≥к.
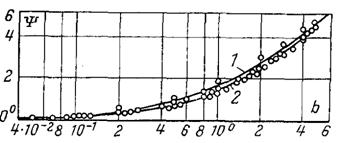
↑–ис.12.4. ¬плив поперечного потоку маси на теплов≥ддачу ≥ масов≥ддачу Ц сп≥вставленн€ теоретичних р≥шень: 1 Ц лам≥нарний пограничний шар; 2 Ц турбулентний пограничний шар
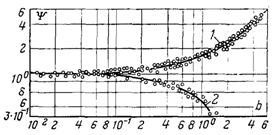
–ис.12.5. ¬плив поперечного потоку маси на теплов≥ддачу ≥ масов≥ддачу Ц сп≥вставленн€ досл≥дних даних: 1 Ц конденсац≥€ (в≥дсмоктуванн€); 2 Ц випаровуванн€ (вдув) ↑
на рис. 12.4 ≥ 12.5 наведен≥ теоретичн≥ ≥ досл≥дн≥ дан≥, опрацьован≥ у вигл€д≥ залежностей (12.30), (12.31). Ќа рис.12.4 представлен≥ теоретичн≥ досл≥дженн€ теплообм≥ну ≥ масообм≥ну: дл€ лам≥нарного ≥ турбулентного пограничних шар≥в на пластин≥; дл€ лобовоњ тв≥рноњ цил≥ндра; при сум≥сн≥й д≥њ в≥льноњ ≥ вимушеноњ конвекц≥њ у випадку лам≥нарного обт≥канн€ пластини; дл€ ком≥рчастоњ конвекц≥њ; дл€ турбулентноњ теч≥њ у труб≥; дл€ в≥льноњ конвекц≥њ б≥л€ вертикальноњ пластини. –≥шенн€ отриман≥ €к дл€ однокомпонентного середовища з в≥дсмоктуванн€м, так ≥ дл€ двокомпонентних середовищ.
Ќа рис.12.5 наведен≥ результати експериментальних досл≥джень теплообм≥ну ≥ масообм≥ну при конденсац≥њ вод€ноњ пари з двокомпонентних сум≥ш≥в з гел≥Їм, пов≥тр€м ≥ фреоном-12, дл€ сум≥ш≥в пар≥в (етанол Ц вода, етанол Ц пропаном, етанол Ц бутанол), а також дан≥ з пористого в≥дсмоктуванн€ ≥ вдуванн≥. ” досл≥дах мало м≥сце поперечне омиванн€ цил≥ндра, в≥льна конвекц≥€ б≥л€ пластини, у к≥льцевому зазор≥ ≥ б≥л€ горизонтального цил≥ндра. ƒодатна залежн≥сть Ψ(b) в≥дпов≥даЇ конденсац≥њ (в≥дсмоктуванню), в≥дТЇмна Ц випарюванню (вдуванню). ѕри bD(m) ≤ 0,1 крив≥ дл€ конденсац≥њ ≥ випаровуванн€ сп≥впадають.
«алежност≥, наведен≥ на рис.12.4 ≥ 12.5, дозвол€ють з достатн≥м наближенн€м ви€вити область достов≥рност≥ аналог≥њ м≥ж розд≥льно прот≥каючи ми процесами тепло- ≥ масообм≥ну. јналог≥њ в≥дпов≥даЇ умова bD(m) ≤ 0,1. ѕри bD(m) ≥ 4 4 в≥дбуваЇтьс€ виродженн€ чисел –ейнольдса ≥ ѕрандтл€ на процеси переносу ≥ знаходить м≥сце граничний випадок переважанн€ поперечного потоку.
12.4. “епломасообм≥н при конденсац≥њ в елементах теплообм≥нних пристроњв
« причини складност≥ процес≥в конденсац≥њ з паро-газовоњ сум≥ш≥ в ≥нженерних розрахунках отриман≥ досл≥дним шл€хом дан≥. Ќаведемо де€к≥ результати експериментальних досл≥джень масов≥ддач≥ при найб≥льш актуальних в енергетиц≥ елемент≥в теплообм≥нних пристроњв. “еплообм≥н при конденсац≥њ вод€ноњ пари у турбулентному потоц≥ паро-газовоњ сум≥ш≥ зд≥йснювавс€ в порист≥й труб≥ д≥аметром 10 мм ≥ довжиною 175 мм р≥вном≥рно покрит≥й р≥диною, терм≥чний оп≥р €коњ малий ≥з-за в≥дсмоктуванн€ конденсату через пористу ст≥нку.
” досл≥дах використовувалас€ сум≥ш вод€ноњ пари з гел≥Їм, пов≥тр€м ≥ фреоном 12. “иск паро-газовоњ сум≥ш≥ складав р = 0,1...0,13 ћѕа; початковий вм≥ст газу в сум≥ш≥ εг = рг/р = 0,1...1,0; безрозм≥рна р≥зниц€ парц≥альних тиск≥в πD = 0,02...0,4; швидк≥сть паро-газовоњ сум≥ш≥ була w = 2...25 м/с; число –ейнодьдса зм≥нювалос€ в д≥апазон≥ Re = (2...25)Ј103
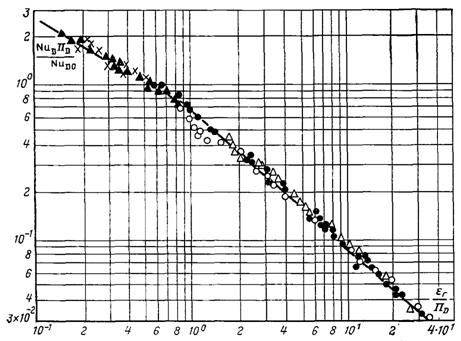
–ис.12.6. ћасов≥ддача при конденсац≥њ пари з паро-газовоњ сум≥ш≥ в труб≥: Ш Ц вод€на пара Ц пов≥тр€; p Ц вод€на пара Ц гел≥й; Щ Ц вод€на пара Ц фреон-12; r Ц вод€на пара Ц пов≥тр€; ќ Ц кал≥й Ц аргон
ƒосл≥дн≥ дан≥ опрацьован≥ у вигл€д≥ залежност≥ м≥ж числами под≥б-ност≥ запропонова-ними Ћ.ƒ.Ѕерманом. –езультати опрацюванн€ досл≥дних даних наведен≥ на рис.12.6 у вигл€д≥ залежност≥:
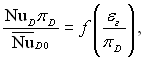
де ![]() Ц дифуз≥йне число Ќуссельта, розраховане на основ≥ наближеноњ аналог≥њ розд≥льного прот≥канн€ процес≥в теплообм≥ну ≥ масообм≥ну,
Ц дифуз≥йне число Ќуссельта, розраховане на основ≥ наближеноњ аналог≥њ розд≥льного прот≥канн€ процес≥в теплообм≥ну ≥ масообм≥ну,
![]()
ƒосл≥дн≥ дан≥ наведен≥ на рис.12.6 апроксимуютьс€ залежн≥стю:
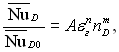 (12.32)
(12.32)
де ј = 0,71; п = Ц0,6; т = Ц0,4 (при 10Ц1≤ εг/πD≤1,0); ј = 0,71; п = Ц0,9; т = Ц0,1 (при εг/πD >1,0). ¬ област≥ εг/πD = (1...3) дос€гаЇтьс€ краще сходженн€ досл≥дних даних, €кщо до правоњ частини формули (12.32) добавити сп≥вмножник (Rn/Rг)Ц0,1, де Rn ≥ Rг Ц в≥дпов≥дно газов≥ стал≥ пари ≥ газу. ѕри цьому ј = 0,745.
Ќе менш практично важливою Ї задача про теплообм≥н при пл≥вков≥й конденсац≥њ пари, €ка рухаЇтьс€ в паро-газов≥й сум≥ш≥ на одиничних трубах ≥ трубних пучках. ѕ≥д час досл≥д≥в паропов≥тр€на сум≥ш надходила до одиничноњ горизонтальноњ труби зверху. “иск сум≥ш≥ зм≥нювавс€ в≥д 0,0046 до 0,089 ћѕа; вм≥ст пов≥тр€ у вод€н≥й пар≥ складав εг0 = 0,01...0,56. ƒл€ середнього коеф≥ц≥Їнта масов≥ддач≥ запропоноване р≥вн€нн€:
![]() (12.33)
(12.33)
€ке справедливе при Re = 350...4800. ” формул≥ (12.33) число –ейнольдса складене за швидк≥стю наб≥гаючого на трубу потоку сум≥ш≥ ≥ зовн≥шнього д≥аметра труби. ‘≥зичн≥ параметри сум≥ш≥ приймаютьс€ за параметрами наб≥гаючого потоку. оеф≥ц≥Їнт вТ€зкост≥ розраховуЇтьс€ по р≥вн€нню:
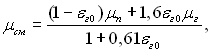
де μп ≥ μг Ц в≥дпов≥дно динам≥чний коеф≥ц≥Їнт вТ€зкост≥ пари ≥ пов≥тр€.
ƒосл≥ди по масообм≥ну при обт≥канн≥ пучк≥в труб, основн≥ параметри €ких наведено в І 11.6, проведен≥ дл€ низх≥дного потоку паропов≥тр€ноњ сум≥ш≥. ѕри цьому отримана наступна формула дл€ середнього коеф≥ц≥Їнта масов≥ддач≥ при Re = 350...4800:
![]() (12.34)
(12.34)
де, €к ≥ у формул≥ (12.33), 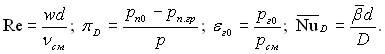
„исло –ейнольдса розраховуЇтьс€ за швидк≥стю паропов≥тр€ноњ сум≥ш≥ перед р€дом труб; визначальним розм≥ром Ї зовн≥шн≥й д≥аметр труб; параметри сум≥ш≥ визначаютьс€ так само, €к ≥ дл€ формули (12.33).
ћножник а у формул≥ (12.34) залежить в≥д номера р€ду: дл€ першого а = 0,53; дл€ другого а = 0,74; дл€ третього ≥ наступних а = 0,82. «м≥на коеф≥ц≥Їнта пропорц≥ональност≥ а по р€дам св≥дчить про подразненн€ паропов≥тр€ного потоку при його проходженн≥ через пучок, що приводить до зб≥льшенн€ коеф≥ц≥Їнта масов≥ддач≥. ” ц≥й обставин≥ можна вбачати певну аналог≥ю з теплов≥ддачею пучк≥в труб, €к≥ омиваютьс€ однокомпонентним середовищем.
–€дом автор≥в виконано експериментальне досл≥дженн€ теплообм≥ну при конденсац≥њ техн≥чно чистоњ вод€ноњ пари з дом≥шками пов≥тр€ на пучц≥ труб, €кий поперечно омивавс€, потоком сум≥ш≥. ѕучок збиравс€ з дес€ти р€д≥в труб д≥аметром 11 ≥ 19 мм з розм≥щенн€м труб по вершинам р≥вностороннього трикутника. ѕовздовжн≥й в≥дносний крок становив s2 = 1,09d.
Ќапр€мок руху пари через пучок зм≥нювавс€ в≥д низх≥дного (β = +90∞) до висх≥дного (β = Ц90∞). “руби розм≥щувалис€ €к горизонтально (θ = 0∞), так ≥ з нахилом до горизонту (θ = 10∞). “иск пари ≥ паро-газовоњ сум≥ш≥ на вход≥ складав р0 =0,0089...0,108 ћѕа; вм≥ст пов≥тр€ εг0 = 0,001...0,3; масова швидк≥сть (ρw)пг0 зм≥нювалас€ в≥д 0,7 до 15 кг/(м2Јс); середн≥й температурний нап≥р, розраховувавс€ €к р≥зниц€ температур потоку на вход≥ ≥ температури ст≥нки ≥ становив 1...70 .
ƒосл≥дн≥ дан≥ апроксимуютьс€ емп≥ричною залежн≥стю:
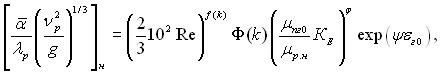 (12.35)
(12.35)
де 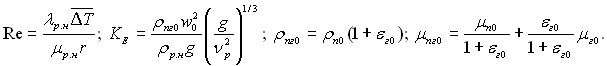
‘≥зичн≥ параметри паропов≥тр€ного потоку мають ≥ндекс УпгФ, пари УпФ, пов≥тр€ УгФ визначаютьс€ за станом на вход≥ до пучка Ц ≥ндекс У0Ф; ф≥зичн≥ властивост≥ конденсату УрФ, а також теплота фазового переходу r в≥днесен≥ до стану насиченн€ УнФ визначаютьс€ за парц≥альним тиском
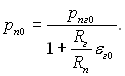
—ередн≥й коеф≥ц≥Їнт теплов≥ддач≥ розраховуЇтьс€ по формул≥:
![]()
Ўвидк≥сть w0 розраховуЇтьс€ по середньому вузькому поперечному перер≥зу пучка. ƒопом≥жн≥ функц≥њ апроксимован≥ наступними виразами:
![]() (12.36)
(12.36)
![]() (12.37)
(12.37)
![]() (12.38)
(12.38)
![]() (12.39)
(12.39)
¬еличина
φ Ц
дл€ перших пТ€ти по ходу пари р€д≥в труб зменшуЇтьс€ приблизно в≥д 0,25 до 0,1.
ƒл€ вс≥х ≥нших р€д≥в φ = 0,1. „ерез F*
позначаЇтьс€ в≥дносна поверхн€ F/F0*, де ![]() s0 Ц середн≥й перер≥з м≥ж трубами у пучц≥.
s0 Ц середн≥й перер≥з м≥ж трубами у пучц≥.
ƒл€ функц≥њ ψ запропонована наступна залежн≥сть:
Цψ = ψпг(β) + 0,03θ, (12.40)
де
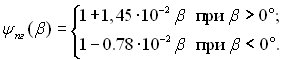
«наченн€ кут≥в θ ≥ β п≥дставл€ютьс€ в градусах, при цьому β Ц з≥ своњм знаком.
¬ област≥ 0,5Ј10Ц3 < Re ≤ 6Ј10Ц3 залежн≥сть (12.35) можна записати в наступному вигл€д≥:
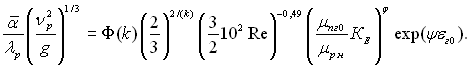 (12.41)
(12.41)
« розгл€нутого матер≥алу можна прийти до висновку, що невеликий нахил трубного пучка в≥дносно горизонтал≥ ≥нтенсиф≥куЇ конденсац≥ю пари у пучц≥.