Розділ 13. ТЕПЛООБМІН ПРИ КРАПЕЛЬНІЙ КОНДЕНСАЦІЇ ПАРИ
13.1. Ліофобізація
Для отримання крапельної конденсації необхідно, щоб когезія (зв’язування, зчеплення) конденсату була більшою за адгезію (прилипання) до металу теплообмінної поверхні. Пари ряду речовин самочинно утворюють крапельну конденсацію. Наприклад, у крапельній формі відбувається конденсація пари ртуті на нержавіючій сталі. Крапельна конденсація спостерігається і у суміші деяких парів інших речовин.
Водяна пара при конденсації на чистих металевих поверхнях дає плівкову конденсацію. Незмочування металу досягається нанесенням на його поверхню активних речовин – ліофобізаторів, молекули яких побудовані асиметрично з полярних і неполярних груп. При адсорбції таких молекул твердою фазою полярна група спрямовується в бік більш полярної твердої фази, я неполярна фаза контактує з парою. Поверхнева активність збільшується зі збільшенням асиметрії адсорбованої молекули.
В якості ліофобізаторів застосовують різні органічні сполуки полярно-неполярної будови, які поряд з неполярною чисто вуглеводневою частиною містять полярні, активні групи типу =S–SH, =Se, –SCN, –PS, –NH2, –OH, –COOH та ін. Ці групи обумовлюють зв’язок молекул з металом, неполярні ж “хвости” утворюють водо відштовхуючий “частокіл” (“частокіл” Ленгмюра) – рис.13.1.
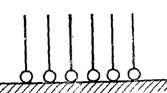
Рис.13.1. Водо відштовхуючий “частокіл” Ленгмюра
Максимальну гідрофобність забезпечують мономолекулярні шари з чітко вираженими неполярними вуглеводневими частинами не дуже великих молекул. Нанесення на поверхню теплообміну мономолекулярного шару гідрофобізатора не до додаткового термічного опору.
Основні технічні вимоги, які ставляться до ліофобізаторів, зводяться до наступного.
При достатніх теплових потоках і ступені ліофобності поверхні характерною особливістю конденсації є безперервне виникнення, природний ріст за рахунок конденсації, злиття і видалення крапель з поверхні теплообміну. Досягнення відривного розміру, при якому крапля скочується під дією сили тяжіння, відбувається внаслідок великої кількості елементарних зливань.
Ймовірністю акту злиття можна вважати функцію густини розташування крапель на поверхні ліофобного тіла і швидкості конденсації пари на окремих краплях (чи краплях з прилеглими ділянками). Як показано у восьмому розділі, ймовірність утворення на певній ділянці нової фази збільшується зі збільшенням переохолодження пари, тобто з ростом температурного напору. Швидкісна кінозйомка процесу конденсації водяної пари зі збільшенням через мікроскоп показує, що дрібні краплі ростуть швидко, далі швидкість росту стає незначною. На поверхні теплообміну, яка вивільняється після злиття окремих крапель, виникають нові дрібні краплі, які можна спостерігати починаючи з розмірів порядку мікрометра, і процес повторюється. Утворені крупні краплі скочуються з поверхні стінки.
Розрізняються два види конденсатних утворень, які знаходяться на поверхні ліофобного тіла. Кожне з цих утворень характеризується розмірами, відповідно більшими чи спів розмірними з відстанями дії міжмолекулярних сил. До перших відносяться крупні краплі, товсті плівки, до других – дрібні краплі, тонкі плівки (на стику крупних крапель стінка – пара – рідина можуть проявлятися ефекти тонких плівок). Товсті і тонкі плівки можуть бути неоднорідними по товщині, що дозволяє розповсюдити поняття плівки і на краплі.
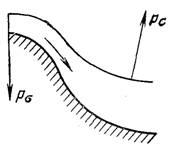
Рис.13.2. Схема капілярної течії
Розглянемо можливий вплив неоднорідності поверхні, на якій відбувається конденсація пари. Врахуємо геометричну неоднорідність. Профілографи поверхні металевої стінки свідчать про безперервну переміжність заглиблень і виступів. Виділимо достатньо малий елемент поверхні, який складається з виступу і западини (рис.13.2). У початковий момент конденсації плівка рідини, яка утворилася на цьому елементі, має товщину недалеку від товщини стійкого адсорбційного шару δ≥δ0).
Як показано в § 8.2, більш ймовірно що плівка інтенсивніше росте у впадинах. Тут, при інших рівних умовах, шар повинен бути товстішим. Різниці в товщина не змочуваної плівки повинна привести до течії плівки за рахунок градієнту тиску розклинення з області малої товщини до великої. Аналогічним чином діють капілярні сили першого роду. Врахування градієнту капілярних сил дозволяє відмовитися від припущення про початкову нерівномірність товщини плівки в западинах і на виступах, яка неминуче виникає під час конденсації. Така течія плівки приводить до утворення із зародкової плівки зародкової краплі з подальшим її ростом.
Сили, які виникають за певних умов у розглядуваному процесі, можуть бути дуже великими. Утворення зародку краплі повинно відбуватися практично миттєво і одночасно з ростом плівки. Непрямими дослідженнями є підтвердження цього явища великою швидкістю злиття окремих краплин. В дослідах з мікро кінозйомкою процесу конденсації водяної пари при експозиції кадра приблизно 0,001 с не вдалося прослідкувати акти злиття. Реєструвалися тільки початкові і кінцеві стани крапель, що зливалися.
Запропонована схема утворення зародкових крапель повинна бути найбільш різко вираженою при великих переохолодженнях пари ΔТк. Можна припустити, що при великих температурних напорах (чи малих ΔТк), коли швидкість утворення конденсату стає більшою за швидкість його стоку в краплю (чи рівна їй), на поверхні стінки між краплями може існувати нерівномірна по товщині і кривизні плівка конденсату, який безперервно флуктує у часі.
Якщо швидкість відведення рідини перевищує швидкість конденсації, на поверхні теплообміну будуть реєструватися тільки краплеподібні частинки. Таке явище можна спостерігати при конденсації ртутного пари.
Таким чином, тонку плівку на ділянках між зростаючими і краплями, які зливаються між собою, можна уявити тільки в динаміці. Площі які зайняті тонкою плівкою і товстою (краплями), повинні оцінюватися як середні у часі величини. Якщо крапля утворюється внаслідок згортання тонкої плівки, то існування останньої під час конденсації не викликає сумніву. У подальшому можна тільки обговорювати питання про питому вагу кожного з відмічених складових процесу.
Аналогічно геометричній неоднорідності можуть діяти і неоднорідності структури поверхні стінки і інші фактори, які впливають на величину капілярних сил, що, безумовно, ускладнюють питання визначення числа центрів зародкоутворення.
Згідно Я.І.Френкелю при конденсації на ідеально однорідній з фізико-хімічної точки зору ліофобній поверхні стінки повинні виникати розриви плівки, які носять флуктуаційний характер. Положення точки розриву у цьому випадку не фіксується на поверхні. Питання динамічної нестійкості плоских плівок розглядалися рядом авторів, внаслідок чого отримане рівняння розриву:
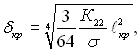
де δкр – критична товщина плівки; ℓ – довжина хвилі випадкового подразнення; σ – поверхневий натяг. При фіксованому значенні δ до розриву плівки ведуть подразнення з довжиною хвилі ℓ > ℓкр.
Якщо використати наведену формулу для розрахунку ℓкр при значенні δкр = 0,63 мкм, отриманому в роботі Сугавари і Кацути, то значення ℓкр буде на декілька порядків більшим за ті, що спостерігалися. Ця обставина дозволяє вважати, що основною причиною розриву плівки з послідовним стягуванням у краплі є відмічена раніше фізико-хімічна неоднорідність поверхні.
У тому випадку, коли можна говорити про конкретний розподіл неоднорідності, первинні краплі будуть спостерігатися в певних місцях цієї поверхні. Таким чином, з’являється можливість говорити про фіксовані центри конденсації. Очевидно, ріст крапель і як наслідок їх злиття, які спостерігаються при конденсації водяної пари, приведуть до нових комбінацій розміщення крапель на поверхні тіла.
Особливий інтерес викликає вплив теплової неоднорідності поверхні конденсації. Якщо температура поверхні розділу фаз змінна, то повинні проявлятися термокапілярні сили. При крапельній конденсації температура стінки змінюється в часі і по поверхні (просторі). Пульсації температури пояснюються змінним термічним опором конденсованої фази (у багатьох випадках можуть бути наслідком процесу теплообміну з боку охолоджувального агента).
Виходячи з можливості суперпозиції ефектів, обумовлених капілярними силами першого і другого роду, для тангенціальної термокапілярної сили можна записати:
(13.1)
де ξ, ζ – відповідно температурні коефіцієнти поверхневого натягу і тиску розклинення. При δ→∞ маємо Π→0, при ptn→0 і pt→ptσ, тобто актуальними є тільки термокапілярні сили першого роду.
Оцінка залежності тиску розклинення від температури можна представити наступним чином, так при δ ≥ 10–5 м для плівки води, яка знаходиться на ідеальному діелектрику, ця залежність достатньо велика і становить:
Якщо виходити із залежності П = δ3 і тангенціальну зміну температури прийняти рівною по порядку нормальній зміні ΔТ/δ, де ΔТ – температурний напір на даній ділянці, то
Згідно цього рівняння величина рtn суттєво залежить від температури. Це дозволяє вважати, що при згортанні плівки у краплю на певній стадії цього процесу до дії можуть вступити і термокапілярні сили. Температурний коефіцієнт тиску розклинення для плівок товщиною до 6·10–7 дуже малий чи рівний нулю. Відсутність залежності тиску розклинення дуже тонких плівок від температури у випадку коректності застосування теорії свідчить про те, що розташування перерізів розриву не залежить від пульсацій температури.
Відмітимо можливості зміни фізичних властивостей речовини, яка входить до складу тонкої плівки у порівнянні з масивом цієї рідини. При перебуванні речовини у внутрішніх силових полях суміжних фаз можуть змінюватися такі властивості, як коефіцієнт в’язкості, теплопровідності, густина та ін.
Можна вважати, що при довготривалому процесі в западинах може затримуватися рідина. Внаслідок цього вплив тонких плівок в певній мірі слабшає. Крім геометричної неоднорідності ймовірність появи нової фази чи необхідне переохолодження пари можуть залежати від структурної неоднорідності поверхневого шару твердого тіла, викликаних розривом ліофобних властивостей на окремих ділянках.
Вплив таких дефектів носить подвійний характер. Якщо дефекти обумовлюють зменшення роботи утворення зародка, то у цьому разі можна чекати появу життєздатної нової фази (для активного проходження крапельної конденсації розміри таких ділянок повинні бути спів розмірними з рівноважними розмірами зародка).
Таким чином, можливість виникнення первинних утворень рідкої фази на ліофобній поверхні залежить від великої кількості факторі. Але в усіх випадках ймовірність утворення зародків пропорційна переохолодженню пари (температурному напору). Враховуючи, що коефіцієнт пропорційності є функцією розглянутих раніше факторів (таких, як мікро геометрична неоднорідність, неоднорідність структури та ін.), то можна знайти особливі ділянки поверхні, які забезпечують початок конденсації як при порівнянно малих температурних напорах, так і при великих переохолодженнях ΔТк. Середні характеристики процесу (такі, як кількість зародків, що утворюються в одиницю часу на одиничній поверхні, середнє переохолодження та ін.) повинні розглядатися як середньостатистичні величини.
Ефекти злиття крапель відіграють значну роль в процесах крапельної конденсації, забезпечуючи швидку появу на поверхні теплообміну крапель з відривним значенням радіуса. При цьому звільняється частина поверхні теплообміну. Дисперсна фаза має велику поверхню контакту з паром і менший термодинамічний опір. Досягнення відривного розміру внаслідок об’єднання більш дрібних крапель повинно забезпечувати значну середню інтенсивність процесу конденсації в порівнянні з автономним ростом крапель.
Таким чином, масове злиття крапель можна розглядати як одну з причин інтенсифікації процесу теплообміну. При цьому звільняється певна кількість центрів конденсації і процес повторюється.
З урахуванням термічного опору теплопровідності плівки можна написати:
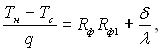
де Тс – температура стінки; λ – коефіцієнт теплопровідності плівки, який в першому наближенні дорівнює коефіцієнту теплопровідності масиву рідини. Вважаємо, що коефіцієнт конденсації f = 1
Із співставлення величин RфRф1 і δ/λ слідує, що, наприклад, при конденсації пари атмосферного тиску термічний опір плівки стає суттєвим при товщині біля 10–7 м. Роль фазового опору збільшується при зменшенні тиску.
Отже, при крапельній конденсації водяної пари невеликого тиску на ділянках, зайнятих тонкою плівкою, сумарний термічний опір в основному обмежується термічним опором фазового переходу. Роль фазового опору збільшується зі зменшенням коефіцієнта конденсації.
Виконаний аналіз показує, що роль ефектів капілярності другого роду своєрідна і порівнянно обмежена. Ефекти такої плівки в основному актуальні для механізму гетерогенного утворення зародка рідкої фази. Якщо вважати, що всі необхідні характеристики центрів конденсації чи зародків (наприклад, їх поверхнева густина, розміри, частота утворення та ін.) задані, то при вивченні теплообміну роль капілярних ефектів другого роду може бути зведеною до мінімуму.
Дійсно, тиск розклинення актуальний тільки для тонких плівок і крапель, при цьому ж основним термічним опором є термічний опір фазового переходу. Рухомість рідкої фази, викликана тиском розклинення, не повинна проявлятися в сумарних характеристиках термічного опору конденсату.
Фазовий опір втрачає свою актуальність при порівнянно великих товщина рідкої фази. При цьому рухомість конденсату повинна бути обумовлена поверхневим натягом (пара вважається практично нерухомою). У той же час ймовірність утворення нової фази залежить від особливих властивостей тонкої плівки.
13.3. Статистичні характеристики
13.3.1. Рівняння теплообміну
Розглянемо в середньому усталений процес. Маючи задану кількість центрів конденсації і початковий розмір крапель, можна нехтувати початковою стадією утворення рідкої фази. Вважаємо, що поверхня краплі, яка знаходиться в контакті з парою, є сферичною. Її кривизна може оцінюватися радіусом R. Також будемо вважати, що стінці передається тільки виділена теплота фазового переходу.
Тепловий потік, обумовлений ростом одиничної напівсферичної краплі за рахунок конденсації (за рахунок природного росту), знайдемо як добуток зміни її маси в одиницю часу на питому теплоту фазового переходу:
На поверхні теплообміну одночасно існують безліч крапель з радіусами, які змінюються від початкового Rn до радіуса R0, що відповідає відриву краплі. Таке розмаїття можна характеризувати диференціальною функцією розподілу крапель за розмірами φ(R) = dn/dR, де dn – кількість крапель з інтервалу (R, R+dR), що знаходяться на одиниці поверхні стінки. В середньо усталеному процесі усталена і функція розподілу.
Густина теплового потоку на поверхні стінки, обумовлена конденсацією на краплях з інтервалу (R, R+dR), буде:
де лінійна швидкість росту краплі dR/dτ позначена через w(R) і враховано, що dn = φ(R)dR.
Інтегруючи цей вираз в межах від Rn до R0 і враховуючи теплоту, яка виділяється при утворенні крапель з радіусом Rn, отримаємо наступне рівняння теплообміну:
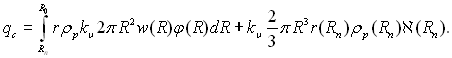(13.2)
Коефіцієнт kυ введений до рівняння (13.2) для урахування можливого відхилення форми поверхні краплі від напівсферичної; при крайовому куті θ = 90° kυ = 1. Функція א(R) = w(R)φ(R) показує кількість крапель на одиниці поверхні стінки, які пересікають за одиницю часу границю R. Зазвичай величина R0 на декілька порядків перевищує Rn. Нехтуючи другим доданком в (13.2), можна написати:
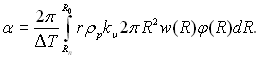(13.3)
У цьому рівнянні α є середній в часі коефіцієнт тепловіддачі. Ураховуючи досить великі розміри і дискретність крапель, слід вважати, що коефіцієнт тепловіддачі згідно (13.3) є середньою величиною на певній ділянці поверхні, яка містить велику кількість крапель.
Таким чином, задача визначення середнього коефіцієнта тепловіддачі зводиться до визначення функції א(R) = w(R)φ(R). Значення функції א(R) повинно бути пов’язане з безперервними процесами злиття крапель. Злиття буде актуальним у разі, якщо густина розміщення крапель на поверхні стінки достатньо велика.
Для аналітичного визначення qc рівняння (13.2) необхідно доповнити рівнянням, яке описує невідому функцію א(R) [чи φ(R), якщо w(R) задається]. Таким рівнянням може бути рівняння рівноваги. При усталеному середньому процесі кількість крапель dn, м–2, в інтервалі (R, R+dR) є незмінною величиною. Між зникненням і виникненням крапель в інтервалі dR повинна установитися динамічна рівновага.
Позначимо через dξ+ число крапель, які потрапляють в одиницю часу в інтервал dR внаслідок злиття більш дрібних крапель; dξ– – число крапель, які покидають інтервал dR внаслідок злиття з іншими краплями чи одна з іншою.
При усталеному випадковому процесі
(13.4)
Рівняння (13.4) формулює умови детальної (лічильної) рівноваги. Для визначення функцій ξ+ і ξ– необхідно знайти число зливань крапель різних розмірів.
Вважаємо, що відбувається попарне злиття крапель. Краплі зливаються миттєво після первинного дотику одна з іншою. Ймовірність злиття крапель залежить від густини їх розміщення на поверхні конденсації і швидкості конденсаційного переміщення фронту крапель
де Rsinθ – радіус основи крапель; θ – крайовий кут. Виведемо рівняння лічильної рівноваги, вважаючи, що зштовхування відбуваються за рахунок природного росту крапель. При цьому виходимо з умови, що θ ≤ 90°, вважаючи, що крайовий кут фіксований, тобто не залежить від процесу. При розгляді випадку θ > 90° не виникає принципових ускладнень, але геометричні співвідношення трохи ускладнюються.
Для певного моменту часу з інтервалу (R, R0) довільно вибираємо дві краплі з радіусами Rр Rq і розглянемо умови, за які задовольняють взаємне розташування крапель, щоб на протязі наступного проміжку часу dτ відбулося їх зштовхування. Очевидно, відстань між центрами основ крапель не повинно перевищувати величину
де dRр = w(Rp)dτ і dRq= w(Rq)dτ .
Мінімальна відстань між центрами основ крапель дорівнює:
Краплі з інтервалом (Rр, Rр+dRр), центри яких знаходяться всередині комірки з радіусами, рівними ℓмакс і ℓмін зазнають за час dτ зштовхування з одиничною краплею з інтервалу (Rq, Rq+dRq).
Оскільки функція розподілу φ(Rр) ≡ dnpdnp/Rp віднесена до одиниці поверхні, то число крапель розміром (Rр, Rр+dRр), які приходяться на площу кільця, становить:
(13.5)
Така сама кількість зштовхувань відбудеться між одиничною краплею з радіусом Rq і краплями з радіусом Rр за час dτ. Оскільки на одиницю поверхні приходиться φ(Rq)dRq крапель з радіусом Rq, , то в одиницю часу на одиниці поверхні відбувається наступна кількість зштовхувань:
(13.6)
Виконавши заміну φ = א/w, отримаємо наступний вираз для кількості зливань dξ крапель Rp і Rq:
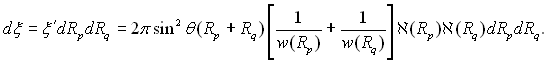(13.7)
Радіуси утворених крапель R і вихідних крапель Rp і Rq зв’язані рівнянням
R3 = R3p + R3q. (13.8)
Мінімальний і максимальний радіуси крапель, утворених при злитті, дорівнюють відповідно:
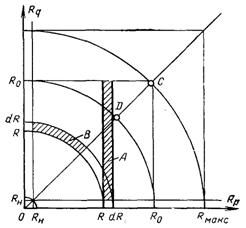
Рис.13.3. До виводу рівняння лічильної рівноваги
Зобразимо окремий акт злиття крапель Rp і Rq точкою на площині (Rp, Rq) – рис.13.3. Криві на графіку (Rp, Rq) побудовані по рівнянню (13.8). Довільна точка на цих кривих відповідає злиттю крапель Rp, Rq з утворенням краплі R. Точки, розташовані всередині елементарної площадки А, відповідають злиттю крапель (R, R+dR) з краплями різних розмірів в інтервалі RО(Rп, R0). Вважаємо, що краплі R >R0 миттєво видаляються після утворення і не приймають участь в подальших злиттях.
Точки, які розташовані всередині елементарної області В відповідають таким злиттям, внаслідок яких утворюються краплі (R, R+dR). Точкам на діаграмі (Rp, Rq) відповідають згідно рівнянню (13.7) певні значення частоти злиття ξ′. На підставі сказаного про зміст областей А і В можна записати:
(13.9)
Підставляючи у рівняння (13.4) отриманий вираз (13.9), отримаємо наступний вираз лічильної рівноваги:
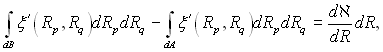(13.10)
де функція ξ'. визначається за рівнянням (13.7).
При великій щільності розміщення крапель на поверхні стінки частота зштовхувань збільшується. Цю обставину можна врахувати введенням в (13.7) множника 1/(1 – Fк), де Fк – доля поверхні, яка зайнята краплями. У цьому разі для частоти злиття крапель ξ' можна записати
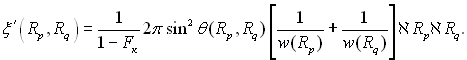(13.11)
У граничному випадку, коли частота злиття крапель дуже мала, розв’язок рівняння цифрової рівноваги (13.10) має елементарний вид:
(13.12)
13.3.3. Рівняння народження крапель
Рівняння народження крапель відіграє роль граничної умови, з якої визначається стала інтегрування рівняння (13.10). Якщо центри конденсації із середньою щільністю N, м–2, довільно розташовані на поверхні теплообміну, то внаслідок злиття, а також при скочуванні крапель з радіусом R ≥ R0 в одиницю часу вивільняється певна кількість центрів конденсації, на яких виникають краплі з радіусом Rn. Величина א(R) має зміст лічильного потоку крапель, які пересікають границю R під час росту. У процесі утворення первинних крапель злиття не відіграє ніякої ролі. Внаслідок цього можна частоту виникнення первинних крапель ототожнити з величиною א(Rп). Приріст площі контакту краплі зі стінкою за одиницю часу буде:
Приріст контактної площі всіх крапель визначається з виразу:
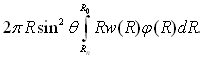
Останній вираз визначає також вивільнену в одиницю часу поверхню контакту, що обумовлено в середньому усталеністю процесу. Повна відносна поверхня Fк, що зайнята краплями становить:
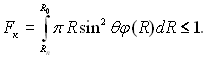(13.13)
Під час виникнення первинних крапель з радіусом Rn злиття не має ніякого значення. Кількість вивільнених в одиницю часу центрів конденсації дорівнює кількості первинних крапель з радіусом Rn, які виникли за цей же проміжок часу. За цих умов можна записати:
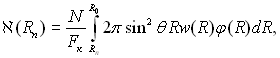(13.14)
чи, з урахуванням виразу (13.13),
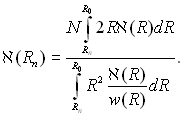(13.15)
Для розв’язку системи рівнянь (13.10) і (13.15) з наступним визначенням потоку теплоти за (13.2) необхідно задати значення Rn, R0, w(R) і N. Ці величини повинні визначатися, виходячи з фізичних міркувань і експериментальних досліджень теплообміну при крапельній конденсації.
