




13.4. Ўвидк≥сть росту крапл≥
ѕрирощенн€ рад≥уса крапл≥, обумовлене конденсац≥Їю пари на њњ в≥льну поверхню, нерозривно повТ€зане з тепловим потоком. “епловий пот≥к через поверхню крапл≥ пара Ц р≥дина можна визначити за р≥вн€нн€м
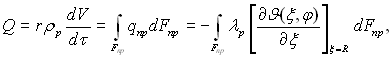
де J(ξ, φ) Ц температура крапл≥ €к функц≥€ пол€рного рад≥уса ξ ≥ широти φ.
”раховуючи, що
![]()
де ψ Ц довгота, ≥ що дл€ нап≥всферичноњ крапл≥
![]()
можна записати:
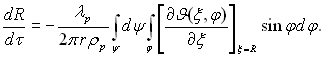
≤нтегруючи по ψ ≥ φ в≥дпов≥дно в межах в≥д 0 до 2π ≥ в≥д 0 до π/2, отримаЇмо:
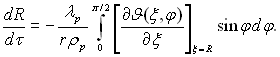 (13.16)
(13.16)
–≥вн€нн€ (13.16) записане з припущенн€м, що крапл€ Ї нап≥всферичною ≥ що температурне поле у крапл≥ Ї функц≥Їю т≥льки пол€рного рад≥уса ≥ широти. ¬≥д довготи температура не залежить. «апишемо математичне формулюванн€ задач≥ дл€ температурного пол€ в крапл≥, вважаючи, що теплота переноситьс€ т≥льки теплопров≥дн≥стю. –≥вн€нн€ теплопров≥дност≥ у сферичних координатах буде:
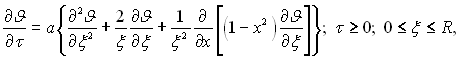 (13.17)
(13.17)
де х = cosφ.
ѕочатков≥ умови:
![]() (13.18)
(13.18)
√раничн≥ умови:
![]() (13.19)
(13.19)
![]() (13.20)
(13.20)
ћатематичне формулюванн€ задач≥ дл€ швидкост≥ росту крапл≥, представлене виразами (13.16)...(13.20), спрощене дл€ њњ можливост≥ реал≥зац≥њ на практиц≥. Ќе дивл€чись на зроблен≥ спрощенн€, сформульована задача залишаЇтьс€ достатньо складною. “а обставина, що R ≠ const, суттЇво њњ ускладнюЇ. ћетоди р≥шенн€ таких задач, €к≥ належать до класу задач —тефана, розроблен≥ недостатньо.
—тац≥онарне температурне поле в нап≥всферичн≥й крапл≥ з ф≥ксованими границ€ми ≥ ф≥ксованими значенн€ми граничних температур
Jпов = const ≥ Jс = 0 (13.21)
описуЇтьс€ наступним р≥вн€нн€м:
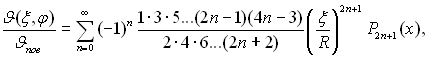 (13.22)
(13.22)
де Pk(x) ≡ Pk(cosφ) Ц пол≥ном Ћагранжа першого роду k-го пор€дку. ѕол≥номи Ћагранжа берутьс€ дл€ непарних значень k = 2n + 1 ≥ т≥льки при цьому задовольн€Їтьс€ умова Jс = 0.
—тац≥онарне температурне поле у крапл≥, €ка маЇ форму сферичного сегменту, можна описати при граничних умовах Jпов = const ≥ Jс = 0 р≥вн€нн€м:
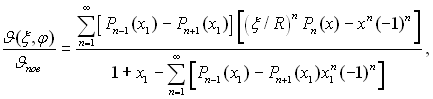 (13.23)
(13.23)
де х1 = cosθ, θ Ц крайовий кут. ƒл€ випадку θ = π/2 останнЇ р≥вн€нн€ переходить в (13.22).
“епловий пот≥к зг≥дно (13.23) визначаЇтьс€ з формули
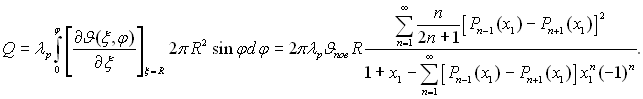
(13.24)
«а умови ф≥ксованих ≥ незм≥нних по поверхн≥ значень Jпов ≥ Jс р≥вн€нн€ (13.22) ≥ (13.23) мають певн≥ особливост≥. ѕри φ= π/2 маЇ м≥сце розрив температурного пол€ ≥, €к насл≥док, нульовий терм≥чний оп≥р. јнал≥з р≥вн€нь (13.22) ≥ (13.23) показуЇ, що неск≥нченн≥ р€ди Ї розб≥жними. ” той же час безмежно велик≥ значенн€ Q ≥ dR/dτ ф≥зично не обірунтован≥ ≥ позбавлен≥ лог≥чного зм≥сту. ѕрактично швидк≥сть росту крапл≥ к≥нцева величина. Ќеск≥нченно велика теплопров≥дн≥сть крапл≥ завжди обмежена к≥нцевим м≥ж фазним опором. «адача про перенесенн€ теплоти краплею, €ка представл€Ї собою сегмент сфери, при Jпов = const ≥ Jс = 0 розвТ€зана методом к≥нцевих р≥зностей, при цьому тепловий пот≥к на д≥л€нц≥, зайн€т≥й краплею, можна описати наступним р≥вн€нн€м:
![]() (13.25)
(13.25)
де d Ц д≥аметр основи крапл≥; f2(θ) Ц функц≥€ крайового кута, €ка Ї монотонною вв≥гнутою в≥дТЇмною кривою, €ка зм≥нюЇтьс€ в≥д f2(20∞) = 35 до f2(140∞) = 5. ƒл€ θ = 90∞ f2(θ) = 8. ” цьому раз≥ дл€ нап≥всферичноњ крапл≥ маЇмо:
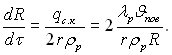 (13.26)
(13.26)
ѕропускаючи питанн€ про сходженн€ р€ду ≥ обмежуючись дес€тьма членами, такий же вираз можна отримати дл€ dR/dτ ≥з (13.24).
–озгл€немо теплопров≥дн≥сть через нап≥всферичну поверхню при граничних умовах третього роду. ѕостановка задач≥ аналог≥чна (13.22), але граничну умову J(R) = Jпов зам≥нимо наступною умовою
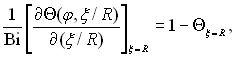
де 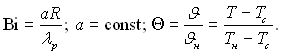
як ≥ в попередньому випадку ![]()
«агальний розвТ€зок, очевидно, не зм≥нитьс€ ≥ становить:
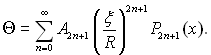
¬раховуючи граничну умову дл€ поверхн≥ пара Ц р≥дина, можна записати:
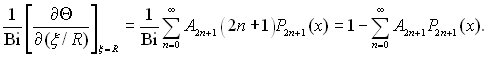
«в≥дки 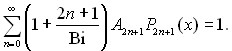
оеф≥ц≥Їнт р€ду:
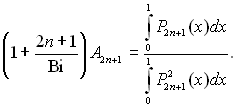 (13.27)
(13.27)
≤нтеграл знаменника останнього р≥вн€нн€, при т = k приймаЇ вид:
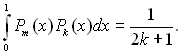
“ому що т = 2п + 1, 2(2п +1) + 1 = 4п + 3, то
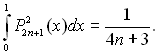 (13.28)
(13.28)
≤нтеграл, €кий стоњть у чисельнику (13.27), можна виразити через гама-функц≥ю
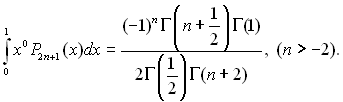 (13.29)
(13.29)
¬≥домо, що √(1) = 1, √(1/2) = π0,5 ≥ √(п +1/2) = (π0,5/2п)(2п Ц 1)!. ‘ункц≥ю √(п + 2) можна представити наступним чином √(п + 2) = (п + 1)!. ѕ≥дставл€ючи значенн€ гама-функц≥њ в≥д аргумент≥в 1/2; 1; п + 1/2 ≥ (п + 2) в (13.29), отримаЇмо:
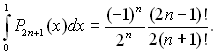 (13.30)
(13.30)
”раховуючи (13.28) ≥ (13.30), отримаЇмо:
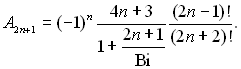
¬насл≥док виконаних спрощень ≥ перетворень отримаЇмо:
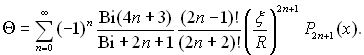 (13.31)
(13.31)
ƒл€ використанн€ таблиць гама-функц≥й можна записати, що
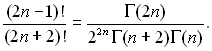
ѕри ¬≥ → ∞ р≥вн€нн€ (13.31) переходить у р≥вн€нн€ (13.22) отримане при граничних умовах першого роду. « р≥вн€нн€ (13.31) виходить, що
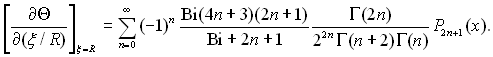 (13.32)
(13.32)
“епловий пот≥к через поверхню нап≥всферичноњ крапл≥ пара Ц р≥дина буде:
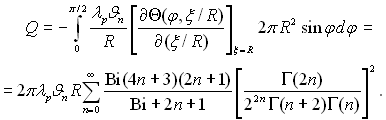 (13.33)
(13.33)
” випадку, коли ¬≥ → ∞ маЇмо [1 + (2п + 1)/¬≥] → 1 ≥ отримуЇмо р≥шенн€ при граничних умовах першого роду:
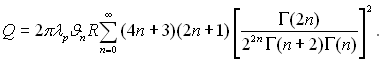 (13.34)
(13.34)
“аким чином, розвТ€зок при граничних умовах першого роду в≥др≥зн€Їтьс€ значенн€ми коеф≥ц≥Їнт≥в р€ду Ц вони зб≥льшен≥ в [1 + (2п + 1)/¬≥] раз≥в.
« р≥вн€нн€ (13.33) ≥ р≥вн€нн€
![]()
сл≥дуЇ, що
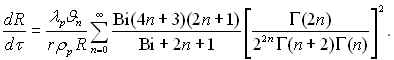 (13.35)
(13.35)
” випадку, коли ¬≥ → ∞ маЇмо з (13.35):
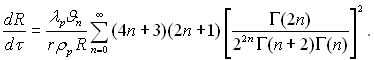 (13.36)
(13.36)
« наведених формул сл≥дуЇ, що швидк≥сть росту крапл≥ обернено пропорц≥йна рад≥усу. –≥вн€нн€ (13.35) через число Ѕ≥о ¬≥ враховуЇ €к теплопров≥дн≥сть крапл≥, так ≥ терм≥чну пров≥дн≥сть пари. ќстанн€ може складатис€ з величин зворотних м≥жфазному ≥ дифуз≥йному опорам.
–ан≥ше наведен≥ р≥вн€нн€ швидкост≥ росту крапл≥ отриман≥ дл€ усталених температурних пол≥в. ÷€ обставина вимагаЇ досл≥дноњ перев≥рки отриманих формул. р≥м цього, у загальному випадку в крапл≥ може виникати конвекц≥€.
Ћ≥н≥йна швидк≥сть безперервного росту dR/dτ експериментально досл≥джувалас€ в р€д≥ роб≥т. ” де€ких роботах виконувалас€ швидк≥сна к≥нозйомка з≥ зб≥льшенн€м через м≥кроскоп процесу крапельноњ конденсац≥њ вод€ноњ пари з тиском приблизно 0,1 ћѕа. √≥дрофоб≥затор Ц олењнова кислота, октадец≥лселеноц≥ан≥д. –озд≥льна здатн≥сть оптичноњ системи дозвол€ла просл≥дкувати т≥льки за ростом достатньо крупних крапель (R > 3 мкм). ¬им≥рюванн€ розм≥р≥в крапель заф≥ксованих на к≥нопл≥вц≥, виконувалос€ з допомогою ≥нструментального м≥кроскопа. адри було в≥дзн€т≥ при температурних напорах 0,8...2,5 .
–≥ст крапель просл≥джувавс€ в≥д кадра до кадра посл≥довно до моменту дотиканн€ чи злитт€ ≥з сус≥дн≥ми крапл€ми, п≥сл€ цього в≥дбувалос€ стрибкове зб≥льшенн€ розм≥ру. ¬изначенн€ мит≥ злитт€ ≥нколи затрудн€лос€ ≥з-за великоњ частоти зливань. ѕри цьому не можливо було ф≥ксувати злитт€ з б≥льш др≥бними крапл€ми, розм≥ри €ких знаходилис€ за межами розд≥льноњ здатност≥ оптичноњ системи.
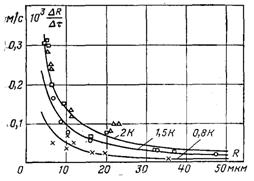
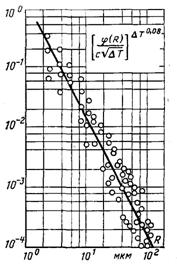
–ис.13.4. «алежн≥сть швидкост≥ безперервного росту крапл≥ в≥д рад≥уса: крив≥ Ц розрахунок за (13.26); точки Ц досл≥дн≥ значенн€ при Δ“, : £ Ц 2,0; Щ Ц 1,5; ќ Ц 0,8; r Ц 2,5
«алежн≥сть швидкост≥ безперервного росту крапель в≥д рад≥уса R( = 0,5(Rпоч + R) наведена граф≥чно на рис.13.4. рив≥ побудован≥ на п≥дстав≥ розрахунк≥в за (13.26) дл€ трьох значень температурного напору. ¬еличина R( Ї середньою величиною за цикл безперервного росту рад≥уса крапл≥.
як видно з рис.13.4 л≥н≥йна швидк≥сть росту крапл≥ в ≥нтервал≥ рад≥ус≥в в≥д 5 до 50 мкм апроксимуЇтьс€ р≥вн€нн€м (13.26). –озкид досл≥дних точок в≥дносно апроксимац≥йних кривих можна по€снити зб≥льшеною похибкою визначенн€ малих рад≥ус≥в ≥ можливою зм≥ною реальних початкових ≥ граничних умов у пор≥вн€нн≥ з розрахунковими. ¬арто також урахувати, що злитт€ з найб≥льш др≥бними крапл€ми не можливо було реЇструвати внасл≥док недостатньоњ розд≥льноњ здатност≥ оптичноњ системи. ѕри зб≥льшенн≥ рад≥уса зб≥жн≥сть досл≥дних ≥ розрахункових значень швидкост≥ росту пол≥пшуЇтьс€.
13.5. –озпод≥л крапель за розм≥рами
‘ункц≥€ розпод≥лу крапель за розм≥рами Ї одн≥Їю з основних характеристик крапельноњ конденсац≥њ. —проби анал≥тичного визначенн€ ун≥версальноњ функц≥њ розпод≥лу наштовхуютьс€ на велик≥ труднощ≥. ќц≥нки зроблен≥ на п≥дстав≥ л≥чильноњ р≥вноваги, показують, що характер розпод≥лу крапель за розм≥рами повинен зм≥нюватис€ в залежност≥ в≥д величини NF0, де F0 Ц площа, €ка зайн€та краплею в≥дривного рад≥уса.
” раз≥ в≥дсутност≥ злитт€ (величина NF0 мала), €к сл≥дуЇ з (13.26)
wφ = const.
якщо w ~ 1/R, що сл≥дуЇ з попереднього параграфа, то
φ(R) = constЈR. (13.37)
Ћ≥н≥йна залежн≥сть (13.37) зм≥нюЇтьс€ при зб≥льшенн€ NF0. ѕри великих NF0 функц≥€ φ(R) проходить через максимум, при цьому в м≥ру зб≥льшенн€ NF0 положенн€ точки максимуму зсовуЇтьс€ в б≥к менших рад≥ус≥в. “аким чином, ймов≥рно, що при великих значенн€х NF0 експериментальн≥ досл≥дженн€ у зв'€зку з обмеженою розд≥льною здатн≥стю можуть дати т≥льки зменшенн≥ φ(R) при зб≥льшенн≥ R.
¬иконан≥ досл≥дженн€, в €ких вод€на пара з тиском, приблизно р≥вним атмосферному, конденсувалас€ на торц≥ горизонтального м≥дного стрижн€ д≥аметром 16 мм. ќпрацьован≥ кадри отриман≥ швидк≥сною к≥нозйомкою при температурних напорах 0,4; 0,8; 1,5 ≥ 2 . ћить видаленн€ крапл≥ в≥дривного розм≥ру з наступною по€вою на кадр≥ др≥бних крапель приймалас€ за початок в≥дл≥ку пер≥оду. –озраховувалас€ величина
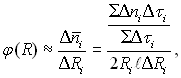 (13.38)
(13.38)
де Δп≥ Ц число крапель розм≥ром ΔRi на площ≥ 2Riℓ; Δτ≥ Ц ≥нтервал часу, €кий в≥дпов≥даЇ р≥зниц≥ м≥ж номерами кадр≥в на пл≥вц≥.
–озд≥льна здатн≥сть оптичноњ системи дозвол€Ї просл≥дкувати т≥льки за крупними крапл€ми понад 3 мкм. ‘ункц≥€ розпод≥лу приймалас€ степеневою:
![]()
Ќев≥дом≥ параметри степеневоњ залежност≥ визначалис€ методом найменших квадрат≥в. –езультати опрацюванн€ показали, що величини a ≥ b Ї функц≥€ми температурного напору.
–ис.13.5. јпроксимац≥€ досл≥дних даних з розпод≥лу крапель по розм≥рам: с Ц стала у в≥дпов≥дност≥ з формулою (13.39)
‘ункц≥€ розпод≥лу крапель за розм≥рами описуЇтьс€ наступним р≥вн€нн€м:
![]() (13.39)
(13.39)
де Δ“ = “п Ц “с, ; R Ц рад≥ус крапл≥, м.
¬ираз (13.39) разом з р≥вн€нн€ми (13.2) ≥ (13.26) було використано дл€ розрахунку густини теплового потоку ≥ коеф≥ц≥Їнта теплов≥ддач≥. ѕри цьому вважалос€, що крапл≥ мають нап≥всферичну форму. ≤нтегруванн€ виконувалос€ в межах в≥д R = 3 мкм до R = 103 мкм, що в≥дпов≥даЇ граничним значенн€м рад≥ус≥в крапель, вим≥р€них при опрацюванн≥ кадр≥в к≥нопл≥вки. ѕор≥вн€нн€ розрахункових даних з результатами пр€мих вим≥р≥в qc ≥ α дали задов≥льну зб≥жн≥сть.
13.6. “еплообм≥н при конденсац≥њ нерухомоњ чистоњ пари
ƒл€ отриманн€ достатньо над≥йних розрахункових формул, €к≥ описують крапельну конденсац≥ю, зараз здеб≥льшого приходитьс€ звертатис€ до досл≥дних даних. ѕри описуванн≥ експериментальних даних у вигл€д≥ емп≥ричних р≥вн€нь важливо ви€вити обірунтован≥ безрозм≥рн≥ параметри, €к≥ дозвол€ють з переконливою ун≥версальн≥стю описати результати досл≥д≥в.
ќсновою дл€ отриманн€ перел≥ку головних безрозм≥рних зм≥нних Ї математичне формулюванн€ задач≥. ” залежност≥ в≥д повноти њњ постановки може зм≥нюватис€ ≥ сам перел≥к безрозм≥рних зм≥нних.
ѕри крапельн≥й конденсац≥њ процес суттЇво залежить в≥д кап≥л€рних властивостей розгл€дуваноњ системи. –ухом≥сть р≥дкоњ фази повТ€зана з процесом теплообм≥ну на досл≥дн≥й д≥л€нц≥. …мов≥рн≥сть утворенн€ зародк≥в новоњ фази залежить в≥д ступен€ переохолодженн€ пари. ÷≥ характерн≥ особливост≥ процесу п≥дказують про в≥дпов≥дний виб≥р масштаб≥в при запису задач≥ в безрозм≥рному вигл€д≥. «а л≥н≥йний масштабний розм≥р можна приймати критичний рад≥ус зародка
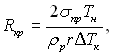
а за масштаб швидкост≥ 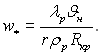
ќстанн≥й вираз можна тлумачити €к в≥дношенн€ швидкост≥ в≥дводу тепла теплопров≥дн≥стю до швидкост≥ вид≥ленн€ теплоти фазового переходу.
ѕри запису р≥вн€нн€ руху дл€ конденсату вважаЇтьс€, що град≥Їнт тиску перед ус≥м визначаЇтьс€ кап≥л€рними силами. “акож ураховуЇтьс€ залежн≥сть поверхневого нат€гу в≥д температури.
ƒл€ опису середньоњ теплов≥ддач≥ можна запропонувати наступний вираз:
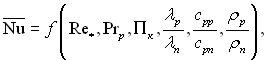 (13.40)
(13.40)
де 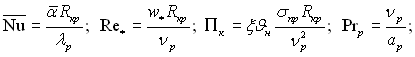 ξ Ц температурний коеф≥ц≥Їнт поверхневого нат€гу, €кий визначаЇтьс€ з р≥вн€нн€
ξ Ц температурний коеф≥ц≥Їнт поверхневого нат€гу, €кий визначаЇтьс€ з р≥вн€нн€ ![]() Jн Ц температурний нап≥р, €кий розраховуЇтьс€ €к р≥зниц€ температур насиченн€ ≥ ст≥нки.
Jн Ц температурний нап≥р, €кий розраховуЇтьс€ €к р≥зниц€ температур насиченн€ ≥ ст≥нки.
” початковий момент росту новоњ фази р≥зниц€ температур р≥дини ≥ ст≥нки м≥н≥мальна ≥ незначна. ÷е дозвол€Ї за масштаб надлишкових температур прийн€ти Jн, тобто виконати зам≥ну Δ“к на Jн.
Ѕезрозм≥рна зм≥нна ѕк враховуЇ вплив термокап≥л€рного руху. ѓњ можна тлумачити €к в≥дношенн€ тепрмокап≥л€рних сил до сил вТ€зкост≥. ¬еличину ѕк можна представити в такому вид≥:
ѕк = ξJнLp,
де Lp = σпрRкр/(ρрν2р) Ц число Ћапласа.
—имплекси, €к≥ представл€ють собою в≥дношенн€ однойменних ф≥зичних параметр≥в р≥дини ≥ пари, в≥дображають вплив на процес тепловоњ взаЇмод≥њ цих фаз. ¬плив симплекс≥в при низьких тисках не повинен бути значним.
—ереднЇ значенн€ числа Ќуссельта, чисел –ейнольдса ≥ ѕк п≥сл€ п≥дстановки в них значень w* ≥ Rкр будуть:
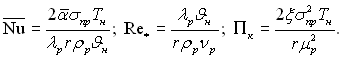 (13.41)
(13.41)
ѕерел≥к безрозм≥рних зм≥нних (13.40) не вичерпуЇ вс≥ можливост≥ впливових фактор≥в.
√рад≥Їнт тиску в пл≥вц≥ можна виразити через кап≥л€рн≥ сили:
![]() (13.42)
(13.42)
якщо використати р≥вн€нн€ виду ѕ = јδЦ3, то з формулюванн€ крайовоњ задач≥ виходить, що кр≥м числа ѕк зТ€вл€Їтьс€ близьке йому за структурою наступне число под≥бност≥:
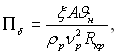 (13.43)
(13.43)
де ξ Ц температурний коеф≥ц≥Їнт тиску розклиненн€; ј Ц величина, що характеризуЇ вплив на тиск розклиненн€ ф≥зичних властивостей трьох фаз.
Ќаск≥льки число ѕδ необх≥дне при корекц≥њ даних за середньою температурою, отриманих в р≥зних за своЇю ф≥зичною природою системах т≥л (пара, п≥дкладка), можна судити т≥льки на п≥дстав≥ досл≥дних даних. Ќа€вний експериментальний матер≥ал не даЇ можливост≥ зараз вир≥шувати це питанн€ з достатньою скрупульозн≥стю.
«м≥нна ѕδ через тиск розклиненн€ в≥дображаЇ вплив матер≥алу п≥дкладки (ст≥нки). ” загальному випадку вплив ф≥зичних властивостей п≥дкладки на розгл€дуваний процес крапельноњ конденсац≥њ повинен про€вл€тис€ не т≥льки через тиск розклиненн€. ѕульсац≥њ терм≥чного опору конденсату безумовно повинн≥ викликати в≥дпов≥дну реакц≥ю у ст≥нц≥. ƒоповнивши формулюванн€ задач≥ р≥вн€нн€м теплопров≥дност≥ дл€ ст≥нки ≥ в≥дпов≥дними граничними умовами, повинн≥ отримати ще один симплекс под≥бност≥ ат/ар, €кий враховуЇ вплив пульсац≥й температури у ст≥нц≥ на теплов≥ддачу з боку пари.
якщо задати умови однозначност≥ певним чином, то в числа под≥бност≥ додатково можуть в≥йти розм≥ри твердого т≥ла Lmi (≥ = 1, 2...) Ц у тому числ≥ розм≥ри м≥кро проф≥лю поверхн≥ ст≥нки. Ќа сьогодн≥шн≥й день обірунтовано враховувати м≥кро проф≥ль ≥ тим б≥льше знайти залежн≥сть середньоњ теплов≥ддач≥ в≥д розпод≥лу м≥кро неоднор≥дностей Ї недос€жною задачею. –еал≥зац≥€ такого п≥дходу вимагаЇ не т≥льки статистичного опису проф≥лю певними величинами, наприклад середньоквадратичною висотою виступ≥в, але ≥ статистичного п≥дходу до суми досл≥д≥в з р≥зними поверхн€ми, €к≥ характеризуютьс€ р≥зними середньоквадратичними в≥дхиленн€ми в≥д ном≥налу.
—истема безрозм≥рних зм≥нних (13.40) отримана за умови, що поле швидкостей в конденсат≥ обумовлене кап≥л€рними, ≥нерц≥йними силами ≥ силами вТ€зкост≥. —ила т€ж≥нн€ при отриманн≥ безрозм≥рних чисел под≥бност≥ не враховувалас€. “аким чином, вважалос€, що сили т€ж≥нн€ ф≥ксован≥, внасл≥док чого вони винесен≥ з-п≥д знаку функц≥њ. ƒискретн≥сть р≥дкоњ фази спри€Ї прийн€ттю ц≥Їњ умови.
Ќеврахуванн€ сил т€ж≥нн€ Ї недол≥ком системи (13.40). ÷ей недол≥к повинен про€вл€тис€ в умовах зм≥нноњ грав≥тац≥њ дл€ р≥дин з р≥зною густиною ≥ при перех≥дному режим≥ до пл≥вковоњ конденсац≥њ. ƒл€ врахуванн€ сил т€ж≥нн€ до перел≥ку (13.40) можна ввести число √ал≥ле€.
ќчевидно, при зм≥н≥ умов проходженн€ процесу крапельноњ конденсац≥њ список (13.40) необх≥дно поповнювати ≥ ≥ншими необх≥дними безрозм≥рними зм≥нними. “ак, €кщо швидк≥сть пари велика ≥ пара чинить пом≥тну динам≥чну д≥ю на конденсат (зменшуЇтьс€ в≥дривний розм≥р, прискорюЇтьс€ скочуванн€, крапл€ розт≥каЇтьс€ по поверхн≥ та ≥н.), перел≥к необх≥дно доповнити, €к м≥н≥мум, двома зм≥нними, наприклад числами
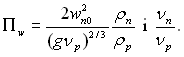
ѕерш≥ досл≥дженн€ крапельноњ конденсац≥њ розпочат≥ в 1930 роках. «а наступн≥ роки накопичений значний, хоч ≥ не вичерпний матер≥ал з питань теплов≥ддач≥ ≥ технолог≥њ п≥дтриманн€ крапельноњ конденсац≥њ на металевих поверхн€х. «деб≥льшого досл≥джувалас€ крапельна конденсац≥€ насиченоњ чи слабо перегр≥тоњ вод€ноњ пари. “иск пари в переважн≥й к≥лькост≥ досл≥д≥в мало в≥др≥зн€вс€ в≥д атмосферного. ћатер≥алом ст≥нки переважно була м≥дь, ≥нколи латунь ≥ сталь. ƒосл≥джувалас€ теплов≥ддача плоскоњ ≥ цил≥ндричноњ вертикальноњ ≥ горизонтальноњ поверхн≥, розм≥ри €коњ невелик≥.
” досл≥дах ≈.√нама конденсац≥€ в≥дбувалас€ на зовн≥шн≥й поверхн≥ вертикальноњ м≥дноњ труби д≥аметром 33 мм ≥ довжиною конденсац≥йноњ д≥л€нки 350 мм. ¬≥дм≥нною особлив≥стю Ї зм≥на тиску вод€ноњ пари в≥д 0,0157 до 0,088 ћѕа, при пом≥рн≥й швидкост≥ теч≥њ.
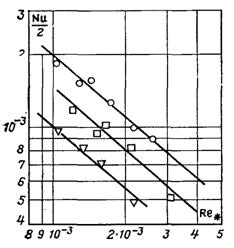
–ис.13.6. «алежн≥сть числа Ќуссельта в≥д –ейнольдса: Щ Ц р = 0,088 ћѕа, ѕк = 4,12Ј10Ц2, Prp = 1,83; £ Ц р = 0,0685 ћѕа, ѕк = 3,55Ј10Ц2, Prp = 1,95; s Ц р = 0,0323 ћѕа, ѕк = 2,14Ј10Ц2, Prp = 2,58
Ќа рис.13.6. наведено опрацюванн€ досл≥дних даних √нама дл€ тиск≥в 0,0323; 0,0985 ≥ 0,088 ћѕа. « граф≥ка видно, що ![]() де показник степен€ дор≥внюЇ приблизно 0,84. ƒосл≥дн≥ дан≥ розшаровуютьс€ по тискам чи по числам Prp ≥ ѕк, оск≥льки ц≥ величини Ї функц≥€ми певноњ температури. «а визначальну прийн€та температура насиченн€.
де показник степен€ дор≥внюЇ приблизно 0,84. ƒосл≥дн≥ дан≥ розшаровуютьс€ по тискам чи по числам Prp ≥ ѕк, оск≥льки ц≥ величини Ї функц≥€ми певноњ температури. «а визначальну прийн€та температура насиченн€.
ƒл€ отриманн€ залежност≥ числа Ќуссельта ≥ ѕк кр≥м даних ≈.√нама використан≥ результати досл≥д≥в ≥нших автор≥в.
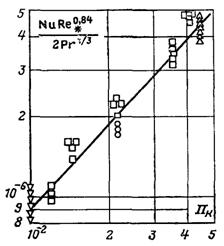
–ис.13.7. ¬и€вленн€ впливу кап≥л€рних сил на процес крапельноњ конденсац≥њ пари
Ќа рис.13.7 досл≥дн≥ дан≥ наведен≥ у вигл€д≥ залежност≥
![]()
з €коњ видно, що теплов≥ддача суттЇво залежить в≥д числа ѕк, показник степен€ при €кому дор≥внюЇ приблизно 1,16. “аким чином, кап≥л€рн≥ сили суттЇво впливають на процес.
ƒосл≥дн≥ дан≥ наведен≥ на рис.13.7 в≥дпов≥дають числам –ейнольдса меншим 3,3Ј10Ц3, оск≥льки при значенн€х р≥вних наведеному числу, залежн≥сть Ќуссельта в≥д –ейнольдса зм≥нюЇтьс€. ѕро це св≥дчить зведений граф≥к наведений на рис.13.8, на €кому наведен≥ результати експеримент≥в ≈.Ўм≥дта, —.—. утателадзе, “.ћ≥цушина, ¬.ѕ.≤саченка ≥ ј.ѕ.—олодова. ƒосл≥дженн€ двох останн≥х автор≥в характеризуютьс€ наступними умовами: поверхн€ теплообм≥ну Ц вертикальна м≥дна пластина 150ќ30ќ20 мм; г≥дрофоб≥затор Ц октадец≥лселеноц≥ан≥д розведений до 1%; тиск насиченоњ пари незначно перевищував атмосферний тиск.
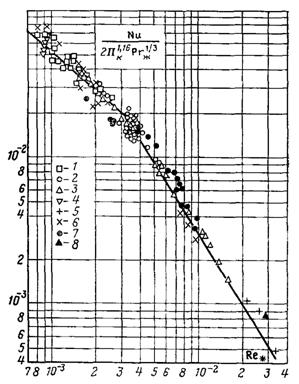
–ис.13.8. “еплообм≥н при крапельн≥й конденсац≥њ пари:£ Ц √нам; Щ Ц Ќегль; r Ц Ў≥ ≥ ‘рейз; s Ц Ћапшин ≥ онфедератов; ∆ Ц Ўм≥дт; ќ Ц утателадзе; Ш Ц ≤саченко ≥ —олодов; p Ц ћ≥цуш≥на
«алежн≥сть наведену на рис.13.8 можна описати наступними р≥вн€нн€ми:
при Re* = 8Ј10Ц4Е3,3Ј10Ц3
![]() (13.44)
(13.44)
при Re* = 3,3Ј10Ц3Е3,4Ј10Ц2
![]() (13.45)
(13.45)
«наченн€ числа под≥бност≥ ѕк в досл≥дних даних зм≥нювалос€ в≥д 0,98Ј10Ц2 до 4,5Ј10Ц2; число ѕрандтл€ зм≥нювалос€ в≥д 1,75 до 3,65.
« формул (13.44) ≥ (13.45) сл≥дуЇ, що
при Re* < 3,3Ј10Ц3
![]() (13.46)
(13.46)
при Re* > 3,3Ј10Ц3
![]() (13.47)
(13.47)
“аким чином при Re* = 3,3Ј10Ц3 позитивна залежн≥сть ![]() переходить в негативну. ” той же час залежн≥сть теплового потоку в≥д температури завжди позитивна. ƒодатну залежн≥сть функц≥њ
переходить в негативну. ” той же час залежн≥сть теплового потоку в≥д температури завжди позитивна. ƒодатну залежн≥сть функц≥њ ![]() можна по€снити зб≥льшенн€м к≥лькост≥ центр≥в конденсац≥њ з≥ зростанн€м температурного напору. ѕри цьому утворенн€ новоњ фази, ≥ €к насл≥док, зб≥льшенн€ њњ к≥лькост≥, стаЇ б≥льш ймов≥рною. «б≥льшенн€ к≥лькост≥ фази на поверхн≥ теплообм≥ну у свою чергу веде до зменшенн€ поверхневих сил, зб≥льшуЇтьс€ час перем≥щенн€ р≥дких частинок по поверхн≥ ≥ час њх видаленн€. Ўвидк≥сть видаленн€ р≥дкоњ фази починаЇ все б≥льше в≥дставати в≥д швидкост≥ њњ утворенн€, що у п≥дсумку призводить до в≥дТЇмноњ залежност≥.
можна по€снити зб≥льшенн€м к≥лькост≥ центр≥в конденсац≥њ з≥ зростанн€м температурного напору. ѕри цьому утворенн€ новоњ фази, ≥ €к насл≥док, зб≥льшенн€ њњ к≥лькост≥, стаЇ б≥льш ймов≥рною. «б≥льшенн€ к≥лькост≥ фази на поверхн≥ теплообм≥ну у свою чергу веде до зменшенн€ поверхневих сил, зб≥льшуЇтьс€ час перем≥щенн€ р≥дких частинок по поверхн≥ ≥ час њх видаленн€. Ўвидк≥сть видаленн€ р≥дкоњ фази починаЇ все б≥льше в≥дставати в≥д швидкост≥ њњ утворенн€, що у п≥дсумку призводить до в≥дТЇмноњ залежност≥.
як сл≥дуЇ з формул (13.44) ≥ (13.45), дл€ розрахунку коеф≥ц≥Їнта теплов≥ддач≥ вод€ноњ пари достатньо знати температуру насиченн€ ≥ температурний нап≥р. омплекси величин, €к≥ залежать в≥д температури насиченн€, можна представити у вигл€д≥ функц≥њ температури чи тиску насиченн€. “од≥ р≥вн€нн€ (13.44) ≥ (13.45) можна в≥дпов≥дно записати наступним чином:
![]() (13.48)
(13.48)
≥
![]() (13.49)
(13.49)
‘ункц≥њ F1(Tн) ≥ F2(Tн) дл€ води апроксимован≥ степеневими залежност€ми
![]()
≥
![]()
де a, b, n ≥ т Ц стал≥ величини.
¬насл≥док п≥дстановки останн≥х вираз≥в в (13.48) ≥ в (13.49) отриман≥ наступн≥ прост≥ формули:
при Re* = 8Ј10Ц4Е3,3Ј10Ц3
![]() (13.50) ≥ (13.51)
(13.50) ≥ (13.51)
при Re* = 3,3Ј10Ц3Е3,4Ј10Ц2
![]() (13.52) ≥ (13.53)
(13.52) ≥ (13.53)
” формулах (13.50)...(13.53) температура насиченн€ tн п≥дставл€Їтьс€ в градусах ÷ельс≥€, тиск насиченоњ пари рн Ц у барах. ¬еличина Jн представл€Ї собою температурний нап≥р, р≥вний р≥зниц≥ “н Ц “(с. ѕри цьому середн≥й коеф≥ц≥Їнт теплов≥ддач≥ виражений у ¬т/(м2Ј ). Ќазван≥ формули справедлив≥ при тих же умовах, що ≥ р≥вн€нн€ (13.44) ≥ (13.45). √раф≥ки побудован≥ на п≥дстав≥ формул (13.50)...(13.53) наведен≥ на рис.13.9 ≥ 13.10.
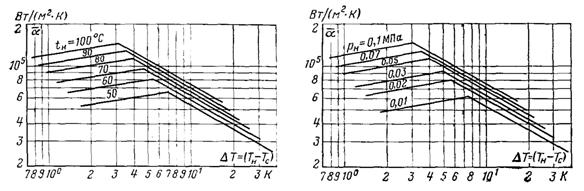
↑–ис.13.9. «алежн≥сть коеф≥ц≥Їнта теплов≥ддач≥ в≥д Δ“ ≥ “н
–ис.13.10. «алежн≥сть коеф≥ц≥Їнта теплов≥ддач≥ в≥д Δ“ ≥ рн ↑
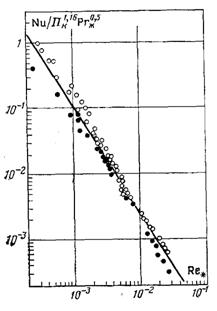
–ис.13.11. “еплов≥ддача при крапельн≥й конденсац≥њ вод€ноњ пари (Ш) ≥ пари етиленгл≥колю (Щ) за даними ѕетерсона ≥ ”естуотера
ѕетерсон ≥ ”естуотер опрацювали отриман≥ ними експериментальн≥ дан≥ виконан≥ при крапельн≥й конденсац≥њ пари води ≥ етиленгл≥колю. Ќими отримана т≥льки в≥дТЇмна г≥лка залежност≥ (рис.13.11). «адов≥льна апроксимац≥€ ними дос€гнута при наступному запис≥ р≥вн€нн€ (13.45):
![]() (13.54)
(13.54)
при цьому д≥апазон зм≥нних величин становив ѕк = 7,8Ј10Ц4...2,65Ј10Ц2; Prp = 1,75...23,6. ѕри пор≥вн€нн≥ формули (13.54) з (13.45) можна побачити, що в перш≥й трохи скоректован≥ показники степен€ при –ейнольд≥ (Ц1,63 зам≥сть Ц1,57), а при числ≥ ѕрандтл€ прийн€то 0,5 зам≥сть 1/3.
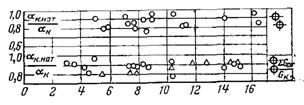
–ис.13.12. ¬плив нат≥канн€ конденсату на теплов≥ддачу при крапельн≥й конденсац≥њ
Ќа рис.13.12 наведен≥ досл≥дн≥ дан≥ про вплив нат≥канн€ на теплов≥ддачу дл€ коридорноњ ≥ шаховоњ схем розм≥щенн€ трубок (в≥дпов≥дно нульове зм≥щенн€ ≥ зм≥щенн€ на величину рад≥уса в горизонтальн≥й площин≥). як сл≥дуЇ з рисунка, зменшенн€ теплов≥ддач≥ внасл≥док нат≥канн€ дос€гаЇ приблизно 15% €к при коридорному, так ≥ при шаховому розм≥щенн≥ трубок. “аким чином, €к при пл≥вков≥й, так ≥ при крапельн≥й конденсац≥њ пари на горизонтальн≥й труб≥ вплив конденсату, що скочуЇтьс€ зверху, невеликий.
рапельна конденсац≥€ вод€ноњ пари у пор≥вн€нн≥ з пл≥вковою даЇ б≥льш висок≥ коеф≥ц≥Їнти теплов≥ддач≥. ÷е дозвол€Ї вважати њњ перспективним процесом дл€ ≥нтенсиф≥кац≥њ теплообм≥ну.
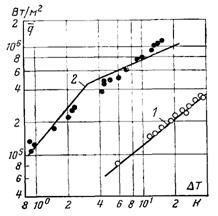
а) б)
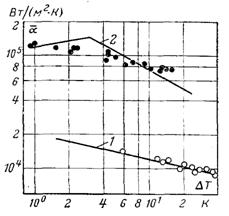
–ис.13.13. ѕор≥вн€нн€ коеф≥ц≥Їнт≥в теплов≥ддач≥ при пл≥вков≥й (1) ≥ крапельн≥й (2) конденсац≥њ вод€ноњ пари на вертикальн≥й пластин≥: а Ц залежн≥сть середньоњ ≥нтенсивност≥ теплового потоку в≥д р≥зниц≥ температур; б Ц залежн≥сть середнього коеф≥ц≥Їнта теплов≥ддач≥ в≥д р≥зниц≥ температур
Ќа рис.13.13 наведен≥ досл≥дн≥ дан≥, отриман≥ на м≥дн≥й вертикальн≥й пластин≥ висотою 150 мм. ƒосл≥джувалис€ пластини без покритт€ ≥ з ~3 мм покритт€м фторопластом-4. ¬≥дпов≥дно при цьому мала м≥сце пл≥вкова чи крапельна конденсац≥€ насиченоњ вод€ноњ пари приблизно при атмосферному тиску. як св≥дчать граф≥ки, крапельна конденсац≥€ при Δ“ = idem веде до суттЇвого зб≥льшенн€ теплообм≥ну.
13.7. “еплообм≥н при конденсац≥њ рухомоњ пари
–ан≥ше розгл€нутий теплообм≥н при невеликих швидкост€х пари, коли його динам≥чною д≥Їю на конденсат можна нехтувати. —пр€мований рух пари може привести до направленого руху конденсату. ѕроцес при цьому набуваЇ певноњ упор€дкованост≥ ≥ залежить в≥д швидкост≥ пари ≥ ф≥зичних властивостей.
якщо пара чиста, тобто в≥дсутн≥ неконденсован≥ дом≥шки, швидк≥сть пари впливаЇ т≥льки на терм≥чний оп≥р конденсату. ” подальшому у цьому параграф≥ будемо розгл€дати чисту пару.
” л≥тератур≥ майже в≥дсутн≥ досл≥дженн€ впливу швидкост≥ пари на теплообм≥н при краплинн≥й конденсац≥њ. Ќайб≥льш правильно, з методичноњ точки зору, побудован≥ досл≥дженн€ ‘.Ў≥ ≥ Ќ. ейза. «а њх даними були розрахован≥ теплообм≥нн≥ характеристики дл€ д≥л€нок довжиною 117, 234, 351, 468 ≥ 585 мм (в≥дл≥к в≥д вх≥дного перер≥зу). —ередн≥ значенн€ qc,Jн ≥ α зм≥нювалис€ в≥дпов≥дно в наступних межах: 1,16Ј(2,25...7,92)Ј105, ¬т/м2; 0,75...8,75, ∞— ≥ 1,16Ј(75...365)Ј103 ¬т/(м2Ј ). —ередн€ у перер≥з≥ розрахункова швидк≥сть пари на вход≥ у досл≥дний конденсатор становила приблизно в≥д 4,5 до 13,5 м/с. ¬≥дпов≥дно до цих значень швидкост≥ число –ейнольдса дл€ пари Reп0 = wn0h/νn зм≥нювалос€ в д≥апазон≥ в≥д 5700 до 16800 (h Ц висота щ≥лини, wn0 Ц швидк≥сть пари на вход≥). ћаксимальне значенн€ числа –ейнольдса дл€ р≥дини Reр0 = qc0ℓ0 /rμp приблизно становило 586 (ℓ0 Ц повна довжина пластини).
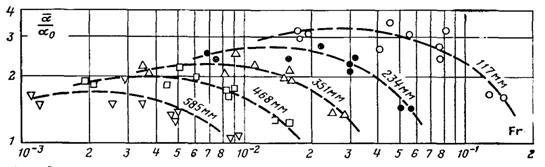
–ис.13.14. «алежн≥сть в≥дносного коеф≥ц≥Їнта теплов≥ддач≥ в≥д числа ‘руда при ℓ, мм: Щ Ц 117; Ш Ц 234; rЦ 351; £ Ц 468; s Ц 585
оеф≥ц≥Їнт теплов≥ддач≥ у пор≥вн€нн≥ з≥ значенн€ми, €к≥ визначаютьс€ при тих же J(н ≥ “н за формулами (13.44) ≥ (13.45), зб≥льшивс€ в 1,05...3,52 рази (рис.13.14). Ќа цьому рисунку в≥дносн≥ середн≥ коеф≥ц≥Їнти теплов≥ддач≥ наведен≥ у залежност≥ в≥д числа ‘руда Fr = 2ρnw 2n/ρpgℓ, де wn Ц середньоарифметична швидк≥сть пари на розгл€дуван≥й д≥л€нц≥; ℓ Ц довжина осередненн€, €ка в≥драховуЇтьс€ в≥д вх≥дноњ кромки. Ќа рис.13.14 α0 Ц коеф≥ц≥Їнт теплов≥ддач≥, €кий розраховуЇтьс€ за р≥вн€нн€ми (13.44) ≥ (13.45). ‘≥зичн≥ параметри вод€ноњ пари вибиралис€ за “н = 372,3 .
ѕри такому опрацюванн≥ експериментального матер≥алу неможна отримати однозначну залежн≥сть. јнал≥з даних показуЇ, що в≥дношенн€ J0 тим менше, чим б≥льший температурний нап≥р. ѕунктирн≥ л≥н≥њ, €к≥ в≥дпов≥дають певним довжинам поверхн≥ теплообм≥ну, т≥льки умовно поЇднують досл≥дн≥ точки. ѕри значн≥й зм≥н≥ J(н розс≥в досл≥дних точок в≥дносно пунктирноњ л≥н≥њ може бути досить великим ≥ ч≥ткий розпод≥л за довжинами ℓ зникаЇ.
ѕроцес зм≥нюЇтьс€ по висот≥ пластини, але ц≥ зм≥ни можуть бути врахованими за допомогою J(н ≥ wп (при повн≥й конденсац≥њ Ц т≥льки через J(н), без введенн€ в €вному вигл€д≥ л≥н≥йного розм≥ру. «алежн≥сть теплов≥ддач≥ в≥д швидкост≥ пари показана на рис.13.15, де узагальненн≥ досл≥дн≥ дан≥ наведен≥ на рис.13.14, отриман≥ при Re* < 3,3Ј10Ц3. ѕри узагальненн≥ прийн€то, що
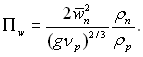
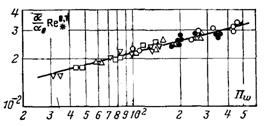
–ис.13.15. «алежн≥сть теплов≥ддач≥ в≥д числа ѕw. ѕозначенн€ точок т≥ ж, що ≥ на рис.13.14
як видно з рис.13.15, вплив швидкост≥ пари досить великий: α| ~ wn 0,5
ѕор≥вн€но з пл≥вковою конденсац≥Їю швидк≥сть пари при крапельн≥й конденсац≥њ б≥льш суттЇво впливаЇ на теплов≥ддачу. ÷ей вплив про€вл€Їтьс€ в тому, що теплов≥ддача починаЇ суттЇво залежати в≥д швидкост≥ вже при пор≥вн€нно невеликих значенн€х останньоњ. як в≥дм≥чалос€ ран≥ше, швидк≥сть пари на вход≥ зм≥нювалас€ в д≥апазон≥ 4,5...13,5 м/с. ѕри пл≥вков≥й конденсац≥њ вод€ноњ пари приблизно в тих же умовах швидк≥сть пари майже не впливала на ≥нтенсивн≥сть процесу.
¬≥дм≥чений результат не Ї неспод≥ваним. Ќа€вн≥сть на поверхн≥ ст≥нки крапель, €к≥ безперервно зростають, скочуютьс€ вниз ≥ зливаютьс€ м≥ж собою, призводить до складноњ модел≥ поточноњ шорсткост≥. —ередн≥ параметри такоњ шорсткост≥ можна визначити, €кщо в≥дома функц≥€ розпод≥лу крапель за розм≥рами. ѕри цьому параметри шорсткост≥ повинн≥ бути функц≥Їю досл≥джуваного процесу. ≤нтенсивн≥сть теплообм≥ну ≥ опори залежать в≥д висоти елемент≥в шорсткост≥, њх форми ≥ концентрац≥њ. «а цих умов точно оц≥нити можлив≥ коеф≥ц≥Їнти г≥дравл≥чного опору при обт≥канн≥ парою поверхн≥, €ка спов≥льнюЇ св≥й рух, стаЇ малоймов≥рним. ћожна виконати т≥льки грубу оц≥нку величини опору.
якщо в≥дривний рад≥ус крапель оц≥нити в 1 мм, то в першому наближенн≥ при Re = 104 коеф≥ц≥Їнт г≥дравл≥чного опору зб≥льшуЇтьс€ в 1,5 рази. Ќе дивл€чись на умовн≥сть такоњ оц≥нки, сам факт зб≥льшенн€ опору на границ≥ фаз виходить повн≥стю обірунтованим. «в≥дки, €к насл≥док, вит≥каЇ ≥нтенсиф≥кац≥€ теплообм≥ну.
ћожна в≥дм≥тити де€к≥ особливост≥ впливу швидкост≥ пари у випадку крапельноњ конденсац≥њ. ѕринципова сторона впливу швидкост≥ при цьому €к у випадку крапельноњ, так ≥ пл≥вковоњ конденсац≥њ одна ≥ та ж Ц п≥двищенн€ швидкост≥ пари приводить до б≥льш швидкого видаленн€ з поверхн≥ ст≥нки конденсату, що утворивс€, чим зменшуЇ терм≥чний оп≥р.
” випадку крапельноњ конденсац≥њ зб≥льшенн€ швидкост≥ пари повинно привести до зменшенн€ в≥дривного розм≥ру крапл≥, ≥ до зменшенн€ пром≥жку часу, необх≥дного дл€ росту крапл≥. «≥ зб≥льшенн€м швидкост≥ пари повинен зменшуватис€ час скочуванн€.
” той же час утворенн€ великоњ к≥лькост≥ конденсату, звТ€зане впливом швидкост≥ на ≥нтенсиф≥кац≥ю процесу, що може привести до п≥дсиленн€ залежност≥ в≥д температурного напору у зв'€зку ≥з заливанн€м поверхн≥ теплообм≥ну. якщо при цьому виконуЇтьс€ умова F[ℓ(Jн)] = F(Jн), то процес буде ≥нвар≥антним в≥дносно л≥н≥йного розм≥ру.
як сл≥дуЇ з рис.13.15, теплов≥ддача ≥нвар≥антна в≥дносно повздовжнього л≥н≥йного розм≥ру поверхн≥ теплообм≥ну. ¬плив л≥н≥йного розм≥ру про€вл€Їтьс€ через температурний нап≥р. Ѕезумовно, цей вив≥д справедливий стосовно досл≥дних даних ≥ внасл≥док використанн€ цього обмеженн€.
ƒосл≥дн≥ дан≥ отриман≥ при “н = const ≥ в основному при температурних напорах J(н < 3,1 , що при атмосферному тиску в≥дпов≥даЇ дл€ нерухомоњ пари додатн≥й залежност≥ α(Jн ). ѕри J(н > 3,1 досл≥дженн€ обмежен≥ двома сер≥€ми (дес€тьма експериментальними точками).
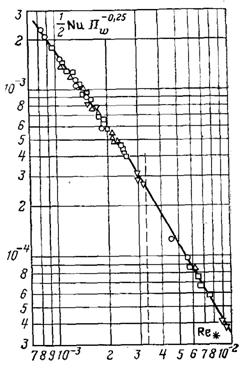
–ис.13.16. «алежн≥сть теплов≥ддач≥ при конденсац≥њ рухомоњ пари в≥д числа –ейнольдса. ѕозначенн€ точок т≥ ж, що ≥ на рис.13.14
¬иконаних досл≥джень недостатньо дл€ отриманн€ обірунтованоњ залежност≥ теплов≥д-дач≥ в≥д швидкост≥ пари при Re* > 3,3Ј10Ц3. ” першому наближенн≥ отриману залежн≥сть α|/α0 в≥д ѕw можна розповсюдити на область Re* > 3,3Ј10Ц3. ќпрацьован≥ таким чином дан≥ наведено на рис.13.16. ƒе
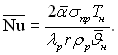
як сл≥дуЇ з граф≥ка при Re* > 3,3Ј10Ц3 залежн≥сть теплов≥ддач≥ в≥д Re* зм≥нюЇтьс€ Ц в≥дТЇмний вплив температурного напору п≥дсилюЇтьс€:
при Re* = 8Ј10Ц4Е3,3Ј10Ц3
![]() (13.55)
(13.55)
при Re* = 3,3Ј10Ц3Е9Ј10Ц3
![]() (13.56)
(13.56)
–≥вн€нн€ (13.55) ≥ (13.56) в≥дпов≥дають в≥дпов≥дно значенн€м ѕw = 30...450 ≥ ѕw = 110...1290.
« формул (13.55) ≥ (13.56) виходить, що коеф≥ц≥Їнт теплов≥ддач≥ зменшуЇтьс€ при зб≥льшенн≥ температурного напору.
“аким чином, при на€вност≥ суттЇвоњ тангенц≥альноњ швидкост≥ пари зм≥на додатного характеру залежност≥ ![]() на в≥дТЇмний в≥дбуваЇтьс€ при значно менших температурних напорах. якщо врахувати ту обставину, що найменший температурний нап≥р, €кий мав м≥сце в розгл€дуваних експериментах, становив приблизно 0,75 , то можна сказати, що при значних швидкост€х пари буде реал≥зуватис€ в≥дТЇмна г≥лка залежност≥
α(Jн ).
на в≥дТЇмний в≥дбуваЇтьс€ при значно менших температурних напорах. якщо врахувати ту обставину, що найменший температурний нап≥р, €кий мав м≥сце в розгл€дуваних експериментах, становив приблизно 0,75 , то можна сказати, що при значних швидкост€х пари буде реал≥зуватис€ в≥дТЇмна г≥лка залежност≥
α(Jн ).
13.8. онденсац≥€ пари з паро-газовоњ сум≥ш≥
” зв'€зку з тим, що при крапельн≥й конденсац≥њ терм≥чний оп≥р конденсату малий, то зб≥льшуЇтьс€ вплив дифуз≥йного опору. ѕри одн≥й ≥ т≥й же концентрац≥њ неконденсованих газ≥в ≥ ≥нших р≥вних умовах у випадку крапельноњ конденсац≥њ може мати м≥сце б≥льш сильний про€в сумарноњ характеристики теплообм≥ну, н≥ж при пл≥вков≥й.
ѕри пл≥вков≥й конденсац≥њ пари завжди виникаЇ конвекц≥€. Ўвидк≥сть парогазовоњ сум≥ш≥ може впливати €к на терм≥чний оп≥р конденсату, так ≥ на дифуз≥йний оп≥р. ќстанн≥й оп≥р повинен суттЇво залежати в≥д швидкост≥, при цьому у загальному випадку залежн≥сть дифуз≥йного опору в≥д швидкост≥ може бути р≥зною дл€ пл≥вковоњ ≥ крапельноњ конденсац≥њ, тому що конф≥гурац≥€ сконденсованих утворень також р≥зна.
ѕоверхн€, €ка покрита крапл€ми, може розгл€датис€, €к шорстка. ≈фективна величина терт€ при цьому може мати б≥льш висок≥ значенн€ ≥ тангенц≥альний пот≥к сум≥ш≥ може суттЇво впливати €к на терм≥чний, так ≥ на дифуз≥йний оп≥р конденсату. ƒан≥ про впив швидкост≥ на дифуз≥йний терм≥чний оп≥р обмежен≥. –€д публ≥кац≥й навод€тьс€ так, що вид≥лити з розмањтт€ фактор≥в вплив швидкост≥ практично неможливо.
” подальшому розгл€немо теплообм≥н при пор≥вн€нно невеликих швидкост€х паропов≥тр€ноњ сум≥ш≥ п≥д час конденсац≥њ, що в≥дбуваЇтьс€ на горизонтальн≥й м≥дн≥й трубц≥ д≥аметром 12,6 мм, розм≥щен≥й в достатньо великому обТЇм≥ пари. ¬х≥д пари зверху.
¬ одн≥й сер≥њ досл≥д≥в трубка була оточена двома концентричними прилеглими одна до ≥ншоњ латунними дрот€ними с≥тками. ¬нутр≥шн€ с≥тка мала отвори по 200 мкм, зовн≥шн€ Ц по 50 мкм. ≈кран мав д≥аметр 102 мм ≥ з торц≥в закривавс€ глухими кришками. як показали розрахунки, у цих досл≥дженн€х повинен реал≥зуватис€ рад≥альний п≥дв≥д пари до поверхн≥ конденсац≥њ. рапельна конденсац≥€ дос€галас€ нанесенн€м на трубку октадец≥лселенц≥ан≥ду 1%-ного розчину у чотири хлористому вуглец≥.
ƒл€ визначенн€ дифуз≥йного опору необх≥дно знати температуру поверхн≥ конденсату. ÷€ температура розраховувалас€ за р≥вн€нн€м (13.50), де “н=“п.пов, оск≥льки величина Re*, розрахована по “п.пов Ц “(с, була меншою за 3,3Ј10Ц3.
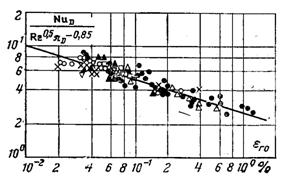
–ис.13.17. ћасов≥ддача у досл≥дах без с≥тки при “п0, : £ Ц 328; r Ц 333; s Ц 338; p Ц 343; ќ Ц 353; Щ Ц 363; Ш Ц пл≥вкова конденсац≥€
ћожна вважати, що при несиметричн≥й подач≥ пари, €ке мало м≥сце у досл≥дах без с≥тки, на трубц≥ утворюЇтьс€ пограничний шар. „исла Re = q(cd/rμn мали у цих досл≥дах величину 24,6...168, тобто були достатньо велик≥. ¬≥льн≥ токи при цьому сп≥впадали з напр€мком руху пари, обумовленим процесом конденсац≥њ.
¬раховуючи назван≥ обставини, опрацюванн€ досл≥дних даних виконано у вигл€д≥ залежност≥ (рис.13.17):
![]()
„исло –ейнольдса в даному випадку не може бути заданим наперед ≥ Ї функц≥Їю тих же зм≥нних, в≥д €ких залежить ![]() тобто комплекс
тобто комплекс ![]() сл≥д вважати окремою зм≥нною величиною. „исло PrD п≥д час досл≥д≥в практично не зм≥нювалос€.
сл≥д вважати окремою зм≥нною величиною. „исло PrD п≥д час досл≥д≥в практично не зм≥нювалос€.
«г≥дно рис.13.17 середн≥й коеф≥ц≥Їнт масов≥ддач≥ можна подати в наступному вид≥:
![]() (13.57)
(13.57)
чи враховуючи, що
![]()
отримаЇмо
![]() (13.58)
(13.58)
” цих р≥вн€нн€х πD = (рп0 Ц рп.пов)/р = 0,052...0,746, масовий вм≥ст пов≥тр€ на вход≥ εг0 = 2Ј10Ц4...5Ј10Ц3. ¬изначальн≥ розм≥р ≥ температура Ц д≥аметр труби ≥ температура сум≥ш≥ на вход≥ “п0. Ќа рис.13.17 ≥ в р≥вн€нн€х (13.57) ≥ (13.58) εг0 виражаЇтьс€ у в≥дсотках.
ѕрактично аналог≥чн≥ результати отриман≥ дл€ випадку подач≥ парогазовоњ сум≥ш≥ знизу.
¬арто в≥дм≥тити, що на рис.13.17 наведен≥ дан≥, отриман≥ при крапельн≥й ≥ пл≥вков≥й конденсац≥њ. “аким чином, в умовах експерименту дифуз≥йний терм≥чний оп≥р практично не залежить в≥д характеру конденсац≥њ. ¬насл≥док цього вбачаЇтьс€ можлив≥сть використанн€ дл€ розрахунку крапельноњ конденсац≥њ де€ких результат≥в, отриманих ран≥ше дл€ дифуз≥йного опору при пл≥вков≥й конденсац≥њ. јле цей висновок не варто переносити на б≥льш висок≥ числа –ейнольдса.
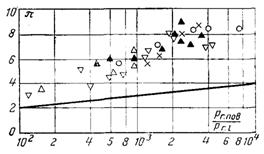
–ис.13.18. ћасов≥ддача в досл≥дах з с≥ткою [крива в≥дпов≥даЇ розрахунку за (12.15)]. ѕозначенн€ див. рис.13.17.
ƒосл≥ди з с≥ткою, в €ких практично зд≥йснювавс€ рад≥альний п≥дв≥д пари, показують приблизно в 1,5...2 рази нижчу масов≥ддачу, н≥ж це сл≥дуЇ з формули (13.57), але б≥льш високу в пор≥вн€нн≥ з формулою (12.15) дл€ рад≥альноњ теч≥њ пари (рис.13.18). ¬≥дхиленн€ в≥д формули (12.15) по€снюЇтьс€ впливом на теплообм≥н в≥льноњ конвекц≥њ, що ч≥тко видно з рис.13.18, де наведен≥ т≥ ж дан≥. “ут β0 визначаЇтьс€ за р≥вн€нн€м (12.15); Ar = (gd3/νп2)(ρ Ц ρ0)/ρ0; ρ ≥ ρ0 Ц в≥дпов≥дно густина сум≥ш≥ на поверхн≥ конденсату ≥ на в≥дстан≥ в≥д нењ (на с≥тц≥).
јпроксимац≥€ кривоњ на рис.13.19 в≥дпов≥даЇ р≥вн€нню (12.17):
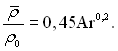
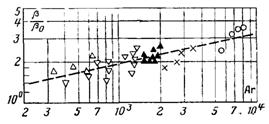
–ис.13.19. «алежн≥сть в≥дносного коеф≥ц≥Їнта масов≥ддач≥ в≥д числа јрх≥меда. ѕозначенн€ т≥ сам≥, що ≥ на рис.3.17
« приведених даних виходить, що при пом≥рних швидкост€х парогазового потоку теплов≥ддача невелика. Ќаприклад у досл≥дах без с≥тки при εг0 = 1% результуючий коеф≥ц≥Їнт теплов≥ддач≥ αсм приблизно в 5 раз≥в менший, н≥ж при конденсац≥њ чистоњ вод€ноњ пари.