Розділ 15. ТЕПЛООБМІН ПРИ КОНДЕНСАЦІЇ ПАРИ НА ДИСПЕРГОВАНОМУ СТРУМЕНІ РІДИНИ

15.1. Швидкість прогрівання краплі

При витіканні рідини в режимі розпилювання (великі швидкості, застосування спеціальних форсунок) ділянка, на якій зберігається суцільна течія в ядрі струменя, практично відсутня чи настільки мала, що її наявність не відбивається на характеристиках прогрівання струменя. Струмінь розпадається на велику кількість крапель, розміри яких суттєво менші вихідного діаметра сопла. Сукупність дрібних крапель утворює певний статистичний розподіл за розмірами, характеристики яких різні для різних видів форсунок, роду рідини та інше.

Конденсація пари на розпиленому струмені притягує увагу із-за високої інтенсивності цього процесу, викликаній різким збільшенням поверхні контакту з парою і можливим зменшенням термічного опору переносу теплоти. При конденсації чистої пари такими опорами є опір рідкої фази і міжфазний опір.

Процес конденсації можна представити таким, що складається з двох стадій: нерівноважної і квазірівноважної. За час нерівноважної стадії відбувається миттєвий нагрів поверхні холодної краплі від початкової температури до температури фазового переходу. На цій стадії швидкість процесу лімітується фазовим опором.

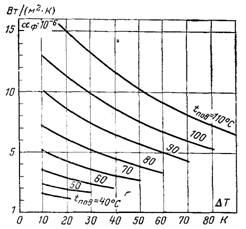
Рис.15.1. Залежність величини, зворотної міжфазному термічному опору, від Т_пов і Т_н – Т_пов; вода і водяна пара, f = 1

На рис.15.1 наведені результати розрахунку α_ф по формулі (8.52) для різних значень температури поверхні Т_пов і різниці    Т_н – Т_пов. Міжфазний термічний опір 1/α_ф  становить величину порядку 10^–7 (м²·К)/Вт, що набагато менше термічного опору більшості крапель, які утворюються при диспергуванні струменю, якщо вважати, що значення цього опору має порядок R/λ_p.

Після закінчення нерівноважної стадії швидкість процесу конденсації насиченої пари обмежена термічним опором краплі. На поверхні краплі відбувається квазірівноважна конденсація, інтенсивність якої зменшується по мірі прогрівання краплі. Радіус краплі збільшується за рахунок приєднаної маси.

При збільшенні радіуса на dR до краплі підводиться теплота (вважаємо, що густина теплового потоку q_гр не змінюється по поверхні)

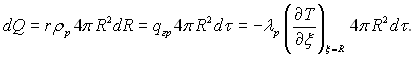(15.1)

Звідки слідує, що

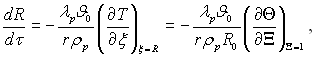(15.2)

де J₀ = Т_н –Т₀; Т₀, R₀ – початкова температура і радіус краплі; Θ = J/J₀; Ξ = ξ/R; ξ – поточний радіус краплі. У першому наближенні величину (дΘ/дΞ)_Ξ=1  можна визначити, розв’язуючи диференціальне рівняння теплопровідності для випадку нагріву рідкої кулі при заданій температурі на поверхні:

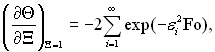(15.3)

де ε_і = іπ; Fo = а_рτ/R². З рівнянь (15.2) і (15.3) виходить, що

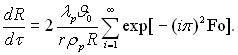(15.4)

Ряд швидко сходиться. При Fo > 0,25 зазвичай задовольняється урахуванням тільки першого члена (і = 1). Тоді

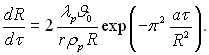(15.5)

Виконаний розрахунок ΔR/Δτ   по формулі (15.4) для випадку конденсації водяної пари на краплях води при Т_н = 373 К з початковим недогрівом Т_н – Т₀ = = 10...80 К, R₀ = 0,1...1,0 мм. Сума ряду у формулі (15.4) розраховувалася з точністю до 0,05%. Вважалося, що радіус краплі, яка росте, задовольняє рівняння теплового балансу

де Т – середньомасова температура зростаючої краплі; с_рр – ізобарна теплоємність рідини.

Введемо безрозмірні змінні

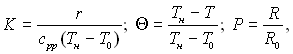
тоді рівняння теплового балансу можна записати в наступному виді:

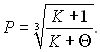(15.6)

У початковий момент часу недогрів Θ = 1 і Р = Р₀ = 1; при Т → Т_н маємо  Θ → 0 і кінцевий радіус краплі Р_к = R_к/R₀ визначається рівнянням

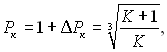(15.7)

де ΔР_к =(R_к – R₀)/R₀. Якщо К >> 1, з останнього рівняння слідує, що Р_к ≈ Р₀ = 1.

Виходячи з викладеного, табульовану функцію, яка апроксимує цифрові значення R (R₀, τ), необхідно шукати в наступному виді:

де ψ(Fo) повинна змінюватися від 0 до 1. Табличні значення R (R₀, τ) описуються формулою:

(15.8)

де Fo = а_рτ/R₀².

Безрозмірна швидкість росту краплі:

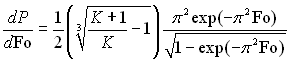(15.9)

чи

(15.10)

Під час конденсаційного росту радіусу крапля збільшується незначно. Наприклад, для випадку конденсації водяної пари на краплі води при Т_н = 373 К і Т_н – Т₀ = 40 К радіус збільшується приблизно на 2,5%.

Експериментальна перевірка формули (15.8) за допомогою швидкісної кінозйомки показала, що збільшення розміру краплі води з початковим діаметром 1,76 мм, що падає в зустрічному потоці водяної пари, надійно погоджується з цією формулою.

Під час руху з відносно великою швидкістю може виникати деформація краплі. Деформацію можна характеризувати відношенням

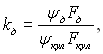
де ψ, F – відповідно коефіцієнт аеродинамічного опору і мідельовий переріз деформованої і кулястої крапель. Величина k_д майже не залежить від Re і визначається рівнянням

де We = 2ρ_гw²R/σ; ρ_г – густина газового середовища, в якому рухається крапля.

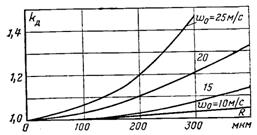
Рис.15.2. Залежність коефіцієнта деформації краплі від її розміру і швидкості

Залежність k_д від w і R наведена на рис.15.2. Тільки крупні краплі при відносно великих швидкостях відчутно деформуються. Кількість таких крапель у диспергованому струмені, який витікає з відцентрової форсунки, мала. Деформація неминуче приводить до руху рідини всередині краплі. Рух може виникнути і в гіпотетичній кулястій краплі, якщо розподіл сил, прикладених до її поверхні, неоднорідний. Конвекція у краплі вивчена недостатньо. Певні висновки про інтенсивність переносу теплоти в краплі можна зробити на підставі аналогії з переносом маси.

Отримане числове рішення рівняння руху для ламінарного омивання недеформованої рідинної кулі стаціонарним потоком суцільного середовища з іншими властивостями. Лінії току в краплі розраховані при 0 0 ≤ Re ≤ 80 і             0 ≤ μ_к/μ_с ≤ ∞, де μ_к і μ_с – коефіцієнти динамічної в’язкості рідкої краплі і оточуючого середовища. На основі цього виконані розрахунки середньої концентрації домішок у краплі як функцію часу. При μ̃ = μ_к/μ_с > 10, що практично відповідає умові μ̃ → ∞, конвекція в краплі згасає і швидкість переносу маси наближається до величини, яка визначається інтенсивністю молекулярної дифузії. В умовах конденсації водяної пари на краплях води часто виконуються умови, які відповідають безмежно малому впливу конвекції на перенос теплоти в середні краплі. Сказане дозволяє у першому наближенні знехтувати впливом конвекції. У загальному випадку термічний опір краплі, який визначається теплопровідністю, є верхньою границею процесу.

Під час руху ансамблю крапель спостерігається коагуляція окремих частинок. У дисперсних системах мають місце різні види коагуляції: броунівська (для всіх малих частинок), кінематична (обумовлена різницею швидкостей руху крапель), турбулентна (викликана взаємодією струменя краплин з суцільним середовищем, в який відбувається розпилення), електрична (при розпиленні дрібні частинки можуть бути зарядженими), акустична, гравітаційна (у зв'язку різної швидкості осадження різних крапель у зоні гальмування). При інтенсивному розпиленні найбільш суттєвими є кінематична і турбулентна коагуляції.

15.2. Статистичні характеристики

Диспергування струменю надає процесу чітко виражений статистичний характер, що дозволяє використовувати для його опису адекватні математичні методи. Основою побудови математичного опису процесу теплообміну служить рівняння

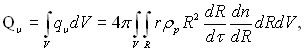(15.11)

в якому dR/dτ = w(R) – лінійна швидкість росту одиничної краплі, м/с;           φ(R) = dn/dR – диференціальна функція розподілу крапель за розмірами, м^–4;    dn – лічильна концентрація крапель даної фракції (R, R + dR); R – радіус краплі; q_υ  – об’ємна інтенсивність тепловиділень, Вт/м³.

Краплі вважаються сферичними. Рівняння (15.11) можна перетворити для випадку, коли краплі відхиляються від кулястої форми. Можна розглядати розподіл крапель по об’єму, масі та ін.

Рівняння (15.11) визначає тепловиділення по об’єму диспергованого струменя і аналогічно рівнянню (13.2), яке використовується для опису процесу крапельної конденсації.

Функція швидкості росту краплі w(R) і розподілу крапель за розміром φ(R) є тією основною інформацією, наявність якої принципово дозволяє отримати цифрові значення як локальних, так і інтегральних тепловиділень (чи середньомасових значень температури полідисперсної системи крапель). Вирази для w(R) і φ(R) залежать від умов постановки задачі.

Якщо швидкість росту краплі оцінювати інтенсивністю приросту її маси

то 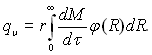(15.12)

Розглянемо найпростішу теорію теплообміну при конденсації пари на струмені диспергованої рідини, який рухається в парі у напрямку осі х. Для опису швидкості росту краплі використаємо рівняння (15.5)

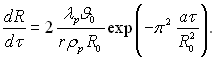
Функцію розподілу опишемо рівнянням:

З умови нормування визначаємо сталу величині, яка становить:

(15.13)

де середній арифметичний радіус; 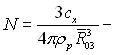локальне значення сумарної лічильної концентрації крапель усіх розмірів; с_х – локальна концентрація рідини у парі, кг/м³ ; R(₀₃ – середній об’ємний радіус системи крапель.

У відповідності з рівнянням (15.4) швидкість збільшення маси краплі буде

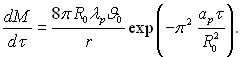(15.14)

Підставивши функції швидкості росту краплі (15.14)і розподілу за розмірами (15.13) в інтегральне рівняння (15.12), отримаємо:

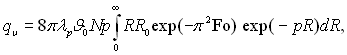(15.15)

де Fo = а_рτ/R₀². Покладемо R ≈ R₀ і введемо середній радіус R̃  системи крапель, який задовольняє співвідношення

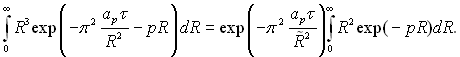
тобто 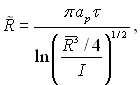де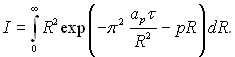

Тоді

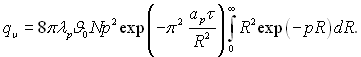(15.16)

Час перебування краплі в парі при її русі у напрямку осі х становить:

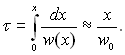
Ця рівність виконується тим точніше, чим менше відхилення швидкості w(x) від початкової.

Підставивши значення τ і виконавши інтегрування, з (15.16) отримаємо:

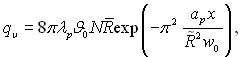
де 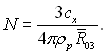В останньому рівнянні знаходяться три визначених різним способом радіуси краплі , і . Замінимо R| і R̃  середнім об’ємним радіусом R̃₀₃, враховуючи, що R|, R̃ і R̃₀₃  є величинами одного порядку. Внаслідок цього для локальної об’ємної густини тепловиділення отримаємо формулу:

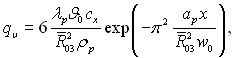(15.17)

чи у безрозмірній формі запису

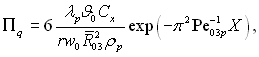(15.18)

де

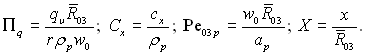
Інтегруючи це рівняння в межах від 0 до Х, отримаємо:

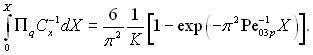(15.19)

Це рівняння визначає сумарне тепловиділення на ділянці 0...Х. Його безрозмірна величини становить при Х → ∞. При Х = 0 тепловиділення дорівнює нулю.

Формули (15.18) і (15.19) отримані при значних спрощеннях. Розглянемо більш повну постановку задачі.

Під час руху крапель функція розподілу останніх за розмірами може змінюватися. Ця зміна може відбуватися із-за змінної швидкості руху крапель різних розмірів, у зв'язку з розширенням струменя, із-за коагуляції і конденсаційного росту окремих крапель. Остання обставина не повинна відігравати значної ролі, тому що конденсація пари не приводить до значного збільшення одиничної краплі.

Розглянемо зміну функції розподілу крапель по масі φ(М) = (dn/dM), 1/(м²·кг), на ділянці конусоподібного струменя довжиною dx, якій відповідає збільшення перерізу струменя df і швидкість крапель даної фракції dw. Можна написати, що

(15.20)

чи з точністю до нескінченно малих першого порядку

(15.21)

Зміна, обумовлена коагуляцією, становить:

Розділимо рівняння (15.21) на φwf, отримаємо

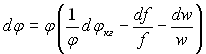
чи

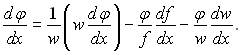(15.22)

Перший доданок правої частини цього рівняння враховує зміну функції розподілу за рахунок коагуляції. Другий доданок описує зменшення лічильної концентрації крапель у зв'язку з розширенням конусоподібного струменя. Третій – із-за зміни швидкості.

Вважаємо, що початкова функція розподілу φ₀ задана безперервною. Тоді на підставі зміни функції розподілу із-за коагуляції при урахуванні тільки парної взаємодії може описуватися рівнянням:

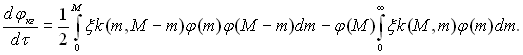(15.23)

Тут перший член правої частини враховує збільшення концентрації даної фракції із-за коагуляції більш дрібних крапель з фракції (m, m + dm), другий член – зменшення концентрації за рахунок коагуляції крапель даної фракції зі всіма іншими. У рівнянні (15.23) k – коефіцієнт коагуляції; ξ – коефіцієнт ефективності взаємодії крапель (0 ≤ ξ ≤ 1).

Для одномірного руху при урахуванні тільки кінематичної коагуляції коефіцієнт коагуляції становить:

(15.24)

де R, r – радіуси взаємодіючих крапель з масами відповідно М і т, які мають швидкості w(M) і w(m).

Коефіцієнт ефективності взаємодії крапель ξ ураховує ймовірність злиття крапель, що зіштовхуються. В основних розрахунках ξ вважається рівною одиниці, тобто всі зштовхування вважаються ефективними.

Зміну функції розподілу із-за розширення струменя визначимо у відповідності з умовою збереження маси рідини (без урахування конденсації)

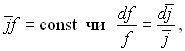(15.25)

де j( – середня в перерізі f густина потоку рідини. Густина потоку рідини залежить від параметрів розпилювання, властивостей рідини і координат. Вважаємо, що

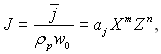(15.26)

де Х = х/R(₀₃; Z = z/R(₀₃ – безрозмірні координати (рис.15.3); a_j – аргумент, який залежить від параметрів розпилювання і властивостей рідини.

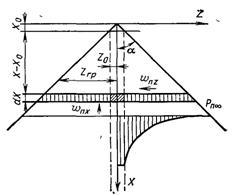
Рис.15.3. Схема конусного струменя крапель рідини

З (15.26) виходить, що

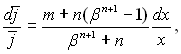(15.27)

де 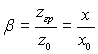(рис.15.3). Координати x₀, z₀ відповідають перерізу, в якому заданий початковий розподіл крапель.

У результаті цього другий доданок можна подати в наступному вигляді:

(15.28)

де

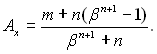(15.29)

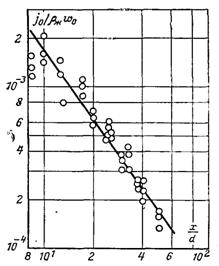
Рис.15.4. Зміна питомого потоку рідини по осі струменя: w₀ = 8,1…21 м/с; d = 4,01...6,02 мм; z₀/d = 1,58...2,38

Формулу (15.26) можна отримати дослідним шляхом. При опрацюванні дослідних даних вважалося, що j( на осі труби є кінцевою величиною. З дослідних даних (рис.15.4) виходить, що т = –1,44 на осі труби в області β  = 20...80, якщо а = π/4 (див. рис.15.3).

Підстановка виразів (15.23), (15.24) і (15.28) у рівняння (15.22) дає інтегрально-диференціальне рівняння лічильної концентрації крапель. Запишемо його з використанням безрозмірних змінних величин. Для функції φ(М) можна за масштаб взяти N₀/M(₀, де

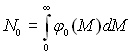
представляє собою сумарну кількість крапель усіх фракцій в одиниці об’єму в початковому перерізі (х = х₀), а M(₀ – масу краплі, яка відповідає середньому об’ємному радіусу системи крапель R(₀₃ у початковому перерізі. Масштабом швидкості призначимо величину w₀. Позначимо також

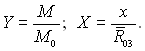
У прийнятих позначеннях рівняння лічильної концентрації крапель (рівняння лічильної рівноваги) можна записати в наступному виді:

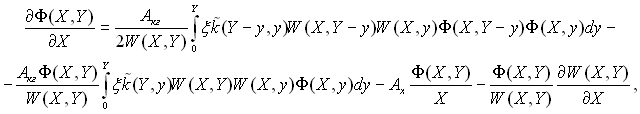
(15.30)

де Коефіцієнт А_кг можна подати в наступному виді:

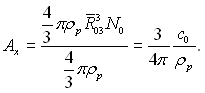(15.31)

Через с₀ позначається масова концентрація рідини у початковому перерізі х₀; Граничним випадком є с₀ = ρ_р, тоді А_кг = 3/(4π).

При коагуляції безперервний конденсаіцний ріст розглядуваної краплі супроводжується стрибковим збільшенням її маси і розміру за рахунок приєднувальної краплі. У подальшому вважаємо, злиття відбувається миттєво. Між злиттями швидкість конденсації визначається розміром і середньою температурою краплі. Приєднанні під час безперервного росту і коагуляції маси будемо відмічати індексами “кн” і “кг”. Разом з масами М_кн і М_кг передається ентальпія. Рівняння теплового балансу набуває наступного виду:

(15.32)

Якщо ввести безрозмірний прогрів краплі Θ = (Т – Т₀)/(Т_н – Т₀), то матимемо:

MdΘ + ΘdM = (K + 1)dM_кн.+ d(М_кгΘ_кг) (15.33)

чи

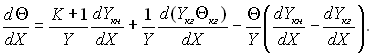(15.34)

де

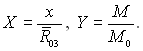
При К >> 1 (P ≈ 1, R ≈ R₀) рівняння безперервної швидкості росту краплі (15.9) можна подати у виді

(15.35)

де

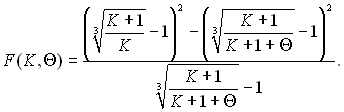(15.36)

У безрозмірній формі запису рівняння (15.35) можна представити так:

(15.37)

У формулах (15.35)...(15.37):

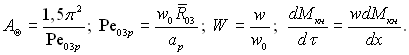
Швидкість росту контрольної краплі за рахунок приєднання більш дрібних з фракції (т, т + dm) дорівнює:

Сумарний ефект від взаємодії зі всіма фракціями m < M:

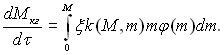(15.38)

Прирощення ентальпії при цьому складає:

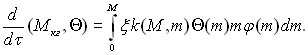(15.39)

Тут Θ(т) – безрозмірний прогрів крапель фракції (т, т + dm).

Рівняння (15.38) і (15.39) можна подати в безрозмірних змінних:

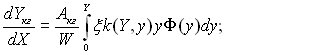(15.40)

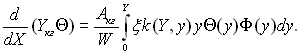(15.41)

Підставляючи значення функцій згідно (15.37), (15.40) і (15.41) у (15.34), отримаємо наступне рівняння швидкості прогріву краплі:

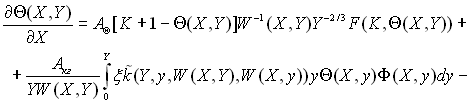(15.42)

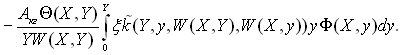
Швидкість краплі W(Y), яка входить в рівняння лічильної концентрації крапель і рівняння швидкості прогріву краплі, визначається рівнянням руху краплі:

(15.43)

Це рівняння, яке записане для центру маси краплі, відтворює рівновагу у кожну мить між силою інерції, з одного боку, і реактивною силою F_M аеродинамічного опору F_ψ і силою тяжіння F_g – з іншого боку.

Реактивна сила обумовлена як конденсацією пари на краплі, так і приєднанням інших крапель. показують, що при конденсації пари неметалевих рідин реактивна сила, обумовлена конденсаційним ростом краплі, зазвичай невелика у порівнянні з іншими силами. Реактивна сила за рахунок приєднання більш дрібних крапель за умови безперервності цього процесу і при одномірному русі може визначатися рівнянням:

(15.44)

де dM/dτ – швидкість зміни маси основної краплі;  и – швидкість її руху; υ  – швидкість приєднаних крапель.

Реактивна сила, як сума сил, обумовлених приєднанням окремих більш дрібних фракцій, становить

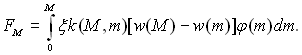(15.45)

Сила аеродинамічного опору описується рівнянням:

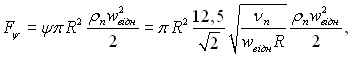(15.46)

де w_відн – швидкість краплі відносно пари; ν_п, ρ_п – коефіцієнт в’язкості і густина пари.

Підставляючи значення F_M, F_ψ  і F_g = Mg в (15.43), отримаємо рівняння руху краплі:

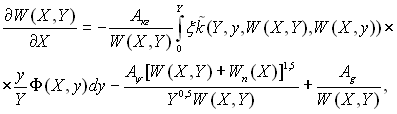(15.47)

де додатково використані наступні позначення:

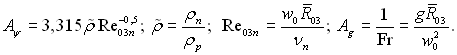
Рівняння швидкості росту краплі (15.42), лічильної концентрації (15.30) і руху краплі (15.47) дозволяють визначити температуру, концентрацію і швидкість крапель у поточному перерізі струменя. До системи рівнянь необхідно добавити умови однозначності:

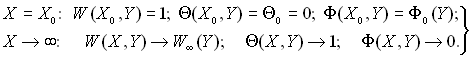(15.48)

Для визначення об’ємної густини тепловиділення необхідно використати рівняння (15.12), яке можна записати у безрозмірному виді

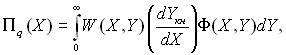(15.49)

де

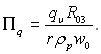
При цьому використана умова тому що в початковому перерізі концентрація рідини прямує до її густини. Значення похідної dY_кн/dX визначається рівнянням (15.37).

15.3. Теплообмін при конденсації на диспергованій рідині

Внаслідок процесу конденсації може виникнути рух пари в початковій області струменя. Вектор швидкості пари має по крайній мірі дві складові: повздовжню w_x і радіальну w_z. Швидкість пари залежить від умов його подачі в робочий простір конденсатора.

Нехай пара надходить назустріч струменю. На віддалі від сопла пара буде рухатися переважно в напрямку протилежному напрямку течії струменя. Поблизу від сопла пара має помітну радіальну складову швидкості. Співвідношення величин w_x і w_z може визначатися енергетичними затратами на переміщення пари в системі крапель. У першому наближенні втрати тиску рухомої пари можна вважати рівними сумі аеродинамічних втрат, обумовлених обтіканням окремих крапель.

Виходячи із співвідношення величин w_x і w_z, можна виділити переріз з координатою Х_кр. При Х > Х_кр переважає осьовий рух пари; при Х < Х_кр радіальна складова швидкості пари має помітну величину. Оцінку критичного перерізу Х_кр можна зробити для конкретних умов процесу.

Стосовно з експериментами, які розглянемо нижче, отримано, що критичний переріз наближено відповідає значенню

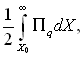
де П_q визначається з рівняння (15.49).

У розрахунках осьова швидкість пари оцінювалася рівняннями:

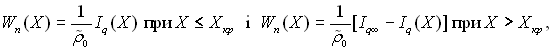
де

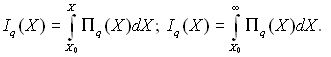
При достатньо великій відносній швидкості руху можливий розпад краплі. Роздвоєння краплі настає, коли

чи у безрозмірній формі запису

де

Співвідношення для швидкості пари і розпаду крапель використовувалися при числових розрахунках. У розрахунках задавалися значення Y_i, які входять у рівняння (15.30), (15.42) і (15.47), а також початкові значення функцій W_i(X), Ф_і(Х), Θ_і(Х) для кожної фракції. Змінними, які визначали варіант розрахунку, були швидкість рідини w₀, середній об’ємний радіус крапель у початковому перерізі R(₀₃, число фазового переходу К і функція розподілу в початковому перерізі.

Виконано десять варіантів розрахунків без урахування коагуляції. В перших чотирьох варіантах w₀ = 10; 15; 20; 25 м/с; R(₀₃ = 126,1 мкм; К = 7,62. Початкова функція розподілу приймалась згідно вимірювань В.І.Кушнарева. Чотири наступних варіанта відрізнялися тільки початковою функцією розподілу, яка відповідала більш тонкому подрібненню. Середній об’ємний радіус для цієї функції дорівнював 43,6 мкм. У двох останніх варіантах w₀ = 15 м/с; К = 10,67. Функція розподілу Ф₀ приймалася такою ж, як і в перших чотирьох варіантах.

Додатково виконані розрахунки з урахуванням коагуляції при w₀ = 15 м/с, R(₀₃ = 126, 1 мкм, К = 7,62. Функція розподілу аналогічна першим варіантам розрахунків, але інтервали зміни безрозмірної маси прийняті рівними 0,2. При цьому діапазон зміни радіуса крапель Ф₀ звужується і стає рівним 70...200 мкм замість 12,5...1000 мкм у варіантах без урахування коагуляції.

Розрахунки з урахуванням коагуляції показали, що при різних значеннях коефіцієнта ефективності зштовхувань загальна величина теплового потоку змінюється слабко. При зміні ξ від 0 до 1 величина І_q0 змінюється приблизно від 0,0179 до 0,0169.

Дані розрахунків використані для уточнення формули (15.19), отриманої з використанням елементарної теорії. Для

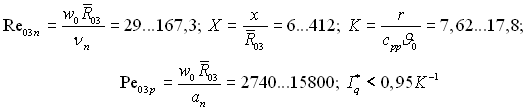
запропонована розрахункова формула:

(15.50)

де Q_υ(X) – тепловиділення на ділянці струменя від Х = Х₀ до Х, Вт; G – масовий потік рідкої фази, кг/с.

Середнє квадратичне відхилення розрахункових точок від залежності (15.50) складає 12%, дисперсія кривої (коридор помилок) не перевищує 1%.

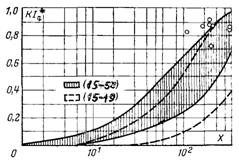
Рис.15.5. Залежність безрозмірного теплового потоку від повздовжньої координати:  – дослідні точки

На рис.15.5 наведено порівняння величин безрозмірного теплового потоку , які визначені за рівняннями (15.19) і (15.50). Точки на графіку відповідають результатам експериментальних досліджень конденсації пари на струмені диспергованої води.

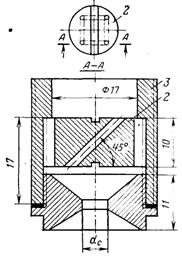
Рис.15.6. Відцентрова форсунка: 1 – сопло; 2 – завихрювач; 3 – корпус

Досліди виконувалися при витіканні води через відцентрову форсунку в водяну пару. Форсунка знаходилася у верхній кришці баку діаметром 516 мм і висотою 1800 мм. Використовувалися спеціально виготовлені форсунки (рис.15.6) з діаметром сопла 4,01; 4,98; 6,02 мм. До конденсатору надходила як чиста насичена пара приблизно атмосферного тиску (перегрів не перевищував 1 К), так і пара з добавкою азоту. Струмінь розпадався на ансамбль крапель безпосередньо при виході з сопла; суцільна ділянка струменя не спостерігалася.

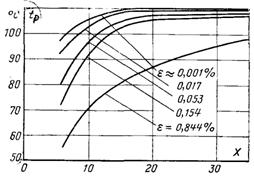
Рис.15.7. Вплив вмісту азоту у водяній парі на прогрів води

Досліди з паро-газовою сумішшю показали суттєву залежність швидкості прогріву води від вмісту азоту в парі (рис.15.7). Безрозмірну середню температуру струменя диспергованої води Θ = (Т – Т₀)/(Т_н – –Т₀), де Т₀ – температура води на вході в конденсатор, можна визначити з рівняння:

(15.51)

де Lp = ρ_pσd_c/μ_p² – число Лапласа; К = r/c_pp(Т_н – Т₀) – число фазового переходу;  А = R_зr₀/nr_вх² – безрозмірна геометрична характеристика форсунки; R_з – радіус закручування рідини у камері форсунки; r₀ – радіус сопла; п, r_вх – кількість тангенціальних вхідних каналів і їх радіус; ε = т_г/т_п – масовий вміст газу на вході суміші у конденсатор; Z = z/2r₀, X = x/2r₀ – координати. Швидкість w₀ розраховувалася за витратами води через форсунку за діаметром сопла d_c = 2r₀.

Фізичні параметри води ρ_р, μ_р, с_рр вибираються по температурі Т₀, а σ, r,   ρ_п – за Т_н. Рівняння (15.51) отримано для наступного діапазону величин:

Lp = (6,56...29,3)10⁵; К = 7,60...18,7; А = 1,13...1,70; ε  = (0,001...0,84)10^–2;

Z = 0,42…9,37; X = 4,65...47,4.

При цьому Θ  = 0,20...0,98. Середнє квадратичне відхилення дослідних даних від апроксимаційної кривої не перевищує 10%, дисперсія апроксимаційної функції (коридор похибок) не більше 1,5%.

При дослідженні параметри розпилювання визначалися при ізотермічному витіканні води в повітря. У цьому випадку середньо об’ємний радіус можна описати наступною залежністю:

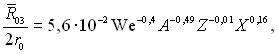(15.52)

яка справедлива при We = 5,67...28; А = 1,13...1,70; Z = 2,0…33,5; X = 14,4…246.

Безрозмірний питомий потік рідини:

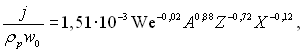(15.53)

при цьому We = 6,5...29,2; А = 1,13...1,70; Z = 1,58…41,8; X = 8,31…49,9.