Частина четверта. ТЕПЛООБМІН ПРИ ЗМІНІ АГРЕГАТНОГО СТАНУ. КИПІННЯ

     Розділ 17. РІВНОВАГА СИСТЕМИ РІДИНА – ПАРА І ВИНИКНЕННЯ В НІЙ ПАРОВОЇ ФАЗИ

17.1. Умови рівноваги

Найбільш простими і очевидними є умови термодинамічної рівноваги однорідної системи. Вони криються в тому, що в стані рівноваги у всіх частинах системи тиск і температура залишаються однаковими. Тоді при постійних зовнішніх умовах стан системи не буде змінюватися в часі. Це виходить з другого початку термодинаміки і поняття ентропії і може бути отриманим з умови dS = 0, яка відповідає максимуму ентропії ізольованої системи.

Для можливості стійкої рівноваги однорідної системи, повинні виконуватися теж очевидні умови: а) теплоємність системи повинна бути додатною величиною; б) із збільшенням її об’єму повинен зменшуватися тиск, тобто похідна за об’ємом при сталій температурі повинна бути від’ємною величиною

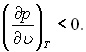(17.1)

Система рідина – пара є гетерогенною двофазною системою, а кожна із складових її фаз представляє собою однорідну систему. Поняття фази включає не тільки визначення її як агрегатного стану, чи алотропічної різновидності речовини, але і уяву про існування поверхні розділу, яка відокремлює цю фазу від інших фаз, що складають систему. Перехід речовини з одної фази до іншої називається фазовим переходом чи фазовим перетворенням. У системі рідина – пара ці переходи відбуваються у вигляді випарювання і конденсації.

Умови рівноваги гетерогенних систем і стійкості фаз установлені Гіббсом. Ним виконаний аналіз і розв’язок цієї складної проблеми у її різних аспектах на основі введення поняття хімічного потенціалу. До багато чисельних результатів, отриманих Гіббсом, відноситься створення основ теорії кипіння.

Питання про рівновагу системи рідина – пара розглядується з допущенням, що система не підлягає дії сил немеханічного походження (електричні, магнітні), і виходячи з цього, приймаються до уваги тільки сили обумовлені тиском.

Умова найбільш простої задачі про рівновагу зводиться до того, що протяжність фаз і їх поверхонь розділу достатньо великі. Виходячи з цього, поверхневою енергією системи можна знехтувати у порівнянні з її об’ємною енергією. У цьому випадку умовою рівноваги замкненої системи рідина – пара є рівність температур, тисків і хімічних потенціалів рідини і пари:

(17.2)

Тут хімічний потенціал μ – це термодинамічний потенціал Гіббса

Ф = U – NS + pV,

який віднесений до одиниці маси чи одиничної частинки.

Рівність температур і хімічних потенціалів випливає з незмінності розподілу ймовірності стану в даній системі. Якщо система знаходиться у рівновазі, то взаємодія між фазами не повинна впливати на зміну фаз у системі в цілому. Виконання умов механічної рівноваги вимагає того, що при невиконанні цих умов має місце переміщення границі розділу фаз і, таким чином, порушення рівноваги в системі.

Рівність температурних і хімічних потенціалів випливає з необхідності незмінного розподілу ймовірності стану в даній системі. Якщо система знаходиться в рівновазі, то взаємодія між фазами не повинна призводити до зміни стану фаз у системі у цілому. Виконання умови механічної рівноваги необхідно тому, що при незбереженні її мало б місце зміщення границі розділу фаз і, таким чином, порушення рівноваги в системі.

З рівності μ(р, Т) = μ_п(р, Т) можна отримати рівноважний тиск у залежності від рівноважної температури р = р_н(Т). У координатах (р, Т) ця залежність представляє собою криву фазової рівноваги однокомпонентної системи. Для багатокомпонентних систем залежність між р і Т не має місця. Рівноважність фаз рідина – пара у таких системах можлива при різних значеннях р і Т і при відповідній зміні складу фаз. У подальшому розглядатимемо однокомпонентні системи.

У просторі μ, р, Т рідина і пара характеризуються відповідними поверхнями хімічного потенціалу μ(р, Т) і μ_п(р, Т). Крива фазової рівноваги р = р_н(Т) утворюється перетином цих поверхонь. Точки на цій кривій належать обом поверхням, що визначає рівність хімічних потенціалів обох фаз. На рис.17.1 наводяться сліди цих поверхонь у площинах p = const і T = const.

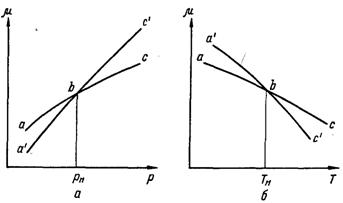
Рис.17.1. Сліди поверхонь хімічного потенціалу рідини і пари на площинах T = const (а) і p = const (б)

Вигляд кривих

μ = μ(р) і          μ = μ(Т) можна вияснити з основних

.

17.2. Стійкість фаз

Стійкою є фаза, яка має при даних р і Т більш низькі значення хімічного потенціалу. Це слідує з того, що під час переходу системи до рівноважного стану при сталих р і Т її хімічний потенціал Ф зменшується. Таким чином, ділянка ab на рис.1,б відповідає стійкому стану рідини, а ділянка bc – метастабільній перегрітій рідині. Метастабільним станом рідини називають не повністю стійкий її стан (відносно стійкий стан), який має місце при перегріві рідини до температури, що перевищує температуру насичення, яка відповідає даному тиску. При цьому відбувається перехід через криву рівноваги без фазового перетворення. Бінодаль (крива фазової рівноваги) у просторі μ, р, Т є границею абсолютно стійких станів рідини і пари.

Нагріваючи чисту рідину, яка не містить ні твердих частинок, ні газових бульбашок, можна досягнути значного її перегріву. Але у такому метастабільному стані речовина не може знаходитися довгий час. Після певного проміжку часу вона перейде до стійкого стану. У цьому випадку фазовий перехід відбувається при температурах значно вищих рівноважних температур, які перевищують рівноважну температуру кипіння при даному тиску.

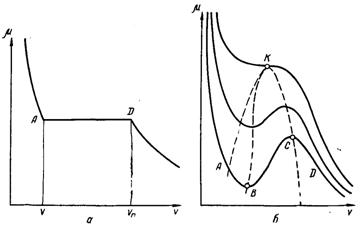
Рис.17.2. Хід ізотерм μ(υ)  для рівноважного фазового переходу (а) і при утворенні метастабільного стану (б) (А – рідина, D – пара)

Границі метастабільного стану рідини пояснюються з розгляду ізотерми хімічного потенціалу, який відображає залежність μ = μ(υ) для рівноважного фазового переходу, коли метастабільний стан рідини не утворюється, наведений на рис.17.2,а. При утворенні метастабільного стану ізотерма μ = μ(υ) набуває вигляду, показаного на рис.17.2,б. У цьому випадку після того, як питомий об’єм рідини досягає значення υ, що відповідає Т_н, розшарування речовини на рідку і парову фази не спостерігається, а відбувається вторгнення вихідної (рідкої) фази в чужу область. Це відповідає плавному переходу від точки b вправо по лінії ас (див. рис.17.1) і знаходить своє відображення в ході ізотерми хімічного потенціалу рідкої фази. Починаючи з точки А (рис.17.2,б) крива μ = μ(υ) рідкої фази має продовження на ділянці АВ, яка відповідає метастабільному стану перегрітої рідини. Аналогічно ділянка DC відповідає метастабільному стану парової фази.

Справа від точки В лінія ВС проходить так, що на цій ділянці (дμ/дυ)_Т  > 0, а тому що (дμ/др)_Т  = υ(др./дυ), то (др/дυ)_Т  > 0, тобто не виконується умова стійкості однорідної системи. Отже, у цій області значень υ можливе існування тільки двофазної системи. Тому після того як питомий об’єм рідини досягає значення, що відповідає точці В, її існування як однофазної системи неможливе. Цим визначається теоретична (термодинамічна) границя метастабільного стану рідини.

Якщо побудувати ряд ізотерм μ = μ(υ) аж до критичного значення температури Т_кр і провести лінію, яка проходить через точки на ізотермах, аналогічним точці В, в яких (дμ/дТ) = 0, то ця лінія буде представляти собою граничну лінію для граничного перегріву рідини (спінодаль). На рис.17.2,б ліворуч від спінодалі показана бінодаль. Область метастабільного стану рідини знаходиться між бінодаллю і спінодаллю.

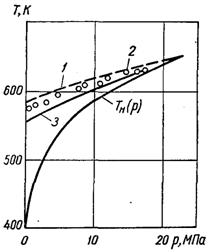
Рис.17.3. Порівняння дослідних даних про граничний перегрів води з розрахунком: 1 – за теорією гомогенної нуклеації; 2 і 3 – за рівняннями Гімпана і Вукаловича-Новікова

На рис.17.3 наводиться співставлення розрахункових і дослідних даних про граничний перегрів води, яке свідчить про погодженість теорії і досліду.

Питання про стійкість метастабільного стану рідини можна розглядати в різних аспектах. Якщо існують причини, які сприяють утворенню в перегрітій рідині великих парових утворень, то у цьому випадку метастабільний стан нестійкий. Якщо реальні умови такі, що ймовірність спонтанного утворення великої маси парової фази дуже мала, тому що дуже малі подразнення, які викликають флуктуації, то рідина може існувати тривалий час у метастабільному стані. На кінець, можливий також метастабільний стан рідини, який визначається спінодаллю, при цьому рідка фаза нестійка до відносно малих змін її параметрів. За цієї умови тривале існування рідини у метастабільному стані неможливе.

17.3. Утворення парової фази в об’ємі рідини

В однорідній системі внаслідок теплового руху з характерною йому невпорядкованістю виникають флуктуації густини. Якщо рідина недогріта до температури насичення при даному тиску, то рідка фаза абсолютно стійка і локальні флуктуації густини не отримують в ній розвитку: вони зникають і стан системи не змінюється. У цьому випадку рідка фаза стійка до відносно великих подразнень. Навіть внесення до неї затравок, які у перегрітій рідині сприяють появі великих парових утворень, не може привести до виникнення парової фази.

Перегріта (метастабільна) рідина знаходиться у відносно стійкому стані. У ній внаслідок виникнення флуктуацій можливе утворення парової фази, але для цього потрібно подолати певний бар’єр, обумовлений дією поверхневих сил.

Механізм утворення парової фази у перегрітій рідині можна представити у загальних рисах наступним чином. У невеликому об’ємі вихідної однорідної рідини внаслідок флуктуацій густини утворюються дрібні включення парової фази у вигляді мікроскопічних парових бульбашок. Бульбашки дуже малих розмірів нестійкі (нежиттєздатні). Із збільшенням перегріву рідини, з одного боку, збільшується ймовірність виникнення флуктуацій відносно великого масштабу (ймовірність виникнення відносно великих включень парової фази), з іншого – зменшується розмір життєздатних бульбашок. При достатніх розмірах парових утворень вони стають стійкими і служать центрами пароутворення, які продовжують рости.

Нестійкість дрібних бульбашок пояснюється тим, що при недостатніх розмірах включень парової фази робота зміни об’єму не може компенсувати енергетично невигідний ефект з’явлення поверхні розділу між рідиною і парою (чим менша бульбашка, тим більше відношення її поверхні до об’єму). Тому для рідини у метастабільному стані існують певні мінімальні розміри, які повинні мати парові утворення для того, щоб парова фаза була стійкою. При малих розмірах парових утворень рідка фаза стійка відносно таких флуктуацій і виниклі бульбашки не розвиваються, а зникають.

Життєздатні бульбашки, які досягли необхідного мінімального розміру, називаються зароками парової фази. Зародки знаходяться в нестійкій рівновазі з рідкою фазою. Відносно менших бульбашок рідина стійка, а відносно крупних – парова.

Для кожного метастабільного стану рідини існує певне мінімальне значення масштабу флуктуації, яке приводить до початкової стадії фазового переходу – утворенню і початковому росту парової фази. При виникненні гетерофазних флуктуацій такого і більшого масштабу забезпечується спонтанне зародкоутворення у метастабільній фазі. Цей процес передує розвитку процесу кипіння у макроскопічних масштабах з утворенням великої кількості парової фази.

У загальному випадку в умовах рівноважного стану фаз дотримується рівність їх температур Т = Т_п і хімічних потенціалів μ = μ_п і має місце механічна рівновага. Для того щоб виниклі бульбашки були життєздатними, а не зникли миттєво, і могли існувати певний час, необхідно дотримуватися умов рівноваги фаз.

Зміна розмірів поверхні розділу фаз супроводжується здійсненням роботи. Якщо ця зміна відбувається при постійній температурі, то робота зміни поверхні дорівнює зміні вільної енергії. Вільна енергія одиниці поверхні σ (чи сила, яка діє на одиницю довжини на поверхні розділу фаз) називається коефіцієнтом поверхневого натягу. Поверхневий натяг змінює умову механічної рівноваги фаз. Сила, викликана поверхневим натягом, становить:

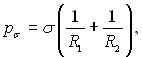(17.3)

де R₁ і R₂ – головні радіуси кривизни поверхні у даній точці.

Ця сила діє перпендикулярно до поверхні розділу фаз і спрямована всередину парової фази. Формула (17.3) називається формулою Лапласа, а р_σ  – капілярним тиском (тиском Лапласа). Для плоскої поверхні розділу (R₁ = R₂= ∞) капілярний тиск перетворюється в нуль і тиск в обох фазах стає рівним (р_п = р).

Тому що розміри парових зародків дуже малі, можна знехтувати впливом на їх форму сили тяжіння і прийняти, що вони мають сферичну форму (головні радіуси кривизни поверхні розділу фаз мають у усіх точках значення, рівне радіусу кулі R), за якої для даного об’єму поверхня розділу має мінімальну величину. Тоді формула (17.3) набуває виду:

(17.4)

Для механічної рівноваги необхідно, щоб сума всіх сил, діючих на поверхню розділу фаз, дорівнювала нулю. Звідси слідує:

(17.5)

тобто тиск у паровій фазі більший за тиск у рідині і врівноважується сумою тисків у рідкій фазі і капілярним тиском.

Наявність викривленої поверхні розділу фаз змінює умови не тільки механічної рівноваги. Необхідно враховувати і інший ефект, який пов’язаний з кривизною поверхні розділу. Він криється в тому, що тиск насиченої пари над викривленою поверхнею не дорівнює тиску насиченої пари над плоскою поверхнею.

У випадку плоскої поверхні розділу фаз даній температурі насиченої пари Т_н відповідає деяке загальне значення рівноважного тиску парової і рідкої фаз р_н. При викривленій поверхні розділу тиск пари р_п, який відповідає температурі насиченої пари Т_н, за умови рівно важності фаз, не дорівнює р_н. Він залежить від кривизни поверхні розділу і становить:

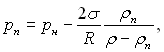(17.6)

а для рідини тиск буде

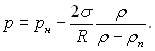(17.7)

Цей результат можна отримати різними шляхами: з умови рівноваги хімічних потенціалів μ_п(р_п, Т_н)  = μ(р, Т_н) з урахуванням ізотермічної зміни хімічного потенціалу dμ = υdp, і з розгляду умов механічної рівноваги у капілярній трубці радіусом R.

Тому що для ввігнутої поверхні радіус кривизни додатний, то тиск пари в паровій бульбашці сферичної форми над ввігнутою поверхнею розділу менший тиску пари над плоскою поверхнею при тій же температурі на величину

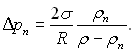
Аналогічно можна отримати значення Δр_п над випуклою поверхнею розділу – над сферичною краплею рідини, яка оточується парою. У цьому випадку тиск пари більший за тиск над плоскою поверхнею, що було вперше показано Томпсоном (лордом Кельвіном).

Тиск рідини при ввігнутій поверхні розділу і температурі пари Т_н менший його тиску при плоскій поверхні розділу на величину 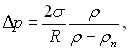яка представляє собою суму 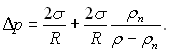Перший доданок цієї суми обумовлює поверхневий натяг, другий – кривизна поверхні розділу.

При розгляді задачі про рівноважний паровий зародок тик рідини задається і виникає обернена задача – знаходження температури насиченої пари у сферичному паровому зародку і необхідного перегріву рідини ΔТ=Т_н(р_п)–Т_н(р) Оскільки заданій температурі насичення відповідає менший тиск рідини, ніж р_н для плоскої поверхні, то заданому тиску рідини відповідає більш висока температура насиченої пари у зародку. Це збільшення температури насичення ΔТ у порівнянні з Т_н для плоскої поверхні розділу відповідає величині Δр. Його можна знайти наближено, але з достатньою точністю, враховуючи, що Δр  мале у порівнянні з абсолютним тиском рідини, і використавши рівняння Клапейрона – Клаузіуса. Воно виражає залежність рівноважного тиску фаз від температури, містить у правій частині величини, які легко можна виміряти, і яке можна застосувати для плоскої поверхні і для сфери:

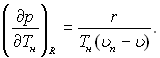(17.8)

Тоді (при невеликих значеннях ΔТ)

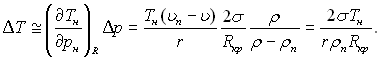(17.9)

Якщо ΔТ задана, то з (17.9) можна визначити радіус рівноважного парового зародка, який відповідає заданому перегріву рідини. Це критичний радіус зародка при заданому ΔТ :

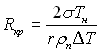(17.10)

чи мінімальний радіус життєздатних парових зародків.

Формулу для мінімальної роботи L, необхідної для утворення зародка і рівній різниці термодинамічного потенціалу системи після і до утворення зародка (тобто для роботи оборотного утворення парової фази в об’ємі рідини з урахуванням поверхневої частини вільної енергії), можна отримати, якщо виразити потенціал системи після і до утворення парової фази через хімічний потенціал рідкої і парової фаз.

Якщо число частинок в рідкій фазі позначити через N, а в паровій через N_n, то очевидно, потенціал системи до утворення парової фази буде:

(17.11)

Після утворення парової фази повний термодинамічний потенціал системи:

(17.12)

де μ(р, Т) і μ_п(р, Т) – хімічні потенціали фаз, віднесені до початкових умов, тобто без урахування ефекту утворення поверхні розділу фаз і пов’язаного з ним підвищенням тиску в зародку.

Різниця потенціалів дорівнює роботі оборотного утворення парової фази і становить:

(17.13)

Об’єм скупчення υ_п = υ₀N_n, де υ₀  – об’єм, який приходиться на одну частинку в паровій фазі. Якщо R – радіус скупчення, то 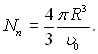Тоді

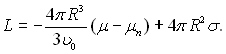(17.14)

У випадку утворення зародка – скупчення, яке має радіус R_кр, то система знаходиться у стані нестійкої рівноваги. Нестійкість рівноваги між перегрітою рідиною і зародком (бульбашкою пари радіусом R_кр) обумовлена тим, що потенціал утвореної ними системи має при R = R_кр не мінімальне значення, як при стійкій термодинамічній рівновазі, а максимальне. Радіус зародка R_кр визначається умовою нестійкої рівноваги дL/дR = 0. При цьому з рівняння (17.14) виходить, що

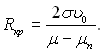(17.15)

У той же час при рівності 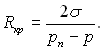Прирівнюючи ці вирази, отримаємо , і вираз для L приводиться до виду:

(17.16)

З (17.15) виходить, що

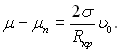(17.17)

Рівняння (17.17) виконується при тиску р_п, який відрізняється від р і залежному від радіусу зародка R_кр. У граничному випадку при R = ∞ це рівняння зводиться до звичайної умови рівноваги для плоскої поверхні розділу фаз μ = μ_п при рівноважних температурі і тиску.

В умовах рівноваги системи рідина – парова бульбашка безумовно виконується рівність хімічних потенціалів фаз, віднесених до загальної рівноважної температури, але відповідно до різних тисків фаз. Дійсно, якщо р_п – р невелика у порівнянні з р, то замість очевидної рівності μ_п(р_п)=μ_п[р+(р_п– –р)] можна наближено написати 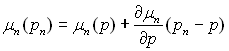чи, тому щ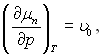о то З (17.17) виходить, що 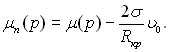Тоді

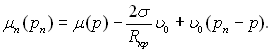(17.18)

Тому що 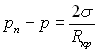, то при рівноважному стані системи парова бульбашка – рідина

(17.19)

Підставляючи у формулу (17.14) замість 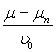з (17.17) можна виразити L такою залежністю:

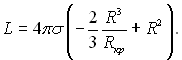(17.20)

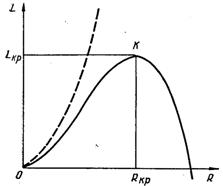
Рис.17.4. Характер залежності роботи утворення зародка від його радіуса

Зі збільшенням R від нульового значення L спочатку збільшується, досягаючи при R = R_кр максимального значення

(17.21) а далі знову зменшується. Хід кривої L у залежності від R у випадку метастабільного стану перегрітої рідини, коли μ > μ_n, наведений на рис.17.4. У точці К робота утворення поверхні найбільше перевищує роботу зміни об’єму, потенціал системи досягає максимуму, і система знаходиться у стані нестійкої рівноваги.

Починаючи з критичного розміру R_кр парові зародки можуть рости, тому що ріст супроводжується зменшенням термодинамічного потенціалу системи і переходом її у стан більшої ймовірності. Скупчення парової фази з розмірами меншими R_кр небажані, і такі флуктуації зникають. Отже, якщо μ > μ_n, то повинно розпочинатися перетворення рідкої фази у пару, тому що у цьому випадку стійкою є парова фаза, яка має менший хімічний потенціал. Проходження процесу обумовлене необхідністю подолання певного потенціального бар’єру L_кр.

Оскільки виникнення гетерогенної флуктуації, яка приводить до утворення парового скупчення, більш ймовірне для малої кількості частинок метастабільної рідини, ніж для великої їх кількості, то кількість парових скупчень безперервно зменшується зі збільшенням їх радіуса. З кривої зміни L(R) можна зробити висновок про характер розподілу кількості скоплінь пари у залежності від їх розмірів тільки в області значень R ≤ R_кр, де більшим розмірам R відповідає більший приріст термодинамічного потенціалу системи. Екстраполяція цього висновку на область значень R > R_кр незакономірна. Вона призводить до невідповідного дійсності наслідку. Це пояснюється тим, що закон розподілу парових скоплінь різного розміру, який випливає з чисто термодинамічних міркувань, не враховує усіх сторін реальної фізичної моделі процесу, такого як взаємодії між скопліннями утвореної парової фази, і тому для вирішення цієї задачі не може застосовуватися.

Якщо μ < μ_n, то при довільних значеннях радіуса скупчення приріст термодинамічного потенціалу додатний L > 0 і при збільшенні R термодинамічний потенціал системи безперервно і швидко збільшується, як це показано пунктиром на рис.17.4. Парова фаза термодинамічно нестійка, і виниклі в рідкій фазі флуктуації зникають, не отримавши свого розвитку.

Отриману раніше наближену формулу (17.10) для визначення критичного радіуса зародка R_кр при відомому перегріві рідини ∆Т можна отримати з (17.15). Для цього необхідно відшукати різницю віднесених до одиниці маси хімічних потенціалів рідини  μ і пари μ_n при Т = Т_н+ ∆Т. Для відносно невеликих перегрівів така різниця буде наближено рівна r∆Т /T_н. Після підстановки цієї величини у формулу (17.15) і заміни υ₀  на питомий об’єм пари отримаємо формулу (17.10).

Підставляючи в (17.21) замістьR_кр його значення з умови механічної рівноваги фаз, отримаємо наступний вираз:

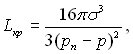(17.22)

в який не входить у явному виді радіус критичного зародка.

Якщо прийняти ряд спрощень, які допустимі для помірних тисків і перегрівів, і виключити з формули (р_п – р) і, використовуючи рівняння Клапейрона – Клазіуса, ввести замість різниці тисків перегріву рідини, можна отримати наближене співвідношення, з якого слідує, що L_кр обернено пропорціональна ∆Т ². Отже, робота утворення зародка різко зменшується, а ймовірність його утворення відповідно різко зростає зі збільшенням перегріву рідини ∆Т .

Робота утворення зародка є основним параметром, який визначає мікрокінетику фазових перетворень. В основі уявлень про кінетику зародкоутврення взагалі і кінетику процесу кипіння на початковій стадії в окремому випадку лежить ідея Гіббса, який запропонував вважати мірою стійкості метастабільної фази роботу утворення критичного зародку L_кр.

Ймовірність утворення парового зародку – це ймовірність флуктуації, за якої у метастабільній рідині утворюється скупчення пари з радіусом R_кр. Ймовірність такої флуктуації пропорційна 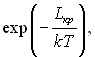де k – стала Больцмана. Кінетична теорія гомогенного зародкоутворення є наслідком роботи багатьох дослідників і зокрема В.П.Скрипова.

Ґрунтуючись на ідеї Гіббса і термодинамічних міркуваннях отримано наближений вираз для кількості зародків J, які виникають в одиниці об’єму метастабільної фази в секунду, який в скороченій формі запису має вид:

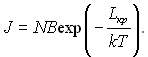(17.23)

Величина J представляє собою частоту спонтанного зародкоутворення; N – кількість молекул в одиниці об’єму; В – стала величина, яка є функцією стану системи (відносно слабка функція). Головним чинником, який визначає величину J, є експоненціальний множник.

У подальшому розвиток теорії зводиться до детального розгляду елементарних актів випаровування і конденсації з більш поглибленим використанням кінетичних уявлень. При цьому вважається, що швидкість росту парових скупчень визначається швидкістю процесу випаровування і конденсації, а вплив в’язких і інерційних сил дуже малий. При цьому формула для частоти зародкоутворення набуває вид:

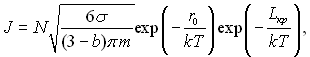(17.24)

де b = p/p_n при b < 3; т – маса молекули; r₀ – теплота випаровування, віднесена до однієї молекули (енергія активації процесу дифузії молекул).

Можливості наближеної теорії обмежені областю додатних і невеликих від’ємних тисків, що відповідає значенню b < 3. При великих розрідженнях висновки цієї теорії суперечать термодинамічним уявленням, які покладені в основу.

Головний результат теорії зародкоутворення криється у завбаченні можливості високих перегрівів чистих рідин, хоч в оцінці J, що відповідає граничному перегріву, криється певна невизначеність. Але це практично не впливає на точність визначення граничних температур рідини, тому що зміні J у формулі (17.24) на десять і більше порядків веде до зміни температури тільки на 2...4°С. Виходячи з цього, значення передбачені теорією граничних перегрівів в широкому діапазоні значень J задовільно погоджується з дослідними даними для води і органічних рідин і з розрахунковими рівняннями, отриманими за рівняннями стану речовини.

Можливості практичного використання теорії зародкоутворення в інших аспектах обмежені. Це пояснюється наближеним характером теорії – використанням для розв’язку задачі мікрокінетики мікроскопічних величин (σ  і р_п), використанням властивостей пари в зародках як ідеального газу і ряду інших не повністю обґрунтованих уявлень. Але найбільш суттєвим є те, що в реальних умовах (не тільки в технічних пристроях, але і в дослідній практиці) у рідинах завжди знаходяться тверді, колоїдні чи газові включення і інші слабкі місця, які значно полегшують закипання. Тому для кипіння рідин практично достатньо значно нижчих перегрівів, ніж передбачені теорією для чистих рідин.