17.4. Виникнення зародків на твердій поверхні

Якщо рідина знаходиться у контакті з твердою поверхнею, до якої підводиться теплота зі зростаючим тепловим потоком і відповідно зі зростаючою температурою поверхні нагріву, то при досягненні певного (достатнього) перевищення температури поверхні над температурою насичення рідини на поверхні нагріву починається процес кипіння. На ній виникають парові зародки, тому що рідина найбільш перегріта у тонкому пристінному шарі, який дотикається до твердої поверхні. При цьому фазовий перехід відбувається на шорстких поверхнях при перегрівах рідини значно менших, ніж у випадку кипіння чистої рідини в об’ємі.

Процес кипіння на твердій поверхні відбувається у більш складних умовах, ніж об’ємне кипіння. Його складність і закономірності визначаються сумісним впливом ряду додаткових, у порівнянні з кипінням в об’ємі рідини, факторів – геометричних характеристик і теплофізичних властивостей поверхні нагріву, фізико-хімічної взаємодії фаз, суттєвою температурною нерівномірністю. Аналітичний опис такого процесу і отримання теоретичних рішень у цьому випадку ускладнюється. Для наближеного аналізу питання виникнення кипіння на твердій поверхні зазвичай користуються основними положеннями теорії зародкоутворення, розглянуті при кипінні в об’ємі чистої рідини.

Розгляд особливостей процесу кипіння на твердій поверхні необхідно розпочинати із задачі про зародкоутворення на гладкій горизонтальній поверхні. Для виявлення ролі твердої поверхні необхідно визначити роботу утворення парового скупчення, яка є мірою ймовірності виникнення парової фази. Для малих парових скупчень нехтують впливом сили тяжіння і вважають, що зародки мають форму кульового сегменту (рис.17.5).

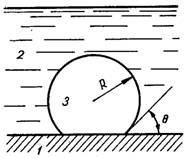
Рис.17.5. Фома парового зародка на гладкій твердій поверхні

Фізико-хімічна взаємодія трьох фаз визначається силами поверхневого натягу і величиною крайового кута θ. В умовах рівноваги це виражається співвідношенням Неймана σ₁₃ = σ₁₂ + σ₂₃cosθ чи 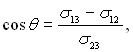де індекси 1, 2 і 3 відносяться (див. рис.17.5) відповідно до твердого тіла, рідини і газу, отже σ₂₃ = σ.

Робота утворення зародка, який виник на твердій поверхні, буде:

(17.25)

Виразивши об’єм кульового сегмента V і розміри поверхонь S₂₃ і S₁₃ в залежності від R_кр і θ, а різницю тисків в залежності від R_кр і σ, матимемо:

(17.26)

чи

(17.27)

Порівнюючи між собою рівняння (17.27) і (17.21) можна бачити, що відношення роботи утворення зародка на гладкій поверхні і в об’ємі рідини залежить від ступеня змочування рідиною твердої поверхні і є монотонною функцією величини крайового кута:

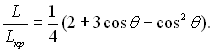(17.28)

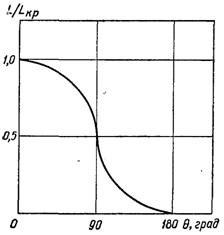
Рис.17.6. Вплив змочування твердої поверхні на роботу утворення парового зародка

Залежність L /L_кр від θ наведена на рис.17.6, з якої видно, що на не змочуваній поверхні при значеннях θ близьких до 180 °, робота утворення зародка стає дуже малою, а ймовірність його утворення наближається до одиниці. Однак цей висновок представляє тільки теоретичний інтерес, тому що для найбільш частіше у техніці сполучення рідина – тверда поверхня величини крайових кутів не перевищують 90°, а максимальне значення виміряного в дослідах кута змочування досягало 140°. У реальних умовах не буває крайових кутів близьких до 180°.

Отже, вплив змочування може привести до зменшення роботи утворення зародка на гладкій поверхні максимум у 2...3 рази. При цьому ймовірність утворення зародка залишається ще дуже малою, а необхідність перегріву рідини – високою. Це повністю відповідає установленому дослідами факту, що у посудині з дуже гладкими стінками кипіння рідини розпочинається при високому її перегріві, який значно (на десятки градусів) перевищує перегрів рідини, за якого виникає її кипіння на шорсткій поверхні.

Погане змочування гладкої горизонтальної поверхні рідиною (θ > 90°), слабко впливає на зародкоутворення і перегрів, але чинить помітний вплив на процес бульбашкового кипіння відносно його стабілізації. Якщо в довільній точці не змочуваної ділянки поверхні починається кипіння, то утворення бульбашок у цій точці буде відбуватися безперервно і стійко. Форма парових бульбашок у цьому випадку така, що після відриву бульбашки на гладкій поверхні залишається слід у вигляді крупного парового утворення, що і забезпечує високу стабільність процесу.

Висновок про слабкий вплив змочування на процес зародкоутворення в повній мірі стосується також гладких похилих і вертикальних поверхонь нагріву. Відносно впливу поганого змочування на стабільність процесу кипіння вертикальні поверхні відрізняються від горизонтальних. З виконаних теоретичних і інструментальних досліджень виходить, що у випадку вертикальної поверхні відбувається повний відрив парової бульбашки від стінки без залишку на ній сліду і локальної стабілізації процесу кипіння не спостерігається.

Реальні (технічні) поверхні нагріву ніколи не бувають абсолютно гладкими. Вони є у більшій чи меншій мірі шорсткими і характеризуються мікрорельєфом, наявністю мікроскопічних виступів і западин, геометричні розміри яких спів розмірні з розмірами парових зародків. На шорсткій поверхні створюються умови, які значно полегшують процес зародкоутворення. До них передусім відноситься наявність на таких поверхнях мікроскопічних пор. У свій час про те, які нерівності шорсткості поверхонь – виступи чи западини – є активними центрами зародкоутворення, був предметом дискусії. В останній час це питання розв’язане у тому змісті, що активними центрами кипіння можуть бути тільки мікрозаглиблення. Доказана важлива роль западин, їх погане змочування рідиною і хороше змочування газом, що веде до адсорбції газу твердою поверхнею.

Форма і розміри мікрозаглиблень (западин, капілярних пор, тріщин, канавок) на реальних поверхнях нагріву на реальних поверхнях різноманітна і ще маловивчена. Тому приходиться будувати теорію зародкоутворення на спрощеній моделі, розглядаючи при цьому найпростіші геометричні форми западин – циліндричну і конічну – і ряд спрощень при розв’язку задачі. Результати аналізу при цьому носять якісний, а не кількісний характер.

Принципову перевагу заглиблень у порівнянні з плоскою поверхнею відносно зменшення роботи зародкоутворення можна бачити з рівняння (17.25). Складова роботи L, обумовлена поверхневими силами, L′ = σ(S₂₃ + S₁₃cosθ). Звідки виходить, що чим більше відношення S₁₂/(S₂₃ + S₁₃), тим менше L′ при даних значеннях σ і θ. У заглибленнях це відношення помітно більше, ніж на плоских поверхнях, а робота  L′ відповідно менша. Але значення цієї переваги для спонтанного зародкоутворення не варто переоцінювати, особливо для змочуваних поверхонь.

Для конічних пор отримано залежність, яка дозволяє знайти відносне (у порівнянні з плоскою поверхнею) зменшення роботи зародкоутворення в них у випадку різних значень кутів φ при вершині конуса і крайових кутів змочування θ.

Розглянуто також умови росту зародків у циліндричній закритій знизу з боку твердого тіла порі і вияснено ступінь активності пори як центра газоутворення для змоченої і не змоченої рідиною поверхні. На рис.17.7,а наведені етапи розвитку газового зародку у випадку змоченої поверхні, коли меніск має ввігнуту форму, яку для капілярних форм можна вважати сферичною. Вважається, що у початковий момент І у нижній частині пори існує початковий газовий зародок з радіусом меніска більшим R_кр.

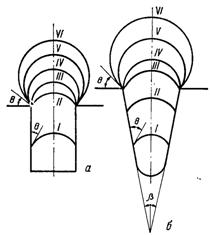
Рис.17.7. Схема росту парового зародку в циліндричній (а) і конічній (б) порах

Якісна картина проходження процесу така. Якщо радіус меніска R_м більше R_кр, то при підведенні теплоти до перенасиченої рідини буде відбуватися ріст зародка і витіснення рідини з пори. Після того як границя розділу рідина – газ досягне устя западини (ІІ), ріст зародка буде продовжуватися при зменшенні до певного мінімуму значення (ІІІ) радіуса його кривизни. У цей момент тиск у бульбашці буде максимальним. При подальшому рості бульбашки радіус його кривизни буде збільшуватися (IV…VI), а тиск у ньому падатиме. Ріст зародка у конічній порі (рис.17.7,б) полегшується, тому що він буде здійснюватися при постійному зростанні радіуса кривизни у самій порі.

У випадку не змочуваної поверхні рідиною обидві стадії процесу – витіснення рідини з пори і перехід в положення, яке визначається поверхневими силами на горизонтальній поверхні, – проходить у більш сприятливих умовах. Витіснення рідини з пори полегшується, тому що при випуклому меніску йому сприяють поверхневі сили. У той же час механічна рівновага системи зародок – рідина забезпечується при меншому тиску, ніж у випадку змочуваної поверхні. При крайових кутах θ > 90° полегшується також вихід бульбашки з пори і перехід його на горизонтальну поверхню. З цього можна зробити висновок про обмеженість активності змочуваних пор і високій активності, як центрів утворення газової (парової) фази, не змочуваних пор.

Перевага погано змочуваних пор криється також у тому, що заповнення такої пори рідиною після відриву бульбашки затруджене. У багатьох випадках при відповідному сполученні форми (круті стінки, гостре дно), геометричних розмірів пори і поверхневого натягу рідини можливість заповнення взагалі виключається. Цим забезпечується сталість існування в порі початкового зародку і стабільність її роботи як центра пароутворення.

Парові зароки виникають переважно в не змочуваних западинах, тому що в них робота утворення зародка (відриву рідини від твердої стінки) невелика. Добре змочувані западини можуть бути деякий (часто досить тривалий) час центрами пароутворення за наявності в них мікроскопічних газових утворень. При тривалому кипінні може відбуватися дегазація западин, заповнення їх рідиною і припинення їх функціонування як активних центрів. У цьому відношенні мають переваги незмочуванні западини.

Виникненню парового зародка в заглибленні на поверхні твердого тіла сприяють: газові бульбашки і інші сторонні включення – пилу, колоїдних частинок; наявність на твердій поверхні місць (забруднень), які погано змочуються рідиною (локальне незмочування западин) і добре змочуваних газом чи парою; адсорбція твердою поверхнею газових і парових молекул.

Зародок, що виник на поверхні, заповнює пору, виштовхує з неї рідину і досягає устя пори. Далі відбувається його перехід з положення, яке визначається рівноважними поверхневими силами на стінках пори, до положення, визначається силами змочування на горизонтальній поверхні.

Якщо крайовий кут θ більший половини кута розкриття западини φ, то бульбашка після утворення склепіння над устям пори повинна перевалити через положення, за якого радіус її кривизни стає мінімальним. Значення цього проміжного мінімуму R_min практично співпадає з величиною радіуса устя пори R_c. Якщо θ ≤ φ/2, то такого проміжного мінімуму радіуса кривизни не буде і ріст бульбашки при виході з пори буде відбуватися у більш сприятливих умовах. Можливість подальшого росту бульбашки в тому чи іншому випадку визначається перегрівом рідини у пристінному шарі.

17.5. Особливості поведінки паро-газових зародків

На перегрів, який відповідає виникненню кипіння, може помітно вплинути наявність у рідині розчинених газів. Умовою механічної рівноваги паро-газового зародку в об’ємі рідини у цьому випадку буде співвідношення

де р_п і р_г – парціальні тиски пари і газу всередині зародка.

У відповідності з цією умовою наявність газу в зародку приводить до зменшення необхідного парціального тиску пари і тим самим до зменшення необхідного для рівноважного існування зародка у перегрітій рідині. Доказано, що паро-газові зародки характеризуються більш складною поведінкою, ніж чисто парові. Вважаємо, що маса інертного газу, яка міститься в зародку радіусом R, становить т_г. Тоді, використовуючи співвідношення для ідеального газу

умову рівноваги зародка можна записати наступним чином:

(17.29)

Характер цієї рівноваги в ізотермічних умовах визначається знаком похідної д(р_п – р)/дR: при д(р_п – р)/дR > 0 рівновага стійка, у протилежному випадку – нестійка, за якої саме мале відхилення об’єму зародка від визначального виразу (17.29) приведе до самочинним і незворотним.

Максимальний радіус зародка, який містить необхідну кількість газу, при якій він ще зберігає стійкість, знаходиться з (17.29) за умови д(р_п – р)/дR = 0. Це значення:

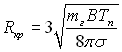(17.30)

назване критичним.

При R < R_кр рівновага паро-газового зародка буде стійкою, при R > R_кр – нестійкою. Умові R = R_кр відповідає різниця тисків пари і рідини:

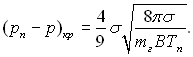(17.31)

Співвідношення між R_кр і (р_п – р) при цьому має вид:

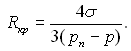(17.32)

Використовуючи рівняння Клапейрона – Клаузіуса і вважаючи, що Т_п≈Т_н, величину R_кр можна виразити через перегрів

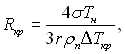(17.33)

а вираз (17.29) привести до виду:

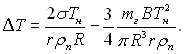(17.34)

Залежність ΔТ(R) має вигляд кривої з максимумом, при цьому у випадку, коли R > R_кр вона асимптотично наближається до залежності (17.10), яка описує нестійку рівновагу чисто парового зародку (рис.17.8).

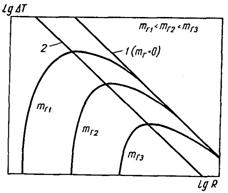
Рис.17.8. Вплив наявності газу у паро-газовому зародку на його рівновагу 1 – по (17.10); 2 – по (17.33)

Таким чином, поведінка паро-газового зародка має наступні особливості. По-перше, перегрів, який необхідний для його рівноваги (стійкої чи нестійкої), завжди менший перегріву, який необхідний для рівноваги чисто парового зародка того ж розміру. По-друге, якщо розмір рівноважного зародка R < R_кр, то зародок зберігає стійку рівновагу при збільшенні перегріву аж до значення ΔТ_кр(т_г). У цьому випадку розмір його збільшується до R_кр, після чого стійка рівновага стає неможливою – зародок починає самочинно рости при подальшому незначному підвищенні ΔТ. Отже, якщо такий зародок відповідає області під кривою ΔТ(R), то він починає конденсуватися до рівноважного розміру; якщо зародок знаходиться над цією кривою так, що ΔТ < ΔТ_кр, то він росте до рівноважного розміру. В усіх інших випадках зародок буде необмежено рости.

У цьому аналізі за незалежний параметр прийнята маса газу в зародку (т_г). При подібному розгляді (стосовно конічних западин на твердій поверхні) за такий параметр приймався парціальний тиск газу в западині до проникнення в неї рідини р_г.поч. У цьому випадку тиск газу при заповненні западини буде:

(17.35)

де h – глибина пори; х – висота паро-газового зародка у порі.

Якщо ці уявлення застосувати до паро-газового зародка в об’ємі рідини, то зміна парціального тиску газу при зміні об’єму зародка буде визначатися рівнянням:

(17.36)

У цьому рівнянні R_поч – деяке реперне значення радіусу зародка, при якому заданий початковий тиск газу.

З урахуванням (17.36) за умови д(р_п – р)/дR = 0 можна отримати

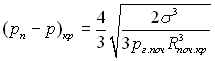(17.37)

– вираз, еквівалентний (17.31), оскільки . З нього у свою чергу слідує співвідношення:

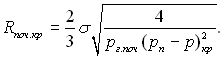(17.38)

Аналогічне рівняння отримано для западини на твердій поверхні:

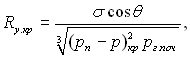(17.39)

чи, при виражені (р_п – р) через ΔТ, матимемо

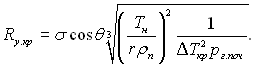(17.40)

У цих рівняннях R_у.кр – мінімальний радіус устя западини, у якій до проникнення рідини парціальний тиск газу становив р_г.поч і яка після часткового заповнення рідиною при заданому перегріві поверхні залишалася активною.

17.6. Початок кипіння на поверхні нагріву

Уявлення про існування в заглиблені готового зародку є вихідним при розгляді задач теорії бульбашкового кипіння на твердій поверхні: а) визначення умов початку кипіння і б) знаходження розмірів западин, які можуть бути активними центрами пароутворення.

Перші спроби наближеного розв’язку цих задач будувалися на основі дуже спрощеного підходу. Так, на підставі того, що зв’язок між критичним радіусом R_кр і перегрівом ΔТ визначається формулою (17.10), зроблений висновок, що западина може бути центром пароутворення, якщо радіус її устя дорівнює R_кр чи більший за нього. З цього виходить, що необхідний для початку кипіння перегрів рідини обумовлюється радіусом найбільшої не змоченої западини. Вважаючи, що єдиною характеристикою активності западини є розмір (радіус) її устя між стінками R_c, а необхідний перегрів можна визначити з формули (17.10), якщо в неї замість R_кр підставити R_c:

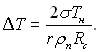(17.41)

Якщо вважати, що температуру рідини можна замінити температурою поверхні нагріву Т_с і замість ΔТ застосувати ΔТ_с = Т_с – Т_н, то формула (17.41) набуде вигляду

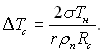(17.42)

Досліди по визначенню активності штучних западин відомих розмірів підтвердили коректність (17.42) тільки для умов рівномірного перегріву рідини і поверхні. При кипінні в реальних умовах з підводом теплоти від поверхні до рідини визначеній по (17.42) перегрів поверхні (1,7 К) значно відрізняється від його дослідного значення (11,1 К). Некоректність співвідношень (17.41) і (17.42) для реальних умов очевидна, тому що з цього виходить, що для поверхні із западинами великих розмірів перегрів, який відповідає початку кипіння, повинен бути дуже малим, що у дійсності не спостерігається.

Викладені уявлення про процес у відповідності з співвідношеннями (17.41) і (17.42) відповідають граничному випадку, коли перегрів рідини дорівнює перегріву стінки і є постійною величиною по висоті її шару. У цьому випадку наближений теоретичний аналіз приводить до висновку, що при заданому перегріві існує певне мінімальне значення R_c активної западини: усі западини меншого радіуса не можуть бути активними, а всі западини більшого радіуса будуть активними.

Особливості процесу бульбашкового кипіння на поверхні нагріву криються в тому, що він відбувається в умовах існування температурної нерівномірності. Паровий зародок, який утворив склепіння над устям западини, оточений нерівномірно перегрітою по його висоті рідиною. Тому при визначенні умов рівноваги системи зародок – рідина необхідно враховувати профіль температури рідини у пристінному шарі.

Таким умовам існування зародка присвячено ряд робіт, де розглянуто різні варіанти задачі і її наближене вирішення для різних конкретних умов.

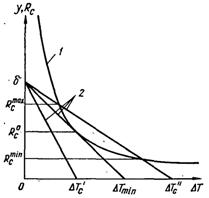
Рис.17.9. Схема розв’язку задачі про початок кипіння на поверхні нагріву

Основна ідея і загальна схема розв’язку цієї задачі у спрощеному вигляді наведена на рис.17.9. Умови задачі: рідина в основній її масі догріта до температури насичення Т_н, зародок утворив над устям западини склепіння у формі півсфери, тобто радіус устя западини дорівнює критичному радіусу зародка R_c = R_кр, а крайовий кут θ = 90°. Критичний радіус R_кр і товщина теплового пограничного шару δ – величини співрозмірні.

Якщо R_c = R_кр, то з (17.10) виходить, що

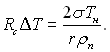(17.43)

Права частина рівняння (17.43) при заданому тиску рідини – величина стала (зміна r і ρ_п у стані нестійкої рівноваги дуже мала). Отже, зв’язок між R_c і ΔТ визначається рівнянням рівносторонньої гіперболи (крива 1).

Якщо зміну перегріву в пристінному шарі δ по висоті вважати для простоти лінійною, то цю зміну при різних перегрівах поверхні нагріву ΔТ_с можна представити сімейством прямих у = δ – тΔТ_с, проведених з точки на осі ординат, яка відповідає ΔТ_с = 0 і розташованій на висоту у = δ, до перетину з віссю абсцис у відповідній точці ΔТ (пряма 2).

При малих ΔТ_с прямі 2 і крива 1 не пересікаються і не дотикаються, але при збільшенні ΔТ_с до певного його значення ΔТ_min пряма 2 стає дотичною по відношенню до кривої 1, тобто у них з’являється спільна точка. Для подальшого розгляду необхідно ввести критерій початку росту парового зародка у нерівномірно перегрітому шарі рідини на поверхні нагріву. Можна, наприклад, прийняти, що для забезпечення росту зародка локальний перегрів рідини ΔТ , рівний необхідному ΔТ  для даного R_c = R_кр у відповідності з рівнянням (17.43), повинен мати у вершині склепіння, тобто у точці, яка знаходиться на максимальній відстані від твердої поверхні. При цьому всі інші ділянки поверхні зародка будуть знаходитися в більш сприятливих умовах, дотикаючись до більш перегрітих шарів рідини.

З рис.17.9 виходить, що загальна для обох ліній точка відтворює умову, яка відповідає змісту прийнятого критерію. Абсциса ΔТ_min визначає мінімальний перегрів рідини, за якого можливе кипіння, а ордината у = R_c⁰ – відповідає радіусу активної западини. При більш високих перегрівах поверхні ΔТ_с > ΔТ_min пряма 2 пересікає криву 1 у двох точках. Точки перетину цих ліній відповідно визначають два значення радіусів R_c^min і R_c^max, у межах яких знаходяться розміри активних западин при даному перегріві ΔТ_с > ΔТ_min.

Таким чином, прийняв ряд передумов, можна відповісти на обидва питання: а) про початок кипіння (ΔТ_min) і б) про розміри активних западин (від R_c^min до R_c^max).

Реальні умови процесу значно складніші, ніж прийняті зі спрощеннями для простоти викладення суті методу. У багатьох роботах задача розглядалася в більш близькій до реальних умов постановці, однак враховувалися не всі фактори, які впливають на процес. Ураховується можливість деформації температурного поля пристінного шару рідини біля зародка, і критерії початку кипіння формулюються у загальному виді. Вводиться поняття характерної точки неспотвореного шару на відстані h від твердої стінки і приймається, що для початку кипіння необхідна рівність перегріву рідини у цій точці і перегріву по (17.10). Приймається більш складний характер зміни температури Т=Т(у, Т_с) у тепловому пограничному шарі. Розгляд не обмежується напівсферичною формою утворення зародком склепіння. Приймається, що характерні розміри – висота зародка b, відстань від поверхні нагріву до характерної точки h, радіус западини R_c і критичний радіус зародка R_кр – зв’язані між собою лінійними співвідношеннями b = C₁R_c; R_кр = С₂R_c; b = C₃R_кр; h = C₄b, де значення коефіцієнтів C₁, C₂, C₃ і C₄ зазвичай недалекі від одиниці (найчастіше від 1 до 2). Тоді на підставі (17.10) температуру пари у зародку Т_п можна виразити у вигляді простої залежності від h:

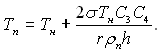(17.44)

При збільшенні температури стінки Т_с настає момент, коли температура рідини Т на відстані від стінки у = h = С₁С₄R_c стає рівною Т_п по (17.44):

(17.45)

Отже, для западини даного розміру, які характеризується радіусом устя R_c, виконується прийнята умова початку кипіння. Далі достатньо незначного підвищення температури рідини для забезпечення росту зародка до макроскопічних розмірів.

На достатньо шорстких поверхнях з широким діапазоном розмірів западин (до яких відносяться технічні поверхні нагріву) умова (17.45) виконується перед усім для западини з деяким радіусом устя R_c⁰, який можна назвати найбільш сприятливим, тому що кипіння почнеться дійсно на цій западині. При цьому матиме місце дотику кривих, які описуються лівою і правою гілкою рівняння (17.45), у точці дотику виконується умова рівності перших похідних

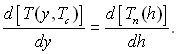(17.46)

З розв’язку системи рівнянь (17.45) і (17.46) можна отримати значення ΔТ_min – мінімального перегріву, який відповідає початку кипіння, і величину R_c⁰– радіуса устя першої западини, на якій розпочинається кипіння. Такий підхід і схему розв’язку використано для вирішення різних варіантів задачі у залежності від прийнятого профілю температури у пограничному шарі і прийнятих значеннях коефіцієнтів С₁...С₄. При цьому вважалося, що форма мікроскопічного зародку визначається значенням крайового кута θ, тобто так само, як і макроскопічної бульбашки, вирази для коефіцієнтів С₁...С₃ мають вигляд:

(17.47)

Якщо вважати, що R_c = R_min і зародок має форму півсфери, то С₁ = С₂ = С₃ = = 1. У найпростішому випадку лінійної зміни температури у шарі рідини завтовшки δ від Т_с до Т_об (де Т_об – температура в об’ємі рідини за межами шару δ) для шорсткої поверхні нагріву можна отримати такі залежності. Мінімальний перегрів поверхні нагріву ΔТ_min = (Т_с – Т_н)_min необхідний для початку кипіння при недогріві ΔТ_нед = (Т_н – Т_об):

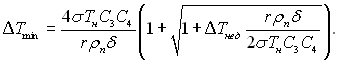(17.48)

Найбільш сприятливий радіус устя западини [ΔТ^′_min = (Т_н – Т_об)_min]

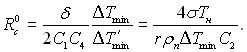(17.49)

Перегрів поверхні ΔТ_с = (Т_с – Т_н) необхідний для активації западини даного розміру становить:

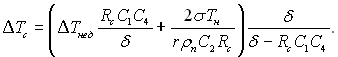(17.50)

Границі зміни радіусів устя активних западин, які відповідають перегріву поверхні нагріву ΔТ' _с = (Т_с – Т_об):

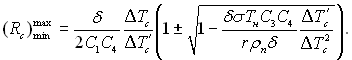(17.51)

У випадку лінійної зміни температури від Т_с до Т_об при кипінні не догрітої і насиченої рідини 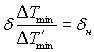і відповідно з (17.49)

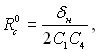(17.52)

тобто діаметр устя западини, який найсприятливіший для початку кипіння, повинен бути величиною порядку δ_н.

З рівняння (17.51) виходить, що R_c^max ні за яких перегрівах поверхні не може бути більшим δ/(С₁С₄), що не погоджується з дослідними даними, і ставить під сумнів обґрунтованість прийнятого критерію перегріву.

Запропонований інший підхід до визначення умов початку кипіння, який ґрунтується на такій пропозиції, що для рівноваги зародка достатній нульовий баланс підведеної до нього і відведеної від нього теплоти. Розглянуто випадок кипіння насиченої рідини при лінійному розподілі профілю температури у перегрітому шарі, при цьому зроблені висновки, що максимальний розмір активних западин не обмежений. На западинах R_c > δ кипіння повинно розпочатися за такого ж перегріву, як і на западинах найбільш сприятливого розміру. Для западин R_c < δ необхідний для початку кипіння перегрів визначається співвідношенням, аналогічним (17.50).

У подальшому розвинений підхід на основі уявлення про осереднену по висоті зародка температурі і розглянута задача про початок кипіння з недогрівом. Якщо для спрощення задачі прийняти рівність коефіцієнтів тепловіддачі при конденсації і випаровуванні на між фазній границі, то умова теплової рівноваги зародка буде критися у рівності температури пари у зародку і осередненої по його поверхні температурі рідини, яка оточує зародок. З урахуванням цієї умови отримані залежності для виявлення початку кипіння і розмірів активних западин. При b ≤ δ//C₄ (b = C₁R_c), де С₄ ураховує спотворення зародком профілю температур у пристінному шарі, ці залежності дуже близькі до (17.48) і (17.51), але при b > δ/C₄ отримані співвідношення, які відрізняються від (17.48) і (17.51).

Так перегрів поверхні нагріву, необхідний для початку кипіння становить:

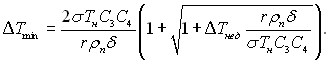(17.53)

Для максимального радіуса западини b > δ/C₄ отримано співвідношення, яке не обмежує R_c^max:

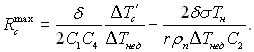(17.54)

Цей результат має принципове значення. Він дозволяє пояснити активацію штучних западин з розмірами, які відповідають b > δ/C₄. Практичне використання отриманого результату обмежене, тому що існування таких западин на реальних поверхнях малоймовірне. У той же час заповнення крупних западин рідиною дуже велика. Тому не має підстав вважати, що вони можуть бути стійкими центрами пароутворення. Наведені дослідні дані з активації штучних центрів пароутворення – западин відомих розмірів – при кипінні насичених рідин: води, етанолу і бензолу при тиску 0,1 МПа. З ряду причин (перед усім із-за невизначеності у виборі коефіцієнтів C₁, C₂, C₃ і C₄, а також товщини δ) коректне кількісне співставлення цих даних з розрахунковими затрудняється.

При представленні дослідних даних у системі координат відповідній розрахунковим співвідношенням, спостерігається велике розкидування дослідних даних. Але взагалі має місце відповідність порядку дослідних даних і розрахункових величин. Загальний якісний висновок з співставлення розрахункових і дослідних даних зводиться до того, що розміри активних западин можуть значно перевищувати межу, яка визначається рівнянням (17.51). Це свідчить про те, що підхід, який ґрунтується на тепловому балансі зародку, краще відтворює дійсну картину процесу активації западин, ніж підхід при виводі рівняння (17.51).

З відомих дослідних даних з активації природних центрів пароутворення (з початку кипіння на звичайних технічних поверхнях нагріву) виходить, що залежність (17.48) для достатньо шорсткої поверхні якісно правильно відтворює вплив основних факторів на температуру початку кипіння. Необхідний для початку кипіння перегрів поверхні збільшується з ростом недогріву і швидкості руху рідини (у зв'язку зі зменшенням δ) і зменшується зі збільшенням тиску (у зв'язку зі зменшенням відношення σТ_н/rρ_n).

Співвідношення, отримані при лінійній апроксимації профілю температури у пристінному шарі, є дуже наближеними. Кращого кількісного спів падіння розрахункових і дослідних даних можна досягти при використанні більш досконалого опису температурного профілю. Разом з цим необхідно відмітити принципову трудність (практично неможливість) отримання точного рішення задачі про початок кипіння. Причина цього криється не тільки у великій кількості допущень, які приходиться застосовувати при виводі розрахункових рівнянь. Необхідний перегрів поверхні помітним чином залежить від ступеня дегазації рідини і від стану і властивостей поверхні нагріву. Коректний облік усіх цих факторів досі неможливий.

Теоретичні рішення, побудовані на підставі уяви про готові зародки, можуть дати наближену відповідь на питання про мінімально необхідний для кипіння перегрів поверхні. Їх результати в більшій мірі відносяться не до початку кипіння, а до його припинення, тобто переходу від бульбашкового кипіння до однофазної конвекції при зменшенні температури поверхні нагріву, що супроводжується дегазацією западин.

Температура поверхні на початку кипіння може помітно відрізнятися від її температури у випадку припинення кипіння. Це пов’язано з відомим явищем гістерезису при кипінні, яке криється в тому, що температура поверхні оказується залежною від напрямку зміни режимних параметрів, перед усім – густини теплового потоку чи температурного напору. Гістерезис може проявлятися у різній ступені і може взагалі не спостерігатися. Можливість його виникнення обумовлена рядом факторів, у тому числі властивостями і станом поверхні (свіжа, така що була у вжитку) і ступенем дегазації рідини. Усе це визначає, поряд з розвитком теоретичних досліджень, доцільність виконання дослідних робіт з фіксацією початку кипіння рідин.

При кипінні насичених рідин на звичайних (достатньо шорстких) технічних поверхнях необхідні перегріви поверхні нагріву невеликі. Зазвичай вони виявляються внаслідок досліджень приблизно по кривим залежності густини теплового потоку чи коефіцієнта тепловіддачі від температурного напору, чи залежності коефіцієнта тепловіддачі від густини теплового потоку. Так, наприклад, при тиску 0,1 МПа орієнтовними значеннями ΔТ_min за умови вільного руху становить для води, метану, етану і етилену 4...8 К, для бензолу і етанолу 8...15 К.

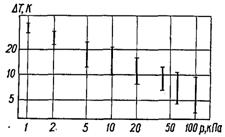
Рис.17.10. Вплив тиску на інтервал температурних напорів на поверхнях з різних матеріалів

На рис.17.10 наведені дослідні дані з температурних напорів початку кипіння води в області низьких тисків (1...100 кПа) на поверхнях нагріву, виконаних з різних матеріалів (міді, нікелю, нержавіючої сталі).

У значно ширших межах ΔТ_min змінюється при кипінні рідини з недогрівом в умовах вимушеного руху у відповідності з діапазоном зміни недогріву рідини і швидкості її руху. У дослідах зазвичай фіксують не ΔТ_min, а густину теплового потоку q_нк, яка відповідає початку кипіння, і результати дослідів подають у вигляді залежності q_нк від визначальних факторів.

Для ілюстрації впливу основних факторів на q_нк при кипінні не догрітої рідини на рис.17.11 і 17.12 наводяться результати дослідів з початку кипіння не догрітої води при малих швидкостях її вимушеного руху, тобто в умовах, близьких до умов вільного руху. Робочим елементом була горизонтальна пластина з нержавіючої сталі розміром 55×2,2×0,25. Конструкція дослідної установки забезпечувала можливість візуального спостереження. За q_нк приймалось теплове навантаження, при якому виникав перший стабільний центр пароутворення. Момент початку кипіння візуально фіксувався дуже чітко і однозначно.

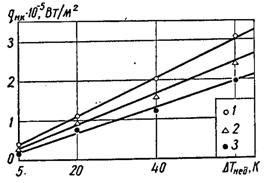
↑Рис.17.11. Вплив недогріву на початок кипінні води: 1 – р = 0,1 МПа,w = 0,2 м/с; 2 – р = 0,4 МПа,w = 0,2 м/с; 3 – р = 0,4 МПа,w = 0,1 м/с

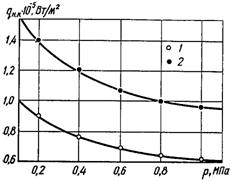
Рис.17.12. Вплив недогріву на початок кипінні води: 1 – ΔТ_нед = 20 К, w = 0,1 м/с; 2 – ΔТ_нед = 40 К, w = 0,1 м/с ↑

З рис.17.11 видно, що q_нк при даному тиску р і швидкості w практично лінійно залежить від недогріву ΔТ_нед, при збільшенні ΔТ_нед значення q_нк збільшується. Вплив швидкості руху w на величину q_нк аналогічний впливу ΔТ_нед: зі збільшенням w збільшується q_нк. На рис.17.12 наводиться вплив тиску на q_нк. Зі збільшенням р від 0,2 до 1,0 МПа значення q_нк зменшується, при цьому з ростом р темп зміни q_нк зменшується і крива q_нк = q_нк(р) асимптотично наближається до горизонталі. Характер отриманих залежностей якісно відповідає теоретичним уявленням про процес.

Величина q_нк суттєво залежить від кількості розчинених у рідині газів, а також від властивостей і стану матеріалу поверхні нагріву.

Кількість дослідів з початку кипіння в умовах вільного руху дуже обмежена. Більшість робіт виконано з виявлення початку кипіння недогрітих рідин при великих швидкостях їх вимушеного руху в трубах і каналах. У результаті цих робіт накопичений великий дослідний матеріал і запропонований ряд емпіричних і напівемпіричних співвідношень для визначення величини q_нк, основаних на різних підходах і уявленнях про процес переходу до бульбашкового кипіння. Ці співвідношення задовільно узагальнюють дослідні дані, але не стосуються інших рідин крім води.

Більш загальний підхід до розв’язку цієї задачі з більш досконалим урахуванням профілю температур у пристінному шарі в умовах вимушеного руху, запропоновано внаслідок наближеного аналітичного рішення, у наступному виді:

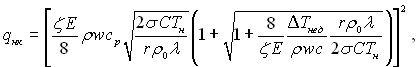(17.55)

де 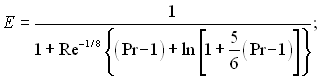Pr визначається при Т_ср = 0,5(Т_н – Т_об); ζ – коефіцієнт гідравлічного опору; Re розраховується за Т_н; С = 1 + cosθ.

Виконане опрацювання дослідних даних для води, етиленгліколю, етанолу і бутанолу показало, що формула (17.55) задовільно узагальнює дослідні дані.

Загальний висновок з наведених вище варіантів теоретичного аналізу питання про активацію западин можна сформулювати наступним чином. Обидва підходи до вирішення задачі – і уявлення про деяку характерну точку, в якій необхідна рівність відповідних перегрівів, і концепція теплового балансу зародка – до певної міри справедливі, але дуже наближені. Рішення, які виходять на підставі цих підходів, носять в більшій мірі якісний, ніж кількісний характер. Вони дають правильну якісну відповідь на питання про вплив основних факторів на початок кипіння рідин. Кількісні співвідношення, які визначають діапазон розмірів активних западин (жорстке обмеження R_c^max при першому підході і повне знаття обмежень при другому), не відповідають реальній картині процесу. Дійсні R_c^max будуть більшими за R_c^max, які передбачаються першим підходом, але будуть знаходитися в певному обмеженому інтервалі. Але основний і правильний висновок теорії криється в тому, що активними центрами пароутворення при заданих умовах можуть бути тільки западини з розмірами, які визначаються певним інтервалом R_c^min...R_c^max.