Розділ 18. РІСТ ПАРОВИХ БУЛЬБАШОК

18.1. Динаміка бульбашок, які ростуть в об’ємі рідини

Вихідна задача динаміки росту парових бульбашок криється у визначенні швидкості росту одиничної бульбашки в необмеженому об’ємі рівномірно перегрітої рідини. Спонтанно виниклий сферичний паровий зародок, радіус якого R_кр, знаходиться в стані нестійкої рівноваги з оточуючою його рідиною, і достатньо дуже малого стимулюючого подразнення, щоб зародок розпочав свій ріст до макроскопічних розмірів. Умови для таких подразнень у перегрітій рідині є.

Вирішення цієї важливої задачі посвячено немало робіт, і в останніх з них дається достатньо чіткий аналітичний опис. Задача про ріст парової бульбашки у її строгій постановці представляє собою складну спряжену динамічну і теплову задачу. Перед тим як перейти до її викладу в загальній постановці, доцільно показати динамічний і тепловий аспекти цієї задачі в ізольованому виді.

Оскільки в основі загальних рішень задачі про ріст парової бульбашки лежить рівняння Релея, яке відображає динамічний бік задачі, на ньому варто зупинитися, розглянувши більш просту, ніж динаміка росту парової бульбашки, задачу про швидкість росту в рідині газової бульбашки. Метод її розв’язку дає Релей. Задача зводиться до наступного: в необмеженій масі гомогенної нестисливої рідини, на яку не діють будь-які сили, і таку що знаходиться в стані спокою, раптово змінюється частина рідини, у ній утворюється сферичний простір; необхідно знайти миттєву зміну тиску у довільній точці маси і час, на протязі якого порожнина заповнюється; тиск на безмежності залишається сталим.

Тому що рідина нестислива, умови руху в усій її масі визначаються умовами на границі розділу рідина – порожнина. Якщо W швидкість і R – радіус границі у час τ, а w – швидкість у той же час на певній відстані ℓ (більшій за R) від центру, то при відсутності перенесення маси через границю розділу фаз W/w = R²/ℓ2 і, якщо ρ  – густина рідини, то кінетична енергія рідини буде

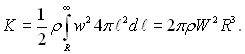(18.1)

Написавши далі вираз для виконаної роботи, і прирівнявши роботу кінетичної енергії, виразивши швидкість переміщення границі у залежності від радіусу, Релей отримав рішення задачі, тобто визначив час заповнення порожнини і тиски у різних точках простору, який зайнятий рідиною.

Виключно простий і наглядний метод Релея дозволяє легко отримати вираз для швидкості росту газової бульбашки у рідині. Нехай різниця тисків на між фазній границі і на досить великій відстані від бульбашки становить Δр. Якщо в момент часу τ радіус бульбашки R і швидкість її росту (швидкість переміщення границі розділу) W, то кінетична енергія рідини у відповідності з (18.1) К = 2πρW²R³. У наступний момент часу, який відрізняється від попереднього на нескінченно малу величину dτ, радіус бульбашки становитиме R + dR, а швидкість рідини отримає прирощення dW, тому що робота розширення бульбашки буде реалізована у вигляді прирощення кінетичної енергії рідини. У момент часу τ + dτ кінетична енергія рідини у відповідності з (18.1) становитиме:

Нехтуючи членами, які містять у собі нескінченно малі величини другого і третього порядків, отримаємо наступний вираз для прирощення кінетичної енергії:

Елементарна робота, яка здійснюється за час dτ, буде dL=4πρR²Δp. Умова dK=dL приводить до рівності

яка може бути записана в наступній формі

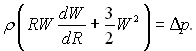
Беручи до уваги, що можна представити попереднє рівняння в кінцевому виді:

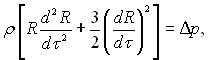(18.2)

чи у скороченій формі запису

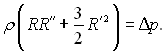(18.3)

Це диференціальне рівняння росту газової бульбашки і є рівнянням Релея.

Рівняння (18.3) можна також отримати формальним шляхом при сумісному розв’язку рівнянь руху і нерозривності потоку для сферично симетричної нестисливої рідини:

(18.4)

(18.5)

В’язкісний член 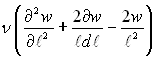у правій частині (18.4) випущений, тому що він за умови (18.5) перетворюється в нуль. Підстановка (18.5) в (18.4) з послідуючим інтегруванням по ℓ від ℓ = R до ∞  дає рівняння (18.3).

За умови, що Δр = const і R = 0 при  τ  = 0 з (18.3) виходить, що

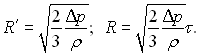(18.6) і (18.7)

Стосовно парових бульбашок співвідношення (18.7) відноситься до періоду росту, коли тиск пари у бульбашці можна вважати рівним тиску насичення при температурі перегрітої рідини Т = Т_н + ΔТ.

Розв’язок чисто динамічної задачі (без урахування поверхневого натягу і обумовленої в’язкістю рідини нормальною складовою напруги на границі розділу фаз) дає відповідь на питання про швидкість росту парової бульбашки у тому граничному випадку, коли можна вважати, що ця швидкість визначається тільки силами інерції, які виникають при розширенні бульбашки.

Другий підхід до розв’язку задачі про швидкість росту бульбашки зводиться до того, що, відхиляючись від динамічного аспекту задачі, дати наближене вирішення задачі, розглядаючи її у найпростішій постановці як чисто теплову. Він ґрунтується на використанні рівняння теплового балансу на границі розділу фаз. Через міжфазну границю за час dτ  передається деяка кількість теплоти dQ. За той же проміжок часу відбувається ріст бульбашки, її об’єм збільшується на dV_п і утворюється додаткова кількість пари dG_п. Величина rdG_п (r – теплота пароутворення) прирівнюється до dQ. Рівняння теплового балансу можна записати у такій формі:

(18.8)

де R – радіус бульбашки в момент часу τ; α  – коефіцієнт тепловіддачі, віднесений до різниці температур ΔТ =Т – Т_н.

З рівняння (18.8) виходить, що

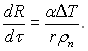(18.9)

Цим дуже простим рівнянням, на жаль, практично не можна користуватися. Воно містить у правій частині величину α, яка залежить від умов процесу, і є змінною величиною, яку необхідно визначати.

Однак описаний підхід і рівняння (18.8) дали поштовх для подальшого розгляду задачі як чисто теплової. Було запропоновано виразити густину теплового потоку на між фазній границі у такій формі

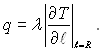
У цьому разі рівняння теплового балансу (18.8) набуває наступного виду:

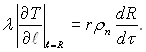(18.10)

У подальшому, для отримання рішення хоч би у грубому наближенні, можна знехтувати впливом великої кривизни міжфазної границі, використавши рішення для пластини:

(18.11)

і тоді з (18.10) можна отримати такий вираз:

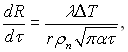(18.12)

з якого виходить, що

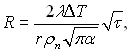(18.13)

чи, якщо виразити R через число Якоба Ja = cΔTρ/(rρ_n), то

(18.14)

Не дивлячись на наближений характер рішення, рівняння (18.14) правильно відображає вплив основних факторів на ріст бульбашки. За своєю структурою воно повністю співпадає з рядом отриманих пізніше рішень, відрізняються від них значенням постійного числового коефіцієнта.

Рішення чисто теплової задачі (без урахування гідродинамічних факторів, впливу в’язкості і поверхневих ефектів) відноситься до того граничного випадку, коли можна вважати, що швидкість росту бульбашки повністю визначається підводом теплоти до зростаючої бульбашки шляхом теплопровідності.

Стосовно до росту парової бульбашки динамічна сторона задачі може бути сформульована більш повно, якщо до правої частини рівняння Релея (18.3) замість постійної різниці тиску ввести змінну величину Δр з урахуванням додаткових ефектів, які проявляються на границі розділу фаз. У рівнянні (18.3) Δр = р – р_∞, де р – тиск рідини на між фазній границі; р_∞ – тиск на віддаленні від бульбашки. Тиск пари у бульбашці більший за тиск рідини на між фазній границі на величину

(18.15)

Перший член правої частини (18.15) обумовлений поверхневим натягом, другий – відображає вплив ефекту, обумовленого в’язкістю рідини, який проявляється на між фазній границі. Якщо у рівняння (18.3) ввести Δр з урахуванням (18.15), то рівняння Релея набуде вигляду:

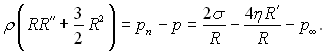(18.16)

У такому виді рівняння (18.16), яке установлює зв’язок між змінними R, р_п і τ, часто використовується як вихідне рівняння при вирішенні задачі про ріст парової бульбашки.

Більш повне формулювання теплової сторони задачі зводиться до запису енергії для рідини і граничних умов. Рівняння енергії для сферичної симетричної задачі має вид:

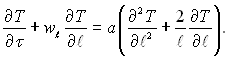(18.17)

При відсутності масопереносу на міжфазній границі чи у випадку ρ_п<< ρ радіальна швидкість рідини біля границі розділу фаз визначається з рівняння w_l = R'(R')². У загальному випадку з урахуванням масовіддачі, яка обумовлена випаровуванням рідини, 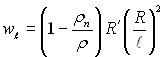чи, якщо позначити 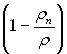через ξ , то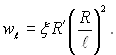

Гранична умова на міжфазній границі формулюється на основі закону збереження енергії. Теплота, що підводиться шляхом теплопровідності 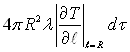і з ентальпією рідини витрачається на здійснення роботи розширення p_ndV і збільшення внутрішньої енергії пари d(u_nρ_nV):

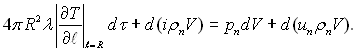(18.18)

Граничну умову часто спрощують, нехтуючи зміною одних чи інших величин. Якщо враховувати тільки зміну повної ентальпії пари внаслідок випаровування рідини, то ця умова набуває наведеного раніше виду (18.10). Оскільки точний розв’язок дуже складного рівняння (18.18) важкий, то його чи спрощують, вводячи додаткові спрощення, чи застосовують різні способи його наближеного вирішення.

Одним з перших наближених рішень задачі про ріст парової бульбашки було виконано Плесетом і Цвіком. У нашому викладі обмежимося короткою характеристикою вихідних рівнянь і отриманих результатів. Рівняння руху границі бульбашки (рівняння Релея) записується для нев’язкої нестисливої рідини у формі (18.16) без члена в правій частині 4ηR'/R, який відображає вплив в’язкості. Вводиться до розгляду початковий радіус бульбашки, для якого записується співвідношення 2σ/R_кр = р_п(Т_∞) – р_∞, де Т_∞ – температура перегрітої рідини на віддалі від бульбашки. Тоді рівняння руху можна записати так:

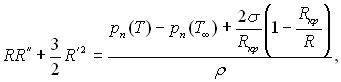(18.19)

де Т – температура на міжфазній границі.

Для знаходження температури Т використовується спрощене рівняння (18.17), і задача про переміщення границі розв’язується за умови, що зменшення температури від Т_∞ до Т відбувається в безмежно тонкому оточуючому бульбашку шарі рідини, товщина якого мала у порівнянні з радіусом бульбашки.

Наближений вираз для Т отримано у такому виді:

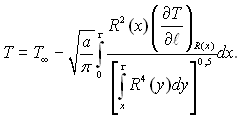(18.20)

Таким чином, задача росту парової бульбашки визначається рівнянням (18.19) і (18.20), оскільки Т і р_п(Т) виражаються в залежності від R і R'. Після певних математичних перетворень отримано наближений розв’язок задачі і прокоментовано його як для початкової стадії росту, так і для росту бульбашки при R >>R_кр. Основний член виразу для R' має вид:

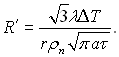(18.21)

Отже

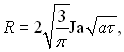(18.22)

тобто результат відрізняється від (18.14) множником 3^0,5.

Наближений розв’язок цієї задачі іншим шляхом виконали Фостер і Зубер. Рівняння Релея записується також для ідеальної рідини. Змінна різниця тисків Δр = р_п – р_∞  виражається наближено через різницю температур ΔТ за допомогою рівняння Клапейрона-Клаузіуса. Рівняння руху записується так:

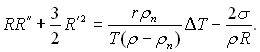(18.23)

Різниця температур ΔТ визначається розв’язком задачі теплопровідності за умови рухомої границі розділу фаз (поверхні випаровування). Рідина і парова бульбашка розглядаються як система з розподіленими по сфері тепловими стоками змінної (залежної від радіуса) потужності. На підставі цього уявлення для знаходження поля температур використовується функція Гріна для сфери і після підстановки її в (18.23) отримуємо інтегрально-диференціальне рівняння, яке описує ріст бульбашки. Оскільки розв’язок цього складного рівняння в загальному вигляді представляє практично нездоланні труднощі, то розглядаються фізично обґрунтовані міркування, які дозволяють спростити підінтегральний вираз. Що уможливлює довести наближене рішення до кінця і отримати результати розрахунків, які відповідають дослідним даним. Залежність R(τ) набуває наступного виду:

(18.24)

Отриманий результат відрізняється від (18.14) множником π/2.

Під час росту бульбашки можна виділити три стадії. Перші дві – початкова і проміжна – проходять на протязі дуже короткого проміжку часу в межах мікросекунд. Третя стадія є основною за часом і значенням. Це практично вся видима стадія розвитку бульбашки, яка називається асимптотичною. Вона характеризується тим, що швидкість росту бульбашки у цей період визначається практично повністю умовами підведення теплоти до зростаючої бульбашки. На початковій і проміжній стадіях відчувається вплив поверхневого натягу, інерції і в’язкості рідини.

Для вирішення задачі росту бульбашки для перших двох стадій наводяться оціночні дані, для третьої – конкретні наближені рішення. Так відмічається, що ріст бульбашки на початкових стадіях відбувається повільно, далі, по мірі ослаблення впливу поверхневого натягу, швидкість росту швидко збільшується доти, поки не стане суттєвим ефект охолодження. Після цього в асимптотичній стадії швидкість росту безперервно зменшується. Гідродинамічні ефекти можуть помітно впливати на ріст бульбашки тільки на початковій стадії, коли z = R/R_кр знаходиться біля одиниці. У межах мікросекунд зі збільшенням z члени рівняння, які містять гідродинамічні величини, гублять свій зміст. З оцінок виходить також, що навіть у початковий період росту нехтування гідродинамічними факторами не приводить до парадоксального висновку про великі початкові швидкості росту бульбашки. Її ріст, починаючи з критичного розміру, відбувається досить повільно в середньому пропорційно приблизно τ^3/2. Усі наведені вище співвідношення стосуються асимптотичної стадії росту.

Скрайвен отримав розв’язок задачі тільки для цієї стадії. Тому у рівнянні Релея випущені всі члени, які описують вплив поверхневого натягу, інерційності і в’язкості рідини. Це приводить до простого співвідношення р_п=р_∞ чи при рівноважному процесі випаровування – до Т_R = Т_н, що значно спрощує задачу. Але у рівняння енергії для рідини вводиться суттєве уточнення, яке враховує перенесення маси на міжфазній границі, і це рівняння набуває наступного виду:

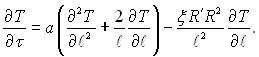(18.25)

Далі формулюються граничні і (неповністю строго) початкові умови і виконується інтегрування. Кінцевий результат зводиться до представлення виразу для R(τ) у такому виді:

(18.26)

де β – неявна функція числа Ja і відношення густин пари і рідини. Показано, що для стану не дуже близькому до критичного, і при великих значеннях числа Ja сталу росту бульбашки можна наближено приймати 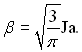При цьому рівняння (18.26) співпадає з рівнянням (18.22).

В роботах Д.О.Лабунцова показано, що отримані результати з похибкою до 2% апроксимуються виразом, в якому, крім сталих величин і (аτ)^0,5, входить тільки число Якоба Ja:

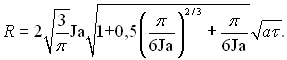(18.27)

З (18.27) видно, що при Ja >>1, тобто для області низьких і помірних тисків 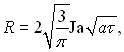а при Ja <<1, тобто при високих тисках,

У коротко викладених наближених методах вважалося, що процес випаровування відбувається рівноважно. При повному аналітичному описі задачі в її принциповій постановці повинна бути відтворена нерівноважність цього процесу незалежно від ступеня її впливу на кінцевий результат. Такий достатньо повний аналітичний опис задачі росту бульбашки у вигляді диференціального рівняння, в якому окремі члени відображають вплив визначальних параметрів на процес росту бульбашки:

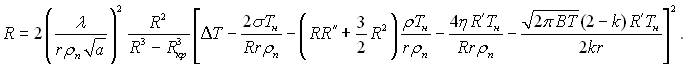(18.28)

У цьому рівнянні В – газова стала; k – коефіцієнт випаровування, рівний відношенню числа молекул, які покидають рідину і тих що залишилися в паровій фазі, до загальної кількості молекул, які підійшли до міжфазної поверхні з надлишковою складовою швидкості.

Члени правої частини рівняння (18.28), які знаходяться в квадратних дужках, характеризують вплив на швидкість росту бульбашки відповідно перегріву рідини, поверхневого натягу, інерції рідини, її в’язкості і нерівно важності процесу випаровування. Як видно з (18.28), єдиним фактором, який сприяє росту бульбашки (рушійною силою процесу), є перший доданок – перегрів рідини, який підводу теплоти до міжфазної границі і випаровування рідини. Усі інші фактори чинять опір росту бульбашки, являються “силами опору”, які зменшують швидкість її росту. Ступінь впливу окремих факторів різна на різних стадіях росту бульбашки і залежить від фізичних властивостей рідини.

У загальних рисах картина протікання процесу росту бульбашки і відносного впливу на нього різних факторів з урахуванням наведених раніше може бути представлена в такому виді. Паровий зародок, радіус якого становить R_кр, починає рости з того моменту, коли він виведений зі стану нестійкої рівноваги з рідиною, і спочатку росте дуже повільно внаслідок суттєвого впливу всіх гальмівних факторів, особливо поверхневого натягу. Тривалість цього періоду дуже мала. Вона визначається головним чином величиною перегріву рідини ΔТ і масштабом початкового подразнення.

Далі дуже швидко вплив поверхневого натягу і в’язкості зменшується до дуже малої , у порівнянні з впливом перегріву рідини і її інерції, величини, швидкість росту бульбашки швидко збільшується і прискорення досягає максимуму. У цей період відбувається швидке падіння температури у бульбашці на між фазній границі, обумовлене охолоджувальним ефектом випаровування рідини.

При досягненні максимуму прискорення у зв'язку зі сповільненням росту бульбашки зменшується вплив сил інерції. У подальшому при сповільненому рості вплив їх зменшується на стільки, що ріст бульбашки (при дуже малій ролі ефекту нерівноважності) починає обмежуватися практично тільки умовами підведення теплоти.

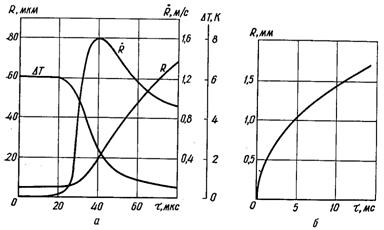
Рис.18.1.Початкова (а) і асимптотична (б) стадії росту парової бульбашки

Таким чином, процес переходить в основну за протяжністю асимптотичну стадію. Тривалість стадій, які передують асимптотичній, зазвичай дуже мала. На рис.18.1 наведено, отримані теоретичним шляхом, хід кривих зміни R, а також хід кривих зміни R' і Т на початкових стадіях росту бульбашки.

Можна визначити швидкість росту бульбашки, викликану любим фактором, нехтуючи впливом інших. Дійсна швидкість росту буде меншою за найменшу з величин, визначених таким чином, чи у граничному випадку практично дорівнює цій величині, якщо вплив інших факторів дуже малий.

Найменш помітну роль у сумі опорів росту бульбашки відіграють два останніх доданка у квадратних дужках рівняння (18.28), які відображають вплив в’язкості рідини і нерівно важності процесу випаровування. Обумовлений в’язкістю рідини ефект проявляється границі розділу фаз у вигляді нормальної складової тензора в’язких напруг. Якщо представити собі у граничному випадку ситуацію, в якій можна знехтувати впливом усіх інших факторів, то швидкість росту бульбашки у цьому випадку, у відповідності з (18.15), визначається співвідношенням

(18.29)

Вплив цього фактору незначний. Він може помітно проявлятися при малих розмірах зростаючої бульбашки і при високій в’язкості рідини.

Нерівно важність процесу випаровування викликає стрибок температур на між фазній границі (T_R > T_n). Урахування цього фактору не підставі модекулярно-кінетичної уяви для швидкості росту бульбашки у тому випадку, коли визначальними є тільки модекулярно-кінетичні закономірності, приводить до залежності:

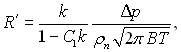(18.30)

де С₁ = 0,399 ≈ 0,4.

Формула (18.30) містить у собі коефіцієнт випаровування k – величину недостатньо вивчену, значення якої знаходиться в дуже широких межах. Зазвичай k оцінюють як величину близьку до одиниці. Загальний висновок з наведених рішень криється у тому, що нерівно важність процесу випаровування відіграє помітну роль тільки при досить малих значеннях k, тоді як при k близьких до одиниці, вплив цього фактору на швидкість росту бульбашки дуже малий.

На асимптотичній стадії росту макроскопічної бульбашки швидкість її росту практично повністю визначається підводом теплоти до бульбашки. Рівняння росту бульбашки від R_кр до R у випадку нехтування впливом усіх гальмівних факторів витікає з загального рівняння (18.28):

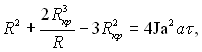(18.31)

що при R >> R_кр приводить до виразу R = 2Ja(aτ)^0,5.

Рівняння росту бульбашки, яке описує з достатньою точністю і до асимптотичну стадію має вигляд:

(18.32)

де

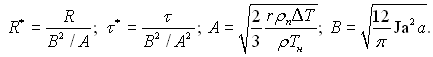
Рівняння (18.32) при τ* >> 1 набуває вигляд, аналогічний раніше наведеним рівнянням для асимптотичної стадії росту. Співставлення дослідних даних з росту бульбашок з розрахунковими даними, отриманими по рівняннях (18.22), (18.24), (18.27) і (18.32), наведено на рис.18.2. Як видно з цього рисунку, рішення, запропоновані для асимптотичної стадії (18.22), (18.24) і (18.27), при τ* ≥ 10 дає задовільне погодження з дослідними даними результати. Розрахункові величини, отримані за цими рівняннями, помітно відхиляються від дослідних значень при τ* < 10. Відхилення дослідних даних від розрахункових за рівнянням (18.32) відбувається тільки на дуже ранній стадії росту при τ* < 10^–3.

Розгляд рівнянь, які описують ріст бульбашки, і отримані на їх основі рішення дозволяють зробити висновок про достатню повноту і правильність сучасних уявлень про процес росту парової бульбашки в перегрітій рідині.

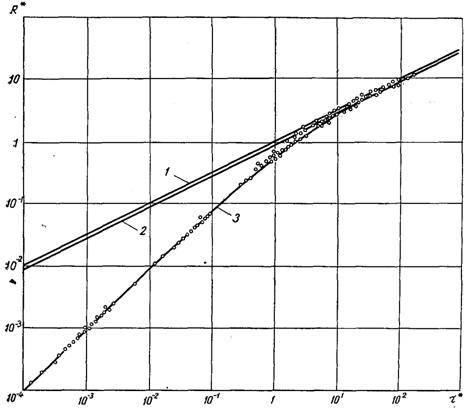
Рис.18.2. Порівняння дослідних даних з росту бульбашок в об’ємі перегрітої води (р = 1...40 кПа, ∆Т = 4...20 К) з розрахунком: 1 – по (18.22), (18.27); 2 – по (18.24); 3 – по (18.32)